Modelo electrodébil
El modelo electrodébil es una teoría física que unifica la interacción débil y el electromagnetismo, dos de las cuatro fuerzas fundamentales de la naturaleza.
El modelo electrodébil fue desarrollado en la década de 1960 por Sheldon Lee Glashow, Abdus Salam y Steven Weinberg.
La constatación experimental de las interacciones nucleares débiles mediadas por corrientes cargadas (
Estos tres investigadores recibieron el Premio Nobel de Física en 1979.
Presumiblemente, el modelo electrodébil es un caso límite de una Teoría de Gran Unificación (GUT), que uniría la interacción electrodébil con la interacción fuerte.
Esa teoría era un tanto fenomenológica y era sólo válida para bajas energías y una cantidad limitada de procesos débiles.
La teoría original de Fermi llevaba a nudos cuádruples dentro de los diagramas de Feynman, que eran en realidad "diagramas colapsados", eliminando lo que en la teoría electrodébil moderna eran las líneas para los bosones intermedios.
Es decir, la teoría moderna implica que los cálculos perturbativos mediante diagramas de Feymann, tengan sólo nudos triples, donde se unen una línea bosónica con dos fermiónicas.
Si se suprimen las líneas bosónicas de los bosones intermediarios W y Z entre nudos triples, resulta un nudo cuádruple donde convergen cuatro líneas fermiónicas, que es el diagrama típico de la teoría de Fermi.
Si bien la teoría teoría original de Fermi, tenía ciertos éxitos y predictividad, teneía otros problemas: no tenía la estructura de teoría gauge renormalizable, por lo que sólo podía proporcionar aproximaciones bastante limitadas.
Es decir, en esa teoría los fermiones son descritos mediante un lagrangiano de Dirac generalizado adecuadamente para que sea invariante gauge bajo un cierto grupo gauge de simetría interna.
En la formulación del Modelo Estándar (SM) no existe a priori una elección única de la simetría del lagrangiano de las interacciones electrodébiles.
Así, las corrientes cargadas de Yang-Mills incluyen solamente fermiones levógiros y no se conocen neutrinos dextrógiros.
Es por ello que los campos fermiónicos levógiros son agrupados en dobletes, mientras que los campos dextrógiros son singletes del grupo
es la "quinta" matriz de Dirac que se transforma como un pseudoescalar.
En la representación anterior no se puede (a menos que se rompa explícitamente la simetría gauge) introducir un término de masa en la lagrangiana que describe la cinemática de los fermiones.
Por todo ello, el grupo de gauge mínimo que describe las interacciones electrodébiles es
está asociada a la conservación del isospín débil,
introduce de manera natural cuatro campos bosónicos sin masa:
Sin embargo el hecho experimental de que las interacciones débiles actúan solo a distancias extremadamente pequeñas, era un indicador claro de que los bosones transmisores de la fuerza débil debían poseer masa, como fue demostrado posteriormente.
rompería explícitamente la simetría gauge, haciendo la teoría no renormalizable.
El proceso por el cual se consigue introducir los términos de masa en el modelo se denomina ruptura espontánea de simetría electrodébil.
En esa forma el modelo sólo es aplicable a muy altas energías cuando los bosones intermediarios W y Z no tienen masa.
Para entender como es lagrangiano efectivo en las condiciones normales de nuestro universo debemos añadir ciertos términos al lagrangiano de la sección anterior.
Con el objetivo de mantener la invariancia de gauge, las derivadas del campo que intervendrán en el lagrangiano se toman como derivadas covariantes:
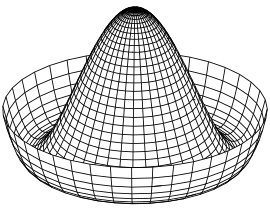
es el valor esperado del campo de Higgs en el vacío, que al ser no nulo produce el potencial de "sombrero mexicano" mostado en la figura, que tiene una inestabilidad cuando el campo es nulo, lo cual lleva a la ruptura espontánea de la simetría.
Si consideramos ahora que la forma de campo se puede escribir como:
Escribimos el sector de Higgs del lagragiano que interacciona con los bosones electrodébiles como:
Y entonces la contribución del sector de Higgs fenomenológicamente es equivalente a que tres de los campos bosónicos intermediarios tuvieran masa:
que representará el potencial electromagnético del fotón se ve afectado por términos de masa, por lo que los fotones en esta teoría se comportarían como partículas sin masa.