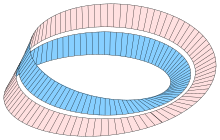
Gorra cruzada
En matemáticas, una gorra cruzada[1] (nombre original en inglés: "cross-cap")[2] es una superficie bidimensional en el espacio tridimensional que es unilateral, y que además se corresponde con la imagen continua de una banda de Möbius que se cruza en un intervalo.
En el punto donde el intervalo más largo se dobla por la mitad en la imagen, la configuración cercana es la del paraguas de Whitney.
El borde delimitador de una gorra cruzada es un lazo cerrado simple.
Una gorra cruzada que se ha cerrado pegando un disco a su límite es un modelo del plano proyectivo real P2 (de nuevo con un intervalo de auto-intersección, y dos puntos donde este modelo no es una inmersión de P2).
Un importante teorema de topología, el teorema de clasificación para las superficies, establece que cada variedad bidimensional compacta sin límite es homeomorfa a una esfera con un número (posiblemente 0) de "asas" y 0, 1, o 2 gorras cruzadas.