Integral exponencial

En el ámbito de las matemáticas la integral exponencial es una función especial definida en el plano complejo e identificada con el símbolo  Ei.

se define como Esta definición puede ser utilizada para valores positivos de

, pero a causa de la singularidad del integrando en cero, la integral debe ser interpretada en término del valor principal de Cauchy.

Para valores complejos del argumento, esta definición es ambigua a causa de los puntos de ramificación en 0 y en

[1]​ En general, se realiza un corte en el eje real negativo y Ei puede ser definida mediante una continuación analítica en el resto del plano complejo.

Se utiliza la siguiente notación,[2]​ Para valores positivos de la parte real de

, esto se puede expresar como[3]​ El comportamiento de E1 cerca del branch cut puede ser analizado mediante la siguiente relación:[4]​ Las propiedades de la exponencial integral mostradas, en ocasiones, permiten sortear la evaluación explícita de la función a partir de la definición dada arriba.

, y extraer la singularidad logarítmica, se puede obtener la siguiente representación en forma de serie de

real:[5]​ Para argumentos complejos fuera del eje real, esta serie se generaliza a[6]​ donde

complejo, y tomamos el valor usual del logaritmo complejo con el corte de rama a lo largo del eje real negativo.

Por desgracia, la convergencia de las series mostradas arriba es muy lenta para argumentos con gran módulo.

, se necesitan más de 40 términos para obtener una respuesta correcta con 3 cifras significativas.

[7]​ Sin embargo, existe una serie asintótica divergente que puede ser obtenida a partir de la integración de

por partes:[8]​ cuyo error es del orden

y es válida para grandes valores de

De las series dadas arriba, se deduce que

se comporta como una exponencial negativa para grandes valores del argumento y como un logaritmo para pequeños valores del mismo.

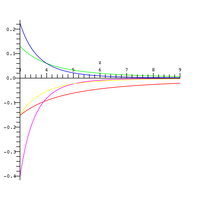
Para valores reales positivos del argumento,

queda acotada superior e inferiormente por funciones elementales como sigue:[9]​ La parte izquierda de la desigualdad se muestra en la gráfica de la izquierda en azul, la parte central, que es

pueden ser escritas de forma más simple mediante la función entera

Se sigue inmediatamente que: La integral exponencial está altamente relacionada con la función logaritmo integral

por la siguiente relación para valores positivos reales de

La integral exponencial se puede generalizar a que es una familia de funciones que puede representarse como un caso especial de la función gamma incompleta:[11]​ Esta forma generizada se llama a veces función de Misra function[12]​

, que se define como Las derivadas de las funciones

pueden ser obtenerse mediante el uso de la fórmula[13]​ Nótese que la función

es sencilla de evaluar (dando un término inicial a la relación recursiva), pues es

es imaginario, la función tiene una parte real no nula, así podemos usar la fórmula para obtener una relación de la exponencial integral con las integrales trigonométricas

: Las partes real e imaginaria de

están dibujadas en la gráfica de la derecha en negro y rojo respectivamente.