Conjunto

En matemáticas, un conjunto se define como la agrupación de elementos que comparten una propiedad en común y conforman un todo.El concepto de conjunto como objeto abstracto no comenzó a emplearse en matemáticas hasta el siglo XIX, a medida que se despejaban las dudas sobre la noción de infinito.Las contribuciones de Richard Dedekind al álgebra estaban formuladas en términos claramente conjuntistas, que aún prevalecen en la matemática moderna: relaciones de equivalencia, particiones, homomorfismos, etc., y él mismo explicitó las hipótesis y operaciones relativas a conjuntos que necesitó en su trabajo.La teoría de conjuntos como disciplina independiente se atribuye usualmente a Georg Cantor.La influencia de Dedekind y Cantor empezó a ser determinante a finales del siglo XIX, en el proceso de «axiomatización» de la matemática, en el que todos los objetos matemáticos, como los números, las funciones y las diversas estructuras, fueron construidos con base en los conjuntos.Un conjunto es una colección bien definida de objetos,dichos objetos pueden ser cualquier cosa: números, personas, letras, etc. Algunos ejemplos son: Los conjuntos se denotan habitualmente por letras mayúsculas.Los objetos que componen el conjunto se llaman elementos o miembros.Por ejemplo: Existen varias maneras de referirse a un conjunto.Sin embargo, para los conjuntos B y C se usa una definición extensiva, listando todos sus elementos explícitamente.Es habitual usar llaves para escribir los elementos de un conjunto, de modo que: Esta notación mediante llaves también se utiliza cuando los conjuntos se especifican de forma intensiva mediante una propiedad: Otra notación habitual para denotar por comprensión es: En estas expresiones los dos puntos («:») significan «tal que».En lugar de los dos puntos se utiliza también la barra vertical («|») u oblicua «/» .Un mismo conjunto puede especificarse de muchas maneras distintas, en particular extensivas o intensivas.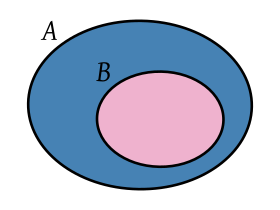Dos conjuntos A y B son disjuntos si no tienen ningún elemento en común.Así, en los ejemplos anteriores, se tiene que |A| = 4 (cuatro números), |B| = 3 (tres colores) y |F| = 10 (diez cuadrados).Sin embargo, existe una manera de comparar conjuntos infinitos entre sí, y se obtiene que existen conjuntos infinitos «más grandes» que otros.