Completar el cuadrado
a otra equivalente de la forma:
[1] En general, los procedimientos para completar el cuadrado consisten en construir, mediante operaciones algebraicas, un trinomio cuadrado perfecto a partir de una expresión que no lo es, y luego reducir el resultado a un binomio al cuadrado más (o menos) una constante.
Cuando se tiene un trinomio cuadrado perfecto, este se puede factorizar directamente a un binomio al cuadrado.
Si no se tiene un trinomio cuadrado perfecto, como por ejemplo
, este se puede manipular algebráicamente para construirlo.
Nótese que el término independiente 28 es igual a 25 + 3, Así que el trinomio dado es igual a
Esto que acabamos de hacer es uno de los procedimientos para completar el cuadrado.
Abajo se describen en detalle operaciones algebraicas para completar el cuadrado con cualquier trinomio cuadrado dado.
Observación: con respecto a la expresión resultante
Un método es elevando al cuadrado ambos miembros, lo cual generará dos resultados, debido a la presencia de una raíz de índice par (en este caso cuadrada).
+ b x + c = a
, los valores -h y k son respectivamente las coordenadas x e y del vértice de la parábola que representa graficamente a la función.
Si el valor de a es positivo, la parábola abre hacia arriba y k es el valor mínimo de la parábola, y si a es negativo, la parábola abre hacia abajo y k es el valor máximo de la parábola.
En general, h y k representan desplazamientos en el plano cartesiano de la parábola representada por la función
[2] El valor de h determina un desplazamiento con dirección horizontal tantas unidades lo indique su valor y en sentido opuesto a su signo, es decir, si h es positivo el desplazamiento se hace hacia la izquierda, mientras que si es negativo el desplazamiento se hace hacia la derecha.
Por ejemplo, si h es igual a -3, la parábola se desplazará 3 unidades hacia la derecha, y si h es igual a 5 la parábola se desplazará 5 unidades hacia la izquierda.
Por otro lado, el valor de k determina un desplazamiento con dirección vertical tantas unidades lo indique su valor, hacia arriba si es positivo y hacia abajo si es negativo.
Por ejemplo, si k es igual a -1, la parábola se desplazará una unidad hacia abajo, y si k es igual a 1 la parábola se desplazará una unidad hacia arriba.
En el ejemplo de la gráfica, h = -2, y k = 1.
se desplaza 2 unidades a la derecha y una hacia arriba, haciendo que su vértice sea el punto (2,1).
Considere completar el cuadrado para la siguiente ecuación:
representa el área de un rectángulo con lados
, el proceso de completar el cuadrado se puede ver como una manipulación visual de rectángulos.
en un cuadrado mayor resulta en una esquina que falta.
Completar el cuadrado se utiliza en: (left)
En matemáticas, completar el cuadrado se considera un mecanismo algebraico básico, y con frecuencia se aplica sin comentarios en cualquier cálculo involucrando polinomios cuadráticos.
La completación de cuadrados se utiliza para deducir la fórmula cuadrática.
Un ejemplo simple[5] es: Aplicación en cálculo integral.
Ahora, considérese el problema de encontrar esta antiderivada: El denominador es Sumando
De lo que resulta Sea la integral
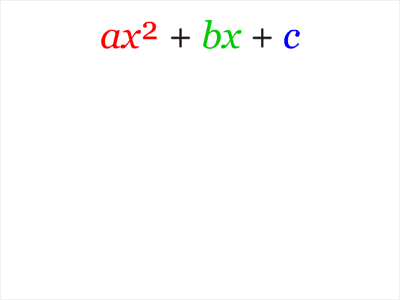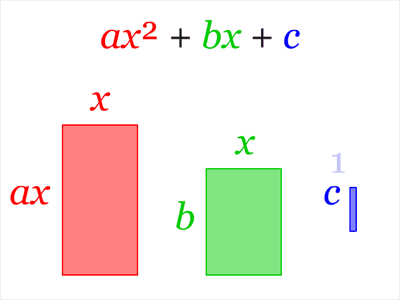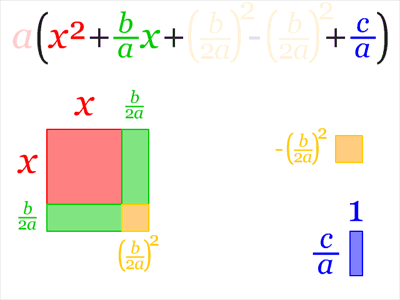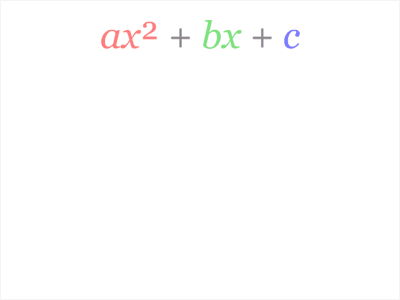

h = -2 y k = 1, así, el vértice de la parábola está en las coordenadas ( -h , k ) = (2, 1)
