Teoría del campo cristalino
La TCC fue desarrollada por los físicos Hans Bethe y John Hasbrouck van Vleck[1] en la década de 1930.
La TCC fue posteriormente combinada con la teoría de orbitales moleculares para producir la teoría del campo de ligandos que aunque resulta un poco más compleja también es más ajustada a la realidad, ya que se adentra además en la explicación del proceso de formación del enlace químico en los complejos metálicos.
Si se considera un campo repulsivo perfectamente esférico los cinco orbitales d deberían deformarse en la misma proporción y por lo tanto continuarían siendo degenerados, pero la TCC parte de la suposición de que los ligandos son cargas repulsivas puntuales, ubicadas en posiciones específicas del espacio, por lo tanto las repulsiones sobre los electrones de los orbitales d resultan asimétricas, lo que produce asimetrías en la manera en que deforman los orbitales causando que los cinco orbitales d de iguales energías (degenerados) se separen en varios grupos de diferente energía.
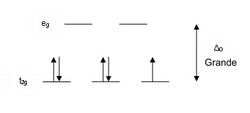
Si suponemos que estos seis ligandos puntuales se ubican sobre los seis ejes de un sistema cartesiano tridimensional con el ion metálico en el origen de coordenadas y observamos la figura con la forma de los orbitales d, estamos en condiciones de comenzar a analizar la teoría del campo cristalino: En esta disposición octaédrica los orbitales que resultan más gravemente deformados son los que poseen componentes mayoritarias sobre los ejes x, y, z. Observando el gráfico de orbitales d se puede notar que estos orbitales son el dz2 y el dx2-y2, mientras que los orbitales dxy, dxz y dyz reciben una interferencia mucho menor, esto causa que los orbitales d originalmente degenerados se separen en dos grupos con una diferencia de energía que se suele llamar Δoct.
Algunos ligandos solo producen un pequeño valor de Δ, mientras que otros generan una gran separación.
Las razones subyacentes a esto pueden ser explicadas por la teoría del campo de ligandos.
Ya que, como lo indica el principio de exclusión de Pauli, ningún electrón en un átomo puede tener sus cuatro números cuánticos iguales a otro cuando dos electrones ocupan un mismo orbital (es decir, ya tienen sus primeros tres números cuánticos iguales) deben hacerlo de modo que su cuarto número cuántico sea diferente, para el electrón solo existen dos estados cuánticos de espín posibles: -1/2 y +1/2, que comúnmente se llaman "espines opuestos").
Sin embargo existe, además, un cierto grado de repulsión entre electrones que ocupan un mismo orbital.
Los ligandos que causan una gran separación Δ en los orbitales atómicos d del metal se suelen referir como ligandos de campo fuerte, tales como por ejemplo el CN− y CO de la serie espectroquímica.
El ion octaédrico Fe(NO2)6]3− que posee 5 electrones d, muestra un diagrama de campo octaédrico donde todos los electrones se encuentran en el nivel t2g, este ion es por lo tanto un complejo de espín bajo.
En estos complejos resulta energéticamente más rentable para los electrones ocupar todos los orbitales siguiendo la regla de Hund, es decir haciéndolo con espines desapareados.
La brecha energética para un complejo metálico tetraédrico (con cuatro ligandos), Δtet es aproximadamente igual a 4/9 de Δoct.
Un compuesto que en su diagrama de separación energética muestra electrones con espines desapareados será paramagnético y se verá atraído por los campos magnéticos, mientras que un compuesto que no posea electrones desapareados en su diagrama energético será diamagnético y se verá débilmente repelido por los campos magnéticos.
Como ejemplo podemos considerar dos configuraciones de electrones d5 mostradas anteriormente en esta misma página.
En el ejemplo de alto espín (inferior) , la EECC es (3 x 2/5 Δoct) - (2 x 3/5 Δoct) = 0 - en este caso, la estabilización generada por los electrones en los orbitales inferiores es cancelada por el efecto desestabilizante de los electrones en los orbitales superiores.
Es así que según esta teoría la razón por la cual tantos complejos d8 son cuadrados planos es el enorme grado de estabilización cristalina que esta geometría produce para este número de electrones.
Los brillantes colores exhibidos por muchos compuestos de coordinación pueden ser explicados con facilidad por la TCC.
Sin embargo es bastante extraño que la energía del fotón absorbido se corresponda exactamente con la brecha Δ; ya que existen numerosos factores que también afectan la diferencia de energía entre el estado basal y los diferentes estados excitados, cosas tales como las repulsiones electrón-electrón y el efecto Jahn-Teller.