Una rama importante de la teoría de la elección social se dedica a la comparación de sistemas electorales , también conocidos como funciones de elección social . Vistos desde la perspectiva de la ciencia política , los sistemas electorales son reglas para llevar a cabo elecciones y determinar a los ganadores a partir de los votos emitidos. Desde la perspectiva de la economía , las matemáticas y la filosofía , una función de elección social es una función matemática que determina cómo una sociedad debería tomar decisiones, dada una colección de preferencias individuales.
En este artículo se analizan los métodos y los resultados de la comparación de distintos sistemas. Existen dos formas generales de comparar los sistemas de votación:
Los métodos de votación pueden evaluarse midiendo su precisión en elecciones simuladas al azar, con el objetivo de que sean fieles a las propiedades de las elecciones en la vida real. La primera evaluación de este tipo fue realizada por Chamberlin y Cohen en 1978, quienes midieron la frecuencia con la que ciertos sistemas no Condorcet elegían ganadores Condorcet. [1]
El marqués de Condorcet consideraba que las elecciones eran análogas a las votaciones de un jurado, en el que cada miembro expresa un juicio independiente sobre la calidad de los candidatos. Los candidatos difieren en términos de su mérito objetivo, pero los votantes tienen información imperfecta sobre los méritos relativos de los candidatos. Estos modelos de jurado a veces se conocen como modelos de valencia . Condorcet y su contemporáneo Laplace demostraron que, en un modelo de este tipo, la teoría de la votación podía reducirse a la probabilidad hallando la calidad esperada de cada candidato. [2]
El modelo del jurado implica varios conceptos naturales de precisión para los sistemas de votación bajo diferentes modelos:
Sin embargo, el modelo de Condorcet se basa en el supuesto extremadamente fuerte de errores independientes , es decir, que los votantes no estarán sistemáticamente sesgados a favor de un grupo de candidatos u otro. Esto suele ser poco realista: los votantes tienden a comunicarse entre sí, a formar partidos o ideologías políticas y a participar en otros comportamientos que pueden dar lugar a errores correlacionados .
En 1948, Duncan Black propuso un modelo espacial unidimensional de la votación, en el que consideraba que las elecciones estaban impulsadas por una ideología. [4] Sus ideas fueron ampliadas posteriormente por Anthony Downs. [5] Las opiniones de los votantes se consideran posiciones en un espacio de una o más dimensiones; los candidatos tienen posiciones en el mismo espacio; y los votantes eligen a los candidatos en orden de proximidad (medido según la distancia euclidiana o alguna otra métrica).
Los modelos espaciales implican una noción diferente de mérito para los sistemas de votación: cuanto más aceptable sea el candidato ganador como parámetro de ubicación para la distribución de los votantes, mejor será el sistema. Un espectro político es un modelo espacial unidimensional.
Los modelos de votación neutrales intentan minimizar el número de parámetros y, como ejemplo, el principio de no tener nada bajo la manga . El modelo más común de este tipo es el modelo de cultura anónima imparcial (o modelo de Dirichlet ). Estos modelos suponen que los votantes asignan a cada candidato una utilidad completamente al azar (a partir de una distribución uniforme ).
Tideman y Plassmann realizaron un estudio que demostró que un modelo espacial bidimensional daba un ajuste razonable a las reducciones de 3 candidatos de un gran conjunto de clasificaciones electorales. Los modelos de jurado, los modelos neutrales y los modelos espaciales unidimensionales eran todos inadecuados. [6] Observaron los ciclos de Condorcet en las preferencias de los votantes (un ejemplo de los cuales es A siendo preferido a B por una mayoría de votantes, B a C y C a A) y encontraron que el número de ellos era consistente con los efectos de muestra pequeña, concluyendo que "los ciclos de votación ocurrirán muy raramente, si es que ocurren, en elecciones con muchos votantes". La relevancia del tamaño de la muestra había sido estudiada previamente por Gordon Tullock , quien argumentó gráficamente que aunque los electorados finitos serán propensos a los ciclos, el área en la que los candidatos pueden dar lugar a ciclos se reduce a medida que aumenta el número de votantes. [7]
En un modelo utilitarista , los votantes clasifican a los candidatos según su utilidad. El ganador legítimo, según este modelo, es el candidato que maximiza la utilidad social general. Un modelo utilitarista se diferencia de un modelo espacial en varios aspectos importantes:
De la última propiedad se desprende que ningún sistema electoral que dé la misma influencia a todos los votantes tiene probabilidades de lograr la máxima utilidad social. Los casos extremos de conflicto entre las pretensiones del utilitarismo y la democracia se conocen como la " tiranía de la mayoría ". Véanse los comentarios de Laslier, Merlin y Nurmi en el artículo de Laslier. [8]
James Mill parece haber sido el primero en afirmar la existencia de una conexión a priori entre la democracia y el utilitarismo (véase el artículo de la Enciclopedia de Stanford). [9]
Supongamos que el i- ésimo candidato en una elección tiene mérito x i (podemos suponer que x i ~ N (0,σ 2 ) [10] ), y que el nivel de aprobación del votante j para el candidato i puede escribirse como x i + ε ij (supondremos que los ε ij son iid. N (0,τ 2 )). Suponemos que un votante clasifica a los candidatos en orden decreciente de aprobación. Podemos interpretar ε ij como el error en la valoración del votante j del candidato i y considerar que un método de votación tiene la tarea de encontrar al candidato de mayor mérito.
Cada votante clasificará al mejor de los dos candidatos por encima del menos bueno con una probabilidad determinada p (que bajo el modelo normal esbozado aquí es igual a , como se puede confirmar a partir de una fórmula estándar para integrales gaussianas sobre un cuadrante [ cita requerida ] ). El teorema del jurado de Condorcet muestra que mientras p > 1 ⁄ 2 , el voto mayoritario de un jurado será una mejor guía para los méritos relativos de dos candidatos que la opinión de cualquier miembro individual.
Peyton Young demostró que hay otras tres propiedades que se aplican a los votos entre un número arbitrario de candidatos, lo que sugiere que Condorcet conocía la primera y la tercera de ellas. [11]
Robert F. Bordley construyó un modelo "utilitario" que es una ligera variante del modelo del jurado de Condorcet. [12] Consideró que la tarea de un método de votación era la de encontrar al candidato que tuviera la mayor aprobación total del electorado, es decir, la suma más alta de los niveles de aprobación de los votantes individuales. Este modelo tiene sentido incluso con σ 2 = 0, en cuyo caso p toma el valor donde n es el número de votantes. Realizó una evaluación bajo este modelo y descubrió, como se esperaba, que el recuento de Bordley era el más preciso.
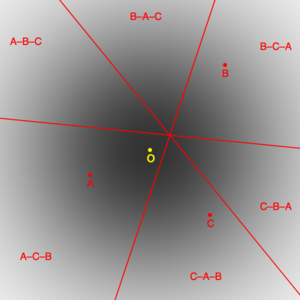
Se puede construir una elección simulada a partir de una distribución de votantes en un espacio adecuado. La ilustración muestra votantes que satisfacen una distribución gaussiana bivariada centrada en O. Hay 3 candidatos generados aleatoriamente, A, B y C. El espacio está dividido en 6 segmentos por 3 líneas, y los votantes de cada segmento tienen las mismas preferencias de candidato. La proporción de votantes que ordenan a los candidatos de cualquier manera está dada por la integral de la distribución de votantes sobre el segmento asociado.
Las proporciones correspondientes a las 6 posibles ordenaciones de candidatos determinan los resultados que arrojan los distintos sistemas de votación. Se considera que aquellos que eligen al mejor candidato, es decir, al candidato más cercano a O (que en este caso es A), han dado un resultado correcto, y aquellos que eligen a otro han mostrado un error. Al observar los resultados de un gran número de candidatos generados aleatoriamente, se pueden medir las propiedades empíricas de los sistemas de votación.
El protocolo de evaluación que se describe aquí se basa en el descrito por Tideman y Plassmann. [6] Las evaluaciones de este tipo son más comunes en los sistemas electorales de ganador único. Los sistemas de votación por orden de preferencia encajan más naturalmente en el marco, pero otros tipos de votación (como el sistema de votación por mayoría simple y el sistema de votación por aprobación ) pueden adaptarse con un esfuerzo mayor o menor.
El protocolo de evaluación se puede variar de varias maneras:
Uno de los principales usos de las evaluaciones es comparar la precisión de los sistemas de votación cuando los votantes votan sinceramente. Si un número infinito de votantes satisface una distribución gaussiana, entonces el ganador legítimo de una elección puede considerarse el candidato más cercano a la media/mediana, y la precisión de un método puede identificarse con la proporción de elecciones en las que el ganador legítimo es elegido. El teorema del votante mediano garantiza que todos los sistemas de Condorcet darán una precisión del 100% (y lo mismo se aplica al método de Coombs [14] ).
Las evaluaciones publicadas en artículos de investigación utilizan gaussianas multidimensionales, lo que hace que el cálculo sea numéricamente difícil. [1] [15] [16] [17] El número de votantes se mantiene finito y el número de candidatos es necesariamente pequeño.
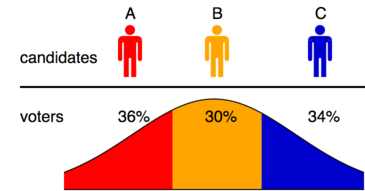
El cálculo es mucho más sencillo en una única dimensión, que permite un número infinito de votantes y un número arbitrario m de candidatos. Los resultados para este caso sencillo se muestran en la primera tabla, que es directamente comparable con la Tabla 5 (1000 votantes, dispersión media) del artículo citado de Chamberlin y Cohen. Los candidatos fueron seleccionados aleatoriamente de la distribución de votantes y se incluyó un único método de Condorcet ( Minimax ) en los ensayos para su confirmación.
El desempeño relativamente pobre del voto alternativo (IRV) se explica por la conocida y común fuente de error ilustrada en el diagrama, en el que la elección satisface un modelo espacial univariado y el ganador legítimo B será eliminado en la primera vuelta. Un problema similar existe en todas las dimensiones.
Una medida alternativa de precisión es la distancia media de los votantes respecto del ganador (en la que cuanto menor sea, mejor). Es poco probable que esto cambie la clasificación de los métodos de votación, pero es la preferida por quienes interpretan la distancia como desutilidad. La segunda tabla muestra la distancia media (en desviaciones estándar) menos (que es la distancia media de una variable respecto del centro de una distribución gaussiana estándar) para 10 candidatos bajo el mismo modelo.
James Green-Armytage et al. publicaron un estudio en el que evaluaron la vulnerabilidad de varios sistemas de votación a la manipulación por parte de los votantes. [18] Dicen poco sobre cómo adaptaron su evaluación para este propósito, mencionando simplemente que "requiere una programación creativa". Un artículo anterior del primer autor brinda un poco más de detalles. [19]
El número de candidatos en sus elecciones simuladas se limitó a 3. Esto elimina la distinción entre ciertos sistemas; por ejemplo, el método de Black y el método Dasgupta-Maskin son equivalentes para 3 candidatos.
Las conclusiones del estudio son difíciles de resumir, pero el recuento de Borda tuvo un mal desempeño; el Minimax fue algo vulnerable; y el IRV fue altamente resistente. Los autores demostraron que limitar cualquier método a elecciones sin un ganador de Condorcet (eligiendo al ganador de Condorcet cuando lo hubo) nunca aumentaría su susceptibilidad al voto táctico . Informaron que el sistema "Condorcet-Hare" que utiliza el IRV como desempate para elecciones no resueltas por el criterio de Condorcet era tan resistente al voto táctico como el IRV por sí solo y más preciso. Condorcet-Hare es equivalente al método de Copeland con un desempate IRV en elecciones con 3 candidatos.
Algunos sistemas, y en particular el recuento de Borda, son vulnerables cuando la distribución de candidatos se desplaza con respecto a la distribución de votantes. La tabla adjunta muestra la precisión del recuento de Borda (en porcentaje) cuando una población infinita de votantes satisface una distribución gaussiana univariante y se extraen m candidatos de una distribución similar compensada por x distribuciones estándar. El color rojo indica cifras que son peores que las aleatorias. Recuerde que todos los métodos de Condorcet dan una precisión del 100 % para este problema. (Y observe que la reducción de la precisión a medida que x aumenta no se observa cuando solo hay 3 candidatos).
La sensibilidad a la distribución de candidatos puede considerarse una cuestión de precisión o de resistencia a la manipulación. Si se espera que, en el curso de los acontecimientos, los candidatos provengan naturalmente de la misma distribución que los votantes, entonces cualquier desplazamiento será visto como un intento de subversión; pero si se piensa que los factores que determinan la viabilidad de la candidatura (como el respaldo financiero) pueden estar correlacionados con la posición ideológica, entonces se lo considerará más en términos de precisión.
Las evaluaciones publicadas adoptan diferentes puntos de vista sobre la distribución de candidatos. Algunos simplemente suponen que los candidatos provienen de la misma distribución que los votantes. [16] [18] Varios artículos más antiguos suponen que las medias son iguales, pero permiten que la distribución de candidatos sea más o menos ajustada que la distribución de votantes. [20] [1] Un artículo de Tideman y Plassmann aproxima la relación entre las distribuciones de candidatos y votantes basándose en mediciones empíricas. [15] Esto es menos realista de lo que parece, ya que no permite que la distribución de candidatos se ajuste para explotar cualquier debilidad en el sistema de votación. Un artículo de James Green-Armytage analiza la distribución de candidatos como un tema separado, considerándola como una forma de manipulación y midiendo los efectos de la entrada y salida estratégicas. No es sorprendente que encuentre que el recuento de Borda es particularmente vulnerable. [19]
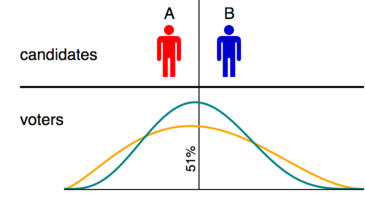
La tarea de un sistema de votación basado en un modelo espacial es identificar al candidato cuya posición represente con mayor precisión la distribución de las opiniones de los votantes. Esto equivale a elegir un parámetro de ubicación para la distribución a partir del conjunto de alternativas ofrecidas por los candidatos. Los parámetros de ubicación pueden basarse en la media, la mediana o la moda; pero como las papeletas de votación por orden de preferencia proporcionan únicamente información ordinal, la mediana es la única estadística aceptable.
Esto se puede ver en el diagrama, que ilustra dos elecciones simuladas con los mismos candidatos pero con diferentes distribuciones de votantes. En ambos casos, el punto medio entre los candidatos es el percentil 51 de la distribución de votantes; por lo tanto, el 51% de los votantes prefiere A y el 49% prefiere B. Si consideramos que un método de votación es correcto si elige al candidato más cercano a la mediana de la población de votantes, entonces, como la mediana está necesariamente ligeramente a la izquierda de la línea del 51%, un método de votación se considerará correcto si elige A en cada caso.
La media de la distribución verde azulado también está ligeramente a la izquierda de la línea del 51%, pero la media de la distribución naranja está ligeramente a la derecha. Por lo tanto, si consideramos que un método de votación es correcto si elige al candidato más cercano a la media de la población de votantes, entonces un método no podrá obtener la puntuación máxima a menos que produzca diferentes ganadores de las mismas papeletas en las dos elecciones. Claramente, esto imputará errores espurios a los métodos de votación. El mismo problema surgirá para cualquier medida cardinal de ubicación; solo la mediana da resultados consistentes.
La mediana no está definida para distribuciones multivariadas, pero la mediana univariante tiene una propiedad que se generaliza convenientemente. La mediana de una distribución es la posición cuya distancia promedio desde todos los puntos dentro de la distribución es más pequeña. Esta definición se generaliza a la mediana geométrica en múltiples dimensiones. La distancia se define a menudo como una función de desutilidad del votante .
Si tenemos un conjunto de candidatos y una población de votantes, entonces no es necesario resolver el problema computacionalmente difícil de encontrar la mediana geométrica de los votantes y luego identificar al candidato más cercano a ella; en cambio, podemos identificar al candidato cuya distancia promedio con respecto a los votantes sea mínima. Esta es la métrica que se ha utilizado generalmente desde Merrill en adelante; [20] véase también Green-Armytage y Darlington. [19] [16]
El candidato más cercano a la mediana geométrica de la distribución de votantes puede denominarse "ganador espacial".
Los datos de elecciones reales pueden analizarse para comparar los efectos de diferentes sistemas, ya sea comparando entre países o aplicando sistemas electorales alternativos a los datos de elecciones reales. Los resultados electorales pueden compararse a través de índices de democracia , medidas de fragmentación política , participación electoral , [21] [22] eficacia política y varios indicadores económicos y judiciales. Los criterios prácticos para evaluar las elecciones reales incluyen la proporción de votos desperdiciados , la complejidad del recuento de votos , la proporcionalidad y las barreras de entrada para nuevos movimientos políticos. [23] Surgen oportunidades adicionales para la comparación de elecciones reales a través de las reformas electorales .
Un ejemplo canadiense de tal oportunidad se ve en la ciudad de Edmonton (Canadá), que pasó del sistema de votación mayoritaria simple en las elecciones generales de Alberta de 1917 al sistema de votación en bloque con cinco miembros en las elecciones generales de Alberta de 1921 , al sistema de votación única transferible con cinco miembros en las elecciones generales de Alberta de 1926 y luego al sistema de votación por mayoría simple en las elecciones generales de Alberta de 1959. Un partido arrasó con todos los escaños de Edmonton en 1917, 1921 y 1959. Bajo el sistema de votación por mayoría simple en 1926, fueron elegidos dos conservadores, un liberal, un laborista y un diputado de United Farmers.
Tradicionalmente, los méritos de los distintos sistemas electorales se han discutido con referencia a criterios lógicos. Estos tienen la forma de reglas de inferencia para las decisiones electorales, que permiten deducir, por ejemplo, que "si E y E ' son elecciones tales que R ( E , E '), y si A es el legítimo ganador de E , entonces A es el legítimo ganador de E ' ".
Los criterios absolutos establecen que, si el conjunto de papeletas es de una determinada manera, un determinado candidato debe ganar o no.
Se trata de criterios que establecen que, si un determinado candidato gana en una circunstancia, el mismo candidato debe (o no) ganar en una circunstancia relacionada.
Se trata de criterios relacionados con el proceso de recuento de votos y determinación de un ganador.
Se trata de criterios relacionados con el incentivo que tiene un votante para utilizar determinadas formas de estrategia. También podrían considerarse criterios de resultados relativos; sin embargo, a diferencia de los criterios de esa sección, estos criterios son directamente relevantes para los votantes; el hecho de que un método cumpla con estos criterios puede simplificar el proceso de determinar el voto estratégico óptimo.
Las papeletas se pueden distinguir en dos categorías: cardinales y ordinales , donde las papeletas cardinales solicitan medidas individuales de apoyo para cada candidato y las papeletas ordinales solicitan medidas relativas de apoyo. Algunos métodos no encajan perfectamente en una categoría, como STAR, que pide al votante que dé calificaciones independientes para cada candidato, pero utiliza tanto las calificaciones absolutas como las relativas para determinar el ganador. Comparar dos métodos basándose únicamente en el tipo de papeleta es principalmente una cuestión de preferencia de la experiencia del votante, a menos que el tipo de papeleta esté relacionado con uno de los otros criterios matemáticos enumerados aquí.
El criterio A es "más fuerte" que el B si satisfacer A implica satisfacer B. Por ejemplo, el criterio de Condorcet es más fuerte que el criterio de mayoría, porque todos los ganadores de la mayoría son ganadores de Condorcet. Por lo tanto, cualquier método de votación que satisfaga el criterio de Condorcet debe satisfacer el criterio de mayoría.
La siguiente tabla muestra cuáles de los criterios anteriores se cumplen en varios métodos de ganador único. No se enumeran todos los criterios.
Los teóricos de la elección social utilizan las preocupaciones planteadas anteriormente para diseñar sistemas precisos y resistentes a la manipulación. Sin embargo, también existen razones prácticas por las que un sistema puede ser más aceptable socialmente que otro, que se enmarcan en los campos de la elección pública y la ciencia política . [8] [16] Algunas consideraciones prácticas importantes incluyen:
Otras consideraciones incluyen las barreras de entrada a la competencia política [28] y la probabilidad de un gobierno paralizado . [29]
Los sistemas electorales con múltiples ganadores, en el mejor de los casos, buscan producir asambleas representativas en un sentido más amplio que el de tomar las mismas decisiones que se tomarían con votos de un solo ganador. También pueden ser una vía para que un solo partido barriera con los escaños de una ciudad, si se utiliza un sistema no proporcional, como la votación en bloque por pluralidad o la votación por boleta .
Para evaluar el desempeño de los métodos de votación con múltiples ganadores se requieren métricas diferentes a las que se utilizan para los sistemas con un solo ganador. Se han propuesto las siguientes:
La siguiente tabla muestra cuáles de los criterios anteriores se cumplen con varios métodos de ganadores múltiples.
{{cite book}}: |journal=ignorado ( ayuda )