Producto vectorial

Mathematical operation on vectors in 3D space

El producto vectorial con respecto a un sistema de coordenadas diestro

En matemáticas , el producto vectorial o producto vectorial (en ocasiones producto de área dirigida , para enfatizar su significado geométrico) es una operación binaria sobre dos vectores en un espacio vectorial euclidiano orientado tridimensional (nombrado aquí ), y se denota con el símbolo . Dados dos vectores linealmente independientes a y b , el producto vectorial, a × b (léase "a cruz b"), es un vector que es perpendicular tanto a a como a b , ^[1] y, por lo tanto, normal al plano que los contiene. Tiene muchas aplicaciones en matemáticas, física , ingeniería y programación informática . No debe confundirse con el producto escalar (producto de proyección). ${\displaystyle E}$ ${\displaystyle \times }$

La magnitud del producto vectorial es igual al área de un paralelogramo con los vectores de los lados; en particular, la magnitud del producto de dos vectores perpendiculares es el producto de sus longitudes. Las unidades del producto vectorial son el producto de las unidades de cada vector. Si dos vectores son paralelos o antiparalelos (es decir, son linealmente dependientes), o si alguno de ellos tiene longitud cero, entonces su producto vectorial es cero. ^[2]

El producto vectorial es anticonmutativo (es decir, a × b = − b × a ) y es distributivo sobre la suma, es decir, a × ( b + c ) = a × b + a × c . ^[1] El espacio junto con el producto vectorial es un álgebra sobre los números reales , que no es ni conmutativa ni asociativa , sino un álgebra de Lie donde el producto vectorial es el corchete de Lie . ${\displaystyle E}$

Al igual que el producto escalar, depende de la métrica del espacio euclidiano , pero a diferencia de este, también depende de la elección de la orientación (o " lateralidad ") del espacio (por eso se necesita un espacio orientado). El vector resultante es invariante de la rotación de la base. Debido a la dependencia de la lateralidad , se dice que el producto vectorial es un pseudovector .

En relación con el producto vectorial, el producto exterior de vectores se puede utilizar en dimensiones arbitrarias (con un resultado bivectorial o de 2 formas ) y es independiente de la orientación del espacio.

El producto se puede generalizar de varias maneras, utilizando la orientación y la estructura métrica al igual que para el producto vectorial tradicional en 3 dimensiones; uno puede, en n dimensiones, tomar el producto de n − 1 vectores para producir un vector perpendicular a todos ellos. Pero si el producto se limita a productos binarios no triviales con resultados vectoriales, solo existe en tres y siete dimensiones. ^[3] Sin embargo, el producto vectorial en siete dimensiones tiene propiedades indeseables (por ejemplo, no satisface la identidad de Jacobi ), por lo que no se utiliza en física matemática para representar cantidades como el espacio-tiempo multidimensional . ^[4] (Véase § Generalizaciones a continuación para otras dimensiones).

Definición

Encontrar la dirección del producto vectorial mediante la regla de la mano derecha

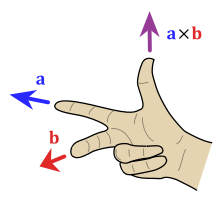
El producto vectorial de dos vectores a y b se define solo en el espacio tridimensional y se denota por a × b . En física y matemáticas aplicadas , se utiliza a menudo la notación de cuña a ∧ b (junto con el nombre de producto vectorial ), ^{[5] [6] [7]} aunque en matemáticas puras dicha notación suele reservarse solo para el producto exterior, una abstracción del producto vectorial en n dimensiones.

El producto vectorial a × b se define como un vector c que es perpendicular (ortogonal) tanto a a como a b , con una dirección dada por la regla de la mano derecha ^[1] y una magnitud igual al área del paralelogramo que abarcan los vectores. ^[2]

El producto vectorial se define mediante la fórmula ^{[8] [9]}

${\displaystyle \mathbf {a} \times \mathbf {b} =\|\mathbf {a} \|\|\mathbf {b} \|\sin(\theta )\,\mathbf {n} ,}$

dónde

θ es el ángulo entre a y b en el plano que los contiene (por lo tanto, está entre 0° y 180°),

‖a‖ y ‖b‖ son las magnitudes de los vectores a y b ,

n es un vector unitario perpendicular al plano que contiene a y b , con dirección tal que el conjunto ordenado ( a , b , n ) está orientado positivamente .

Si los vectores a y b son paralelos (es decir, el ángulo θ entre ellos es 0° o 180°), por la fórmula anterior, el producto vectorial de a y b es el vector cero 0 .

Dirección

El producto vectorial a × b (vertical, en violeta) cambia a medida que cambia el ángulo entre los vectores a (azul) y b (rojo). El producto vectorial siempre es ortogonal a ambos vectores y tiene magnitud cero cuando los vectores son paralelos y magnitud máxima ‖ a ‖‖ b ‖ cuando son ortogonales.

La dirección del vector n depende de la orientación elegida en el espacio. Convencionalmente, se da por la regla de la mano derecha, donde uno simplemente apunta el dedo índice de la mano derecha en la dirección de a y el dedo medio en la dirección de b . Entonces, el vector n sale del pulgar (ver la imagen adyacente). El uso de esta regla implica que el producto vectorial es anticonmutativo ; es decir, b × a = −( a × b ) . Al apuntar el dedo índice hacia b primero, y luego apuntar el dedo medio hacia a , el pulgar será forzado en la dirección opuesta, invirtiendo el signo del vector producto.

Como el operador del producto vectorial depende de la orientación del espacio, en general el producto vectorial de dos vectores no es un vector "verdadero", sino un pseudovector . Consulte § Lateralidad para obtener más detalles.

Nombres y origen

Según la regla de Sarrus , el determinante de una matriz 3×3 implica multiplicaciones entre elementos de la matriz identificados por diagonales cruzadas.

En 1842, William Rowan Hamilton describió por primera vez el álgebra de cuaterniones y el producto de Hamilton no conmutativo. En particular, cuando se realiza el producto de Hamilton de dos vectores (es decir, cuaterniones puros con parte escalar cero), se obtiene un cuaternión con una parte escalar y una parte vectorial. La parte escalar y vectorial de este producto de Hamilton corresponde al negativo del producto escalar y el producto vectorial de los dos vectores.

En 1881, Josiah Willard Gibbs , ^[10] e independientemente Oliver Heaviside , introdujeron la notación tanto para el producto escalar como para el producto vectorial utilizando un punto ( a ⋅ b ) y una "×" ( a × b ), respectivamente, para denotarlos. ^[11]

En 1877, para enfatizar el hecho de que el resultado de un producto escalar es un escalar mientras que el resultado de un producto vectorial es un vector , William Kingdon Clifford acuñó los nombres alternativos producto escalar y producto vectorial para las dos operaciones. ^[11] Estos nombres alternativos todavía se usan ampliamente en la literatura.

Tanto la notación cruzada ( a × b ) como el nombre producto vectorial posiblemente se inspiraron en el hecho de que cada componente escalar de a × b se calcula multiplicando componentes no correspondientes de a y b . Por el contrario, un producto escalar a ⋅ b implica multiplicaciones entre componentes correspondientes de a y b . Como se explica a continuación, el producto vectorial se puede expresar en forma de determinante de una matriz especial de 3 × 3 . Según la regla de Sarrus , esto implica multiplicaciones entre elementos de la matriz identificados por diagonales cruzadas.

Computación

Notación de coordenadas

Vectores de base estándar ( i , j , k , también denotados e ₁ , e ₂ , e ₃ ) y componentes vectoriales de a ( a _x , a _y , a _z , también denotados a ₁ , a ₂ , a ₃ )

Si ( i , j , k ) es una base ortonormal orientada positivamente, los vectores base satisfacen las siguientes igualdades ^[1]

${\displaystyle {\begin{alignedat}{2}\mathbf {\color {blue}{i}} &\times \mathbf {\color {red}{j}} &&=\mathbf {\color {green}{k}} \\\mathbf {\color {red}{j}} &\times \mathbf {\color {green}{k}} &&=\mathbf {\color {blue}{i}} \\\mathbf {\color {green}{k}} &\times \mathbf {\color {blue}{i}} &&=\mathbf {\color {red}{j}} \end{alignedat}}}$

lo que implica, por la anticonmutatividad del producto vectorial, que

${\displaystyle {\begin{alignedat}{2}\mathbf {\color {red}{j}} &\times \mathbf {\color {blue}{i}} &&=-\mathbf {\color {green}{k}} \\\mathbf {\color {green}{k}} &\times \mathbf {\color {red}{j}} &&=-\mathbf {\color {blue}{i}} \\\mathbf {\color {blue}{i}} &\times \mathbf {\color {green}{k}} &&=-\mathbf {\color {red}{j}} \end{alignedat}}}$

La anticonmutatividad del producto vectorial (y la obvia falta de independencia lineal) también implica que

${\displaystyle \mathbf {\color {blue}{i}} \times \mathbf {\color {blue}{i}} =\mathbf {\color {red}{j}} \times \mathbf {\color {red}{j}} =\mathbf {\color {green}{k}} \times \mathbf {\color {green}{k}} =\mathbf {0} }$(el vector cero ).

Estas igualdades, junto con la distributividad y la linealidad del producto vectorial (aunque ninguna de ellas se desprende fácilmente de la definición dada anteriormente), son suficientes para determinar el producto vectorial de dos vectores cualesquiera a y b . Cada vector puede definirse como la suma de tres componentes ortogonales paralelas a los vectores base estándar:

${\displaystyle {\begin{alignedat}{3}\mathbf {a} &=a_{1}\mathbf {\color {blue}{i}} &&+a_{2}\mathbf {\color {red}{j}} &&+a_{3}\mathbf {\color {green}{k}} \\\mathbf {b} &=b_{1}\mathbf {\color {blue}{i}} &&+b_{2}\mathbf {\color {red}{j}} &&+b_{3}\mathbf {\color {green}{k}} \end{alignedat}}}$

Su producto vectorial a × b se puede desarrollar utilizando la distributividad:

${\displaystyle {\begin{aligned}\mathbf {a} \times \mathbf {b} ={}&(a_{1}\mathbf {\color {blue}{i}} +a_{2}\mathbf {\color {red}{j}} +a_{3}\mathbf {\color {green}{k}} )\times (b_{1}\mathbf {\color {blue}{i}} +b_{2}\mathbf {\color {red}{j}} +b_{3}\mathbf {\color {green}{k}} )\\={}&a_{1}b_{1}(\mathbf {\color {blue}{i}} \times \mathbf {\color {blue}{i}} )+a_{1}b_{2}(\mathbf {\color {blue}{i}} \times \mathbf {\color {red}{j}} )+a_{1}b_{3}(\mathbf {\color {blue}{i}} \times \mathbf {\color {green}{k}} )+{}\\&a_{2}b_{1}(\mathbf {\color {red}{j}} \times \mathbf {\color {blue}{i}} )+a_{2}b_{2}(\mathbf {\color {red}{j}} \times \mathbf {\color {red}{j}} )+a_{2}b_{3}(\mathbf {\color {red}{j}} \times \mathbf {\color {green}{k}} )+{}\\&a_{3}b_{1}(\mathbf {\color {green}{k}} \times \mathbf {\color {blue}{i}} )+a_{3}b_{2}(\mathbf {\color {green}{k}} \times \mathbf {\color {red}{j}} )+a_{3}b_{3}(\mathbf {\color {green}{k}} \times \mathbf {\color {green}{k}} )\\\end{aligned}}}$

Esto puede interpretarse como la descomposición de a × b en la suma de nueve productos cruzados más simples que involucran vectores alineados con i , j o ​​k . Cada uno de estos nueve productos cruzados opera sobre dos vectores que son fáciles de manejar ya que son paralelos u ortogonales entre sí. A partir de esta descomposición, utilizando las igualdades mencionadas anteriormente y reuniendo términos similares, obtenemos:

${\displaystyle {\begin{aligned}\mathbf {a} \times \mathbf {b} ={}&\quad \ a_{1}b_{1}\mathbf {0} +a_{1}b_{2}\mathbf {\color {green}{k}} -a_{1}b_{3}\mathbf {\color {red}{j}} \\&-a_{2}b_{1}\mathbf {\color {green}{k}} +a_{2}b_{2}\mathbf {0} +a_{2}b_{3}\mathbf {\color {blue}{i}} \\&+a_{3}b_{1}\mathbf {\color {red}{j}} \ -a_{3}b_{2}\mathbf {\color {blue}{i}} \ +a_{3}b_{3}\mathbf {0} \\={}&(a_{2}b_{3}-a_{3}b_{2})\mathbf {\color {blue}{i}} +(a_{3}b_{1}-a_{1}b_{3})\mathbf {\color {red}{j}} +(a_{1}b_{2}-a_{2}b_{1})\mathbf {\color {green}{k}} \\\end{aligned}}}$

lo que significa que los tres componentes escalares del vector resultante s = s ₁ i + s ₂ j + s ₃ k = a × b son

${\displaystyle {\begin{aligned}s_{1}&=a_{2}b_{3}-a_{3}b_{2}\\s_{2}&=a_{3}b_{1}-a_{1}b_{3}\\s_{3}&=a_{1}b_{2}-a_{2}b_{1}\end{aligned}}}$

Usando vectores columna , podemos representar el mismo resultado de la siguiente manera:

${\displaystyle {\begin{bmatrix}s_{1}\\s_{2}\\s_{3}\end{bmatrix}}={\begin{bmatrix}a_{2}b_{3}-a_{3}b_{2}\\a_{3}b_{1}-a_{1}b_{3}\\a_{1}b_{2}-a_{2}b_{1}\end{bmatrix}}}$

Notación matricial

Uso de la regla de Sarrus para encontrar el producto vectorial de a y b

El producto vectorial también se puede expresar como determinante formal : ^{[nota 1] [1]}

${\displaystyle \mathbf {a\times b} ={\begin{vmatrix}\mathbf {i} &\mathbf {j} &\mathbf {k} \\a_{1}&a_{2}&a_{3}\\b_{1}&b_{2}&b_{3}\\\end{vmatrix}}}$

Este determinante se puede calcular utilizando la regla de Sarrus o la expansión de cofactores . Utilizando la regla de Sarrus, se expande a

${\displaystyle {\begin{aligned}\mathbf {a\times b} &=(a_{2}b_{3}\mathbf {i} +a_{3}b_{1}\mathbf {j} +a_{1}b_{2}\mathbf {k} )-(a_{3}b_{2}\mathbf {i} +a_{1}b_{3}\mathbf {j} +a_{2}b_{1}\mathbf {k} )\\&=(a_{2}b_{3}-a_{3}b_{2})\mathbf {i} +(a_{3}b_{1}-a_{1}b_{3})\mathbf {j} +(a_{1}b_{2}-a_{2}b_{1})\mathbf {k} .\end{aligned}}}$

que da directamente los componentes del vector resultante.

Uso de tensores de Levi-Civita

• En cualquier base, el producto vectorial viene dado por la fórmula tensorial donde es el tensor covariante de Levi-Civita (observamos la posición de los índices). Esto corresponde a la fórmula intrínseca que se da aquí. ${\displaystyle a\times b}$ ${\displaystyle E_{ijk}a^{i}b^{j}}$ ${\displaystyle E_{ijk}}$
• En una base ortonormal que tiene la misma orientación que el espacio , se obtiene mediante la fórmula pseudotensorial , donde es el símbolo de Levi-Civita (que es un pseudotensor). Esa es la fórmula que se utiliza en la física cotidiana, pero funciona solo para esta elección especial de base. ${\displaystyle a\times b}$ ${\displaystyle \varepsilon _{ijk}a^{i}b^{j}}$ ${\displaystyle \varepsilon _{ijk}}$
• En cualquier base ortonormal, viene dada por la fórmula pseudo-tensorial donde indica si la base tiene la misma orientación que el espacio o no. ${\displaystyle a\times b}$ ${\displaystyle (-1)^{B}\varepsilon _{ijk}a^{i}b^{j}}$ ${\displaystyle (-1)^{B}=\pm 1}$

La última fórmula evita tener que cambiar la orientación del espacio cuando invertimos una base ortonormal.

Propiedades

Significado geométrico

Figura 1. El área de un paralelogramo como la magnitud de un producto vectorial

Figura 2. Tres vectores que definen un paralelepípedo

La magnitud del producto vectorial se puede interpretar como el área positiva del paralelogramo que tiene a y b como lados (ver Figura 1): ^[1] $${\displaystyle \left\|\mathbf {a} \times \mathbf {b} \right\|=\left\|\mathbf {a} \right\|\left\|\mathbf {b} \right\|\left|\sin \theta \right|.}$$

De hecho, también se puede calcular el volumen V de un paralelepípedo que tiene a , b y c como aristas utilizando una combinación de un producto vectorial y un producto escalar, llamado producto triple escalar (véase la Figura 2):

${\displaystyle \mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} )=\mathbf {b} \cdot (\mathbf {c} \times \mathbf {a} )=\mathbf {c} \cdot (\mathbf {a} \times \mathbf {b} ).}$

Como el resultado del triple producto escalar puede ser negativo, el volumen del paralelepípedo viene dado por su valor absoluto:

${\displaystyle V=|\mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} )|.}$

Como la magnitud del producto vectorial se calcula mediante el seno del ángulo entre sus argumentos, el producto vectorial puede considerarse como una medida de perpendicularidad , de la misma manera que el producto escalar es una medida de paralelismo . Dados dos vectores unitarios , su producto vectorial tiene una magnitud de 1 si los dos son perpendiculares y una magnitud de cero si los dos son paralelos. El producto escalar de dos vectores unitarios se comporta de manera exactamente opuesta: es cero cuando los vectores unitarios son perpendiculares y 1 si los vectores unitarios son paralelos.

Los vectores unitarios permiten dos identidades convenientes: el producto escalar de dos vectores unitarios da como resultado el coseno (que puede ser positivo o negativo) del ángulo entre los dos vectores unitarios. La magnitud del producto vectorial de los dos vectores unitarios da como resultado el seno (que siempre será positivo).

Propiedades algebraicas

Producto vectorial de la multiplicación escalar . Izquierda: Descomposición de b en componentes paralela y perpendicular a a . Derecha: Escala de los componentes perpendiculares por un número real positivo r (si es negativo, b y el producto vectorial se invierten).

Distributividad del producto vectorial sobre la suma de vectores. Izquierda: Los vectores b y c se descomponen en componentes paralelas y perpendiculares a a . Derecha: Las componentes paralelas se desvanecen en el producto vectorial, solo permanecen las componentes perpendiculares que se muestran en el plano perpendicular a a . ^[12]

Los dos productos cruzados triples no equivalentes de tres vectores a , b , c . En cada caso, dos vectores definen un plano, el otro está fuera del plano y se puede dividir en componentes paralelas y perpendiculares al producto cruzado de los vectores que definen el plano. Estos componentes se pueden encontrar por proyección y rechazo de vectores . El producto triple está en el plano y se gira como se muestra.

Si el producto vectorial de dos vectores es el vector cero (es decir, a × b = 0 ), entonces una o ambas entradas son el vector cero ( a = 0 o b = 0 ) o bien son paralelas o antiparalelas ( a ∥ b ) de modo que el seno del ángulo entre ellas es cero ( θ = 0° o θ = 180° y sen  θ = 0 ).

El autoproducto vectorial de un vector es el vector cero:

${\displaystyle \mathbf {a} \times \mathbf {a} =\mathbf {0} .}$

El producto vectorial es anticonmutativo ,

${\displaystyle \mathbf {a} \times \mathbf {b} =-(\mathbf {b} \times \mathbf {a} ),}$

distributivo sobre adición,

${\displaystyle \mathbf {a} \times (\mathbf {b} +\mathbf {c} )=(\mathbf {a} \times \mathbf {b} )+(\mathbf {a} \times \mathbf {c} ),}$

y compatible con la multiplicación escalar de modo que

${\displaystyle (r\,\mathbf {a} )\times \mathbf {b} =\mathbf {a} \times (r\,\mathbf {b} )=r\,(\mathbf {a} \times \mathbf {b} ).}$

No es asociativo , pero satisface la identidad de Jacobi :

${\displaystyle \mathbf {a} \times (\mathbf {b} \times \mathbf {c} )+\mathbf {b} \times (\mathbf {c} \times \mathbf {a} )+\mathbf {c} \times (\mathbf {a} \times \mathbf {b} )=\mathbf {0} .}$

La distributividad, la linealidad y la identidad de Jacobi muestran que el espacio vectorial R ³ junto con la suma de vectores y el producto vectorial forman un álgebra de Lie , el álgebra de Lie del grupo ortogonal real en 3 dimensiones, SO(3) . El producto vectorial no obedece a la ley de cancelación ; es decir, a × b = a × c con a ≠ 0 no implica b = c , sino solo que:

${\displaystyle {\begin{aligned}\mathbf {0} &=(\mathbf {a} \times \mathbf {b} )-(\mathbf {a} \times \mathbf {c} )\\&=\mathbf {a} \times (\mathbf {b} -\mathbf {c} ).\\\end{aligned}}}$

Este puede ser el caso donde b y c se cancelan, pero además donde a y b − c son paralelos; es decir, están relacionados por un factor de escala t , lo que lleva a:

${\displaystyle \mathbf {c} =\mathbf {b} +t\,\mathbf {a} ,}$

para algún escalar t .

Si, además de a × b = a × c y a ≠ 0 como arriba, se da el caso de que a ⋅ b = a ⋅ c entonces

${\displaystyle {\begin{aligned}\mathbf {a} \times (\mathbf {b} -\mathbf {c} )&=\mathbf {0} \\\mathbf {a} \cdot (\mathbf {b} -\mathbf {c} )&=0,\end{aligned}}}$

Como b − c no puede ser simultáneamente paralela (para que el producto vectorial sea 0 ) y perpendicular (para que el producto escalar sea 0) a a , debe darse el caso de que b y c se cancelen: b = c .

Según la definición geométrica, el producto vectorial es invariante bajo rotaciones propias sobre el eje definido por a × b . En fórmulas:

${\displaystyle (R\mathbf {a} )\times (R\mathbf {b} )=R(\mathbf {a} \times \mathbf {b} )}$, donde es una matriz de rotación con . ${\displaystyle R}$ ${\displaystyle \det(R)=1}$

De manera más general, el producto vectorial obedece a la siguiente identidad bajo transformaciones matriciales :

${\displaystyle (M\mathbf {a} )\times (M\mathbf {b} )=(\det M)\left(M^{-1}\right)^{\mathrm {T} }(\mathbf {a} \times \mathbf {b} )=\operatorname {cof} M(\mathbf {a} \times \mathbf {b} )}$

donde es una matriz de 3 por 3 y es la transpuesta de la inversa y es la matriz de cofactores. Se puede ver fácilmente cómo esta fórmula se reduce a la anterior si es una matriz de rotación. Si es una matriz simétrica de 3 por 3 aplicada a un producto vectorial genérico , se cumple la siguiente relación: ${\displaystyle M}$ ${\displaystyle \left(M^{-1}\right)^{\mathrm {T} }}$ ${\displaystyle \operatorname {cof} }$ ${\displaystyle M}$ ${\displaystyle M}$ ${\displaystyle \mathbf {a} \times \mathbf {b} }$

${\displaystyle M(\mathbf {a} \times \mathbf {b} )=\operatorname {Tr} (M)(\mathbf {a} \times \mathbf {b} )-\mathbf {a} \times M\mathbf {b} +\mathbf {b} \times M\mathbf {a} }$

El producto vectorial de dos vectores se encuentra en el espacio nulo de la matriz 2 × 3 con los vectores como filas:

${\displaystyle \mathbf {a} \times \mathbf {b} \in NS\left({\begin{bmatrix}\mathbf {a} \\\mathbf {b} \end{bmatrix}}\right).}$

Para la suma de dos productos cruzados, se cumple la siguiente identidad:

${\displaystyle \mathbf {a} \times \mathbf {b} +\mathbf {c} \times \mathbf {d} =(\mathbf {a} -\mathbf {c} )\times (\mathbf {b} -\mathbf {d} )+\mathbf {a} \times \mathbf {d} +\mathbf {c} \times \mathbf {b} .}$

Diferenciación

La regla del producto del cálculo diferencial se aplica a cualquier operación bilineal y, por tanto, también al producto vectorial:

${\displaystyle {\frac {d}{dt}}(\mathbf {a} \times \mathbf {b} )={\frac {d\mathbf {a} }{dt}}\times \mathbf {b} +\mathbf {a} \times {\frac {d\mathbf {b} }{dt}},}$

donde a y b son vectores que dependen de la variable real t .

Triple expansión de productos

El producto vectorial se utiliza en ambas formas del producto triple. El producto triple escalar de tres vectores se define como

${\displaystyle \mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} ),}$

Es el volumen con signo del paralelepípedo de aristas a , b y c y, como tal, los vectores se pueden utilizar en cualquier orden que sea una permutación par del orden anterior. Por lo tanto, los siguientes son iguales:

${\displaystyle \mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} )=\mathbf {b} \cdot (\mathbf {c} \times \mathbf {a} )=\mathbf {c} \cdot (\mathbf {a} \times \mathbf {b} ),}$

El producto triple vectorial es el producto vectorial de un vector con el resultado de otro producto vectorial, y está relacionado con el producto escalar mediante la siguiente fórmula

${\displaystyle {\begin{aligned}\mathbf {a} \times (\mathbf {b} \times \mathbf {c} )=\mathbf {b} (\mathbf {a} \cdot \mathbf {c} )-\mathbf {c} (\mathbf {a} \cdot \mathbf {b} )\\(\mathbf {a} \times \mathbf {b} )\times \mathbf {c} =\mathbf {b} (\mathbf {c} \cdot \mathbf {a} )-\mathbf {a} (\mathbf {b} \cdot \mathbf {c} )\end{aligned}}}$

La regla mnemotécnica "BAC menos CAB" se utiliza para recordar el orden de los vectores en el miembro de la derecha. Esta fórmula se utiliza en física para simplificar los cálculos vectoriales. Un caso especial, relacionado con los gradientes y útil en el cálculo vectorial , es

${\displaystyle {\begin{aligned}\nabla \times (\nabla \times \mathbf {f} )&=\nabla (\nabla \cdot \mathbf {f} )-(\nabla \cdot \nabla )\mathbf {f} \\&=\nabla (\nabla \cdot \mathbf {f} )-\nabla ^{2}\mathbf {f} ,\\\end{aligned}}}$

donde ∇ ² es el operador laplaciano vectorial .

Otras identidades relacionan el producto vectorial con el triple producto escalar:

${\displaystyle {\begin{aligned}(\mathbf {a} \times \mathbf {b} )\times (\mathbf {a} \times \mathbf {c} )&=(\mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} ))\mathbf {a} \\(\mathbf {a} \times \mathbf {b} )\cdot (\mathbf {c} \times \mathbf {d} )&=\mathbf {b} ^{\mathrm {T} }\left(\left(\mathbf {c} ^{\mathrm {T} }\mathbf {a} \right)I-\mathbf {c} \mathbf {a} ^{\mathrm {T} }\right)\mathbf {d} \\&=(\mathbf {a} \cdot \mathbf {c} )(\mathbf {b} \cdot \mathbf {d} )-(\mathbf {a} \cdot \mathbf {d} )(\mathbf {b} \cdot \mathbf {c} )\end{aligned}}}$

donde I es la matriz identidad.

Formulación alternativa

El producto vectorial y el producto escalar están relacionados por:

${\displaystyle \left\|\mathbf {a} \times \mathbf {b} \right\|^{2}=\left\|\mathbf {a} \right\|^{2}\left\|\mathbf {b} \right\|^{2}-(\mathbf {a} \cdot \mathbf {b} )^{2}.}$

El lado derecho es el determinante de Gram de a y b , el cuadrado del área del paralelogramo definido por los vectores. Esta condición determina la magnitud del producto vectorial. Es decir, dado que el producto escalar se define, en términos del ángulo θ entre los dos vectores, como:

${\displaystyle \mathbf {a\cdot b} =\left\|\mathbf {a} \right\|\left\|\mathbf {b} \right\|\cos \theta ,}$

La relación dada anteriormente se puede reescribir de la siguiente manera:

${\displaystyle \left\|\mathbf {a\times b} \right\|^{2}=\left\|\mathbf {a} \right\|^{2}\left\|\mathbf {b} \right\|^{2}\left(1-\cos ^{2}\theta \right).}$

Invocando la identidad trigonométrica pitagórica se obtiene:

${\displaystyle \left\|\mathbf {a} \times \mathbf {b} \right\|=\left\|\mathbf {a} \right\|\left\|\mathbf {b} \right\|\left|\sin \theta \right|,}$

que es la magnitud del producto vectorial expresado en términos de θ , igual al área del paralelogramo definido por a y b (ver definición arriba).

La combinación de este requisito y la propiedad de que el producto vectorial sea ortogonal a sus constituyentes a y b proporciona una definición alternativa del producto vectorial. ^[13]

Producto vectorial inverso

Para el producto vectorial a × b = c , existen múltiples vectores b que dan el mismo valor de c . Como resultado, no es posible reorganizar esta ecuación para obtener una solución única para b en términos de a y c . Sin embargo, es posible encontrar una familia de soluciones para b , que son

${\displaystyle \mathbf {b} ={\frac {\mathbf {c} \times \mathbf {a} }{\left\|\mathbf {a} \right\|^{2}}}+t\mathbf {a} ,}$

donde t es una constante arbitraria.

Esto se puede derivar utilizando la expansión del triple producto:

${\displaystyle \mathbf {c} \times \mathbf {a} =(\mathbf {a} \times \mathbf {b} )\times \mathbf {a} =\left\|\mathbf {a} \right\|^{2}\mathbf {b} -(\mathbf {a} \cdot \mathbf {b} )\mathbf {a} }$

Reordenar para resolver b para obtener

${\displaystyle \mathbf {b} ={\frac {\mathbf {c} \times \mathbf {a} }{\left\|\mathbf {a} \right\|^{2}}}+{\frac {\mathbf {a} \cdot \mathbf {b} }{\left\|\mathbf {a} \right\|^{2}}}\mathbf {a} }$

El coeficiente del último término se puede simplificar a la constante arbitraria t para obtener el resultado que se muestra arriba.

La identidad de Lagrange

La relación

${\displaystyle \left\|\mathbf {a} \times \mathbf {b} \right\|^{2}\equiv \det {\begin{bmatrix}\mathbf {a} \cdot \mathbf {a} &\mathbf {a} \cdot \mathbf {b} \\\mathbf {a} \cdot \mathbf {b} &\mathbf {b} \cdot \mathbf {b} \\\end{bmatrix}}\equiv \left\|\mathbf {a} \right\|^{2}\left\|\mathbf {b} \right\|^{2}-(\mathbf {a} \cdot \mathbf {b} )^{2}}$

se puede comparar con otra relación que involucra el lado derecho, es decir, la identidad de Lagrange expresada como ^[14]

${\displaystyle \sum _{1\leq i<j\leq n}\left(a_{i}b_{j}-a_{j}b_{i}\right)^{2}\equiv \left\|\mathbf {a} \right\|^{2}\left\|\mathbf {b} \right\|^{2}-(\mathbf {a\cdot b} )^{2},}$

donde a y b pueden ser vectores n -dimensionales. Esto también muestra que la forma de volumen de Riemann para superficies es exactamente el elemento de superficie del cálculo vectorial. En el caso en que n = 3 , la combinación de estas dos ecuaciones da como resultado la expresión para la magnitud del producto vectorial en términos de sus componentes: ^[15]

${\displaystyle {\begin{aligned}\|\mathbf {a} \times \mathbf {b} \|^{2}&\equiv \sum _{1\leq i<j\leq 3}(a_{i}b_{j}-a_{j}b_{i})^{2}\\&\equiv (a_{1}b_{2}-b_{1}a_{2})^{2}+(a_{2}b_{3}-a_{3}b_{2})^{2}+(a_{3}b_{1}-a_{1}b_{3})^{2}.\end{aligned}}}$

El mismo resultado se obtiene directamente utilizando los componentes del producto vectorial obtenido a partir de

${\displaystyle \mathbf {a} \times \mathbf {b} \equiv \det {\begin{bmatrix}{\hat {\mathbf {i} }}&{\hat {\mathbf {j} }}&{\hat {\mathbf {k} }}\\a_{1}&a_{2}&a_{3}\\b_{1}&b_{2}&b_{3}\\\end{bmatrix}}.}$

En R ³ , la ecuación de Lagrange es un caso especial de la multiplicidad | vw | = | v || w | de la norma en el álgebra de cuaterniones .

Es un caso especial de otra fórmula, también llamada a veces identidad de Lagrange, que es el caso tridimensional de la identidad de Binet-Cauchy : ^{[16] [17]}

${\displaystyle (\mathbf {a} \times \mathbf {b} )\cdot (\mathbf {c} \times \mathbf {d} )\equiv (\mathbf {a} \cdot \mathbf {c} )(\mathbf {b} \cdot \mathbf {d} )-(\mathbf {a} \cdot \mathbf {d} )(\mathbf {b} \cdot \mathbf {c} ).}$

Si a = c y b = d , esto se simplifica a la fórmula anterior.

Generadores infinitesimales de rotaciones

El producto vectorial describe convenientemente los generadores infinitesimales de rotaciones en R ³ . Específicamente, si n es un vector unitario en R ³ y R ( φ ,  n ) denota una rotación sobre el eje que pasa por el origen especificado por n , con un ángulo φ (medido en radianes, en sentido antihorario cuando se ve desde la punta de n ), entonces

${\displaystyle \left.{d \over d\phi }\right|_{\phi =0}R(\phi ,{\boldsymbol {n}}){\boldsymbol {x}}={\boldsymbol {n}}\times {\boldsymbol {x}}}$

para cada vector x en R ³ . El producto vectorial con n describe, por tanto, el generador infinitesimal de las rotaciones alrededor de n . Estos generadores infinitesimales forman el álgebra de Lie so (3) del grupo de rotaciones SO(3) , y obtenemos el resultado de que el álgebra de Lie R ³ con producto vectorial es isomorfa al álgebra de Lie so (3).

Formas alternativas de calcular

Conversión a multiplicación de matrices

El producto vectorial también se puede expresar como el producto de una matriz antisimétrica y un vector: ^[16] donde el superíndice ^T se refiere a la operación de transposición , y [ a ] _​​× se define por: $${\displaystyle {\begin{aligned}\mathbf {a} \times \mathbf {b} =[\mathbf {a} ]_{\times }\mathbf {b} &={\begin{bmatrix}\,0&\!-a_{3}&\,\,a_{2}\\\,\,a_{3}&0&\!-a_{1}\\-a_{2}&\,\,a_{1}&\,0\end{bmatrix}}{\begin{bmatrix}b_{1}\\b_{2}\\b_{3}\end{bmatrix}}\\\mathbf {a} \times \mathbf {b} ={[\mathbf {b} ]_{\times }}^{\mathrm {\!\!T} }\mathbf {a} &={\begin{bmatrix}\,0&\,\,b_{3}&\!-b_{2}\\-b_{3}&0&\,\,b_{1}\\\,\,b_{2}&\!-b_{1}&\,0\end{bmatrix}}{\begin{bmatrix}a_{1}\\a_{2}\\a_{3}\end{bmatrix}},\end{aligned}}}$$ $${\displaystyle [\mathbf {a} ]_{\times }{\stackrel {\rm {def}}{=}}{\begin{bmatrix}\,\,0&\!-a_{3}&\,\,\,a_{2}\\\,\,\,a_{3}&0&\!-a_{1}\\\!-a_{2}&\,\,a_{1}&\,\,0\end{bmatrix}}.}$$

Las columnas [ a ] _​​×,i de la matriz antisimétrica para un vector a también se pueden obtener calculando el producto vectorial con los vectores unitarios . Es decir, o donde es el operador de producto externo . $${\displaystyle [\mathbf {a} ]_{\times ,i}=\mathbf {a} \times \mathbf {{\hat {e}}_{i}} ,\;i\in \{1,2,3\}}$$ $${\displaystyle [\mathbf {a} ]_{\times }=\sum _{i=1}^{3}\left(\mathbf {a} \times \mathbf {{\hat {e}}_{i}} \right)\otimes \mathbf {{\hat {e}}_{i}} ,}$$ ${\displaystyle \otimes }$

Además, si a se expresa como un producto vectorial: entonces $${\displaystyle \mathbf {a} =\mathbf {c} \times \mathbf {d} }$$ $${\displaystyle [\mathbf {a} ]_{\times }=\mathbf {d} \mathbf {c} ^{\mathrm {T} }-\mathbf {c} \mathbf {d} ^{\mathrm {T} }.}$$

Prueba por sustitución

La evaluación del producto vectorial da Por lo tanto, el lado izquierdo es igual Ahora, para el lado derecho, Y su transpuesta es La evaluación del lado derecho da La comparación muestra que el lado izquierdo es igual al lado derecho. $${\displaystyle \mathbf {a} =\mathbf {c} \times \mathbf {d} ={\begin{pmatrix}c_{2}d_{3}-c_{3}d_{2}\\c_{3}d_{1}-c_{1}d_{3}\\c_{1}d_{2}-c_{2}d_{1}\end{pmatrix}}}$$ $${\displaystyle [\mathbf {a} ]_{\times }={\begin{bmatrix}0&c_{2}d_{1}-c_{1}d_{2}&c_{3}d_{1}-c_{1}d_{3}\\c_{1}d_{2}-c_{2}d_{1}&0&c_{3}d_{2}-c_{2}d_{3}\\c_{1}d_{3}-c_{3}d_{1}&c_{2}d_{3}-c_{3}d_{2}&0\end{bmatrix}}}$$ $${\displaystyle \mathbf {c} \mathbf {d} ^{\mathrm {T} }={\begin{bmatrix}c_{1}d_{1}&c_{1}d_{2}&c_{1}d_{3}\\c_{2}d_{1}&c_{2}d_{2}&c_{2}d_{3}\\c_{3}d_{1}&c_{3}d_{2}&c_{3}d_{3}\end{bmatrix}}}$$ $${\displaystyle \mathbf {d} \mathbf {c} ^{\mathrm {T} }={\begin{bmatrix}c_{1}d_{1}&c_{2}d_{1}&c_{3}d_{1}\\c_{1}d_{2}&c_{2}d_{2}&c_{3}d_{2}\\c_{1}d_{3}&c_{2}d_{3}&c_{3}d_{3}\end{bmatrix}}}$$ $${\displaystyle \mathbf {d} \mathbf {c} ^{\mathrm {T} }-\mathbf {c} \mathbf {d} ^{\mathrm {T} }={\begin{bmatrix}0&c_{2}d_{1}-c_{1}d_{2}&c_{3}d_{1}-c_{1}d_{3}\\c_{1}d_{2}-c_{2}d_{1}&0&c_{3}d_{2}-c_{2}d_{3}\\c_{1}d_{3}-c_{3}d_{1}&c_{2}d_{3}-c_{3}d_{2}&0\end{bmatrix}}}$$

Este resultado se puede generalizar a dimensiones superiores utilizando álgebra geométrica . En particular, en cualquier dimensión los bivectores se pueden identificar con matrices antisimétricas, por lo que el producto entre una matriz antisimétrica y un vector es equivalente a la parte de grado 1 del producto de un bivector y un vector. ^[18] En tres dimensiones, los bivectores son duales de los vectores, por lo que el producto es equivalente al producto vectorial, con el bivector en lugar de su vector dual. En dimensiones superiores, el producto aún se puede calcular, pero los bivectores tienen más grados de libertad y no son equivalentes a los vectores. ^[18]

Esta notación también suele ser mucho más fácil de utilizar, por ejemplo, en geometría epipolar .

De las propiedades generales del producto vectorial se deduce inmediatamente que   y   y del hecho de que [ a ] _​​× es antisimétrico se deduce que $${\displaystyle [\mathbf {a} ]_{\times }\,\mathbf {a} =\mathbf {0} }$$ $${\displaystyle \mathbf {a} ^{\mathrm {T} }\,[\mathbf {a} ]_{\times }=\mathbf {0} }$$ $${\displaystyle \mathbf {b} ^{\mathrm {T} }\,[\mathbf {a} ]_{\times }\,\mathbf {b} =0.}$$

La expansión del triple producto mencionada anteriormente (regla bac-cab) se puede demostrar fácilmente utilizando esta notación.

Como se mencionó anteriormente, el álgebra de Lie R ³ con producto vectorial es isomorfa al álgebra de Lie so(3) , cuyos elementos pueden identificarse con las matrices antisimétricas 3×3. La función a → [ a ] _​​× proporciona un isomorfismo entre R ³ y so(3) . Bajo esta función, el producto vectorial de 3-vectores corresponde al conmutador de matrices antisimétricas 3x3.

Notación de índice para tensores

El producto vectorial se puede definir alternativamente en términos del tensor de Levi-Civita E _ijk y un producto escalar η ^mi , que son útiles para convertir la notación vectorial para aplicaciones tensoriales:

${\displaystyle \mathbf {c} =\mathbf {a\times b} \Leftrightarrow \ c^{m}=\sum _{i=1}^{3}\sum _{j=1}^{3}\sum _{k=1}^{3}\eta ^{mi}E_{ijk}a^{j}b^{k}}$

donde los índices corresponden a los componentes del vector. Esta caracterización del producto vectorial se expresa a menudo de forma más compacta utilizando la convención de suma de Einstein como ${\displaystyle i,j,k}$

${\displaystyle \mathbf {c} =\mathbf {a\times b} \Leftrightarrow \ c^{m}=\eta ^{mi}E_{ijk}a^{j}b^{k}}$

en el que los índices repetidos se suman sobre los valores 1 a 3.

En una base ortonormal orientada positivamente η ^mi = δ ^mi (el delta de Kronecker ) y (el símbolo de Levi-Civita ). En ese caso, esta representación es otra forma de la representación antisimétrica del producto vectorial: ${\displaystyle E_{ijk}=\varepsilon _{ijk}}$

${\displaystyle [\varepsilon _{ijk}a^{j}]=[\mathbf {a} ]_{\times }.}$

En mecánica clásica : la representación del producto vectorial mediante el símbolo de Levi-Civita puede hacer que las simetrías mecánicas sean obvias cuando los sistemas físicos son isótropos . (Un ejemplo: considere una partícula en un potencial de la Ley de Hooke en un espacio tridimensional, libre de oscilar en tres dimensiones; ninguna de estas dimensiones es "especial" en ningún sentido, por lo que las simetrías se encuentran en el momento angular representado por el producto vectorial, que se aclara mediante la representación de Levi-Civita mencionada anteriormente). ^{[ cita requerida ]}

Mnemotécnico

Mnemónico para calcular un producto vectorial

La palabra "xyzzy" se puede utilizar para recordar la definición del producto vectorial.

Si

${\displaystyle \mathbf {a} =\mathbf {b} \times \mathbf {c} }$

dónde:

${\displaystyle \mathbf {a} ={\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\end{bmatrix}},\ \mathbf {b} ={\begin{bmatrix}b_{x}\\b_{y}\\b_{z}\end{bmatrix}},\ \mathbf {c} ={\begin{bmatrix}c_{x}\\c_{y}\\c_{z}\end{bmatrix}}}$

entonces:

${\displaystyle a_{x}=b_{y}c_{z}-b_{z}c_{y}}$

${\displaystyle a_{y}=b_{z}c_{x}-b_{x}c_{z}}$

${\displaystyle a_{z}=b_{x}c_{y}-b_{y}c_{x}.}$

La segunda y tercera ecuaciones se pueden obtener a partir de la primera simplemente rotando verticalmente los subíndices, x → y → z → x . El problema, por supuesto, es cómo recordar la primera ecuación, y hay dos opciones disponibles para este propósito: o bien recordar las dos diagonales relevantes del esquema de Sarrus (las que contienen i ), o bien recordar la secuencia xyzzy.

Dado que la primera diagonal del esquema de Sarrus es simplemente la diagonal principal de la matriz 3×3 mencionada anteriormente, las primeras tres letras de la palabra xyzzy se pueden recordar muy fácilmente.

Visualización cruzada

De manera similar al recurso mnemotécnico anterior, se puede visualizar una "cruz" o X entre los dos vectores de la ecuación. Esto puede resultar útil para recordar la fórmula correcta del producto vectorial.

Si

${\displaystyle \mathbf {a} =\mathbf {b} \times \mathbf {c} }$

entonces:

${\displaystyle \mathbf {a} ={\begin{bmatrix}b_{x}\\b_{y}\\b_{z}\end{bmatrix}}\times {\begin{bmatrix}c_{x}\\c_{y}\\c_{z}\end{bmatrix}}.}$

Si queremos obtener la fórmula, simplemente eliminamos el y de la fórmula y quitamos los dos componentes siguientes: ${\displaystyle a_{x}}$ ${\displaystyle b_{x}}$ ${\displaystyle c_{x}}$

${\displaystyle a_{x}={\begin{bmatrix}b_{y}\\b_{z}\end{bmatrix}}\times {\begin{bmatrix}c_{y}\\c_{z}\end{bmatrix}}.}$

Al hacer esto para los dos elementos siguientes hacia abajo se debe "envolver" la matriz de modo que después del componente z venga el componente x. Para mayor claridad, al realizar esta operación para , los dos componentes siguientes deben ser z y x (en ese orden). Mientras que para los dos componentes siguientes se deben tomar como x e y. ${\displaystyle a_{y}}$ ${\displaystyle a_{y}}$ ${\displaystyle a_{z}}$

${\displaystyle a_{y}={\begin{bmatrix}b_{z}\\b_{x}\end{bmatrix}}\times {\begin{bmatrix}c_{z}\\c_{x}\end{bmatrix}},\ a_{z}={\begin{bmatrix}b_{x}\\b_{y}\end{bmatrix}}\times {\begin{bmatrix}c_{x}\\c_{y}\end{bmatrix}}}$

Entonces , si visualizamos el operador cruz como si apuntara de un elemento de la izquierda a un elemento de la derecha, podemos tomar el primer elemento de la izquierda y simplemente multiplicarlo por el elemento al que apunta la cruz en la matriz de la derecha. Luego restamos el siguiente elemento hacia abajo a la izquierda, multiplicado por el elemento al que apunta la cruz aquí también. Esto da como resultado nuestra fórmula: ${\displaystyle a_{x}}$ ${\displaystyle a_{x}}$

${\displaystyle a_{x}=b_{y}c_{z}-b_{z}c_{y}.}$

Podemos hacer esto de la misma manera para y para construir sus fórmulas asociadas. ${\displaystyle a_{y}}$ ${\displaystyle a_{z}}$

Aplicaciones

El producto vectorial tiene aplicaciones en diversos contextos. Por ejemplo, se utiliza en geometría computacional, física e ingeniería. A continuación se presenta una lista no exhaustiva de ejemplos.

Geometría computacional

El producto vectorial aparece en el cálculo de la distancia de dos líneas oblicuas (líneas que no están en el mismo plano) entre sí en el espacio tridimensional.

El producto vectorial se puede utilizar para calcular la normal de un triángulo o polígono, una operación que se realiza con frecuencia en gráficos por computadora . Por ejemplo, el giro de un polígono (en el sentido de las agujas del reloj o en sentido contrario) alrededor de un punto dentro del polígono se puede calcular triangulando el polígono (como si se tratara de los radios de una rueda) y sumando los ángulos (entre los radios) utilizando el producto vectorial para llevar un registro del signo de cada ángulo.

En geometría computacional del plano , el producto vectorial se utiliza para determinar el signo del ángulo agudo definido por tres puntos y . Corresponde a la dirección (hacia arriba o hacia abajo) del producto vectorial de los dos vectores coplanares definidos por los dos pares de puntos y . El signo del ángulo agudo es el signo de la expresión ${\displaystyle p_{1}=(x_{1},y_{1}),p_{2}=(x_{2},y_{2})}$ ${\displaystyle p_{3}=(x_{3},y_{3})}$ ${\displaystyle (p_{1},p_{2})}$ ${\displaystyle (p_{1},p_{3})}$

${\displaystyle P=(x_{2}-x_{1})(y_{3}-y_{1})-(y_{2}-y_{1})(x_{3}-x_{1}),}$

que es la longitud con signo del producto vectorial de los dos vectores.

En el sistema de coordenadas "diestro", si el resultado es 0, los puntos son colineales ; si es positivo, los tres puntos forman un ángulo de rotación positivo alrededor de a , en caso contrario un ángulo negativo. Desde otro punto de vista, el signo de indica si se encuentra a la izquierda o a la derecha de la recta. ${\displaystyle p_{1}}$ ${\displaystyle p_{2}}$ ${\displaystyle p_{3}}$ ${\displaystyle P}$ ${\displaystyle p_{3}}$ ${\displaystyle p_{1},p_{2}.}$

El producto vectorial se utiliza para calcular el volumen de un poliedro, como un tetraedro o un paralelepípedo .

Momento angular y par

El momento angular L de una partícula alrededor de un origen dado se define como:

${\displaystyle \mathbf {L} =\mathbf {r} \times \mathbf {p} ,}$

donde r es el vector de posición de la partícula con respecto al origen, p es el momento lineal de la partícula.

De la misma manera, el momento M de una fuerza F _B aplicada en el punto B alrededor del punto A se da como:

${\displaystyle \mathbf {M} _{\mathrm {A} }=\mathbf {r} _{\mathrm {AB} }\times \mathbf {F} _{\mathrm {B} }\,}$

En mecánica, el momento de una fuerza también se llama torque y se escribe como ${\displaystyle \mathbf {\tau } }$

Dado que la posición r , el momento lineal p y la fuerza F son todos vectores verdaderos , tanto el momento angular L como el momento de una fuerza M son pseudovectores o vectores axiales .

Cuerpo rígido

El producto vectorial aparece con frecuencia en la descripción de movimientos rígidos. Dos puntos P y Q de un cuerpo rígido pueden relacionarse mediante:

${\displaystyle \mathbf {v} _{P}-\mathbf {v} _{Q}={\boldsymbol {\omega }}\times \left(\mathbf {r} _{P}-\mathbf {r} _{Q}\right)\,}$

donde es la posición del punto, es su velocidad y es la velocidad angular del cuerpo . ${\displaystyle \mathbf {r} }$ ${\displaystyle \mathbf {v} }$ ${\displaystyle {\boldsymbol {\omega }}}$

Como la posición y la velocidad son vectores verdaderos , la velocidad angular es un pseudovector o vector axial . ${\displaystyle \mathbf {r} }$ ${\displaystyle \mathbf {v} }$ ${\displaystyle {\boldsymbol {\omega }}}$

Fuerza de Lorentz

El producto vectorial se utiliza para describir la fuerza de Lorentz que experimenta una carga eléctrica en movimiento q _e :

${\displaystyle \mathbf {F} =q_{e}\left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right)}$

Como la velocidad v , la fuerza F y el campo eléctrico E son todos vectores verdaderos , el campo magnético B es un pseudovector .

Otro

En el cálculo vectorial , el producto vectorial se utiliza para definir la fórmula del operador vectorial curl .

El truco de reescribir un producto vectorial en términos de una multiplicación de matrices aparece con frecuencia en geometría epipolar y de múltiples vistas, en particular al derivar restricciones de coincidencia.

Como producto externo

El producto vectorial en relación con el producto exterior. En rojo se muestran el vector unitario ortogonal y el bivector unitario "paralelo".

El producto vectorial puede definirse en términos del producto exterior. Puede generalizarse a un producto exterior en dimensiones distintas a las tres. ^[19] Esta generalización permite una interpretación geométrica natural del producto vectorial. En álgebra exterior , el producto exterior de dos vectores es un bivector. Un bivector es un elemento plano orientado, de la misma manera que un vector es un elemento lineal orientado. Dados dos vectores a y b , se puede ver el bivector a ∧ b como el paralelogramo orientado generado por a y b . El producto vectorial se obtiene entonces tomando la estrella de Hodge del bivector a ∧ b , convirtiendo los 2-vectores en vectores:

${\displaystyle a\times b=\star (a\wedge b).}$

Esto puede considerarse como el elemento multidimensional orientado "perpendicular" al bivector. En un espacio de dimensión d , la estrella de Hodge convierte un vector k en un vector ( d–k ); por lo tanto, solo en d = 3 dimensiones el resultado es un elemento de dimensión uno (3–2 = 1), es decir, un vector. Por ejemplo, en d = 4 dimensiones, el producto vectorial de dos vectores tiene dimensión 4–2 = 2, lo que da un bivector. Por lo tanto, solo en tres dimensiones el producto vectorial define una estructura algebraica para multiplicar vectores.

Lateralidad

Consistencia

Cuando las leyes de la física se escriben como ecuaciones, es posible hacer una elección arbitraria del sistema de coordenadas, incluida la lateralidad. Se debe tener cuidado de nunca escribir una ecuación en la que los dos lados no se comporten de la misma manera bajo todas las transformaciones que deben considerarse. Por ejemplo, si un lado de la ecuación es un producto vectorial de dos vectores polares , se debe tener en cuenta que el resultado es un vector axial . Por lo tanto, por coherencia, el otro lado también debe ser un vector axial. ^{[ cita requerida ]} De manera más general, el resultado de un producto vectorial puede ser un vector polar o un vector axial, dependiendo del tipo de sus operandos (vectores polares o vectores axiales). Es decir, los vectores polares y los vectores axiales están interrelacionados de las siguientes maneras bajo la aplicación del producto vectorial:

• vector polar × vector polar = vector axial
• vector axial × vector axial = vector axial
• vector polar × vector axial = vector polar
• vector axial × vector polar = vector polar

o simbólicamente

• polar × polar = axial
• axial × axial = axial
• polar × axial = polar
• axial × polar = polar

Como el producto vectorial también puede ser un vector polar, no puede cambiar de dirección con una transformación de imagen especular. Esto sucede, según las relaciones anteriores, si uno de los operandos es un vector polar y el otro es un vector axial (por ejemplo, el producto vectorial de dos vectores polares). Por ejemplo, un producto triple de vectores que involucra tres vectores polares es un vector polar.

Es posible adoptar un enfoque sin lateralidad utilizando álgebra exterior.

La paradoja de la base ortonormal

Sea ( i , j , k ) una base ortonormal. Los vectores i , j y k no dependen de la orientación del espacio. Pueden definirse incluso en ausencia de orientación alguna. Por lo tanto, no pueden ser vectores axiales. Pero si i y j son vectores polares, entonces k es un vector axial para i × j = k o j × i = k . Esto es una paradoja.

"Axial" y "polar" son calificativos físicos de vectores físicos ; es decir, vectores que representan magnitudes físicas como la velocidad o el campo magnético. Los vectores i , j y k son vectores matemáticos, ni axiales ni polares. En matemáticas, el producto vectorial de dos vectores es un vector. No hay contradicción.

Generalizaciones

Hay varias formas de generalizar el producto vectorial a dimensiones superiores.

Álgebra de Lie

El producto vectorial puede considerarse uno de los productos de Lie más simples y, por lo tanto, se generaliza mediante álgebras de Lie , que se axiomatizan como productos binarios que satisfacen los axiomas de multilinealidad, simetría antisimétrica e identidad de Jacobi. Existen muchas álgebras de Lie y su estudio es un campo importante de las matemáticas, llamado teoría de Lie .

Por ejemplo, el álgebra de Heisenberg da otra estructura de álgebra de Lie en la que el producto es ${\displaystyle \mathbf {R} ^{3}.}$ ${\displaystyle \{x,y,z\},}$ ${\displaystyle [x,y]=z,[x,z]=[y,z]=0.}$

Cuaterniones

El producto vectorial también se puede describir en términos de cuaterniones . En general, si un vector [ a ₁ , a ₂ , a ₃ ] se representa como el cuaternión a ₁ i + a ₂ j + a ₃ k , el producto vectorial de dos vectores se puede obtener tomando su producto como cuaterniones y eliminando la parte real del resultado. La parte real será el negativo del producto escalar de los dos vectores.

Octoniones

Se puede obtener un producto vectorial de vectores de siete dimensiones de la misma manera, utilizando octoniones en lugar de cuaterniones. La inexistencia de productos vectoriales no triviales de dos vectores en otras dimensiones está relacionada con el resultado del teorema de Hurwitz de que las únicas álgebras de división normadas son aquellas con dimensión 1, 2, 4 y 8.

Producto exterior

En la dimensión general, no existe un análogo directo del producto vectorial binario que produzca específicamente un vector. Sin embargo, existe el producto exterior, que tiene propiedades similares, excepto que el producto exterior de dos vectores es ahora un 2-vector en lugar de un vector ordinario. Como se mencionó anteriormente, el producto vectorial se puede interpretar como el producto exterior en tres dimensiones utilizando el operador de estrella de Hodge para convertir los 2-vectores en vectores. El dual de Hodge del producto exterior produce un ( n − 2) -vector, que es una generalización natural del producto vectorial en cualquier número de dimensiones.

El producto exterior y el producto escalar se pueden combinar (mediante la suma) para formar el producto geométrico en álgebra geométrica.

Producto externo

Como se mencionó anteriormente, el producto vectorial puede interpretarse en tres dimensiones como el dual de Hodge del producto exterior. En cualquier dimensión finita n , el dual de Hodge del producto exterior de n − 1 vectores es un vector. Por lo tanto, en lugar de una operación binaria, en dimensiones finitas arbitrarias, el producto vectorial se generaliza como el dual de Hodge del producto exterior de algunos n − 1 vectores dados. Esta generalización se llama producto externo . ^[20]

Producto conmutador

Interpretando el espacio vectorial tridimensional del álgebra como la subálgebra de 2 vectores (no de 1 vector) del álgebra geométrica tridimensional, donde , , y , el producto vectorial corresponde exactamente al producto conmutador en álgebra geométrica y ambos utilizan el mismo símbolo . El producto conmutador se define para 2 vectores y en álgebra geométrica como: ${\displaystyle \mathbf {i} =\mathbf {e_{2}} \mathbf {e_{3}} }$ ${\displaystyle \mathbf {j} =\mathbf {e_{1}} \mathbf {e_{3}} }$ ${\displaystyle \mathbf {k} =\mathbf {e_{1}} \mathbf {e_{2}} }$ ${\displaystyle \times }$ ${\displaystyle A}$ ${\displaystyle B}$

${\displaystyle A\times B={\tfrac {1}{2}}(AB-BA),}$

donde es el producto geométrico. ^[21] ${\displaystyle AB}$

The commutator product could be generalised to arbitrary multivectors in three dimensions, which results in a multivector consisting of only elements of grades 1 (1-vectors/true vectors) and 2 (2-vectors/pseudovectors). While the commutator product of two 1-vectors is indeed the same as the exterior product and yields a 2-vector, the commutator of a 1-vector and a 2-vector yields a true vector, corresponding instead to the left and right contractions in geometric algebra. The commutator product of two 2-vectors has no corresponding equivalent product, which is why the commutator product is defined in the first place for 2-vectors. Furthermore, the commutator triple product of three 2-vectors is the same as the vector triple product of the same three pseudovectors in vector algebra. However, the commutator triple product of three 1-vectors in geometric algebra is instead the negative of the vector triple product of the same three true vectors in vector algebra.

Generalizations to higher dimensions is provided by the same commutator product of 2-vectors in higher-dimensional geometric algebras, but the 2-vectors are no longer pseudovectors. Just as the commutator product/cross product of 2-vectors in three dimensions correspond to the simplest Lie algebra, the 2-vector subalgebras of higher dimensional geometric algebra equipped with the commutator product also correspond to the Lie algebras.^[22] Also as in three dimensions, the commutator product could be further generalised to arbitrary multivectors.

Multilinear algebra

In the context of multilinear algebra, the cross product can be seen as the (1,2)-tensor (a mixed tensor, specifically a bilinear map) obtained from the 3-dimensional volume form,^{[note 2]} a (0,3)-tensor, by raising an index.

In detail, the 3-dimensional volume form defines a product ${\displaystyle V\times V\times V\to \mathbf {R} ,}$ by taking the determinant of the matrix given by these 3 vectors. By duality, this is equivalent to a function ${\displaystyle V\times V\to V^{*},}$ (fixing any two inputs gives a function ${\displaystyle V\to \mathbf {R} }$ by evaluating on the third input) and in the presence of an inner product (such as the dot product; more generally, a non-degenerate bilinear form), we have an isomorphism ${\displaystyle V\to V^{*},}$ and thus this yields a map ${\displaystyle V\times V\to V,}$ which is the cross product: a (0,3)-tensor (3 vector inputs, scalar output) has been transformed into a (1,2)-tensor (2 vector inputs, 1 vector output) by "raising an index".

Translating the above algebra into geometry, the function "volume of the parallelepiped defined by ${\displaystyle (a,b,-)}$" (where the first two vectors are fixed and the last is an input), which defines a function ${\displaystyle V\to \mathbf {R} }$, can be represented uniquely as the dot product with a vector: this vector is the cross product ${\displaystyle a\times b.}$ From this perspective, the cross product is defined by the scalar triple product, ${\displaystyle \mathrm {Vol} (a,b,c)=(a\times b)\cdot c.}$

In the same way, in higher dimensions one may define generalized cross products by raising indices of the n-dimensional volume form, which is a ${\displaystyle (0,n)}$-tensor. The most direct generalizations of the cross product are to define either:

• a ${\displaystyle (1,n-1)}$-tensor, which takes as input ${\displaystyle n-1}$ vectors, and gives as output 1 vector – an ${\displaystyle (n-1)}$-ary vector-valued product, or
• a ${\displaystyle (n-2,2)}$-tensor, which takes as input 2 vectors and gives as output skew-symmetric tensor of rank n − 2 – a binary product with rank n − 2 tensor values. One can also define ${\displaystyle (k,n-k)}$-tensors for other k.

These products are all multilinear and skew-symmetric, and can be defined in terms of the determinant and parity.

The ${\displaystyle (n-1)}$-ary product can be described as follows: given ${\displaystyle n-1}$ vectors ${\displaystyle v_{1},\dots ,v_{n-1}}$ in ${\displaystyle \mathbf {R} ^{n},}$ define their generalized cross product ${\displaystyle v_{n}=v_{1}\times \cdots \times v_{n-1}}$ as:

• perpendicular to the hyperplane defined by the ${\displaystyle v_{i},}$
• magnitude is the volume of the parallelotope defined by the ${\displaystyle v_{i},}$ which can be computed as the Gram determinant of the ${\displaystyle v_{i},}$
• oriented so that ${\displaystyle v_{1},\dots ,v_{n}}$ is positively oriented.

This is the unique multilinear, alternating product which evaluates to ${\displaystyle e_{1}\times \cdots \times e_{n-1}=e_{n}}$, ${\displaystyle e_{2}\times \cdots \times e_{n}=e_{1},}$ and so forth for cyclic permutations of indices.

In coordinates, one can give a formula for this ${\displaystyle (n-1)}$-ary analogue of the cross product in Rⁿ by:

${\displaystyle \bigwedge _{i=0}^{n-1}\mathbf {v} _{i}={\begin{vmatrix}v_{1}{}^{1}&\cdots &v_{1}{}^{n}\\\vdots &\ddots &\vdots \\v_{n-1}{}^{1}&\cdots &v_{n-1}{}^{n}\\\mathbf {e} _{1}&\cdots &\mathbf {e} _{n}\end{vmatrix}}.}$

This formula is identical in structure to the determinant formula for the normal cross product in R³ except that the row of basis vectors is the last row in the determinant rather than the first. The reason for this is to ensure that the ordered vectors (v₁, ..., v_n−1, Λ^n–1
_i=0v_i) have a positive orientation with respect to (e₁, ..., e_n). If n is odd, this modification leaves the value unchanged, so this convention agrees with the normal definition of the binary product. In the case that n is even, however, the distinction must be kept. This ${\displaystyle (n-1)}$-ary form enjoys many of the same properties as the vector cross product: it is alternating and linear in its arguments, it is perpendicular to each argument, and its magnitude gives the hypervolume of the region bounded by the arguments. And just like the vector cross product, it can be defined in a coordinate independent way as the Hodge dual of the wedge product of the arguments. Moreover, the product ${\displaystyle [v_{1},\ldots ,v_{n}]:=\bigwedge _{i=0}^{n}v_{i}}$ satisfies the Filippov identity,

${\displaystyle [[x_{1},\ldots ,x_{n}],y_{2},\ldots ,y_{n}]]=\sum _{i=1}^{n}[x_{1},\ldots ,x_{i-1},[x_{i},y_{2},\ldots ,y_{n}],x_{i+1},\ldots ,x_{n}],}$

and so it endows Rⁿ⁺¹ with a structure of n-Lie algebra (see Proposition 1 of ^[23]).

History

In 1773, Joseph-Louis Lagrange used the component form of both the dot and cross products in order to study the tetrahedron in three dimensions.^{[24][note 3]}

In 1843, William Rowan Hamilton introduced the quaternion product, and with it the terms vector and scalar. Given two quaternions [0, u] and [0, v], where u and v are vectors in R³, their quaternion product can be summarized as [−u ⋅ v, u × v]. James Clerk Maxwell used Hamilton's quaternion tools to develop his famous electromagnetism equations, and for this and other reasons quaternions for a time were an essential part of physics education.

In 1844, Hermann Grassmann published a geometric algebra not tied to dimension two or three. Grassmann developed several products, including a cross product represented then by [uv].^[25] (See also: exterior algebra.)

In 1853, Augustin-Louis Cauchy, a contemporary of Grassmann, published a paper on algebraic keys which were used to solve equations and had the same multiplication properties as the cross product.^[26][27]

In 1878, William Kingdon Clifford, known for a precursor to the Clifford algebra named in his honor, published Elements of Dynamic, in which the term vector product is attested. In the book, this product of two vectors is defined to have magnitude equal to the area of the parallelogram of which they are two sides, and direction perpendicular to their plane.^[28]

In lecture notes from 1881, Gibbs represented the cross product by ${\displaystyle u\times v}$ and called it the skew product.^[29][30] In 1901, Gibb's student Edwin Bidwell Wilson edited and extended these lecture notes into the textbook Vector Analysis. Wilson kept the term skew product, but observed that the alternative terms cross product^{[note 4]} and vector product were more frequent.^[31]

In 1908, Cesare Burali-Forti and Roberto Marcolongo introduced the vector product notation u ∧ v.^[25] This is used in France and other areas until this day, as the symbol ${\displaystyle \times }$ is already used to denote multiplication and the Cartesian product.^{[citation needed]}

See also

• Cartesian product – a product of two sets
• Geometric algebra: Rotating systems
• Multiple cross products – products involving more than three vectors
• Multiplication of vectors
• Quadruple product
• × (the symbol)

Notes

1. Here, "formal" means that this notation has the form of a determinant, but does not strictly adhere to the definition; it is a mnemonic used to remember the expansion of the cross product.
2. By a volume form one means a function that takes in n vectors and gives out a scalar, the volume of the parallelotope defined by the vectors: ${\displaystyle V\times \cdots \times V\to \mathbf {R} .}$ This is an n-ary multilinear skew-symmetric form. In the presence of a basis, such as on ${\displaystyle \mathbf {R} ^{n},}$ this is given by the determinant, but in an abstract vector space, this is added structure. In terms of G-structures, a volume form is an ${\displaystyle SL}$-structure.
3. In modern notation, Lagrange defines ${\displaystyle \mathbf {\xi } =\mathbf {y} \times \mathbf {z} }$, ${\displaystyle {\boldsymbol {\eta }}=\mathbf {z} \times \mathbf {x} }$, and ${\displaystyle {\boldsymbol {\zeta }}=\mathbf {x} \times {\boldsymbol {y}}}$. Thereby, the modern ${\displaystyle \mathbf {x} }$ corresponds to the three variables ${\displaystyle (x,x',x'')}$ in Lagrange's notation.
4. since A × B is read as "A cross B"

References

1. Weisstein, Eric W. "Cross Product". Wolfram MathWorld. Retrieved 2020-09-06.
2. "Cross Product". www.mathsisfun.com. Retrieved 2020-09-06.
3. Massey, William S. (December 1983). "Cross products of vectors in higher dimensional Euclidean spaces" (PDF). The American Mathematical Monthly. 90 (10): 697–701. doi:10.2307/2323537. JSTOR 2323537. S2CID 43318100. Archived from the original (PDF) on 2021-02-26. If one requires only three basic properties of the cross product ... it turns out that a cross product of vectors exists only in 3-dimensional and 7-dimensional Euclidean space.
4. Arfken, George B. Mathematical Methods for Physicists (4th ed.). Elsevier.
5. Jeffreys, H.; Jeffreys, B. S. (1999). Methods of mathematical physics. Cambridge University Press. OCLC 41158050.
6. Acheson, D. J. (1990). Elementary Fluid Dynamics. Oxford University Press. ISBN 0198596790.
7. Howison, Sam (2005). Practical Applied Mathematics. Cambridge University Press. ISBN 0521842743.
8. Wilson 1901, p. 60–61.
9. Dennis G. Zill; Michael R. Cullen (2006). "Definition 7.4: Cross product of two vectors". Advanced engineering mathematics (3rd ed.). Jones & Bartlett Learning. p. 324. ISBN 0-7637-4591-X.
10. Edwin Bidwell Wilson (1913). "Chapter II. Direct and Skew Products of Vectors". Vector Analysis. Founded upon the lectures of J. William Gibbs. New Haven: Yale University Press. The dot product is called "direct product", and cross product is called "skew product".
11. A History of Vector Analysis by Michael J. Crowe, Math. UC Davis.
12. M. R. Spiegel; S. Lipschutz; D. Spellman (2009). Vector Analysis. Schaum's outlines. McGraw Hill. p. 29. ISBN 978-0-07-161545-7.
13. WS Massey (Dec 1983). "Cross products of vectors in higher dimensional Euclidean spaces". The American Mathematical Monthly. 90 (10). The American Mathematical Monthly, Vol. 90, No. 10: 697–701. doi:10.2307/2323537. JSTOR 2323537.
14. Vladimir A. Boichenko; Gennadiĭ Alekseevich Leonov; Volker Reitmann (2005). Dimension theory for ordinary differential equations. Vieweg+Teubner Verlag. p. 26. ISBN 3-519-00437-2.
15. Pertti Lounesto (2001). Clifford algebras and spinors (2nd ed.). Cambridge University Press. p. 94. ISBN 0-521-00551-5.
16. Shuangzhe Liu; Gõtz Trenkler (2008). "Hadamard, Khatri-Rao, Kronecker and other matrix products". Int J Information and Systems Sciences. 4 (1). Institute for scientific computing and education: 160–177.
17. by Eric W. Weisstein (2003). "Binet-Cauchy identity". CRC concise encyclopedia of mathematics (2nd ed.). CRC Press. p. 228. ISBN 1-58488-347-2.
18. Lounesto, Pertti (2001). Clifford algebras and spinors. Cambridge: Cambridge University Press. pp. 193. ISBN 978-0-521-00551-7.
19. Greub, W. (1978). Multilinear Algebra.
20. Hogben, L, ed. (2007). Handbook of Linear Algebra.^{[page needed]}
21. Arthur, John W. (2011). Understanding Geometric Algebra for Electromagnetic Theory. IEEE Press. p. 49. ISBN 978-0470941638.
22. Doran, Chris; Lasenby, Anthony (2003). Geometric Algebra for Physicists. Cambridge University Press. pp. 401–408. ISBN 978-0521715959.
23. Filippov, V.T. (1985). "n-Lie algebras". Sibirsk. Mat. Zh. 26 (6): 879–891. doi:10.1007/BF00969110. S2CID 125051596.
24. Lagrange, Joseph-Louis (1773). "Solutions analytiques de quelques problèmes sur les pyramides triangulaires". Oeuvres. Vol. 3. p. 661.
25. Cajori (1929), p. 134.
26. Crowe (1994), p. 83.
27. Cauchy, Augustin-Louis (1900). Ouvres. Vol. 12. p. 16.
28. Clifford, William Kingdon (1878). "Elements of Dynamic, Part I". London: MacMillan & Co. p. 95.
29. Gibbs, Josiah Willard (1884). Elements of vector analysis : arranged for the use of students in physics. New Haven : Printed by Tuttle, Morehouse & Taylor.
30. Crowe (1994), p. 154.
31. Wilson (1901), p. 61.

Bibliography

• Cajori, Florian (1929). A History Of Mathematical Notations Volume II. Open Court Publishing. p. 134. ISBN 978-0-486-67766-8.
• Crowe, Michael J. (1994). A History of Vector Analysis. Dover. ISBN 0-486-67910-1.
• EA Milne (1948) Mecánica vectorial , Capítulo 2: Producto vectorial, págs. 11-31, Londres: Methuen Publishing .
• Wilson, Edwin Bidwell (1901). Análisis vectorial: libro de texto para estudiantes de matemáticas y física, basado en las conferencias de J. Willard Gibbs. Yale University Press .
• T. Levi-Civita; U. Amaldi (1949). Lezioni di meccanica razionale (en italiano). Bolonia: Zanichelli editore.

Enlaces externos

• "Producto vectorial", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
• Una rápida derivación geométrica e interpretación de productos cruzados
• Un tutorial interactivo creado en la Universidad de Syracuse (requiere Java )
• W. Kahan (2007). Productos cruzados y rotaciones en espacios euclidianos de 2 y 3 dimensiones. Universidad de California, Berkeley (PDF).
• El producto vectorial, Mathcentre (Reino Unido), 2009