En geometría , los poliedros sesgados regulares son generalizaciones al conjunto de poliedros regulares que incluyen la posibilidad de caras no planas o figuras de vértices . Coxeter observó figuras de vértices sesgados que crearon nuevos poliedros regulares de 4 dimensiones, y mucho más tarde Branko Grünbaum observó caras sesgadas regulares. [1]
Los poliedros sesgados regulares infinitos que abarcan 3 espacios o más se denominan apeiroedros sesgados regulares .
Según Coxeter , en 1926 John Flinders Petrie generalizó el concepto de polígonos sesgados regulares (polígonos no planos) a poliedros sesgados regulares .
Coxeter ofreció un símbolo de Schläfli modificado { l , m | n } para estas figuras, donde { l , m } implica la figura del vértice , m l -gons alrededor de un vértice y n -agujeros angulares. Sus figuras de vértices son polígonos sesgados , que zigzaguean entre dos planos.
Los poliedros sesgados regulares, representados por { l , m | n } , sigue esta ecuación:
Un primer conjunto { l , m | n } , repite los cinco sólidos platónicos convexos y un sólido de Kepler-Poinsot no convexo :
Coxeter también enumeró un conjunto más grande de poliedros regulares finitos en su artículo "poliedros sesgados regulares en tres y cuatro dimensiones, y sus análogos topológicos".
Así como los poliedros sesgados infinitos representan superficies múltiples entre las celdas de los panales uniformes convexos , todas las formas finitas representan superficies múltiples dentro de las celdas de los 4 politopos uniformes .
Poliedros de la forma {2p, 2q | r} están relacionados con la simetría del grupo de Coxeter de [(p,r,q,r)], que se reduce a [r,p,r] lineal cuando q es 2. Coxeter da esta simetría como [[( p , r , q , r )] + ] que, según él, es isomorfo a su grupo abstracto (2 p ,2 q |2, r ). El panal relacionado tiene la simetría extendida [[( p , r , q , r )]]. [2]
{2p,4|r} está representado por las caras {2p} del 4 politopo uniforme bitruncado {r,p,r} , y {4,2p|r} está representado por las caras cuadradas del {r,p runcinado ,r}.
{4,4|n} produce un duoprisma n - n , y específicamente {4,4|4} encaja dentro de un teseracto {4}x{4} .

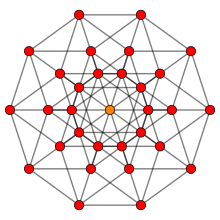
Un conjunto final se basa en la forma extendida de Coxeter {q1,m|q2,q3...} o con q2 sin especificar: {l, m |, q}. Estos también se pueden representar como un mapa finito regular o { l , m } 2 q , y el grupo G l , m , q . [3]
Los poliedros sesgados regulares también se pueden construir en dimensiones superiores a 4 como incrustaciones en politopos o panales regulares. Por ejemplo, el icosaedro regular puede estar incrustado en los vértices del 6-demicube ; HSM Coxeter lo denominó icosaedro sesgado regular . El dodecaedro se puede incrustar de manera similar en el demicubo de 10 . [4]