Oscilador armónico cuántico

Modelo mecánico cuántico importante y bien comprendido

Algunas trayectorias de un oscilador armónico según las leyes de Newton de la mecánica clásica (A–B), y según la ecuación de Schrödinger de la mecánica cuántica (C–H). En A–B, la partícula (representada como una bola unida a un resorte ) oscila de un lado a otro. En C–H, se muestran algunas soluciones a la ecuación de Schrödinger, donde el eje horizontal es la posición y el eje vertical es la parte real (azul) o imaginaria (roja) de la función de onda . C, D, E, F, pero no G, H, son estados propios de energía . H es un estado coherente , un estado cuántico que se aproxima a la trayectoria clásica.

El oscilador armónico cuántico es el análogo mecánico cuántico del oscilador armónico clásico . Debido a que un potencial suave arbitrario puede ser aproximado generalmente como un potencial armónico en la proximidad de un punto de equilibrio estable , es uno de los sistemas modelo más importantes en mecánica cuántica. Además, es uno de los pocos sistemas mecánicos cuánticos para los que se conoce una solución analítica exacta. ^{[1] [2] [3]}

Oscilador armónico unidimensional

Hamiltonianos y estados propios de energía

Representaciones de función de onda para los primeros ocho estados propios ligados, n = 0 a 7. El eje horizontal muestra la posición x .

Densidades de probabilidad correspondientes.

El hamiltoniano de la partícula es: donde m es la masa de la partícula, k es la constante de fuerza, es la frecuencia angular del oscilador, es el operador de posición (dado por x en la base de coordenadas), y es el operador de momento (dado por en la base de coordenadas). El primer término del hamiltoniano representa la energía cinética de la partícula, y el segundo término representa su energía potencial, como en la ley de Hooke . ^[4] $${\displaystyle {\hat {H}}={\frac {{\hat {p}}^{2}}{2m}}+{\frac {1}{2}}k{\hat {x}}^{2}={\frac {{\hat {p}}^{2}}{2m}}+{\frac {1}{2}}m\omega ^{2}{\hat {x}}^{2}\,,}$$ ${\textstyle \omega ={\sqrt {k/m}}}$ ${\displaystyle {\hat {x}}}$ ${\displaystyle {\hat {p}}}$ ${\displaystyle {\hat {p}}=-i\hbar \,\partial /\partial x}$

La ecuación de Schrödinger independiente del tiempo (TISE) es, donde denota un número real (que necesita ser determinado) que especificará un nivel de energía independiente del tiempo , o valor propio , y la solución denota el estado propio de energía de ese nivel . ^[5] $${\displaystyle {\hat {H}}\left|\psi \right\rangle =E\left|\psi \right\rangle ~,}$$ ${\displaystyle E}$ ${\displaystyle |\psi \rangle }$

Luego, resuelva la ecuación diferencial que representa este problema de valores propios en la base de coordenadas, para la función de onda , utilizando un método espectral . Resulta que existe una familia de soluciones. En esta base, ascienden a funciones de Hermite , ^{[6] [7]} ${\displaystyle \langle x|\psi \rangle =\psi (x)}$ $${\displaystyle \psi _{n}(x)={\frac {1}{\sqrt {2^{n}\,n!}}}\left({\frac {m\omega }{\pi \hbar }}\right)^{1/4}e^{-{\frac {m\omega x^{2}}{2\hbar }}}H_{n}\left({\sqrt {\frac {m\omega }{\hbar }}}x\right),\qquad n=0,1,2,\ldots .}$$

Las funciones H _n son los polinomios de Hermite de los físicos , $${\displaystyle H_{n}(z)=(-1)^{n}~e^{z^{2}}{\frac {d^{n}}{dz^{n}}}\left(e^{-z^{2}}\right).}$$

Los niveles de energía correspondientes son ^[8] Los valores esperados de posición y momento combinados con la varianza de cada variable se pueden derivar de la función de onda para comprender el comportamiento de los eigenkets de energía. Se muestra que son y debido a la simetría del problema, mientras que: $${\displaystyle E_{n}=\hbar \omega {\bigl (}n+{\tfrac {1}{2}}{\bigr )}.}$$ ${\textstyle \langle {\hat {x}}\rangle =0}$ ${\textstyle \langle {\hat {p}}\rangle =0}$

${\displaystyle \langle {\hat {x}}^{2}\rangle =(2n+1){\frac {\hbar }{2m\omega }}=\sigma _{x}^{2}}$

${\displaystyle \langle {\hat {p}}^{2}\rangle =(2n+1){\frac {m\hbar \omega }{2}}=\sigma _{p}^{2}}$

Se observa que la variación tanto en la posición como en el momento aumenta para los niveles de energía más altos. El nivel de energía más bajo tiene un valor que es su valor mínimo debido a la relación de incertidumbre y también corresponde a una función de onda gaussiana. ^[9] ${\textstyle \sigma _{x}\sigma _{p}={\frac {\hbar }{2}}}$

Este espectro de energía es notable por tres razones. Primero, las energías están cuantizadas, lo que significa que solo son posibles valores de energía discretos (múltiplos enteros más la mitad de ħω ); esta es una característica general de los sistemas mecánicos cuánticos cuando una partícula está confinada. Segundo, estos niveles de energía discretos están espaciados de manera uniforme, a diferencia del modelo de Bohr del átomo o la partícula en una caja . Tercero, la energía más baja alcanzable (la energía del estado n = 0 , llamado estado fundamental ) no es igual al mínimo del pozo de potencial, sino ħω /2 por encima de él; esto se llama energía de punto cero . Debido a la energía de punto cero, la posición y el momento del oscilador en el estado fundamental no son fijos (como lo serían en un oscilador clásico), sino que tienen un pequeño rango de varianza, de acuerdo con el principio de incertidumbre de Heisenberg .

La densidad de probabilidad del estado fundamental se concentra en el origen, lo que significa que la partícula pasa la mayor parte de su tiempo en el fondo del pozo de potencial, como se esperaría de un estado con poca energía. A medida que aumenta la energía, la densidad de probabilidad alcanza su punto máximo en los "puntos de inflexión" clásicos, donde la energía del estado coincide con la energía potencial (véase la discusión a continuación de los estados altamente excitados). Esto es coherente con el oscilador armónico clásico, en el que la partícula pasa la mayor parte de su tiempo (y, por lo tanto, es más probable que se la encuentre) cerca de los puntos de inflexión, donde se mueve más lentamente. De este modo, se satisface el principio de correspondencia . Además, los paquetes de ondas no dispersivos especiales , con una incertidumbre mínima, llamados estados coherentes , oscilan de forma muy similar a los objetos clásicos, como se ilustra en la figura; no son estados propios del hamiltoniano.

Método del operador de escalera

Densidades de probabilidad | ψ _n ( x )| ² para los estados propios ligados, comenzando con el estado fundamental ( n = 0) en la parte inferior y aumentando en energía hacia la parte superior. El eje horizontal muestra la posición x , y los colores más brillantes representan densidades de probabilidad más altas.

El método del " operador de escalera ", desarrollado por Paul Dirac , permite la extracción de los valores propios de energía sin resolver directamente la ecuación diferencial. ^[10] Es generalizable a problemas más complicados, en particular en la teoría cuántica de campos . Siguiendo este enfoque, definimos los operadores a y su adjunto a ^† . Nótese que estos operadores clásicamente son exactamente los generadores de rotación normalizada en el espacio de fase de y , es decir , describen la evolución hacia adelante y hacia atrás en el tiempo de un oscilador armónico clásico. ^{[ aclaración necesaria ]} $${\displaystyle {\begin{aligned}a&={\sqrt {m\omega \over 2\hbar }}\left({\hat {x}}+{i \over m\omega }{\hat {p}}\right)\\a^{\dagger }&={\sqrt {m\omega \over 2\hbar }}\left({\hat {x}}-{i \over m\omega }{\hat {p}}\right)\end{aligned}}}$$ ${\displaystyle x}$ ${\displaystyle m{\frac {dx}{dt}}}$

Estos operadores conducen a la siguiente representación de y , ${\displaystyle {\hat {x}}}$ ${\displaystyle {\hat {p}}}$ $${\displaystyle {\begin{aligned}{\hat {x}}&={\sqrt {\frac {\hbar }{2m\omega }}}(a^{\dagger }+a)\\{\hat {p}}&=i{\sqrt {\frac {\hbar m\omega }{2}}}(a^{\dagger }-a)~.\end{aligned}}}$$

El operador a no es hermítico , ya que él mismo y su adjunto a ^† no son iguales. Los estados propios de energía | n ⟩ , cuando se operan con estos operadores de escalera, dan $${\displaystyle {\begin{aligned}a^{\dagger }|n\rangle &={\sqrt {n+1}}|n+1\rangle \\a|n\rangle &={\sqrt {n}}|n-1\rangle .\end{aligned}}}$$

A partir de las relaciones anteriores, también podemos definir un operador numérico N , que tiene la siguiente propiedad: $${\displaystyle {\begin{aligned}N&=a^{\dagger }a\\N\left|n\right\rangle &=n\left|n\right\rangle .\end{aligned}}}$$

Los siguientes conmutadores se pueden obtener fácilmente sustituyendo la relación de conmutación canónica , $${\displaystyle [a,a^{\dagger }]=1,\qquad [N,a^{\dagger }]=a^{\dagger },\qquad [N,a]=-a,}$$

y el operador de Hamilton se puede expresar como $${\displaystyle {\hat {H}}=\hbar \omega \left(N+{\frac {1}{2}}\right),}$$

Por lo tanto, los estados propios de N son también los estados propios de la energía. Para comprobarlo, podemos aplicar a un estado numérico : ${\displaystyle {\hat {H}}}$ ${\displaystyle |n\rangle }$

$${\displaystyle {\hat {H}}|n\rangle =\hbar \omega \left({\hat {N}}+{\frac {1}{2}}\right)|n\rangle .}$$

Usando la propiedad del operador numérico : ${\displaystyle {\hat {N}}}$

$${\displaystyle {\hat {N}}|n\rangle =n|n\rangle ,}$$

obtenemos:

$${\displaystyle {\hat {H}}|n\rangle =\hbar \omega \left(n+{\frac {1}{2}}\right)|n\rangle .}$$

Por lo tanto, dado que resuelve el TISE para el operador hamiltoniano , es también uno de sus estados propios con el valor propio correspondiente: ${\displaystyle |n\rangle }$ ${\displaystyle {\hat {H}}}$

$${\displaystyle E_{n}=\hbar \omega \left(n+{\frac {1}{2}}\right).}$$

QED.

La propiedad de conmutación produce $${\displaystyle {\begin{aligned}Na^{\dagger }|n\rangle &=\left(a^{\dagger }N+[N,a^{\dagger }]\right)|n\rangle \\&=\left(a^{\dagger }N+a^{\dagger }\right)|n\rangle \\&=(n+1)a^{\dagger }|n\rangle ,\end{aligned}}}$$

y de manera similar, $${\displaystyle Na|n\rangle =(n-1)a|n\rangle .}$$

Esto significa que a actúa sobre | n ⟩ para producir, hasta una constante multiplicativa, | n –1⟩ , y a ^† actúa sobre | n ⟩ para producir | n +1⟩ . Por esta razón, a se denomina operador de aniquilación ("operador de reducción"), y a ^† operador de creación ("operador de elevación"). Los dos operadores juntos se denominan operadores de escalera .

Dado cualquier estado propio de energía, podemos actuar sobre él con el operador de reducción, a , para producir otro estado propio con ħω menos energía. Mediante la aplicación repetida del operador de reducción, parece que podemos producir estados propios de energía hasta E = −∞ . Sin embargo, dado que $${\displaystyle n=\langle n|N|n\rangle =\langle n|a^{\dagger }a|n\rangle ={\Bigl (}a|n\rangle {\Bigr )}^{\dagger }a|n\rangle \geqslant 0,}$$

El valor propio más pequeño del operador numérico es 0, y $${\displaystyle a\left|0\right\rangle =0.}$$

En este caso, las aplicaciones posteriores del operador de reducción producirán simplemente cero, en lugar de estados propios de energía adicionales. Además, hemos demostrado anteriormente que $${\displaystyle {\hat {H}}\left|0\right\rangle ={\frac {\hbar \omega }{2}}\left|0\right\rangle }$$

Finalmente, actuando sobre |0⟩ con el operador de elevación y multiplicando por factores de normalización adecuados , podemos producir un conjunto infinito de estados propios de energía. $${\displaystyle \left\{\left|0\right\rangle ,\left|1\right\rangle ,\left|2\right\rangle ,\ldots ,\left|n\right\rangle ,\ldots \right\},}$$

de manera que coincida con el espectro de energía dado en la sección anterior. $${\displaystyle {\hat {H}}\left|n\right\rangle =\hbar \omega \left(n+{\frac {1}{2}}\right)\left|n\right\rangle ,}$$

Los estados propios arbitrarios se pueden expresar en términos de |0⟩, ^[11] $${\displaystyle |n\rangle ={\frac {(a^{\dagger })^{n}}{\sqrt {n!}}}|0\rangle .}$$

Prueba

$${\displaystyle {\begin{aligned}\langle n|aa^{\dagger }|n\rangle &=\langle n|\left([a,a^{\dagger }]+a^{\dagger }a\right)\left|n\right\rangle =\langle n|\left(N+1\right)|n\rangle =n+1\\[1ex]\Rightarrow a^{\dagger }|n\rangle &={\sqrt {n+1}}|n+1\rangle \\[1ex]\Rightarrow |n\rangle &={\frac {1}{\sqrt {n}}}a^{\dagger }\left|n-1\right\rangle ={\frac {1}{\sqrt {n(n-1)}}}\left(a^{\dagger }\right)^{2}\left|n-2\right\rangle =\cdots ={\frac {1}{\sqrt {n!}}}\left(a^{\dagger }\right)^{n}\left|0\right\rangle .\end{aligned}}}$$

Preguntas analíticas

El análisis precedente es algebraico, utilizando únicamente las relaciones de conmutación entre los operadores de elevación y descenso. Una vez que se completa el análisis algebraico, se deben abordar cuestiones analíticas. En primer lugar, se debe encontrar el estado fundamental, es decir, la solución de la ecuación . En la representación de posición, esta es la ecuación diferencial de primer orden cuya solución se encuentra fácilmente como la gaussiana ^{[nb 1]} Conceptualmente, es importante que solo haya una solución de esta ecuación; si hubiera, digamos, dos estados fundamentales linealmente independientes, obtendríamos dos cadenas independientes de vectores propios para el oscilador armónico. Una vez que se calcula el estado fundamental, se puede demostrar inductivamente que los estados excitados son polinomios de Hermite multiplicados por el estado fundamental gaussiano, utilizando la forma explícita del operador de elevación en la representación de posición. También se puede demostrar que, como se esperaba a partir de la unicidad del estado fundamental, los estados propios de energía de las funciones de Hermite construidos por el método de escalera forman un conjunto ortonormal completo de funciones. ^[12] ${\displaystyle a\psi _{0}=0}$ $${\displaystyle \left(x+{\frac {\hbar }{m\omega }}{\frac {d}{dx}}\right)\psi _{0}=0,}$$ $${\displaystyle \psi _{0}(x)=Ce^{-{\frac {m\omega x^{2}}{2\hbar }}}.}$$ ${\displaystyle \psi _{n}}$

Conectando explícitamente con la sección anterior, el estado fundamental |0⟩ en la representación de la posición está determinado por , por lo tanto , de modo que , y así sucesivamente. ${\displaystyle a|0\rangle =0}$ $${\displaystyle \left\langle x\mid a\mid 0\right\rangle =0\qquad \Rightarrow \left(x+{\frac {\hbar }{m\omega }}{\frac {d}{dx}}\right)\left\langle x\mid 0\right\rangle =0\qquad \Rightarrow }$$ $${\displaystyle \left\langle x\mid 0\right\rangle =\left({\frac {m\omega }{\pi \hbar }}\right)^{\frac {1}{4}}\exp \left(-{\frac {m\omega }{2\hbar }}x^{2}\right)=\psi _{0}~,}$$ $${\displaystyle \langle x\mid a^{\dagger }\mid 0\rangle =\psi _{1}(x)~,}$$ ${\displaystyle \psi _{1}(x,t)=\langle x\mid e^{-3i\omega t/2}a^{\dagger }\mid 0\rangle }$

Escalas naturales de longitud y energía

El oscilador armónico cuántico posee escalas naturales de longitud y energía que pueden utilizarse para simplificar el problema. Estas pueden encontrarse mediante la adimensionalización .

El resultado es que, si la energía se mide en unidades de ħω y la distancia en unidades de √ ħ /( mω ) , entonces el hamiltoniano se simplifica a mientras que las funciones propias de energía y los valores propios se simplifican a funciones de Hermite y números enteros desplazados por un medio, donde H _n ( x ) son los polinomios de Hermite . $${\displaystyle H=-{\frac {1}{2}}{d^{2} \over dx^{2}}+{\frac {1}{2}}x^{2},}$$ $${\displaystyle \psi _{n}(x)=\left\langle x\mid n\right\rangle ={1 \over {\sqrt {2^{n}n!}}}~\pi ^{-1/4}\exp(-x^{2}/2)~H_{n}(x),}$$ $${\displaystyle E_{n}=n+{\tfrac {1}{2}}~,}$$

Para evitar confusiones, en este artículo no se adoptarán en su mayoría estas "unidades naturales". Sin embargo, suelen resultar útiles al realizar cálculos, ya que evitan el desorden.

Por ejemplo, la solución fundamental ( propagador ) de H − i∂ _t , el operador de Schrödinger dependiente del tiempo para este oscilador, simplemente se reduce al núcleo de Mehler , ^{[13] [14]} donde K ( x , y ;0) = δ ( x − y ) . La solución más general para una configuración inicial dada ψ ( x ,0) es entonces simplemente $${\displaystyle \langle x\mid \exp(-itH)\mid y\rangle \equiv K(x,y;t)={\frac {1}{\sqrt {2\pi i\sin t}}}\exp \left({\frac {i}{2\sin t}}\left((x^{2}+y^{2})\cos t-2xy\right)\right)~,}$$ $${\displaystyle \psi (x,t)=\int dy~K(x,y;t)\psi (y,0)\,.}$$

Estados coherentes

Evolución temporal de la distribución de probabilidad (y fase, mostrada en color) de un estado coherente con | α |=3.

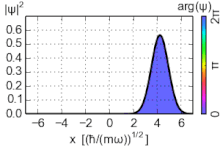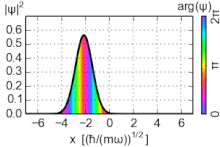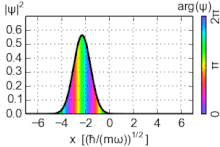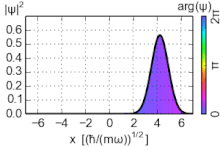
Los estados coherentes (también conocidos como estados de Glauber) del oscilador armónico son paquetes de ondas no dispersivos especiales , con una incertidumbre mínima σ _x σ _p = ℏ ⁄ 2 , cuyos valores esperados de observables evolucionan como un sistema clásico. Son vectores propios del operador de aniquilación, no del hamiltoniano, y forman una base sobrecompleta que, en consecuencia, carece de ortogonalidad. ^[15]

Los estados coherentes están indexados y expresados ​​en la base | n ⟩ como ${\displaystyle \alpha \in \mathbb {C} }$

$${\displaystyle |\alpha \rangle =\sum _{n=0}^{\infty }|n\rangle \langle n|\alpha \rangle =e^{-{\frac {1}{2}}|\alpha |^{2}}\sum _{n=0}^{\infty }{\frac {\alpha ^{n}}{\sqrt {n!}}}|n\rangle =e^{-{\frac {1}{2}}|\alpha |^{2}}e^{\alpha a^{\dagger }}e^{-{\alpha ^{*}a}}|0\rangle .}$$

Dado que los estados coherentes no son estados propios de energía, su evolución temporal no es un simple cambio de fase de la función de onda. Sin embargo, los estados evolucionados en el tiempo también son estados coherentes, pero con un parámetro de cambio de fase α : . ${\displaystyle \alpha (t)=\alpha (0)e^{-i\omega t}=\alpha _{0}e^{-i\omega t}}$ $${\displaystyle |\alpha (t)\rangle =\sum _{n=0}^{\infty }e^{-i\left(n+{\frac {1}{2}}\right)\omega t}|n\rangle \langle n|\alpha \rangle =e^{\frac {-i\omega t}{2}}e^{-{\frac {1}{2}}|\alpha |^{2}}\sum _{n=0}^{\infty }{\frac {(\alpha e^{-i\omega t})^{n}}{\sqrt {n!}}}|n\rangle =e^{-{\frac {i\omega t}{2}}}|\alpha e^{-i\omega t}\rangle }$$

Debido a que y a través de la identidad de Kermack-McCrae, la última forma es equivalente a un operador de desplazamiento unitario que actúa sobre el estado fundamental: . Cálculo de los valores esperados: ${\displaystyle a\left|0\right\rangle =0}$ ${\displaystyle |\alpha \rangle =e^{\alpha {\hat {a}}^{\dagger }-\alpha ^{*}{\hat {a}}}|0\rangle =D(\alpha )|0\rangle }$

${\displaystyle \langle {\hat {x}}\rangle _{\alpha (t)}={\sqrt {\frac {2\hbar }{m\omega }}}|\alpha _{0}|\cos {(\omega t-\phi )}}$

${\displaystyle \langle {\hat {p}}\rangle _{\alpha (t)}=-{\sqrt {2m\hbar \omega }}|\alpha _{0}|\sin {(\omega t-\phi )}}$

donde es la fase aportada por el complejo α . Estas ecuaciones confirman el comportamiento oscilatorio de la partícula. ${\displaystyle \phi }$

Las incertidumbres calculadas mediante el método numérico son:

${\displaystyle \sigma _{x}(t)={\sqrt {\frac {\hbar }{2m\omega }}}}$

${\displaystyle \sigma _{p}(t)={\sqrt {\frac {m\hbar \omega }{2}}}}$

lo que da . Dado que la única función de onda que puede tener la incertidumbre de posición-momento más baja, , es una función de onda gaussiana, y dado que la función de onda de estado coherente tiene una incertidumbre de posición-momento mínima, observamos que la función de onda gaussiana general en mecánica cuántica tiene la forma: Sustituyendo los valores esperados como una función del tiempo, da la función de onda variable en el tiempo requerida. ${\textstyle \sigma _{x}(t)\sigma _{p}(t)={\frac {\hbar }{2}}}$ ${\textstyle {\frac {\hbar }{2}}}$ $${\displaystyle \psi _{\alpha }(x')=\left({\frac {m\omega }{\pi \hbar }}\right)^{\frac {1}{4}}e^{{\frac {i}{\hbar }}\langle {\hat {p}}\rangle _{\alpha }(x'-{\frac {\langle {\hat {x}}\rangle _{\alpha }}{2}})-{\frac {m\omega }{2\hbar }}(x'-\langle {\hat {x}}\rangle _{\alpha })^{2}}.}$$

La probabilidad de cada estado propio de energía se puede calcular para encontrar la distribución de energía de la función de onda:

${\displaystyle P(E_{n})=|\langle n|\alpha \rangle |^{2}={\frac {e^{-|\alpha |^{2}}|\alpha |^{2n}}{n!}}}$

que corresponde a la distribución de Poisson .

Estados de alta excitación

Función de onda (arriba) y densidad de probabilidad (abajo) para el estado excitado n = 30 del oscilador armónico cuántico. Las líneas discontinuas verticales indican los puntos de inflexión clásicos, mientras que la línea de puntos representa la densidad de probabilidad clásica.

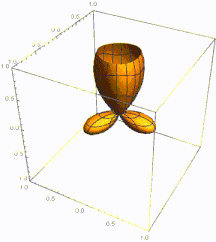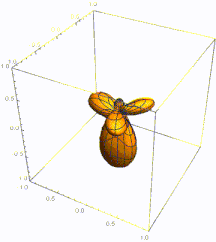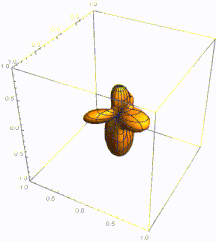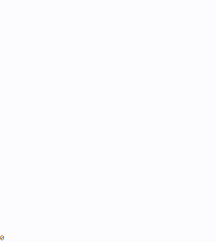
Cuando n es grande, los estados propios se localizan en la región clásica permitida, es decir, la región en la que una partícula clásica con energía E _n puede moverse. Los estados propios alcanzan su máximo cerca de los puntos de inflexión: los puntos en los extremos de la región clásicamente permitida donde la partícula clásica cambia de dirección. Este fenómeno se puede verificar a través de la asintótica de los polinomios de Hermite y también a través de la aproximación WKB .

La frecuencia de oscilación en x es proporcional al momento p ( x ) de una partícula clásica de energía E _n y posición x . Además, el cuadrado de la amplitud (que determina la densidad de probabilidad) es inversamente proporcional a p ( x ) , lo que refleja el tiempo que la partícula clásica pasa cerca de x . El comportamiento del sistema en una pequeña vecindad del punto de inflexión no tiene una explicación clásica simple, pero se puede modelar utilizando una función de Airy . Utilizando las propiedades de la función de Airy, se puede estimar que la probabilidad de encontrar la partícula fuera de la región clásicamente permitida es aproximadamente Esto también se da, asintóticamente, por la integral $${\displaystyle {\frac {2}{n^{1/3}3^{2/3}\Gamma ^{2}({\tfrac {1}{3}})}}={\frac {1}{n^{1/3}\cdot 7.46408092658...}}}$$ $${\displaystyle {\frac {1}{2\pi }}\int _{0}^{\infty }e^{(2n+1)\left(x-{\tfrac {1}{2}}\sinh(2x)\right)}dx~.}$$

Soluciones de espacio de fases

En la formulación del espacio de fases de la mecánica cuántica, los estados propios del oscilador armónico cuántico en varias representaciones diferentes de la distribución de cuasiprobabilidad se pueden escribir en forma cerrada. La más utilizada de ellas es la distribución de cuasiprobabilidad de Wigner .

La distribución de cuasiprobabilidad de Wigner para el estado propio de energía | n ⟩ es, en las unidades naturales descritas anteriormente, ^{[ cita requerida ]} donde L _n son los polinomios de Laguerre . Este ejemplo ilustra cómo los polinomios de Hermite y Laguerre están vinculados a través de la función de Wigner . $${\displaystyle F_{n}(x,p)={\frac {(-1)^{n}}{\pi \hbar }}L_{n}\left(2(x^{2}+p^{2})\right)e^{-(x^{2}+p^{2})}\,,}$$

Mientras tanto, la función Q de Husimi de los estados propios del oscilador armónico tiene una forma aún más simple. Si trabajamos en las unidades naturales descritas anteriormente, tenemos Esta afirmación se puede verificar utilizando la transformada de Segal-Bargmann . Específicamente, dado que el operador de elevación en la representación de Segal-Bargmann es simplemente la multiplicación por y el estado fundamental es la función constante 1, los estados del oscilador armónico normalizado en esta representación son simplemente . En este punto, podemos apelar a la fórmula para la función Q de Husimi en términos de la transformada de Segal-Bargmann. $${\displaystyle Q_{n}(x,p)={\frac {(x^{2}+p^{2})^{n}}{n!}}{\frac {e^{-(x^{2}+p^{2})}}{\pi }}}$$ ${\displaystyle z=x+ip}$ ${\displaystyle z^{n}/{\sqrt {n!}}}$

norte-oscilador armónico isotrópico dimensional

El oscilador armónico unidimensional se puede generalizar fácilmente a N dimensiones, donde N = 1, 2, 3, … . En una dimensión, la posición de la partícula se especificó mediante una única coordenada , x . En N dimensiones, esto se reemplaza por N coordenadas de posición, que etiquetamos x ₁ , …, x _N . A cada coordenada de posición corresponde un momento; los etiquetamos p ₁ , …, p _N . Las relaciones de conmutación canónicas entre estos operadores son $${\displaystyle {\begin{aligned}{[}x_{i},p_{j}{]}&=i\hbar \delta _{i,j}\\{[}x_{i},x_{j}{]}&=0\\{[}p_{i},p_{j}{]}&=0\end{aligned}}}$$

El hamiltoniano para este sistema es $${\displaystyle H=\sum _{i=1}^{N}\left({p_{i}^{2} \over 2m}+{1 \over 2}m\omega ^{2}x_{i}^{2}\right).}$$

Como lo deja claro la forma de este hamiltoniano, el oscilador armónico N -dimensional es exactamente análogo a N osciladores armónicos unidimensionales independientes con la misma masa y constante de resorte. En este caso, las cantidades x ₁ , ..., x _N se referirían a las posiciones de cada una de las N partículas. Esta es una propiedad conveniente del potencial r ² , que permite separar la energía potencial en términos que dependen de una coordenada cada uno.

Esta observación hace que la solución sea sencilla. Para un conjunto particular de números cuánticos, las funciones propias de energía para el oscilador N -dimensional se expresan en términos de las funciones propias unidimensionales como: ${\displaystyle \{n\}\equiv \{n_{1},n_{2},\dots ,n_{N}\}}$

$${\displaystyle \langle \mathbf {x} |\psi _{\{n\}}\rangle =\prod _{i=1}^{N}\langle x_{i}\mid \psi _{n_{i}}\rangle }$$

En el método del operador de escalera, definimos N conjuntos de operadores de escalera,

$${\displaystyle {\begin{aligned}a_{i}&={\sqrt {m\omega \over 2\hbar }}\left(x_{i}+{i \over m\omega }p_{i}\right),\\a_{i}^{\dagger }&={\sqrt {m\omega \over 2\hbar }}\left(x_{i}-{i \over m\omega }p_{i}\right).\end{aligned}}}$$

Mediante un procedimiento análogo al caso unidimensional, podemos demostrar que cada uno de los operadores a _i y a ^† _i disminuyen y aumentan la energía en ℏω respectivamente. El hamiltoniano es Este hamiltoniano es invariante bajo el grupo de simetría dinámica U ( N ) (el grupo unitario en N dimensiones), definido por donde es un elemento en la representación matricial definitoria de U ( N ) . $${\displaystyle H=\hbar \omega \,\sum _{i=1}^{N}\left(a_{i}^{\dagger }\,a_{i}+{\frac {1}{2}}\right).}$$ $${\displaystyle U\,a_{i}^{\dagger }\,U^{\dagger }=\sum _{j=1}^{N}a_{j}^{\dagger }\,U_{ji}\quad {\text{for all}}\quad U\in U(N),}$$ ${\displaystyle U_{ji}}$

Los niveles de energía del sistema son $${\displaystyle E=\hbar \omega \left[(n_{1}+\cdots +n_{N})+{N \over 2}\right].}$$ $${\displaystyle n_{i}=0,1,2,\dots \quad ({\text{the energy level in dimension }}i).}$$

Al igual que en el caso unidimensional, la energía está cuantizada. La energía del estado fundamental es N veces la energía fundamental unidimensional, como cabría esperar utilizando la analogía con N osciladores unidimensionales independientes. Hay una diferencia más: en el caso unidimensional, cada nivel de energía corresponde a un estado cuántico único. En N dimensiones, a excepción del estado fundamental, los niveles de energía están degenerados , lo que significa que hay varios estados con la misma energía.

La degeneración se puede calcular con relativa facilidad. Como ejemplo, considere el caso tridimensional: Defina n = n ₁ + n ₂ + n ₃ . Todos los estados con el mismo n tendrán la misma energía. Para un n dado , elegimos un n ₁ particular . Entonces n ₂ + n ₃ = n − n ₁ . Hay n − n ₁ + 1 pares posibles { n ₂ , n ₃ } . n ₂ puede tomar los valores de 0 a n − n ₁ , y para cada n ₂ el valor de n ₃ es fijo. Por lo tanto, el grado de degeneración es: Fórmula para N y n generales [ siendo g _n la dimensión de la representación de potencia n -ésima irreducible simétrica del grupo unitario U ( N ) ]: El caso especial N = 3, dado anteriormente, se sigue directamente de esta ecuación general. Sin embargo, esto solo es cierto para partículas distinguibles, o una partícula en N dimensiones (ya que las dimensiones son distinguibles). Para el caso de N bosones en una trampa armónica unidimensional, la degeneración se escala como el número de formas de particionar un entero n utilizando números enteros menores o iguales a N. $${\displaystyle g_{n}=\sum _{n_{1}=0}^{n}n-n_{1}+1={\frac {(n+1)(n+2)}{2}}}$$ $${\displaystyle g_{n}={\binom {N+n-1}{n}}}$$

$${\displaystyle g_{n}=p(N_{-},n)}$$

Esto surge debido a la restricción de poner N cuantos en un estado ket donde y , que son las mismas restricciones que en la partición de enteros. ${\textstyle \sum _{k=0}^{\infty }kn_{k}=n}$ ${\textstyle \sum _{k=0}^{\infty }n_{k}=N}$

Ejemplo: oscilador armónico isotrópico 3D

Soluciones orbitales armónicas esféricas 3D de Schrödinger en gráficos de densidad 2D; el código fuente de Mathematica que se utilizó para generar los gráficos se encuentra en la parte superior

La ecuación de Schrödinger para una partícula en un oscilador armónico tridimensional con simetría esférica se puede resolver explícitamente mediante la separación de variables. Este procedimiento es análogo a la separación realizada en el problema del átomo similar al hidrógeno , pero con un potencial con simetría esférica diferente, donde μ es la masa de la partícula. Como m se utilizará a continuación para el número cuántico magnético, la masa se indica mediante μ , en lugar de m , como se indicó anteriormente en este artículo. $${\displaystyle V(r)={1 \over 2}\mu \omega ^{2}r^{2},}$$

La solución de la ecuación es: ^[16] donde $${\displaystyle \psi _{klm}(r,\theta ,\phi )=N_{kl}r^{l}e^{-\nu r^{2}}L_{k}^{\left(l+{1 \over 2}\right)}(2\nu r^{2})Y_{lm}(\theta ,\phi )}$$

${\displaystyle N_{kl}={\sqrt {{\sqrt {\frac {2\nu ^{3}}{\pi }}}{\frac {2^{k+2l+3}\;k!\;\nu ^{l}}{(2k+2l+1)!!}}}}~~}$es una constante de normalización; ; ${\displaystyle \nu \equiv {\mu \omega \over 2\hbar }~}$

${\displaystyle {L_{k}}^{(l+{1 \over 2})}(2\nu r^{2})}$

son polinomios de Laguerre generalizados ; El orden k del polinomio es un entero no negativo;

• ${\displaystyle Y_{lm}(\theta ,\phi )\,}$es una función armónica esférica ;
• ħ es la constante de Planck reducida : ${\displaystyle \hbar \equiv {\frac {h}{2\pi }}~.}$

El valor propio de la energía es La energía generalmente se describe mediante un único número cuántico $${\displaystyle E=\hbar \omega \left(2k+l+{\frac {3}{2}}\right).}$$ $${\displaystyle n\equiv 2k+l\,.}$$

Como k es un entero no negativo, para cada n par tenemos ℓ = 0, 2, …, n − 2, n y para cada n impar tenemos ℓ = 1, 3, …, n − 2, n . El número cuántico magnético m es un entero que satisface − ℓ ≤ m ≤ ℓ , por lo que para cada n y ℓ hay 2 ℓ + 1 estados cuánticos  diferentes , etiquetados por m . Por lo tanto, la degeneración en el nivel n es donde la suma comienza desde 0 o 1, según si n es par o impar. Este resultado está de acuerdo con la fórmula de dimensión anterior, y equivale a la dimensionalidad de una representación simétrica de SU(3) , ^[17] el grupo de degeneración relevante. $${\displaystyle \sum _{l=\ldots ,n-2,n}(2l+1)={(n+1)(n+2) \over 2}\,,}$$

Aplicaciones

Red de osciladores armónicos: fonones

La notación de un oscilador armónico se puede extender a una red unidimensional de muchas partículas. Consideremos una cadena armónica mecanocuántica unidimensional de N átomos idénticos. Este es el modelo mecanocuántico más simple de una red, y veremos cómo surgen los fonones a partir de él. El formalismo que desarrollaremos para este modelo es fácilmente generalizable a dos y tres dimensiones.

Al igual que en la sección anterior, denotamos las posiciones de las masas por x ₁ , x ₂ , … , medidas desde sus posiciones de equilibrio (es decir, x _i = 0 si la partícula i está en su posición de equilibrio). En dos o más dimensiones, las x _i son cantidades vectoriales. El hamiltoniano para este sistema es

$${\displaystyle \mathbf {H} =\sum _{i=1}^{N}{p_{i}^{2} \over 2m}+{1 \over 2}m\omega ^{2}\sum _{\{ij\}(nn)}(x_{i}-x_{j})^{2}\,,}$$donde m es la masa (supuestamente uniforme) de cada átomo, y x _i y p _i son los operadores de posición y momento para el i ésimo átomo y la suma se realiza sobre los vecinos más cercanos (nn). Sin embargo, es habitual reescribir el hamiltoniano en términos de los modos normales del vector de onda en lugar de en términos de las coordenadas de la partícula para poder trabajar en el espacio de Fourier más conveniente .

Superposición de tres dipolos oscilantes: ilustra la propagación temporal de la función de onda común para diferentes n, l, m

Introducimos, entonces, un conjunto de N "coordenadas normales" Q _k , definidas como las transformadas de Fourier discretas de las x s, y N "momentos conjugados" Π definidos como las transformadas de Fourier de las p s, $${\displaystyle Q_{k}={1 \over {\sqrt {N}}}\sum _{l}e^{ikal}x_{l}}$$ $${\displaystyle \Pi _{k}={1 \over {\sqrt {N}}}\sum _{l}e^{-ikal}p_{l}\,.}$$

La cantidad k _n será el número de onda del fonón, es decir 2 π dividido por la longitud de onda . Toma valores cuantizados, porque el número de átomos es finito.

Esto conserva las relaciones de conmutación deseadas tanto en el espacio real como en el espacio vectorial de onda.

Otra ilustración de la propagación temporal de la función de onda común para tres átomos diferentes enfatiza el efecto del momento angular en el comportamiento de la distribución.

$${\displaystyle {\begin{aligned}\left[x_{l},p_{m}\right]&=i\hbar \delta _{l,m}\\\left[Q_{k},\Pi _{k'}\right]&={1 \over N}\sum _{l,m}e^{ikal}e^{-ik'am}[x_{l},p_{m}]\\&={i\hbar \over N}\sum _{m}e^{iam(k-k')}=i\hbar \delta _{k,k'}\\\left[Q_{k},Q_{k'}\right]&=\left[\Pi _{k},\Pi _{k'}\right]=0~.\end{aligned}}}$$

A partir del resultado general es fácil demostrar, mediante trigonometría elemental, que el término de energía potencial es donde $${\displaystyle {\begin{aligned}\sum _{l}x_{l}x_{l+m}&={1 \over N}\sum _{kk'}Q_{k}Q_{k'}\sum _{l}e^{ial\left(k+k'\right)}e^{iamk'}=\sum _{k}Q_{k}Q_{-k}e^{iamk}\\\sum _{l}{p_{l}}^{2}&=\sum _{k}\Pi _{k}\Pi _{-k}~,\end{aligned}}}$$ $${\displaystyle {1 \over 2}m\omega ^{2}\sum _{j}(x_{j}-x_{j+1})^{2}={1 \over 2}m\omega ^{2}\sum _{k}Q_{k}Q_{-k}(2-e^{ika}-e^{-ika})={1 \over 2}m\sum _{k}{\omega _{k}}^{2}Q_{k}Q_{-k}~,}$$ $${\displaystyle \omega _{k}={\sqrt {2\omega ^{2}(1-\cos(ka))}}~.}$$

El hamiltoniano puede escribirse en el espacio vectorial de onda como $${\displaystyle \mathbf {H} ={1 \over {2m}}\sum _{k}\left({\Pi _{k}\Pi _{-k}}+m^{2}\omega _{k}^{2}Q_{k}Q_{-k}\right)~.}$$

Obsérvese que los acoplamientos entre las variables de posición se han transformado; si los Q y los Π fueran hermíticos (lo cual no son), el hamiltoniano transformado describiría N osciladores armónicos desacoplados .

La forma de cuantificación depende de la elección de las condiciones de contorno; para simplificar, imponemos condiciones de contorno periódicas , definiendo el átomo ( N +1) -ésimo como equivalente al primer átomo. Físicamente, esto corresponde a unir la cadena en sus extremos. La cuantificación resultante es

$${\displaystyle k=k_{n}={2n\pi \over Na}\quad {\hbox{for}}\ n=0,\pm 1,\pm 2,\ldots ,\pm {N \over 2}.}$$

El límite superior de n proviene de la longitud de onda mínima, que es el doble del espaciado reticular a , como se explicó anteriormente.

Los valores propios del oscilador armónico o niveles de energía para el modo ω _k son $${\displaystyle E_{n}=\left({1 \over 2}+n\right)\hbar \omega _{k}\quad {\hbox{for}}\quad n=0,1,2,3,\ldots }$$

Si ignoramos la energía del punto cero , entonces los niveles están espaciados uniformemente en $${\displaystyle {\tfrac {3}{2}}\hbar \omega ,\ {\tfrac {5}{2}}\hbar \omega ,\ {\tfrac {7}{2}}\hbar \omega \ \cdots }$$

Por lo tanto, se debe suministrar una cantidad exacta de energía ħω a la red del oscilador armónico para impulsarlo al siguiente nivel de energía. En analogía con el caso del fotón , cuando el campo electromagnético está cuantizado, el cuanto de energía vibracional se denomina fonón .

Todos los sistemas cuánticos presentan propiedades ondulatorias y corpusculares. Las propiedades corpusculares del fonón se entienden mejor utilizando los métodos de segunda cuantificación y las técnicas de operadores descritas en otros trabajos. ^[18]

En el límite continuo , a  → 0 , N  → ∞ , mientras que Na se mantiene fijo. Las coordenadas canónicas Q _k se transforman en los modos de momento desacoplados de un campo escalar, , mientras que el índice de ubicación i ( no la variable dinámica de desplazamiento ) se convierte en el argumento del parámetro x del campo escalar, . ${\displaystyle \phi _{k}}$ ${\displaystyle \phi (x,t)}$

Vibraciones moleculares

• Las vibraciones de una molécula diatómica son un ejemplo de una versión de dos cuerpos del oscilador armónico cuántico. En este caso, la frecuencia angular está dada por donde es la masa reducida y y son las masas de los dos átomos. ^[19] $${\displaystyle \omega ={\sqrt {\frac {k}{\mu }}}}$$ ${\displaystyle \mu ={\frac {m_{1}m_{2}}{m_{1}+m_{2}}}}$ ${\displaystyle m_{1}}$ ${\displaystyle m_{2}}$
• El átomo de Hooke es un modelo simple del átomo de helio que utiliza el oscilador armónico cuántico.
• Modelado de fonones, como se discutió anteriormente.
• Una carga con masa en un campo magnético uniforme es un ejemplo de un oscilador armónico cuántico unidimensional: cuantificación de Landau . ${\displaystyle q}$ ${\displaystyle m}$ ${\displaystyle \mathbf {B} }$

Véase también

• Péndulo cuántico
• Máquina cuántica  : dispositivo creado por el hombre cuyo movimiento colectivo sigue las leyes de la mecánica cuántica.Pages displaying wikidata descriptions as a fallback
• Gas en una trampa armónica  – Modelo mecánico cuántico
• Operadores de creación y aniquilación  : operadores útiles en mecánica cuántica
• Estado coherente  – Estado cuántico específico de un oscilador armónico cuántico
• Potencial de Morse  : modelo de la energía potencial de una molécula diatómica
• Teorema de Bertrand  – Teorema de física
• Núcleo de Mehler
• Vibración molecular  : movimiento periódico de los átomos de una molécula.

Notas

1. La constante de normalización es y satisface la condición de normalización . ${\displaystyle C=\left({\frac {m\omega }{\pi \hbar }}\right)^{{1}/{4}}}$ ${\displaystyle \int _{-\infty }^{\infty }\psi _{0}(x)^{*}\psi _{0}(x)dx=1}$

Referencias

1. Griffiths 2004.
2. Liboff 2002.
3. Rashid, Muneer A. (2006). "Transition amplitude for time-dependent linear harmonic oscillator with Linear time-dependent Terms added to the Hamiltonian" (PDF) . MA Rashid – Centro de Física y Matemáticas Avanzadas . Centro Nacional de Física . Archivado desde el original ( PDF - Microsoft PowerPoint ) el 3 de marzo de 2016 . Consultado el 19 de octubre de 2010 .
4. Zwiebach (2022), págs. 233-234.
5. Zwiebach (2022), pág. 234.
6. Zwiebach (2022), pág. 241.
7. Gbur, Gregory J. (2011). Métodos matemáticos para la física óptica y la ingeniería . Cambridge University Press. pp. 631–633. ISBN 978-0-521-51610-5.
8. Zwiebach (2022), pág. 240.
9. Zwiebach (2022), págs. 249-250.
10. Zwiebach (2022), págs. 246-249.
11. Zwiebach (2022), pág. 248.
12. Hall, Brian C. (2013), Teoría cuántica para matemáticos , Textos de posgrado en matemáticas, vol. 267, Springer, Teorema 11.4, Bibcode :2013qtm..book.....H, ISBN 978-1461471158
13. Pauli, W. (2000), Mecánica ondulatoria: Volumen 5 de Pauli Lectures on Physics (Dover Books on Physics). ISBN 978-0486414621  ; Sección 44. 
14. Condon, EU (1937). "Inmersión de la transformada de Fourier en un grupo continuo de transformaciones funcionales", Proc. Natl. Acad. Sci. USA 23 , 158–164. en línea
15. Zwiebach (2022), págs. 481–492.
16. Albert Messiah , Mecánica cuántica , 1967, Holanda Septentrional, cap. XII, § 15, pág. 456.en línea
17. Fradkin, DM (1965). "Oscilador armónico isotrópico tridimensional y SU3". American Journal of Physics . 33 (3): 207–211. doi :10.1119/1.1971373.
18. Mahan, GD (1981). Muchas partículas en física . Nueva York: Springer. ISBN 978-0306463389.
19. "Oscilador armónico cuántico". Hyperphysics . Consultado el 24 de septiembre de 2009 .

Bibliografía

• Griffiths, David J. (2004). Introducción a la mecánica cuántica (2.ª ed.). Prentice Hall. ISBN 978-0-13-805326-0.
• Liboff, Richard L. (2002). Introducción a la mecánica cuántica . Addison–Wesley. ISBN 978-0-8053-8714-8.
• Zwiebach, Barton (2022). Dominar la mecánica cuántica: conceptos básicos, teoría y aplicaciones . Prensa del MIT. ISBN 978-0-262-04613-8.

Enlaces externos

• Oscilador armónico cuántico
• Justificación para la elección de los operadores de escalera
• Gráficos de intensidad en 3D en vivo del oscilador armónico cuántico Archivado el 12 de julio de 2011 en Wayback Machine
• Oscilador armónico cuántico controlado y amortiguado (apuntes del curso "Óptica cuántica en circuitos eléctricos")