En matemáticas , la monodromía es el estudio de cómo se comportan los objetos del análisis matemático , la topología algebraica , la geometría algebraica y la geometría diferencial cuando "recorren" una singularidad . Como su nombre lo indica, el significado fundamental de la monodromía proviene de "recorrer en forma individual". Está estrechamente asociada con los mapas de recubrimiento y su degeneración en ramificaciones ; el aspecto que da lugar a los fenómenos de monodromía es que ciertas funciones que podríamos desear definir no son de valor único cuando "recorremos" un camino que rodea una singularidad. La falla de la monodromía se puede medir definiendo un grupo de monodromía : un grupo de transformaciones que actúan sobre los datos que codifican lo que sucede cuando "recorremos" en una dimensión. La falta de monodromía a veces se denomina polidromía . [1]
Sea X un espacio topológico de base conexo y localmente conexo con punto base x , y sea una cubierta con fibra . Para un bucle γ: [0, 1] → X con base en x , denotamos una elevación bajo la función de cubierta, que comienza en un punto , por . Finalmente, denotamos por el punto final , que generalmente es diferente de . Hay teoremas que establecen que esta construcción da una acción de grupo bien definida del grupo fundamental π 1 ( X , x ) sobre F , y que el estabilizador de es exactamente , es decir, un elemento [γ] fija un punto en F si y solo si está representado por la imagen de un bucle en con base en . Esta acción se llama acción de monodromía y el homomorfismo correspondiente π 1 ( X , x ) → Aut( H * ( F x )) en el grupo de automorfismos sobre F es la monodromía algebraica . La imagen de este homomorfismo es el grupo de monodromía . Existe otra función π 1 ( X , x ) → Diff( F x )/Is( F x ) cuya imagen se denomina grupo de monodromía topológica .
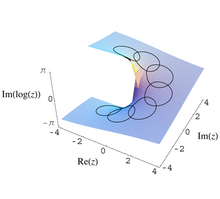
Estas ideas se hicieron explícitas por primera vez en el análisis complejo . En el proceso de continuación analítica , una función que es una función analítica F ( z ) en algún subconjunto abierto E del plano complejo perforado puede continuarse nuevamente en E , pero con valores diferentes. Por ejemplo, tomemos
Luego, continúa analíticamente en sentido antihorario alrededor del círculo.
dará como resultado el retorno, no a F ( z ) sino
En este caso, el grupo de monodromía es cíclico infinito y el espacio de recubrimiento es la cobertura universal del plano complejo perforado. Esta cobertura se puede visualizar como el helicoide (tal como se define en el artículo sobre el helicoide) restringido a ρ > 0 . El mapa de recubrimiento es una proyección vertical, en cierto sentido colapsa la espiral de la manera obvia para obtener un plano perforado.
Una aplicación importante es en ecuaciones diferenciales , donde una única solución puede dar otras soluciones linealmente independientes por continuación analítica . Las ecuaciones diferenciales lineales definidas en un conjunto abierto y conexo S en el plano complejo tienen un grupo de monodromía, que (más precisamente) es una representación lineal del grupo fundamental de S , que resume todas las continuaciones analíticas alrededor de los bucles dentro de S. El problema inverso, de construir la ecuación (con singularidades regulares ), dada una representación, es un problema de Riemann-Hilbert .
Para un sistema lineal regular (y en particular fuchsiano) se eligen habitualmente como generadores del grupo de monodromía los operadores M j correspondientes a bucles cada uno de los cuales rodea sólo uno de los polos del sistema en sentido antihorario. Si los índices j se eligen de tal forma que aumenten de 1 a p + 1 cuando se rodea el punto base en sentido horario, entonces la única relación entre los generadores es la igualdad . El problema de Deligne-Simpson es el siguiente problema de realización: ¿Para qué tuplas de clases de conjugación en GL( n , C ) existen tuplas irreducibles de matrices M j de estas clases que satisfacen la relación anterior? El problema ha sido formulado por Pierre Deligne y Carlos Simpson fue el primero en obtener resultados para su resolución. Una versión aditiva del problema sobre los residuos de los sistemas fuchsianos ha sido formulada y explorada por Vladimir Kostov. El problema ha sido considerado por otros autores también para grupos de matrices distintos de GL( n , C ). [2]
En el caso de un mapa de recubrimiento, lo vemos como un caso especial de una fibración , y usamos la propiedad de elevación de homotopía para "seguir" caminos en el espacio base X (asumimos que está conexo por caminos para simplificar) a medida que se elevan hacia la cubierta C. Si seguimos un bucle basado en x en X , que elevamos para comenzar en c por encima de x , terminaremos en algún c* nuevamente por encima de x ; es muy posible que c ≠ c* , y para codificar esto se considera la acción del grupo fundamental π 1 ( X , x ) como un grupo de permutación en el conjunto de todos los c , como un grupo de monodromía en este contexto.
En geometría diferencial, el transporte paralelo desempeña un papel análogo . En un fibrado principal B sobre una variedad lisa M , una conexión permite un movimiento "horizontal" desde fibras por encima de m en M hasta fibras adyacentes. El efecto, cuando se aplica a bucles basados en m, es definir un grupo holonomico de traslaciones de la fibra en m ; si el grupo de estructura de B es G , es un subgrupo de G que mide la desviación de B respecto del fibrado de productos M × G.
De manera análoga al grupoide fundamental, es posible prescindir de la elección de un punto base y definir un grupoide monodromía. Aquí consideramos (clases de homotopía de) elevaciones de caminos en el espacio base X de una fibración . El resultado tiene la estructura de un grupoide sobre el espacio base X. La ventaja es que podemos prescindir de la condición de conectividad de X.
Además, la construcción también se puede generalizar a foliaciones : considérese una foliación (posiblemente singular) de M . Entonces, para cada camino en una hoja de podemos considerar su difeomorfismo inducido en secciones transversales locales a través de los puntos finales. Dentro de un gráfico simplemente conexo, este difeomorfismo se vuelve único y especialmente canónico entre diferentes secciones transversales si pasamos al germen del difeomorfismo alrededor de los puntos finales. De esta manera, también se vuelve independiente del camino (entre puntos finales fijos) dentro de un gráfico simplemente conexo y, por lo tanto, es invariante bajo homotopía.
Sea F ( x ) el campo de las funciones racionales en la variable x sobre el campo F , que es el campo de fracciones del anillo polinomial F [ x ]. Un elemento y = f ( x ) de F ( x ) determina una extensión de campo finita [ F ( x ) : F ( y )].
Esta extensión generalmente no es Galois sino que tiene clausura de Galois L ( f ). El grupo de Galois asociado de la extensión [ L ( f ) : F ( y )] se llama grupo de monodromía de f .
En el caso de F = C entra en juego la teoría de superficies de Riemann y permite la interpretación geométrica dada anteriormente. En el caso de que la extensión [ C ( x ) : C ( y )] ya sea Galois, el grupo de monodromía asociado se denomina a veces grupo de transformaciones de barajas .
Esto tiene conexiones con la teoría de Galois de cubrir espacios que conduce al teorema de existencia de Riemann.