En química , la teoría de orbitales moleculares (teoría MO o MOT) es un método para describir la estructura electrónica de las moléculas utilizando la mecánica cuántica . Fue propuesta a principios del siglo XX. La MOT explica la naturaleza paramagnética del O 2 , que la teoría VSEPR no puede explicar.
En la teoría de orbitales moleculares, los electrones en una molécula no se asignan a enlaces químicos individuales entre átomos , sino que se consideran como si se movieran bajo la influencia de los núcleos atómicos en toda la molécula. [1] La mecánica cuántica describe las propiedades espaciales y energéticas de los electrones como orbitales moleculares que rodean a dos o más átomos en una molécula y contienen electrones de valencia entre los átomos.
La teoría de orbitales moleculares revolucionó el estudio de los enlaces químicos al aproximar los estados de los electrones enlazados (los orbitales moleculares) como combinaciones lineales de orbitales atómicos (LCAO). Estas aproximaciones se realizan aplicando la teoría del funcional de la densidad (DFT) o los modelos Hartree-Fock (HF) a la ecuación de Schrödinger .
La teoría de los orbitales moleculares y la teoría del enlace de valencia son las teorías fundamentales de la química cuántica .
En el método LCAO , cada molécula tiene un conjunto de orbitales moleculares . Se supone que la función de onda de los orbitales moleculares ψ j se puede escribir como una simple suma ponderada de los n orbitales atómicos constituyentes χ i , de acuerdo con la siguiente ecuación: [2]
Se pueden determinar numéricamente los coeficientes c ij sustituyendo esta ecuación en la ecuación de Schrödinger y aplicando el principio variacional . El principio variacional es una técnica matemática utilizada en mecánica cuántica para construir los coeficientes de cada base orbital atómica. Un coeficiente mayor significa que la base orbital está compuesta en mayor medida por ese orbital atómico contribuyente en particular; por lo tanto, el orbital molecular se caracteriza mejor por ese tipo. Este método de cuantificación de la contribución orbital como una combinación lineal de orbitales atómicos se utiliza en química computacional . Se puede aplicar una transformación unitaria adicional en el sistema para acelerar la convergencia en algunos esquemas computacionales. La teoría de orbitales moleculares se consideró un competidor de la teoría del enlace de valencia en la década de 1930, antes de que se comprendiera que los dos métodos están estrechamente relacionados y que, cuando se extienden, se vuelven equivalentes.
La teoría de orbitales moleculares se utiliza para interpretar la espectroscopia ultravioleta-visible (UV-VIS). Los cambios en la estructura electrónica de las moléculas se pueden ver por la absorción de luz en longitudes de onda específicas. Se pueden hacer asignaciones a estas señales indicadas por la transición de electrones que se mueven de un orbital de menor energía a un orbital de mayor energía. El diagrama de orbitales moleculares para el estado final describe la naturaleza electrónica de la molécula en un estado excitado.
Hay tres requisitos principales para que las combinaciones de orbitales atómicos sean adecuadas como orbitales moleculares aproximados.
La teoría de orbitales moleculares se desarrolló en los años posteriores al establecimiento de la teoría del enlace de valencia (1927), principalmente a través de los esfuerzos de Friedrich Hund , Robert Mulliken , John C. Slater y John Lennard-Jones . [4] La teoría de orbitales moleculares se llamó originalmente teoría de Hund-Mulliken. [5] Según el físico y químico físico Erich Hückel , el primer uso cuantitativo de la teoría de orbitales moleculares fue el artículo de 1929 de Lennard-Jones . [6] [7] Este artículo predijo un estado fundamental triplete para la molécula de dioxígeno que explicaba su paramagnetismo [8] (ver Diagrama de orbitales moleculares § Dioxígeno ) antes de la teoría del enlace de valencia, que presentó su propia explicación en 1931. [9] La palabra orbital fue introducida por Mulliken en 1932. [5] Para 1933, la teoría de orbitales moleculares había sido aceptada como una teoría válida y útil. [10]
Erich Hückel aplicó la teoría de orbitales moleculares a moléculas de hidrocarburos insaturados a partir de 1931 con su método de orbital molecular de Hückel (HMO) para la determinación de energías de MO para electrones pi , que aplicó a hidrocarburos conjugados y aromáticos. [11] [12] Este método proporcionó una explicación de la estabilidad de moléculas con seis electrones pi como el benceno .
El primer cálculo preciso de una función de onda de orbital molecular fue el realizado por Charles Coulson en 1938 sobre la molécula de hidrógeno. [13] En 1950, los orbitales moleculares se definieron completamente como funciones propias (funciones de onda) del hamiltoniano de campo autoconsistente y fue en este punto que la teoría de orbitales moleculares se volvió completamente rigurosa y consistente. [14] Este enfoque riguroso se conoce como el método Hartree-Fock para moléculas, aunque tuvo sus orígenes en cálculos sobre átomos. En los cálculos sobre moléculas, los orbitales moleculares se expanden en términos de un conjunto de bases orbitales atómicas , lo que conduce a las ecuaciones de Roothaan . [15] Esto condujo al desarrollo de muchos métodos de química cuántica ab initio . En paralelo, la teoría de orbitales moleculares se aplicó de una manera más aproximada utilizando algunos parámetros derivados empíricamente en métodos ahora conocidos como métodos de química cuántica semiempíricos . [15]
El éxito de la teoría de orbitales moleculares también generó la teoría del campo de ligandos , que se desarrolló durante las décadas de 1930 y 1940 como una alternativa a la teoría del campo cristalino .
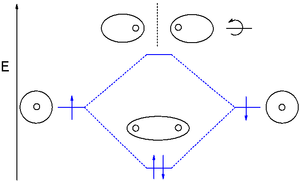
La teoría de orbitales moleculares (OM) utiliza una combinación lineal de orbitales atómicos (LCAO) para representar los orbitales moleculares resultantes de los enlaces entre átomos. Estos a menudo se dividen en tres tipos: enlazantes , antienlazantes y no enlazantes . Un orbital enlazante concentra la densidad electrónica en la región entre un par dado de átomos, de modo que su densidad electrónica tenderá a atraer cada uno de los dos núcleos hacia el otro y mantendrá unidos a los dos átomos. [16] Un orbital antienlazante concentra la densidad electrónica "detrás" de cada núcleo (es decir, en el lado de cada átomo que está más alejado del otro átomo), y por lo tanto tiende a alejar cada uno de los dos núcleos del otro y, en realidad, debilita el enlace entre los dos núcleos. Los electrones en orbitales no enlazantes tienden a estar asociados con orbitales atómicos que no interactúan positiva o negativamente entre sí, y los electrones en estos orbitales no contribuyen ni restan valor a la fuerza del enlace. [16]
Los orbitales moleculares se dividen a su vez según los tipos de orbitales atómicos a partir de los cuales se forman. Las sustancias químicas formarán interacciones de enlace si sus orbitales pierden energía al interactuar entre sí. Se distinguen diferentes orbitales de enlace que difieren por la configuración electrónica (forma de la nube de electrones) y por los niveles de energía .
Los orbitales moleculares de una molécula se pueden ilustrar en diagramas de orbitales moleculares .
Los orbitales de enlace más comunes son los orbitales sigma (σ), que son simétricos respecto del eje de enlace, y los orbitales pi (π), que tienen un plano nodal a lo largo del eje de enlace. Menos comunes son los orbitales delta (δ) y los orbitales phi (φ), que tienen dos y tres planos nodales, respectivamente, a lo largo del eje de enlace. Los orbitales antienlazantes se indican con un asterisco. Por ejemplo, un orbital antienlazante pi puede representarse como π*.

El orden de enlace es el número de enlaces químicos entre un par de átomos. El orden de enlace de una molécula se puede calcular restando el número de electrones en orbitales antienlazantes del número de orbitales enlazantes , y el número resultante se divide por dos. Se espera que una molécula sea estable si tiene un orden de enlace mayor que cero. Es adecuado considerar el electrón de valencia para determinar el orden de enlace. Porque (para el número cuántico principal , n>1) cuando los OM se derivan de AO 1s, la diferencia en el número de electrones en orbitales moleculares enlazantes y antienlazantes es cero. Por lo tanto, no hay un efecto neto en el orden de enlace si el electrón no es el de valencia.
Orden de enlace = 1/2 [(Número de electrones en el OM enlazante) - (Número de electrones en el OM antienlazante)]
A partir del orden de enlace, se puede predecir si se formará o no un enlace entre dos átomos. Por ejemplo, la existencia de la molécula de He 2 . A partir del diagrama de orbitales moleculares, el orden de enlace, = 1/2 * (2-2) = 0. Esto significa que no se formará ningún enlace entre dos átomos de He, lo que se observa experimentalmente. Se puede detectar con un haz molecular a muy baja temperatura y presión y tiene una energía de enlace de aproximadamente 0,001 J/mol. [17]
Además, la fuerza de un enlace también se puede calcular a partir del orden de enlace (BO). Por ejemplo:
H 2 :BO=(2-0)/2=1; Energía de enlace= 436 kJ/mol.
H 2 + :BO=(1-0)/2=1/2; Energía de enlace=171 kJ/mol.
Como el orden de enlace de H 2 + es menor que el de H 2 , debería ser menos estable, lo que se observa experimentalmente y se puede ver a partir de la energía de enlace.
La teoría de los enlaces químicos proporciona una perspectiva global y deslocalizada . En la teoría de los enlaces químicos, cualquier electrón de una molécula puede encontrarse en cualquier parte de la misma, ya que las condiciones cuánticas permiten que los electrones viajen bajo la influencia de un número arbitrario de núcleos, siempre que se encuentren en estados propios permitidos por ciertas reglas cuánticas. Por lo tanto, cuando se excitan con la cantidad necesaria de energía a través de luz de alta frecuencia u otros medios, los electrones pueden realizar la transición a orbitales moleculares de mayor energía. Por ejemplo, en el caso simple de una molécula diatómica de hidrógeno, la promoción de un solo electrón de un orbital de enlace a un orbital antienlazante puede ocurrir bajo la radiación UV. Esta promoción debilita el enlace entre los dos átomos de hidrógeno y puede conducir a la fotodisociación, la ruptura de un enlace químico debido a la absorción de luz.
La teoría de orbitales moleculares se utiliza para interpretar la espectroscopia ultravioleta-visible (UV-VIS). Los cambios en la estructura electrónica de las moléculas se pueden ver por la absorción de luz en longitudes de onda específicas. Se pueden hacer asignaciones a estas señales indicadas por la transición de electrones que se mueven de un orbital de menor energía a un orbital de mayor energía. El diagrama de orbitales moleculares para el estado final describe la naturaleza electrónica de la molécula en un estado excitado.
Aunque en la teoría de los orbitales moleculares algunos orbitales moleculares pueden albergar electrones que están más localizados entre pares específicos de átomos moleculares, otros orbitales pueden albergar electrones que están distribuidos de manera más uniforme sobre la molécula. Por lo tanto, en general, el enlace está mucho más deslocalizado en la teoría de los orbitales moleculares, lo que la hace más aplicable a moléculas resonantes que tienen órdenes de enlace no enteros equivalentes que la teoría del enlace de valencia . Esto hace que la teoría de los orbitales moleculares sea más útil para la descripción de sistemas extendidos.
Robert S. Mulliken , que participó activamente en el surgimiento de la teoría de los orbitales moleculares, considera que cada molécula es una unidad autosuficiente. En su artículo afirma:
... Los intentos de considerar que una molécula consiste en unidades atómicas o iónicas específicas unidas por un número discreto de electrones enlazantes o pares de electrones se consideran más o menos carentes de sentido, excepto como aproximación en casos especiales o como método de cálculo [...]. Una molécula se considera aquí como un conjunto de núcleos, alrededor de cada uno de los cuales se agrupa una configuración electrónica muy similar a la de un átomo libre en un campo externo, excepto que las partes externas de las configuraciones electrónicas que rodean cada núcleo pertenecen generalmente, en parte, conjuntamente a dos o más núcleos... [18]
Un ejemplo es la descripción MO del benceno , C
6yo
6, que es un anillo hexagonal aromático de seis átomos de carbono y tres enlaces dobles. En esta molécula, 24 de los 30 electrones de enlace de valencia totales (24 provenientes de átomos de carbono y 6 provenientes de átomos de hidrógeno) se encuentran en 12 orbitales de enlace σ (sigma), que se encuentran principalmente entre pares de átomos (CC o CH), de manera similar a los electrones en la descripción del enlace de valencia. Sin embargo, en el benceno, los seis electrones de enlace restantes se encuentran en tres orbitales de enlace molecular π (pi) que están deslocalizados alrededor del anillo. Dos de estos electrones están en un OM que tiene contribuciones orbitales iguales de los seis átomos. Los otros cuatro electrones están en orbitales con nodos verticales en ángulos rectos entre sí. Como en la teoría VB, todos estos seis electrones π deslocalizados residen en un espacio más grande que existe por encima y por debajo del plano del anillo. Todos los enlaces carbono-carbono en el benceno son químicamente equivalentes. En la teoría MO, esto es una consecuencia directa del hecho de que los tres orbitales moleculares π se combinan y distribuyen uniformemente los seis electrones adicionales entre seis átomos de carbono.
En moléculas como el metano , CH
4, los ocho electrones de valencia se encuentran en cuatro OM que se distribuyen en los cinco átomos. Es posible transformar los OM en cuatro orbitales sp 3 localizados . Linus Pauling, en 1931, hibridó los orbitales carbono 2s y 2p de modo que apuntaran directamente a las funciones base 1s del hidrógeno y presentaran una superposición máxima. Sin embargo, la descripción de OM deslocalizado es más apropiada para predecir las energías de ionización y las posiciones de las bandas de absorción espectral . Cuando se ioniza el metano, se toma un solo electrón de los OM de valencia, que puede provenir del enlace s o de los niveles de enlace p triplemente degenerado, lo que produce dos energías de ionización. En comparación, la explicación en la teoría del enlace de valencia es más complicada. Cuando se elimina un electrón de un orbital sp 3 , se invoca resonancia entre cuatro estructuras de enlace de valencia, cada una de las cuales tiene un solo enlace de un electrón y tres enlaces de dos electrones. Los estados ionizados triplemente degenerados T 2 y A 1 (CH 4 + ) se producen a partir de diferentes combinaciones lineales de estas cuatro estructuras. La diferencia de energía entre el estado ionizado y el fundamental da las dos energías de ionización.
Al igual que en el benceno, en sustancias como el betacaroteno , la clorofila o el hemo , algunos electrones en los orbitales π se distribuyen en orbitales moleculares a grandes distancias en una molécula, lo que resulta en la absorción de luz en energías más bajas (el espectro visible ), lo que explica los colores característicos de estas sustancias. [19] Estos y otros datos espectroscópicos para moléculas están bien explicados en la teoría de OM, con énfasis en los estados electrónicos asociados con orbitales multicéntricos, incluida la mezcla de orbitales basada en principios de coincidencia de simetría orbital. [16] Los mismos principios de OM también explican naturalmente algunos fenómenos eléctricos, como la alta conductividad eléctrica en la dirección plana de las láminas atómicas hexagonales que existen en el grafito . Esto resulta de la superposición de bandas continuas de orbitales p medio llenos y explica la conducción eléctrica. La teoría MO reconoce que algunos electrones en las láminas atómicas de grafito están completamente deslocalizados en distancias arbitrarias y residen en orbitales moleculares muy grandes que cubren toda una lámina de grafito, y algunos electrones son, por lo tanto, tan libres de moverse y, por lo tanto, conducen electricidad en el plano de la lámina, como si residieran en un metal.
{{cite book}}: CS1 maint: multiple names: authors list (link){{cite book}}: CS1 maint: multiple names: authors list (link)