Homocedasticidad y heterocedasticidad

Propiedad estadística

Gráfico con datos aleatorios que muestra homocedasticidad: en cada valor de x , el valor y de los puntos tiene aproximadamente la misma varianza .

Gráfico con datos aleatorios que muestra heterocedasticidad: la varianza de los valores y de los puntos aumenta con el aumento de los valores de x .

En estadística , una secuencia de variables aleatorias es homocedástica ( / ˌh oʊ m oʊ s k ə ˈ d æ s t ɪ k / ) si todas sus variables aleatorias tienen la misma varianza finita ; esto también se conoce como homogeneidad de varianza . La noción complementaria se llama heterocedasticidad , también conocida como heterogeneidad de varianza . Las grafías homos kedasticity y heteros kedasticity también se utilizan con frecuencia. “Scedasticidad” proviene de la palabra griega antigua “skedánnymi”, que significa “dispersar”. ^{[1] [2] [3]} Suponer que una variable es homocedástica cuando en realidad es heterocedástica ( / ˌ h ɛ t ər oʊ s k ə ˈ d æ s t ɪ k / ) da como resultado estimaciones puntuales imparciales pero ineficientes y estimaciones sesgadas de los errores estándar , y puede resultar en una sobreestimación de la bondad del ajuste medida por el coeficiente de Pearson .

La existencia de heterocedasticidad es una preocupación importante en el análisis de regresión y el análisis de varianza , ya que invalida las pruebas estadísticas de significancia que suponen que todos los errores de modelado tienen la misma varianza. Si bien el estimador de mínimos cuadrados ordinarios sigue siendo imparcial en presencia de heterocedasticidad, es ineficiente y la inferencia basada en el supuesto de homocedasticidad es engañosa. En ese caso, los mínimos cuadrados generalizados (GLS) se usaban con frecuencia en el pasado. ^{[4] [5]} Hoy en día, la práctica estándar en econometría es incluir errores estándar consistentes con la heterocedasticidad en lugar de usar GLS, ya que GLS puede exhibir un fuerte sesgo en muestras pequeñas si se desconoce la función cedástica real. ^[6]

Dado que la heterocedasticidad se refiere a las expectativas del segundo momento de los errores, su presencia se denomina especificación errónea de segundo orden. ^[7]

El econometrista Robert Engle recibió el Premio Nobel de Economía en 2003 por sus estudios sobre el análisis de regresión en presencia de heterocedasticidad, lo que condujo a su formulación de la técnica de modelado de heterocedasticidad condicional autorregresiva (ARCH). ^[8]

Definición

Considere la ecuación de regresión lineal donde la variable aleatoria dependiente es igual a la variable determinista multiplicada por el coeficiente más un término de perturbación aleatoria que tiene media cero. Las perturbaciones son homocedásticas si la varianza de es una constante ; de lo contrario, son heterocedásticas. En particular, las perturbaciones son heterocedásticas si la varianza de depende de o del valor de . Una forma en que podrían ser heterocedásticas es si (un ejemplo de una función cedástica ), por lo que la varianza es proporcional al valor de . ${\displaystyle y_{i}=x_{i}\beta _{i}+\varepsilon _{i},\ i=1,\ldots ,N,}$ ${\displaystyle y_{i}}$ ${\displaystyle x_{i}}$ ${\displaystyle \beta _{i}}$ ${\displaystyle \varepsilon _{i}}$ ${\displaystyle \varepsilon _{i}}$ ${\displaystyle \sigma ^{2}}$ ${\displaystyle \varepsilon _{i}}$ ${\displaystyle i}$ ${\displaystyle x_{i}}$ ${\displaystyle \sigma _{i}^{2}=x_{i}\sigma ^{2}}$ ${\displaystyle x}$

En términos más generales, si la matriz de varianza-covarianza de la perturbación a lo largo del tiempo tiene una diagonal no constante, la perturbación es heterocedástica. ^[9] Las matrices a continuación son covarianzas cuando hay solo tres observaciones a lo largo del tiempo. La perturbación en la matriz A es homocedástica; este es el caso simple donde MCO es el mejor estimador lineal insesgado. Las perturbaciones en las matrices B y C son heterocedásticas. En la matriz B, la varianza varía con el tiempo y aumenta de manera constante a lo largo del tiempo; en la matriz C, la varianza depende del valor de . La perturbación en la matriz D es homocedástica porque las varianzas diagonales son constantes, aunque las covarianzas fuera de la diagonal no son cero y los mínimos cuadrados ordinarios son ineficientes por una razón diferente: la correlación serial. ${\displaystyle \varepsilon _{i}}$ ${\displaystyle i}$ ${\displaystyle x}$

${\displaystyle {\begin{aligned}A&=\sigma ^{2}{\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\\\end{bmatrix}}&B&=\sigma ^{2}{\begin{bmatrix}1&0&0\\0&2&0\\0&0&3\\\end{bmatrix}}&C&=\sigma ^{2}{\begin{bmatrix}x_{1}&0&0\\0&x_{2}&0\\0&0&x_{3}\\\end{bmatrix}}&D&=\sigma ^{2}{\begin{bmatrix}1&\rho &\rho ^{2}\\\rho &1&\rho \\\rho ^{2}&\rho &1\\\end{bmatrix}}\end{aligned}}}$

Ejemplos

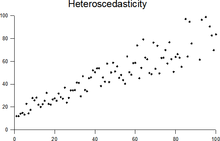
La heterocedasticidad a menudo ocurre cuando hay una gran diferencia entre los tamaños de las observaciones.

Un ejemplo clásico de heterocedasticidad es el de los ingresos frente a los gastos en alimentación. Una persona rica puede comer alimentos baratos a veces y alimentos caros en otras ocasiones. Una persona pobre casi siempre comerá alimentos baratos. Por lo tanto, las personas con mayores ingresos muestran una mayor variabilidad en los gastos en alimentación.

En el lanzamiento de un cohete, un observador mide la distancia recorrida por el cohete una vez por segundo. En los primeros segundos, las mediciones pueden tener una precisión de un centímetro. Después de cinco minutos, la precisión de las mediciones puede ser buena sólo hasta los 100 m, debido al aumento de la distancia, la distorsión atmosférica y una variedad de otros factores. Por lo tanto, las mediciones de distancia pueden presentar heterocedasticidad.

Consecuencias

Uno de los supuestos del modelo clásico de regresión lineal es que no hay heterocedasticidad. Romper este supuesto significa que el teorema de Gauss-Markov no se aplica, lo que significa que los estimadores MCO no son los mejores estimadores lineales insesgados (BLUE) y su varianza no es la más baja de todos los demás estimadores insesgados. La heterocedasticidad no hace que las estimaciones de los coeficientes de mínimos cuadrados ordinarios sean sesgadas, aunque puede hacer que las estimaciones de mínimos cuadrados ordinarios de la varianza (y, por lo tanto, los errores estándar) de los coeficientes sean sesgadas, posiblemente por encima o por debajo de la varianza real de la población. Por lo tanto, el análisis de regresión que utiliza datos heterocedásticos seguirá proporcionando una estimación insesgada de la relación entre la variable predictora y el resultado, pero los errores estándar y, por lo tanto, las inferencias obtenidas del análisis de datos son sospechosas. Los errores estándar sesgados conducen a una inferencia sesgada, por lo que los resultados de las pruebas de hipótesis posiblemente sean erróneos. Por ejemplo, si se realiza un MCO en un conjunto de datos heterocedásticos, lo que produce una estimación de error estándar sesgada, un investigador podría no rechazar una hipótesis nula en un nivel de significancia dado , cuando esa hipótesis nula en realidad no es característica de la población real (cometiendo un error de tipo II ).

Bajo ciertas suposiciones, el estimador MCO tiene una distribución asintótica normal cuando está correctamente normalizado y centrado (incluso cuando los datos no provienen de una distribución normal ). Este resultado se utiliza para justificar el uso de una distribución normal, o una distribución de chi cuadrado (dependiendo de cómo se calcule la estadística de prueba ), al realizar una prueba de hipótesis . Esto se mantiene incluso bajo heterocedasticidad. Más precisamente, el estimador MCO en presencia de heterocedasticidad es asintóticamente normal, cuando está correctamente normalizado y centrado, con una matriz de varianza-covarianza que difiere del caso de homocedasticidad. En 1980, White propuso un estimador consistente para la matriz de varianza-covarianza de la distribución asintótica del estimador MCO. ^[2] Esto valida el uso de pruebas de hipótesis utilizando estimadores MCO y el estimador de varianza-covarianza de White bajo heterocedasticidad.

La heterocedasticidad también es un problema práctico importante que se plantea en los problemas ANOVA . ^[10] La prueba F todavía se puede utilizar en algunas circunstancias. ^[11]

Sin embargo, se ha dicho que los estudiantes de econometría no deberían reaccionar exageradamente a la heterocedasticidad. ^[3] Un autor escribió: "la varianza de error desigual solo vale la pena corregirla cuando el problema es grave". ^[12] Además, otra advertencia estaba en la forma: "la heterocedasticidad nunca ha sido una razón para descartar un modelo que, por lo demás, es bueno". ^{[3] [13]} Con la llegada de los errores estándar consistentes con la heterocedasticidad que permiten la inferencia sin especificar el segundo momento condicional del término de error, probar la homocedasticidad condicional no es tan importante como en el pasado. ^[6]

Sin embargo, para cualquier modelo no lineal (por ejemplo, los modelos Logit y Probit ), la heterocedasticidad tiene consecuencias más graves: las estimaciones de máxima verosimilitud (MLE) de los parámetros normalmente estarán sesgadas, así como inconsistentes (a menos que la función de verosimilitud se modifique para tener en cuenta correctamente la forma precisa de heterocedasticidad o la distribución sea miembro de la familia exponencial lineal y la función de expectativa condicional se especifique correctamente). ^{[14] [15]} Sin embargo, en el contexto de los modelos de elección binaria ( Logit o Probit ), la heterocedasticidad solo dará como resultado un efecto de escala positivo en la media asintótica de la MLE mal especificada (es decir, el modelo que ignora la heterocedasticidad). ^[16] Como resultado, las predicciones que se basan en la MLE mal especificada seguirán siendo correctas. Además, la MLE Probit y Logit mal especificada se distribuirá normalmente de forma asintótica, lo que permite realizar las pruebas de significancia habituales (con la matriz de varianza-covarianza adecuada). Sin embargo, en lo que respecta a la prueba de hipótesis general, como señala Greene , "el simple cálculo de una matriz de covarianza robusta para un estimador que de otro modo sería inconsistente no le otorga redención. En consecuencia, la virtud de una matriz de covarianza robusta en este contexto no está clara". ^[17]

Corrección

Existen varias correcciones comunes para la heterocedasticidad, que son:

• Una transformación estabilizadora de los datos, por ejemplo, datos logaritmizados . Las series no logaritmizadas que crecen exponencialmente a menudo parecen tener una variabilidad creciente a medida que la serie aumenta con el tiempo. Sin embargo, la variabilidad en términos porcentuales puede ser bastante estable.
• Utilice una especificación diferente para el modelo (diferentes variables X , o quizás transformaciones no lineales de las variables X ).
• Aplicar un método de estimación de mínimos cuadrados ponderados , en el que se aplican MCO a los valores transformados o ponderados de X e Y. Los pesos varían a lo largo de las observaciones, generalmente dependiendo de las varianzas de error cambiantes. En una variación, los pesos están directamente relacionados con la magnitud de la variable dependiente, y esto corresponde a la regresión porcentual de mínimos cuadrados. ^[18]
• Los errores estándar consistentes con la heterocedasticidad (HCSE), aunque siguen siendo sesgados, mejoran las estimaciones de MCO. ^[2] HCSE es un estimador consistente de errores estándar en modelos de regresión con heterocedasticidad. Este método corrige la heterocedasticidad sin alterar los valores de los coeficientes. Este método puede ser superior al MCO regular porque si hay heterocedasticidad la corrige, sin embargo, si los datos son homocedásticos, los errores estándar son equivalentes a los errores estándar convencionales estimados por MCO. Se han propuesto varias modificaciones del método de White para calcular errores estándar consistentes con la heterocedasticidad como correcciones con propiedades superiores para muestras finitas.
• El bootstrap salvaje se puede utilizar como un método de remuestreo que respeta las diferencias en la varianza condicional del término de error. Una alternativa es remuestrear las observaciones en lugar de los errores. Tenga en cuenta que el remuestreo de errores sin respetar los valores afiliados de la observación impone homocedasticidad y, por lo tanto, produce una inferencia incorrecta.
• Utilice MINQUE o incluso los estimadores habituales (para muestras independientes con observaciones cada una), cuyas pérdidas de eficiencia no son sustanciales cuando el número de observaciones por muestra es grande ( ), especialmente para un número pequeño de muestras independientes. ^[19] ${\textstyle s_{i}^{2}=(n_{i}-1)^{-1}\sum _{j}\left(y_{ij}-{\bar {y}}_{i}\right)^{2}}$ ${\displaystyle i=1,2,...,k}$ ${\displaystyle j=1,2,...,n_{i}}$ ${\displaystyle n_{i}>5}$

Pruebas

Valor absoluto de los residuos para datos heterocedásticos de primer orden simulados

Los residuos se pueden probar para homocedasticidad utilizando la prueba de Breusch-Pagan , ^[20] que realiza una regresión auxiliar de los residuos al cuadrado sobre las variables independientes. A partir de esta regresión auxiliar, se conserva la suma explicada de los cuadrados, se divide por dos y luego se convierte en la estadística de prueba para una distribución de chi-cuadrado con los grados de libertad iguales al número de variables independientes. ^[21] La hipótesis nula de esta prueba de chi-cuadrado es homocedasticidad, y la hipótesis alternativa indicaría heterocedasticidad. Dado que la prueba de Breusch-Pagan es sensible a las desviaciones de la normalidad o tamaños de muestra pequeños, la prueba de Koenker-Bassett o "Breusch-Pagan generalizada" se utiliza comúnmente en su lugar. ^{[22] [ cita(s) adicional(es) necesaria(s) ]} A partir de la regresión auxiliar, se conserva el valor R-cuadrado que luego se multiplica por el tamaño de la muestra y luego se convierte en la estadística de prueba para una distribución de chi-cuadrado (y utiliza los mismos grados de libertad). Aunque no es necesario para la prueba de Koenker-Bassett, la prueba de Breusch-Pagan requiere que los residuos al cuadrado también se dividan por la suma de los cuadrados de los residuos dividida por el tamaño de la muestra. ^[22] La prueba de heterocedasticidad por grupo se puede realizar con la prueba de Goldfeld-Quandt . ^[23]

Debido al uso estándar de errores estándar consistentes con la heterocedasticidad y al problema de la prueba previa , hoy en día los econometristas rara vez utilizan pruebas para heterocedasticidad condicional. ^[6]

Lista de pruebas

Aunque las pruebas de heterocedasticidad entre grupos pueden considerarse formalmente como un caso especial de pruebas dentro de modelos de regresión, algunas pruebas tienen estructuras específicas para este caso.

Pruebas en regresión

• Prueba de Goldfeld-Quandt
• Prueba de estacionamiento ^[24]
• Prueba de Glejser ^{[25] [26]}
• Prueba de Harrison-McCabe
• Prueba de Breusch-Pagan
• Prueba blanca ^[2]
• Prueba de Cook-Weisberg

Pruebas para datos agrupados

• Prueba F de igualdad de varianzas
• Prueba C de Cochran
• Prueba de Hartley
• Prueba de Bartlett
• Prueba de Levene
• Prueba de Brown-Forsythe

Generalizaciones

Distribuciones homocedásticas

Dos o más distribuciones normales son homocedásticas y carecen de correlación serial si comparten las mismas diagonales en su matriz de covarianza y sus entradas no diagonales son cero. Las distribuciones homocedásticas son especialmente útiles para derivar algoritmos de reconocimiento de patrones estadísticos y de aprendizaje automático . Un ejemplo popular de un algoritmo que asume homocedasticidad es el análisis discriminante lineal de Fisher . El concepto de homocedasticidad se puede aplicar a distribuciones en esferas. ^[27] ${\displaystyle N(\mu _{1},\Sigma _{1}),N(\mu _{2},\Sigma _{2}),}$ ${\displaystyle \Sigma _{1}{ii}=\Sigma _{2}{jj},\ \forall i=j.}$

Datos multivariados

El estudio de la homecedasticidad y la heterocedasticidad se ha generalizado al caso multivariado, que trata con las covarianzas de las observaciones vectoriales en lugar de la varianza de las observaciones escalares. Una versión de esto es utilizar matrices de covarianza como medida multivariada de dispersión. Varios autores han considerado pruebas en este contexto, tanto para situaciones de regresión como de datos agrupados. ^{[28] [29]} La prueba de Bartlett para heterocedasticidad entre datos agrupados, utilizada más comúnmente en el caso univariado, también se ha extendido para el caso multivariado, pero solo existe una solución manejable para 2 grupos. ^[30] Existen aproximaciones para más de dos grupos, y ambas se denominan prueba M de Box .

Véase también

• Heterogeneidad
• Error esférico
• Errores estándar consistentes con la heterocedasticidad

Referencias

1. Para la etimología griega del término, véase McCulloch, J. Huston (1985). "On Heteros*edasticity". Econometrica . 53 (2): 483. JSTOR  1911250.
2. White, Halbert (1980). "Un estimador de matriz de covarianza consistente con la heterocedasticidad y una prueba directa de heterocedasticidad". Econometrica . 48 (4): 817–838. CiteSeerX 10.1.1.11.7646 . doi :10.2307/1912934. JSTOR  1912934.  
3. Gujarati, DN; Porter, DC (2009). Econometría básica (quinta edición). Boston: McGraw-Hill Irwin. pág. 400. ISBN  9780073375779.
4. Goldberger, Arthur S. (1964). Teoría econométrica . Nueva York: John Wiley & Sons. pp. 238–243. ISBN 9780471311010.
5. Johnston, J. (1972). Métodos econométricos . Nueva York: McGraw-Hill. págs. 214-221.
6. Angrist, Joshua D.; Pischke, Jörn-Steffen (31 de diciembre de 2009). Econometría casi inofensiva: un compañero empirista. Princeton University Press. doi :10.1515/9781400829828. ISBN 978-1-4008-2982-8.
7. Long, J. Scott ; Trivedi, Pravin K. (1993). "Algunas pruebas de especificación para el modelo de regresión lineal". En Bollen, Kenneth A.; Long, J. Scott (eds.). Pruebas de modelos de ecuaciones estructurales . Londres: Sage. págs. 66–110. ISBN 978-0-8039-4506-7.
8. Engle, Robert F. (julio de 1982). "Heteroscedasticidad condicional autorregresiva con estimaciones de la varianza de la inflación del Reino Unido". Econometrica . 50 (4): 987–1007. doi :10.2307/1912773. ISSN  0012-9682. JSTOR  1912773.
9. Peter Kennedy, A Guide to Econometrics , 5.ª edición, pág. 137.
10. Jinadasa, Gamage; Weerahandi, Sam (1998). "Rendimiento de tamaño de algunas pruebas en ANOVA unidireccional". Comunicaciones en Estadística - Simulación y Computación . 27 (3): 625. doi :10.1080/03610919808813500.
11. Bathke, A (2004). "La prueba ANOVA F todavía se puede utilizar en algunos diseños balanceados con varianzas desiguales y datos no normales". Journal of Statistical Planning and Inference . 126 (2): 413–422. doi :10.1016/j.jspi.2003.09.010.
12. Fox, J. (1997). Análisis de regresión aplicado, modelos lineales y métodos relacionados . California: Sage Publications. pág. 306.(Citado en Gujarati et al. 2009, pág. 400)
13. Mankiw, NG (1990). "Un curso rápido de actualización en macroeconomía". Revista de literatura económica . 28 (4): 1645–1660 [p. 1648]. doi : 10.3386/w3256 . JSTOR  2727441.
14. Giles, Dave (8 de mayo de 2013). "Errores estándar robustos para modelos no lineales". Econometrics Beat .
15. Gourieroux, C.; Monfort, A.; Trognon, A. (1984). "Métodos de pseudomáxima verosimilitud: teoría". Econometrica . 52 (3): 681–700. doi :10.2307/1913471. ISSN  0012-9682.
16. Ginker, T.; Lieberman, O. (2017). "Robustez de los modelos de elección binaria a la heterocedasticidad condicional". Economics Letters . 150 : 130–134. doi :10.1016/j.econlet.2016.11.024.
17. Greene, William H. (2012). "Estimación e inferencia en modelos de elección binaria". Análisis econométrico (séptima edición). Boston: Pearson Education. pp. 730–755 [p. 733]. ISBN 978-0-273-75356-8.
18. Tofallis, C (2008). "Regresión porcentual de mínimos cuadrados". Revista de métodos estadísticos aplicados modernos . 7 : 526–534. doi :10.2139/ssrn.1406472. SSRN  1406472.
19. JNK Rao (marzo de 1973). "Sobre la estimación de varianzas heterocedásticas". Biometrics . 29 (1): 11–24. doi :10.2307/2529672. JSTOR  2529672.
20. Breusch, TS; Pagan, AR (1979). "Una prueba simple para heteroscedasticidad y variación aleatoria de coeficientes". Econometrica . 47 (5): 1287–1294. doi :10.2307/1911963. ISSN  0012-9682. JSTOR  1911963.
21. Ullah, Muhammad Imdad (26 de julio de 2012). "Prueba pagana de Breusch para heterocedasticidad". Estadística básica y análisis de datos . Consultado el 28 de noviembre de 2020 .
22. Pryce, Gwilym. "Heteroscedasticidad: prueba y corrección en SPSS" (PDF) . págs. 12–18. Archivado (PDF) desde el original el 27 de marzo de 2017. Consultado el 26 de marzo de 2017 .
23. Baum, Christopher F. (2006). "Stata Tip 38: Testing for Groupwise Heteroscedasticity" (Consejo 38 de Stata: Pruebas de heterocedasticidad grupal). The Stata Journal: Promoción de las comunicaciones sobre estadística y Stata . 6 (4): 590–592. doi : 10.1177/1536867X0600600412 . ISSN  1536-867X. S2CID  : 117349246.
24. RE Park (1966). "Estimación con términos de error heterocedástico". Econometrica . 34 (4): 888. doi :10.2307/1910108. JSTOR  1910108.
25. Glejser, H. (1969). "Una nueva prueba de heterocedasticidad". Revista de la Asociación Estadounidense de Estadística . 64 (325): 316–323. doi :10.1080/01621459.1969.10500976.
26. Machado, José AF; Silva, JMC Santos (2000). "Revisión de la prueba de Glejser". Revista de Econometría . 97 (1): 189–202. doi :10.1016/S0304-4076(00)00016-6.
27. Hamsici, Onur C.; Martinez, Aleix M. (2007) "Distribuciones esféricas-homocedásticas: la equivalencia de distribuciones esféricas y normales en la clasificación", Journal of Machine Learning Research , 8, 1583-1623
28. Holgersson, HET; Shukur, G. (2004). "Prueba de heterocedasticidad multivariante". Revista de computación estadística y simulación . 74 (12): 879. doi :10.1080/00949650410001646979. hdl : 2077/24416 . S2CID :  121576769.
29. Gupta, AK; Tang, J. (1984). "Distribución de la estadística de razón de verosimilitud para probar la igualdad de matrices de covarianza de modelos gaussianos multivariados". Biometrika . 71 (3): 555–559. doi :10.1093/biomet/71.3.555. JSTOR  2336564.
30. d'Agostino, RB; Russell, HK (2005). "Prueba de Bartlett multivariante". Enciclopedia de bioestadística . doi :10.1002/0470011815.b2a13048. ISBN . 978-0470849071.

Lectura adicional

La mayoría de los libros de texto de estadística incluyen al menos algún material sobre homocedasticidad y heterocedasticidad. Algunos ejemplos son:

• Asteriou, Dimitros; Hall, Stephen G. (2011). Econometría aplicada (segunda edición). Palgrave MacMillan. págs. 109–147. ISBN 978-0-230-27182-1.
• Davidson, Russell; MacKinnon, James G. (1993). Estimación e inferencia en econometría. Nueva York: Oxford University Press. pp. 547–582. ISBN 978-0-19-506011-9.
• Dougherty, Christopher (2011). Introducción a la econometría. Nueva York: Oxford University Press. pp. 280–299. ISBN 978-0-19-956708-9.
• Gujarati, Damodar N. ; Porter, Dawn C. (2009). Econometría básica (quinta edición). Nueva York: McGraw-Hill Irwin. págs. 365–411. ISBN 978-0-07-337577-9.
• Kmenta, Jan (1986). Elementos de econometría (segunda edición). Nueva York: Macmillan. Págs. 269-298. ISBN. 978-0-02-365070-3.
• Maddala, GS ; Lahiri, Kajal (2009). Introducción a la econometría (cuarta edición). Nueva York: Wiley. pp. 211–238. ISBN 978-0-470-01512-4.

Enlaces externos

• Conferencia sobre econometría (tema: heterocedasticidad) en YouTube por Mark Thoma