Mínimos cuadrados ordinarios

Método para estimar los parámetros desconocidos en un modelo de regresión lineal.

En estadística , los mínimos cuadrados ordinarios ( OLS ) son un tipo de método de mínimos cuadrados lineales para elegir los parámetros desconocidos en un modelo de regresión lineal (con efectos fijos de nivel uno ^{[ aclaración necesaria ] de una} función lineal de un conjunto de variables explicativas ) mediante el principio de mínimos cuadrados : minimizar la suma de los cuadrados de las diferencias entre la variable dependiente observada (valores de la variable que se observa) en el conjunto de datos de entrada y la salida de la función (lineal) de la variable independiente .

Geométricamente, esto se ve como la suma de las distancias al cuadrado, paralelas al eje de la variable dependiente, entre cada punto de datos del conjunto y el punto correspondiente en la superficie de regresión: cuanto más pequeñas sean las diferencias, mejor se ajusta el modelo a los datos. . El estimador resultante se puede expresar mediante una fórmula simple, especialmente en el caso de una regresión lineal simple , en la que hay un único regresor en el lado derecho de la ecuación de regresión.

El estimador MCO es consistente para los efectos fijos de nivel uno cuando los regresores son exógenos y forma una colinealidad perfecta (condición de rango), consistente para la estimación de la varianza de los residuos cuando los regresores tienen cuartos momentos finitos ^[1] y, según el método de Gauss-Markov teorema : óptimo en la clase de estimadores lineales insesgados cuando los errores son homocedásticos y no correlacionados en serie . En estas condiciones, el método de MCO proporciona una estimación insesgada de media de varianza mínima cuando los errores tienen varianzas finitas . Bajo el supuesto adicional de que los errores se distribuyen normalmente con media cero, MCO es el estimador de máxima verosimilitud que supera a cualquier estimador insesgado no lineal.

Modelo lineal

La ley de Okun en macroeconomía establece que en una economía el crecimiento del PIB debería depender linealmente de los cambios en la tasa de desempleo. Aquí se utiliza el método de mínimos cuadrados ordinarios para construir la recta de regresión que describe esta ley.

Supongamos que los datos consisten en observaciones . Cada observación incluye una respuesta escalar y un vector de columna de parámetros (regresores), es decir, . En un modelo de regresión lineal , la variable de respuesta , es una función lineal de los regresores: ${\displaystyle n}$ ${\displaystyle \left\{\mathbf {x} _{i},y_{i}\right\}_{i=1}^{n}}$ ${\displaystyle i}$ ${\displaystyle y_{i}}$ ${\displaystyle \mathbf {x} _{i}}$ ${\displaystyle p}$ ${\displaystyle \mathbf {x} _{i}=\left[x_{i1},x_{i2},\dots ,x_{ip}\right]^{\operatorname {T} }}$ ${\displaystyle y_{i}}$

${\displaystyle y_{i}=\beta _{1}\ x_{i1}+\beta _{2}\ x_{i2}+\cdots +\beta _{p}\ x_{ip}+\varepsilon _{i},}$

o en forma vectorial ,

${\displaystyle y_{i}=\mathbf {x} _{i}^{\operatorname {T} }{\boldsymbol {\beta }}+\varepsilon _{i},\,}$

donde , como se introdujo anteriormente, es un vector columna de la -ésima observación de todas las variables explicativas; es un vector de parámetros desconocidos; y el escalar representa variables aleatorias no observadas ( errores ) de la -ésima observación. Tiene en cuenta las influencias sobre las respuestas provenientes de fuentes distintas a las variables explicativas . Este modelo también se puede escribir en notación matricial como ${\displaystyle \mathbf {x} _{i}}$ ${\displaystyle i}$ ${\displaystyle {\boldsymbol {\beta }}}$ ${\displaystyle p\times 1}$ ${\displaystyle \varepsilon _{i}}$ ${\displaystyle i}$ ${\displaystyle \varepsilon _{i}}$ ${\displaystyle y_{i}}$ ${\displaystyle \mathbf {x} _{i}}$

${\displaystyle \mathbf {y} =\mathbf {X} {\boldsymbol {\beta }}+{\boldsymbol {\varepsilon }},\,}$

donde y son vectores de las variables de respuesta y de los errores de las observaciones, y es una matriz de regresores, también llamada a veces matriz de diseño , cuya fila es y contiene las -ésimas observaciones de todas las variables explicativas. ${\displaystyle \mathbf {y} }$ ${\displaystyle {\boldsymbol {\varepsilon }}}$ ${\displaystyle n\times 1}$ ${\displaystyle n}$ ${\displaystyle \mathbf {X} }$ ${\displaystyle n\times p}$ ${\displaystyle i}$ ${\displaystyle \mathbf {x} _{i}^{\operatorname {T} }}$ ${\displaystyle i}$

Normalmente, se incluye un término constante en el conjunto de regresores , por ejemplo, tomando para todos . El coeficiente correspondiente a este regresor se llama intercepto . Sin la intersección, la línea ajustada se ve obligada a cruzar el origen cuando . ${\displaystyle \mathbf {X} }$ ${\displaystyle x_{i1}=1}$ ${\displaystyle i=1,\dots ,n}$ ${\displaystyle \beta _{1}}$ ${\displaystyle x_{i}={\vec {0}}}$

Los regresores no tienen que ser independientes para que la estimación sea consistente, pero la multicolinealidad hace que la estimación sea inconsistente. Como ejemplo concreto en el que los regresores no son independientes, podríamos sospechar que la respuesta depende linealmente tanto de un valor como de su cuadrado; en cuyo caso incluiríamos un regresor cuyo valor sea simplemente el cuadrado de otro regresor. En ese caso, el modelo sería cuadrático en el segundo regresor, pero aun así se considera un modelo lineal porque el modelo sigue siendo lineal en los parámetros ( ). ${\displaystyle {\boldsymbol {\beta }}}$

Formulación matricial/vectorial

Considere un sistema sobredeterminado

${\displaystyle \sum _{j=1}^{p}x_{ij}\beta _{j}=y_{i},\ (i=1,2,\dots ,n),}$

de ecuaciones lineales en coeficientes desconocidos , , con . Esto se puede escribir en forma matricial como ${\displaystyle n}$ ${\displaystyle p}$ ${\displaystyle \beta _{1},\beta _{2},\dots ,\beta _{p}}$ ${\displaystyle n>p}$

${\displaystyle \mathbf {X} {\boldsymbol {\beta }}=\mathbf {y} ,}$

dónde

${\displaystyle \mathbf {X} ={\begin{bmatrix}X_{11}&X_{12}&\cdots &X_{1p}\\X_{21}&X_{22}&\cdots &X_{2p}\\\vdots &\vdots &\ddots &\vdots \\X_{n1}&X_{n2}&\cdots &X_{np}\end{bmatrix}},\qquad {\boldsymbol {\beta }}={\begin{bmatrix}\beta _{1}\\\beta _{2}\\\vdots \\\beta _{p}\end{bmatrix}},\qquad \mathbf {y} ={\begin{bmatrix}y_{1}\\y_{2}\\\vdots \\y_{n}\end{bmatrix}}.}$

(Nota: para un modelo lineal como el anterior, no todos los elementos contienen información sobre los puntos de datos. La primera columna se completa con unos. Solo las otras columnas contienen datos reales. Entonces, aquí es igual al número de regresores más uno) . ${\displaystyle \mathbf {X} }$ ${\displaystyle X_{i1}=1}$ ${\displaystyle p}$

Un sistema de este tipo generalmente no tiene una solución exacta, por lo que el objetivo es encontrar los coeficientes que se ajusten "mejor" a las ecuaciones, en el sentido de resolver el problema de minimización cuadrática. ${\displaystyle {\boldsymbol {\beta }}}$

${\displaystyle {\hat {\boldsymbol {\beta }}}={\underset {\boldsymbol {\beta }}{\operatorname {arg\,min} }}\,S({\boldsymbol {\beta }}),}$

donde la función objetivo está dada por ${\displaystyle S}$

${\displaystyle S({\boldsymbol {\beta }})=\sum _{i=1}^{n}\left|y_{i}-\sum _{j=1}^{p}X_{ij}\beta _{j}\right|^{2}=\left\|\mathbf {y} -\mathbf {X} {\boldsymbol {\beta }}\right\|^{2}.}$

Una justificación para elegir este criterio se proporciona en Propiedades a continuación. Este problema de minimización tiene solución única, siempre que las columnas de la matriz sean linealmente independientes , dada resolviendo las llamadas ecuaciones normales : ${\displaystyle p}$ ${\displaystyle \mathbf {X} }$

${\displaystyle \left(\mathbf {X} ^{\operatorname {T} }\mathbf {X} \right){\hat {\boldsymbol {\beta }}}=\mathbf {X} ^{\operatorname {T} }\mathbf {y} \ .}$

La matriz se conoce como matriz normal o matriz de Gram y la matriz se conoce como matriz de momento de regresor por regresores. ^[2] Finalmente, es el vector de coeficientes del hiperplano de mínimos cuadrados , expresado como ${\displaystyle \mathbf {X} ^{\operatorname {T} }\mathbf {X} }$ ${\displaystyle \mathbf {X} ^{\operatorname {T} }\mathbf {y} }$ ${\displaystyle {\hat {\boldsymbol {\beta }}}}$

${\displaystyle {\hat {\boldsymbol {\beta }}}=\left(\mathbf {X} ^{\operatorname {T} }\mathbf {X} \right)^{-1}\mathbf {X} ^{\operatorname {T} }\mathbf {y} .}$

o

${\displaystyle {\hat {\boldsymbol {\beta }}}={\boldsymbol {\beta }}+\left(\mathbf {X} ^{\operatorname {T} }\mathbf {X} \right)^{-1}\mathbf {X} ^{\operatorname {T} }{\boldsymbol {\varepsilon }}.}$

Estimacion

Supongamos que b es un valor "candidato" para el vector de parámetros β . La cantidad y _i − x _i ^T b , llamada residual para la i -ésima observación, mide la distancia vertical entre el punto de datos ( x _i , y _i ) y el hiperplano y = x ^T b , y así evalúa el grado de ajuste entre los datos reales y el modelo. La suma de cuadrados residuales ( SSR ) (también llamada suma de cuadrados de error ( ESS ) o suma de cuadrados residual ( RSS )) ^[3] es una medida del ajuste general del modelo:

${\displaystyle S(b)=\sum _{i=1}^{n}(y_{i}-x_{i}^{\operatorname {T} }b)^{2}=(y-Xb)^{\operatorname {T} }(y-Xb),}$

donde T denota la transpuesta de la matriz , y las filas de X , que denotan los valores de todas las variables independientes asociadas con un valor particular de la variable dependiente, son X i ₌ x _i ^T. El valor de b que minimiza esta suma se llama estimador MCO para β . La función S ( b ) es cuadrática en b con hessiano definido positivo y, por lo tanto, esta función posee un mínimo global único en , que puede estar dado por la fórmula explícita: ^{[4] [prueba]} ${\displaystyle b={\hat {\beta }}}$

${\displaystyle {\hat {\beta }}=\operatorname {argmin} _{b\in \mathbb {R} ^{p}}S(b)=(X^{\operatorname {T} }X)^{-1}X^{\operatorname {T} }y\ .}$

El producto N = X ^T X es una matriz de Gram y su inversa, Q = N ^–1 , es la matriz cofactor de β , ^{[5] [6] [7]} estrechamente relacionada con su matriz de covarianza, C _β . La matriz ( X ^T X ) ^–1 X ^T = Q X ^T se llama matriz pseudoinversa de Moore-Penrose de X. Esta formulación resalta el punto de que la estimación se puede llevar a cabo si, y sólo si, no existe una multicolinealidad perfecta entre las variables explicativas (lo que haría que la matriz de gramos no tuviera inversa).

Después de haber estimado β , los valores ajustados (o valores predichos ) de la regresión serán

${\displaystyle {\hat {y}}=X{\hat {\beta }}=Py,}$

donde P = X ( X ^T X ) ⁻¹ X ^T es la matriz de proyección sobre el espacio V atravesado por las columnas de X . Esta matriz P también se denomina a veces matriz de sombrero porque "pone un sombrero" a la variable y . Otra matriz, estrechamente relacionada con P es la matriz aniquiladora M = In ₋ P ; esta es una matriz de proyección en el espacio ortogonal a V . Ambas matrices P y M son simétricas e idempotentes (lo que significa que P ² = P y M ² = M ) y se relacionan con la matriz de datos X a través de las identidades PX = X y MX = 0 . ^[8] La Matriz M crea los residuos de la regresión:

${\displaystyle {\hat {\varepsilon }}=y-{\hat {y}}=y-X{\hat {\beta }}=My=M(X\beta +\varepsilon )=(MX)\beta +M\varepsilon =M\varepsilon .}$

Usando estos residuos podemos estimar el valor de σ ² usando el estadístico chi-cuadrado reducido :

${\displaystyle s^{2}={\frac {{\hat {\varepsilon }}^{\mathrm {T} }{\hat {\varepsilon }}}{n-p}}={\frac {(My)^{\mathrm {T} }My}{n-p}}={\frac {y^{\mathrm {T} }M^{\mathrm {T} }My}{n-p}}={\frac {y^{\mathrm {T} }My}{n-p}}={\frac {S({\hat {\beta }})}{n-p}},\qquad {\hat {\sigma }}^{2}={\frac {n-p}{n}}\;s^{2}}$

El denominador, n − p , son los grados de libertad estadísticos . La primera cantidad, s ² , es la estimación MCO para σ ² , mientras que la segunda , es la estimación MLE para σ ² . Los dos estimadores son bastante similares en muestras grandes; el primer estimador siempre es insesgado , mientras que el segundo estimador está sesgado pero tiene un error cuadrático medio menor . En la práctica, s ² se utiliza con más frecuencia, ya que es más conveniente para la prueba de hipótesis. La raíz cuadrada de s ² se llama error estándar de regresión , ^[9] error estándar de la regresión , ^{[10] [11]} o error estándar de la ecuación . ^[8] ${\displaystyle \scriptstyle {\hat {\sigma }}^{2}}$

Es común evaluar la bondad de ajuste de la regresión MCO comparando cuánto se puede reducir la variación inicial en la muestra al regresar a X. El coeficiente de determinación R ² se define como una relación entre la varianza "explicada" y la varianza "total" de la variable dependiente y , en los casos en que la suma de cuadrados de la regresión es igual a la suma de cuadrados de los residuos: ^[12]

${\displaystyle R^{2}={\frac {\sum ({\hat {y}}_{i}-{\overline {y}})^{2}}{\sum (y_{i}-{\overline {y}})^{2}}}={\frac {y^{\mathrm {T} }P^{\mathrm {T} }LPy}{y^{\mathrm {T} }Ly}}=1-{\frac {y^{\mathrm {T} }My}{y^{\mathrm {T} }Ly}}=1-{\frac {\rm {RSS}}{\rm {TSS}}}}$

donde TSS es la suma total de cuadrados de la variable dependiente, y es una matriz de unos de n × n . ( es una matriz de centrado que equivale a la regresión sobre una constante; simplemente resta la media de una variable). Para que R ² sea significativo, la matriz X de datos sobre regresores debe contener un vector columna de unos para representar la constante cuyo coeficiente es el intercepto de la regresión. En ese caso, R ² siempre será un número entre 0 y 1, donde valores cercanos a 1 indican un buen grado de ajuste. ${\textstyle L=I_{n}-{\frac {1}{n}}J_{n}}$ ${\textstyle J_{n}}$ ${\displaystyle L}$

La varianza en la predicción de la variable independiente en función de la variable dependiente se da en el artículo Mínimos cuadrados polinomiales .

Modelo de regresión lineal simple

Si la matriz de datos X contiene sólo dos variables, una constante y un regresor escalar x _i , entonces esto se denomina "modelo de regresión simple". Este caso se considera a menudo en las clases de estadística para principiantes, ya que proporciona fórmulas mucho más simples, incluso adecuadas para el cálculo manual. Los parámetros se denotan comúnmente como ( α , β ) :

${\displaystyle y_{i}=\alpha +\beta x_{i}+\varepsilon _{i}.}$

Las estimaciones de mínimos cuadrados en este caso vienen dadas por fórmulas simples

${\displaystyle {\begin{aligned}{\widehat {\beta }}&={\frac {\sum _{i=1}^{n}{(x_{i}-{\bar {x}})(y_{i}-{\bar {y}})}}{\sum _{i=1}^{n}{(x_{i}-{\bar {x}})^{2}}}}\\[2pt]{\widehat {\alpha }}&={\bar {y}}-{\widehat {\beta }}\,{\bar {x}}\ ,\end{aligned}}}$

Derivaciones alternativas

En el apartado anterior se obtuvo el estimador de mínimos cuadrados como un valor que minimiza la suma de residuos al cuadrado del modelo. Sin embargo, también es posible derivar el mismo estimador a partir de otros enfoques. En todos los casos, la fórmula del estimador MCO sigue siendo la misma: ^{^} β = ( X ^T X ) ⁻¹ X ^T y ; la única diferencia está en cómo interpretamos este resultado. ${\displaystyle {\hat {\beta }}}$

Proyección

La estimación MCO puede verse como una proyección sobre el espacio lineal abarcado por los regresores. (Aquí cada uno de y se refiere a una columna de la matriz de datos). ${\displaystyle X_{1}}$ ${\displaystyle X_{2}}$

Para los matemáticos, MCO es una solución aproximada a un sistema sobredeterminado de ecuaciones lineales Xβ ≈ y , donde β es la incógnita. Suponiendo que el sistema no se puede resolver exactamente (el número de ecuaciones n es mucho mayor que el número de incógnitas p ), buscamos una solución que pueda proporcionar la discrepancia más pequeña entre los lados derecho e izquierdo. En otras palabras, buscamos la solución que satisfaga

${\displaystyle {\hat {\beta }}={\rm {arg}}\min _{\beta }\,\lVert \mathbf {y} -\mathbf {X} {\boldsymbol {\beta }}\rVert ,}$

donde ‖ · ‖ es la  norma estándar L 2 en el espacio euclidiano de n dimensiones R ⁿ . La cantidad predicha Xβ es simplemente una determinada combinación lineal de los vectores de regresores. Por lo tanto, el vector residual y − Xβ tendrá la longitud más pequeña cuando y se proyecte ortogonalmente sobre el subespacio lineal abarcado por las columnas de X. El estimador MCO en este caso se puede interpretar como los coeficientes de descomposición vectorial de ^{^} y = Py a lo largo de la base de X. ${\displaystyle {\hat {\beta }}}$

En otras palabras, las ecuaciones de gradiente mínimo se pueden escribir como:

${\displaystyle (\mathbf {y} -\mathbf {X} {\hat {\boldsymbol {\beta }}})^{\top }\mathbf {X} =0.}$

Una interpretación geométrica de estas ecuaciones es que el vector de residuos es ortogonal al espacio columna de X , ya que el producto escalar es igual a cero para cualquier vector conforme, v . Esto significa que es el más corto de todos los vectores posibles , es decir, la varianza de los residuales es la mínima posible. Esto se ilustra a la derecha. ${\displaystyle \mathbf {y} -X{\hat {\boldsymbol {\beta }}}}$ ${\displaystyle (\mathbf {y} -\mathbf {X} {\hat {\boldsymbol {\beta }}})\cdot \mathbf {X} \mathbf {v} }$ ${\displaystyle \mathbf {y} -\mathbf {X} {\boldsymbol {\hat {\beta }}}}$ ${\displaystyle \mathbf {y} -\mathbf {X} {\boldsymbol {\beta }}}$

Introduciendo y una matriz K con el supuesto de que una matriz no es singular y K ^T X = 0 (cf. Proyecciones ortogonales ), el vector residual debe satisfacer la siguiente ecuación: ${\displaystyle {\hat {\boldsymbol {\gamma }}}}$ ${\displaystyle [\mathbf {X} \ \mathbf {K} ]}$

${\displaystyle {\hat {\mathbf {r} }}:=\mathbf {y} -\mathbf {X} {\hat {\boldsymbol {\beta }}}=\mathbf {K} {\hat {\boldsymbol {\gamma }}}.}$

La ecuación y la solución de mínimos cuadrados lineales se describen a continuación:

${\displaystyle {\begin{aligned}\mathbf {y} &={\begin{bmatrix}\mathbf {X} &\mathbf {K} \end{bmatrix}}{\begin{bmatrix}{\hat {\boldsymbol {\beta }}}\\{\hat {\boldsymbol {\gamma }}}\end{bmatrix}},\\{}\Rightarrow {\begin{bmatrix}{\hat {\boldsymbol {\beta }}}\\{\hat {\boldsymbol {\gamma }}}\end{bmatrix}}&={\begin{bmatrix}\mathbf {X} &\mathbf {K} \end{bmatrix}}^{-1}\mathbf {y} ={\begin{bmatrix}\left(\mathbf {X} ^{\top }\mathbf {X} \right)^{-1}\mathbf {X} ^{\top }\\\left(\mathbf {K} ^{\top }\mathbf {K} \right)^{-1}\mathbf {K} ^{\top }\end{bmatrix}}\mathbf {y} .\end{aligned}}}$

Otra forma de verlo es considerar que la línea de regresión es un promedio ponderado de las líneas que pasan por la combinación de dos puntos cualesquiera en el conjunto de datos. ^[13] Aunque esta forma de cálculo es más costosa desde el punto de vista computacional, proporciona una mejor intuición en OLS.

Máxima verosimilitud

El estimador MCO es idéntico al estimador de máxima verosimilitud (MLE) bajo el supuesto de normalidad para los términos de error. ^{[14] [prueba]} Este supuesto de normalidad tiene importancia histórica, ya que proporcionó la base para los primeros trabajos en análisis de regresión lineal de Yule y Pearson . ^{[ cita necesaria ]} A partir de las propiedades de MLE, podemos inferir que el estimador MCO es asintóticamente eficiente (en el sentido de alcanzar el límite de Cramér-Rao para la varianza) si se satisface el supuesto de normalidad. ^[15]

Método generalizado de momentos.

En el caso de iid , el estimador MCO también puede verse como un estimador GMM que surge de las condiciones de momento.

${\displaystyle \mathrm {E} {\big [}\,x_{i}\left(y_{i}-x_{i}^{\operatorname {T} }\beta \right)\,{\big ]}=0.}$

Estas condiciones de momento establecen que los regresores no deben estar correlacionados con los errores. Dado que x _i es un p -vector, el número de condiciones de momento es igual a la dimensión del vector de parámetros β y, por tanto, el sistema se identifica exactamente. Este es el llamado caso clásico de GMM, cuando el estimador no depende de la elección de la matriz de ponderación.

Tenga en cuenta que el supuesto original de exogeneidad estricta E[ ε _i  |  x _i ] = 0 implica un conjunto de condiciones de momento mucho más rico que el indicado anteriormente. En particular, este supuesto implica que para cualquier función vectorial ƒ , se cumplirá la condición de momento E[ ƒ ( x _i )· ε _i ] = 0 . Sin embargo, se puede demostrar utilizando el teorema de Gauss-Markov que la elección óptima de la función ƒ es tomar ƒ ( x ) = x , lo que da como resultado la ecuación de momento publicada anteriormente.

Propiedades

Suposiciones

Existen varios marcos diferentes en los que se puede formular el modelo de regresión lineal para que la técnica OLS sea aplicable. Cada una de estas configuraciones produce las mismas fórmulas y los mismos resultados. La única diferencia es la interpretación y los supuestos que deben imponerse para que el método dé resultados significativos. La elección del marco aplicable depende principalmente de la naturaleza de los datos disponibles y de la tarea de inferencia que debe realizarse.

Una de las líneas de diferencia en la interpretación es si se deben tratar los regresores como variables aleatorias o como constantes predefinidas. En el primer caso ( diseño aleatorio ) , los regresores x _i son aleatorios y se muestrean junto con los y _i de alguna población , como en un estudio observacional . Este enfoque permite un estudio más natural de las propiedades asintóticas de los estimadores. En la otra interpretación ( diseño fijo ), los regresores X se tratan como constantes conocidas establecidas por un diseño , y y se muestrea condicionalmente en función de los valores de X como en un experimento . Para fines prácticos, esta distinción a menudo no es importante, ya que la estimación y la inferencia se llevan a cabo condicionando X. Todos los resultados indicados en este artículo están dentro del marco de diseño aleatorio.

Modelo de regresión lineal clásico.

El modelo clásico se centra en la estimación e inferencia de "muestra finita", lo que significa que el número de observaciones n es fijo. Esto contrasta con los otros enfoques, que estudian el comportamiento asintótico de MCO y en los que se estudia el comportamiento en un gran número de muestras.

• Especificación correcta . La forma funcional lineal debe coincidir con la forma del proceso real de generación de datos.
• Exogeneidad estricta . Los errores en la regresión deben tener una media condicional cero: ^[16]
  $${\displaystyle \operatorname {E} [\,\varepsilon \mid X\,]=0.}$$
  La consecuencia inmediata del supuesto de exogeneidad es que los errores tienen media cero: E[ ε ] = 0 (para la ley de expectativa total ), y que los regresores no están correlacionados con los errores: E[ X ^T ε ] = 0 .
  El supuesto de exogeneidad es fundamental para la teoría MCO. Si se cumple, las variables regresoras se denominan exógenas . Si no es así, entonces aquellos regresores que están correlacionados con el término de error se denominan endógenos [ ^17] y el estimador MCO se vuelve sesgado. En tal caso se podrá utilizar el método de variables instrumentales para realizar la inferencia.
• Sin dependencia lineal . Todos los regresores en X deben ser linealmente independientes . Matemáticamente, esto significa que la matriz X debe tener el rango de columna completo casi con seguridad: ^[18]
  $${\displaystyle \Pr \!{\big [}\,\operatorname {rank} (X)=p\,{\big ]}=1.}$$
  Generalmente también se supone que los regresores tienen momentos finitos hasta al menos el segundo momento. Entonces la matriz Q _xx = E[ X ^T X  /  n ] es finita y semidefinida positiva.
  Cuando se viola este supuesto, los regresores se denominan linealmente dependientes o perfectamente multicolineales . En tal caso , no se puede conocer el valor del coeficiente de regresión β , aunque todavía es posible predecir los valores de y para nuevos valores de los regresores que se encuentran en el mismo subespacio linealmente dependiente.
• Errores esféricos : ^[18]
  $${\displaystyle \operatorname {Var} [\,\varepsilon \mid X\,]=\sigma ^{2}I_{n},}$$
  donde In _es la matriz identidad en la dimensión n , y σ ² es un parámetro que determina la varianza de cada observación. Este σ ² se considera un parámetro molesto en el modelo, aunque normalmente también se estima. Si se viola este supuesto, las estimaciones de MCO siguen siendo válidas, pero ya no son eficientes.
  Se acostumbra dividir este supuesto en dos partes:
  • Homoscedasticidad : E[  ε _i ²  |  X  ] = σ ² , lo que significa que el término de error tiene la misma varianza σ ² en cada observación. Cuando se viola este requisito se llama heterocedasticidad , en tal caso un estimador más eficiente sería el de mínimos cuadrados ponderados . Si los errores tienen una varianza infinita, entonces las estimaciones de MCO también tendrán una varianza infinita (aunque, según la ley de los grandes números , tenderán hacia los valores verdaderos siempre que los errores tengan una media cero). En este caso,se recomiendan técnicas de estimación robustas .
  • Sin autocorrelación : los errores no están correlacionados entre observaciones: E[  ε _i ε _j  |  X  ] = 0 para yo ≠ j . Este supuesto puede violarse en el contexto de datos de series temporales , datos de panel , muestras de conglomerados, datos jerárquicos, datos de medidas repetidas, datos longitudinales y otros datos con dependencias. En tales casos, los mínimos cuadrados generalizados proporcionan una mejor alternativa que el MCO. Otra expresión de autocorrelación es correlación serial .
• Normalidad . A veces se supone además que los errores tienen una distribución normal condicionada a los regresores: ^[19]
  $${\displaystyle \varepsilon \mid X\sim {\mathcal {N}}(0,\sigma ^{2}I_{n}).}$$
  Esta suposición no es necesaria para la validez del método MCO, aunque se pueden establecer ciertas propiedades adicionales de muestras finitas en caso de que así sea (especialmente en el área de prueba de hipótesis). Además cuando los errores son normales, el estimador MCO es equivalente al estimador de máxima verosimilitud (MLE), y por tanto es asintóticamente eficiente en la clase de todos los estimadores regulares . Es importante destacar que el supuesto de normalidad se aplica sólo a los términos de error; Contrariamente a una idea errónea popular, no es necesario que la variable respuesta (dependiente) tenga una distribución normal. ^[20]

Independiente e idénticamente distribuido (iid)

En algunas aplicaciones, especialmente con datos transversales , se impone una suposición adicional: que todas las observaciones son independientes y están distribuidas de manera idéntica. Esto significa que todas las observaciones se toman de una muestra aleatoria , lo que hace que todos los supuestos enumerados anteriormente sean más simples y fáciles de interpretar. Además, este marco permite establecer resultados asintóticos (como el tamaño de la muestra n  → ∞ ), que se entienden como una posibilidad teórica de obtener nuevas observaciones independientes del proceso de generación de datos . La lista de supuestos en este caso es:

• observaciones iid : ( x _i , y _i ) es independiente y tiene la misma distribución que ( x _j , y _j ) para todo i ≠ j ;
• sin multicolinealidad perfecta : Q _xx = E[  x _i  x _i ^T  ] es una matriz definida positiva ;
• exogeneidad : E[  ε _i  |  x _i  ] = 0;
• homocedasticidad : Var[  ε _i  |  x _yo  ] = σ ² .

Modelo de serie temporal

• El proceso estocástico { xi _, y i _} es estacionario y ergódico ; Si { x _i , y _i } no es estacionario, los resultados de MCO suelen ser espurios a menos que { x _i , y _i } sea cointegrante . ^[21]
• Los regresores están predeterminados : E[ x _i ε _i ] = 0 para todo i = 1, ..., n ;
• La matriz p × p Q _xx = E[  x _i  x _i ^T  ] es de rango completo y, por tanto, definida positiva ;
• { x _i ε _i } es una secuencia en diferencias martingala , con una matriz finita de segundos momentos Q _{xxε ²} = E[  ε _i ² x _i  x _i ^T  ] .

Propiedades de muestras finitas

En primer lugar, bajo el estricto supuesto de exogeneidad, los estimadores MCO y s ² son insesgados , lo que significa que sus valores esperados coinciden con los valores verdaderos de los parámetros: ^{[22] [prueba]} ${\displaystyle \scriptstyle {\hat {\beta }}}$

${\displaystyle \operatorname {E} [\,{\hat {\beta }}\mid X\,]=\beta ,\quad \operatorname {E} [\,s^{2}\mid X\,]=\sigma ^{2}.}$

Si la exogeneidad estricta no se cumple (como es el caso de muchos modelos de series temporales , donde se supone exogeneidad sólo con respecto a los shocks pasados ​​pero no a los futuros), entonces estos estimadores estarán sesgados en muestras finitas.

La matriz de varianza-covarianza (o simplemente matriz de covarianza ) de es igual a ^[23] ${\displaystyle \scriptstyle {\hat {\beta }}}$

${\displaystyle \operatorname {Var} [\,{\hat {\beta }}\mid X\,]=\sigma ^{2}\left(X^{\operatorname {T} }X\right)^{-1}=\sigma ^{2}Q.}$

En particular, el error estándar de cada coeficiente es igual a la raíz cuadrada del j -ésimo elemento diagonal de esta matriz. La estimación de este error estándar se obtiene reemplazando la cantidad desconocida σ ² con su estimación s ² . De este modo, ${\displaystyle \scriptstyle {\hat {\beta }}_{j}}$

${\displaystyle {\widehat {\operatorname {s.\!e.} }}({\hat {\beta }}_{j})={\sqrt {s^{2}\left(X^{\operatorname {T} }X\right)_{jj}^{-1}}}}$

También se puede demostrar fácilmente que el estimador no está correlacionado con los residuos del modelo: ^[23] ${\displaystyle \scriptstyle {\hat {\beta }}}$

${\displaystyle \operatorname {Cov} [\,{\hat {\beta }},{\hat {\varepsilon }}\mid X\,]=0.}$

El teorema de Gauss-Markov establece que bajo el supuesto de errores esféricos (es decir, los errores no deben estar correlacionados y ser homocedásticos ), el estimador es eficiente en la clase de estimadores lineales insesgados. Esto se llama el mejor estimador lineal insesgado (AZUL). La eficiencia debe entenderse como si tuviéramos que encontrar algún otro estimador que fuera lineal en y e insesgado, entonces ^[23] ${\displaystyle \scriptstyle {\hat {\beta }}}$ ${\displaystyle \scriptstyle {\tilde {\beta }}}$

${\displaystyle \operatorname {Var} [\,{\tilde {\beta }}\mid X\,]-\operatorname {Var} [\,{\hat {\beta }}\mid X\,]\geq 0}$

en el sentido de que se trata de una matriz definida no negativa . Este teorema establece la optimización sólo en la clase de estimadores lineales insesgados, lo cual es bastante restrictivo. Dependiendo de la distribución de los términos de error ε , otros estimadores no lineales pueden proporcionar mejores resultados que MCO.

Asumiendo normalidad

Todas las propiedades enumeradas hasta ahora son válidas independientemente de la distribución subyacente de los términos de error. Sin embargo, si está dispuesto a suponer que se cumple el supuesto de normalidad (es decir, que ε ~ N (0, σ ² In ₎ ) , entonces se pueden establecer propiedades adicionales de los estimadores MCO.

El estimador tiene una distribución normal, con media y varianza como se indica anteriormente: ^[24] ${\displaystyle \scriptstyle {\hat {\beta }}}$

${\displaystyle {\hat {\beta }}\ \sim \ {\mathcal {N}}{\big (}\beta ,\ \sigma ^{2}(X^{\mathrm {T} }X)^{-1}{\big )}.}$

Este estimador alcanza el límite de Cramér-Rao para el modelo y, por tanto, es óptimo en la clase de todos los estimadores insesgados. ^[15] Tenga en cuenta que, a diferencia del teorema de Gauss-Markov , este resultado establece la optimización entre estimadores lineales y no lineales, pero sólo en el caso de términos de error normalmente distribuidos.

El estimador s ² será proporcional a la distribución chi-cuadrado : ^[25]

${\displaystyle s^{2}\ \sim \ {\frac {\sigma ^{2}}{n-p}}\cdot \chi _{n-p}^{2}}$

La varianza de este estimador es igual a 2 σ ⁴ /( n  −  p ) , que no alcanza el límite de Cramér-Rao de 2 σ ⁴ / n . Sin embargo se demostró que no existen estimadores insesgados de σ ² con varianza menor que la del estimador s ² . ^[26] Si estamos dispuestos a permitir estimadores sesgados y consideramos la clase de estimadores que son proporcionales a la suma de residuos cuadrados (SSR) del modelo, entonces el mejor estimador (en el sentido del error cuadrático medio ) en este La clase será ^~ σ ² = SSR  /  ( n  −  p  + 2 ) , que incluso supera el límite de Cramér-Rao en el caso de que solo haya un regresor ( p = 1 ). ^[27]

Además, los estimadores y s ² son independientes , ^[28] hecho que resulta útil a la hora de construir las pruebas t y F para la regresión. ${\displaystyle \scriptstyle {\hat {\beta }}}$

Observaciones influyentes

Como se mencionó anteriormente, el estimador es lineal en y , lo que significa que representa una combinación lineal de las variables dependientes y _i . Los pesos en esta combinación lineal son funciones de los regresores X y generalmente son desiguales. Las observaciones con ponderaciones altas se denominan influyentes porque tienen un efecto más pronunciado sobre el valor del estimador. ${\displaystyle {\hat {\beta }}}$

Para analizar qué observaciones son influyentes, eliminamos una j -ésima observación específica y consideramos cuánto van a cambiar las cantidades estimadas (de manera similar al método jackknife ). Se puede demostrar que el cambio en el estimador MCO para β será igual a ^[29]

${\displaystyle {\hat {\beta }}^{(j)}-{\hat {\beta }}=-{\frac {1}{1-h_{j}}}(X^{\mathrm {T} }X)^{-1}x_{j}^{\mathrm {T} }{\hat {\varepsilon }}_{j}\,,}$

donde h _j = x _j ^T  ( X ^T X ) ⁻¹ x _j es el j -ésimo elemento diagonal de la matriz hat P , y x _j es el vector de regresores correspondientes a la j -ésima observación. De manera similar, el cambio en el valor previsto para la j -ésima observación resultante de omitir esa observación del conjunto de datos será igual a ^[29]

${\displaystyle {\hat {y}}_{j}^{(j)}-{\hat {y}}_{j}=x_{j}^{\mathrm {T} }{\hat {\beta }}^{(j)}-x_{j}^{\operatorname {T} }{\hat {\beta }}=-{\frac {h_{j}}{1-h_{j}}}\,{\hat {\varepsilon }}_{j}}$

De las propiedades de la matriz hat, 0 ≤ h _j ≤ 1 , y suman p , de modo que en promedio h _j ≈ p/n . Estas cantidades h _j se denominan apalancamientos y las observaciones con h _j elevado se denominan puntos de apalancamiento . ^[30] Por lo general, las observaciones con un alto apalancamiento deberían examinarse más cuidadosamente, en caso de que sean erróneas, o atípicas, o de alguna otra manera atípicas del resto del conjunto de datos.

Regresión particionada

A veces, las variables y los parámetros correspondientes en la regresión se pueden dividir lógicamente en dos grupos, de modo que la regresión tome forma.

${\displaystyle y=X_{1}\beta _{1}+X_{2}\beta _{2}+\varepsilon ,}$

donde X ₁ y X ₂ tienen dimensiones n × p ₁ , n × p ₂ y β ₁ , β ₂ son vectores p ₁ × 1 y p ₂ × 1 , con p ₁ + p ₂ = p .

El teorema de Frisch-Waugh-Lovell establece que en esta regresión los residuos y la estimación de MCO serán numéricamente idénticos a los residuos y la estimación de MCO para β ₂ en la siguiente regresión: ^[31] ${\displaystyle {\hat {\varepsilon }}}$ ${\displaystyle \scriptstyle {\hat {\beta }}_{2}}$

${\displaystyle M_{1}y=M_{1}X_{2}\beta _{2}+\eta \,,}$

donde M ₁ es la matriz aniquiladora para los regresores X ₁ .

El teorema se puede utilizar para establecer una serie de resultados teóricos. Por ejemplo, tener una regresión con una constante y otro regresor equivale a restar las medias de la variable dependiente y el regresor y luego ejecutar la regresión para las variables desmediadas pero sin el término constante.

Estimación restringida

Supongamos que se sabe que los coeficientes de la regresión satisfacen un sistema de ecuaciones lineales

${\displaystyle A\colon \quad Q^{\operatorname {T} }\beta =c,\,}$

donde Q es una matriz p × q de rango completo, y c es un vector q ×1 de constantes conocidas, donde q < p . En este caso la estimación de mínimos cuadrados equivale a minimizar la suma de los residuos cuadrados del modelo sujeto a la restricción A. El estimador de mínimos cuadrados restringidos (CLS) puede obtenerse mediante una fórmula explícita: ^[32]

${\displaystyle {\hat {\beta }}^{c}={\hat {\beta }}-(X^{\operatorname {T} }X)^{-1}Q{\Big (}Q^{\operatorname {T} }(X^{\operatorname {T} }X)^{-1}Q{\Big )}^{-1}(Q^{\operatorname {T} }{\hat {\beta }}-c).}$

Esta expresión para el estimador restringido es válida siempre que la matriz X ^T X sea invertible. Desde el principio de este artículo se supuso que esta matriz es de rango completo y se observó que cuando la condición de rango falla, β no será identificable. Sin embargo, puede suceder que al agregar la restricción A se haga identificable a β , en cuyo caso nos gustaría encontrar la fórmula para el estimador. El estimador es igual a ^[33]

${\displaystyle {\hat {\beta }}^{c}=R(R^{\operatorname {T} }X^{\operatorname {T} }XR)^{-1}R^{\operatorname {T} }X^{\operatorname {T} }y+{\Big (}I_{p}-R(R^{\operatorname {T} }X^{\operatorname {T} }XR)^{-1}R^{\operatorname {T} }X^{\operatorname {T} }X{\Big )}Q(Q^{\operatorname {T} }Q)^{-1}c,}$

donde R es una matriz p ×( p  −  q ) tal que la matriz [ QR ] no es singular y R ^T Q = 0 . Una matriz de este tipo siempre se puede encontrar, aunque generalmente no es única. La segunda fórmula coincide con la primera en el caso de que X ^T X sea invertible. ^[33]

Propiedades de muestra grandes

Los estimadores de mínimos cuadrados son estimaciones puntuales de los parámetros β del modelo de regresión lineal . Sin embargo, en general también queremos saber qué tan cerca podrían estar esas estimaciones de los valores reales de los parámetros. En otras palabras, queremos construir las estimaciones de intervalo .

Como no hemos hecho ninguna suposición sobre la distribución del término de error ε _i , es imposible inferir la distribución de los estimadores y . Sin embargo, podemos aplicar el teorema del límite central para derivar sus propiedades asintóticas cuando el tamaño de muestra n tiende a infinito. Si bien el tamaño de la muestra es necesariamente finito, se acostumbra suponer que n es "lo suficientemente grande" como para que la verdadera distribución del estimador MCO esté cerca de su límite asintótico. ${\displaystyle {\hat {\beta }}}$ ${\displaystyle {\hat {\sigma }}^{2}}$

Podemos demostrar que bajo los supuestos del modelo, el estimador de mínimos cuadrados para β es consistente (es decir, converge en probabilidad a β ) y asintóticamente normal: ^[prueba] ${\displaystyle {\hat {\beta }}}$

${\displaystyle ({\hat {\beta }}-\beta )\ {\xrightarrow {d}}\ {\mathcal {N}}{\big (}0,\;\sigma ^{2}Q_{xx}^{-1}{\big )},}$

dónde ${\displaystyle Q_{xx}=X^{\operatorname {T} }X.}$

Intervalos

Utilizando esta distribución asintótica, se pueden construir intervalos de confianza bilaterales aproximados para el j -ésimo componente del vector como ${\displaystyle {\hat {\beta }}}$

${\displaystyle \beta _{j}\in {\bigg [}\ {\hat {\beta }}_{j}\pm q_{1-{\frac {\alpha }{2}}}^{{\mathcal {N}}(0,1)}\!{\sqrt {{\hat {\sigma }}^{2}\left[Q_{xx}^{-1}\right]_{jj}}}\ {\bigg ]}}$   en el nivel de confianza 1 −  α ,

donde q denota la función cuantil de la distribución normal estándar, y [·] _jj es el j -ésimo elemento diagonal de una matriz.

De manera similar, el estimador de mínimos cuadrados para σ ² también es consistente y asintóticamente normal (siempre que exista el cuarto momento de ε _i ) con distribución limitante

${\displaystyle ({\hat {\sigma }}^{2}-\sigma ^{2})\ {\xrightarrow {d}}\ {\mathcal {N}}\left(0,\;\operatorname {E} \left[\varepsilon _{i}^{4}\right]-\sigma ^{4}\right).}$

Estas distribuciones asintóticas se pueden utilizar para predicción, probar hipótesis, construir otros estimadores, etc. Consideremos como ejemplo el problema de la predicción. Supongamos que hay algún punto dentro del dominio de distribución de los regresores y se quiere saber cuál habría sido la variable de respuesta en ese punto. La respuesta media es la cantidad , mientras que la respuesta prevista es . Claramente la respuesta predicha es una variable aleatoria, su distribución se puede derivar de la de : ${\displaystyle x_{0}}$ ${\displaystyle y_{0}=x_{0}^{\mathrm {T} }\beta }$ ${\displaystyle {\hat {y}}_{0}=x_{0}^{\mathrm {T} }{\hat {\beta }}}$ ${\displaystyle {\hat {\beta }}}$

${\displaystyle \left({\hat {y}}_{0}-y_{0}\right)\ {\xrightarrow {d}}\ {\mathcal {N}}\left(0,\;\sigma ^{2}x_{0}^{\mathrm {T} }Q_{xx}^{-1}x_{0}\right),}$

lo que permite construir intervalos de confianza para la respuesta media : ${\displaystyle y_{0}}$

${\displaystyle y_{0}\in \left[\ x_{0}^{\mathrm {T} }{\hat {\beta }}\pm q_{1-{\frac {\alpha }{2}}}^{{\mathcal {N}}(0,1)}\!{\sqrt {{\hat {\sigma }}^{2}x_{0}^{\mathrm {T} }Q_{xx}^{-1}x_{0}}}\ \right]}$   en el nivel de confianza 1 −  α .

Evaluación de la hipótesis

Se utilizan especialmente dos pruebas de hipótesis. Primero, uno quiere saber si la ecuación de regresión estimada es mejor que simplemente predecir que todos los valores de la variable de respuesta son iguales a su media muestral (si no, se dice que no tiene poder explicativo). La hipótesis nula de que la regresión estimada no tiene valor explicativo se prueba mediante una prueba F. Si se encuentra que el valor F calculado es lo suficientemente grande como para exceder su valor crítico para el nivel de significancia elegido previamente, se rechaza la hipótesis nula y se acepta la hipótesis alternativa de que la regresión tiene poder explicativo. En caso contrario, se acepta la hipótesis nula de falta de poder explicativo.

En segundo lugar, para cada variable explicativa de interés, se quiere saber si su coeficiente estimado difiere significativamente de cero, es decir, si esta variable explicativa particular de hecho tiene poder explicativo para predecir la variable de respuesta. Aquí la hipótesis nula es que el coeficiente verdadero es cero. Esta hipótesis se prueba calculando el estadístico t del coeficiente , como la relación entre la estimación del coeficiente y su error estándar . Si el estadístico t es mayor que un valor predeterminado, se rechaza la hipótesis nula y se encuentra que la variable tiene poder explicativo, con su coeficiente significativamente diferente de cero. En caso contrario, se acepta la hipótesis nula de un valor cero del coeficiente verdadero.

Además, la prueba de Chow se utiliza para comprobar si dos submuestras tienen los mismos valores de coeficientes verdaderos subyacentes. La suma de los residuos cuadrados de las regresiones en cada uno de los subconjuntos y en el conjunto de datos combinado se compara calculando un estadístico F; si éste excede un valor crítico, se rechaza la hipótesis nula de que no hay diferencia entre los dos subconjuntos; en caso contrario, se acepta.

Ejemplo con datos reales

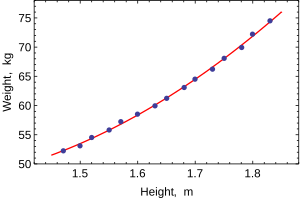
El siguiente conjunto de datos proporciona alturas y pesos promedio para mujeres estadounidenses de entre 30 y 39 años (fuente: The World Almanac and Book of Facts, 1975 ).

Cuando solo se modela una variable dependiente, un diagrama de dispersión sugerirá la forma y la fuerza de la relación entre la variable dependiente y los regresores. También podría revelar valores atípicos, heterocedasticidad y otros aspectos de los datos que pueden complicar la interpretación de un modelo de regresión ajustado. El diagrama de dispersión sugiere que la relación es fuerte y puede aproximarse como una función cuadrática. OLS puede manejar relaciones no lineales introduciendo el regresor HEIGHT ² . El modelo de regresión se convierte entonces en un modelo lineal múltiple:

${\displaystyle w_{i}=\beta _{1}+\beta _{2}h_{i}+\beta _{3}h_{i}^{2}+\varepsilon _{i}.}$

Regresión ajustada

El resultado de los paquetes estadísticos más populares será similar a este:

En esta tabla:

• La columna Valor proporciona las estimaciones de mínimos cuadrados de los parámetros β _j
• La columna de error estándar muestra los errores estándar de cada estimación de coeficiente: ${\displaystyle {\hat {\sigma }}_{j}=\left({\hat {\sigma }}^{2}\left[Q_{xx}^{-1}\right]_{jj}\right)^{\frac {1}{2}}}$
• Las columnas del estadístico t y del valor p prueban si alguno de los coeficientes podría ser igual a cero. El estadístico t se calcula simplemente como . Si los errores ε siguen una distribución normal, t sigue una distribución t de Student. En condiciones más débiles, t es asintóticamente normal. Valores grandes de t indican que la hipótesis nula puede rechazarse y que el coeficiente correspondiente no es cero. La segunda columna, valor p , expresa los resultados de la prueba de hipótesis como un nivel de significancia . Convencionalmente, los valores de p inferiores a 0,05 se toman como prueba de que el coeficiente poblacional es distinto de cero. ${\displaystyle t={\hat {\beta }}_{j}/{\hat {\sigma }}_{j}}$
• R cuadrado es el coeficiente de determinación que indica la bondad de ajuste de la regresión. Este estadístico será igual a uno si el ajuste es perfecto y cero cuando los regresores X no tengan poder explicativo alguno. Esta es una estimación sesgada del R cuadrado de la población y nunca disminuirá si se agregan regresores adicionales, incluso si son irrelevantes.
• El R cuadrado ajustado es una versión ligeramente modificada de , diseñada para penalizar el número excesivo de regresores que no aumentan el poder explicativo de la regresión. Esta estadística siempre es menor que , puede disminuir a medida que se agregan nuevos regresores e incluso ser negativa para modelos que no se ajustan bien: ${\displaystyle R^{2}}$ ${\displaystyle R^{2}}$

${\displaystyle {\overline {R}}^{2}=1-{\frac {n-1}{n-p}}(1-R^{2})}$

• La probabilidad logarítmica se calcula bajo el supuesto de que los errores siguen una distribución normal. Aunque la suposición no es muy razonable, esta estadística aún puede resultar útil al realizar pruebas de LR.
• La estadística de Durbin-Watson prueba si existe alguna evidencia de correlación serial entre los residuos. Como regla general, un valor menor que 2 será una evidencia de correlación positiva.
• El criterio de información de Akaike y el criterio de Schwarz se utilizan para la selección del modelo. Generalmente, al comparar dos modelos alternativos, valores más pequeños de uno de estos criterios indicarán un mejor modelo. ^[34]
• El error estándar de regresión es una estimación de σ , error estándar del término de error.
• La suma total de cuadrados , la suma de cuadrados del modelo y la suma de cuadrados residual nos indican qué parte de la variación inicial en la muestra fue explicada por la regresión.
• El estadístico F intenta probar la hipótesis de que todos los coeficientes (excepto el intercepto) son iguales a cero. Esta estadística tiene una distribución F ( p–1 , n–p ) bajo la hipótesis nula y el supuesto de normalidad, y su valor p indica la probabilidad de que la hipótesis sea verdadera. Tenga en cuenta que cuando los errores no son normales, esta estadística deja de ser válida y se deben utilizar otras pruebas como la prueba de Wald o la prueba LR .

Parcela de residuos

El análisis de mínimos cuadrados ordinario a menudo incluye el uso de gráficos de diagnóstico diseñados para detectar desviaciones de los datos de la forma supuesta del modelo. Estas son algunas de las gráficas de diagnóstico comunes:

• Residuos frente a las variables explicativas del modelo. Una relación no lineal entre estas variables sugiere que la linealidad de la función media condicional puede no cumplirse. Diferentes niveles de variabilidad en los residuos para diferentes niveles de variables explicativas sugieren una posible heterocedasticidad.
• Residuos frente a variables explicativas que no están en el modelo. Cualquier relación de los residuos con estas variables sugeriría considerar estas variables para su inclusión en el modelo.
• Residuos frente a los valores ajustados, . ${\displaystyle {\hat {y}}}$
• Residuos contra el residual anterior. Este gráfico puede identificar correlaciones seriales en los residuos.

Una consideración importante al realizar inferencias estadísticas utilizando modelos de regresión es cómo se muestrearon los datos. En este ejemplo, los datos son promedios en lugar de mediciones de mujeres individuales. El ajuste del modelo es muy bueno, pero esto no implica que el peso de una mujer individual pueda predecirse con gran precisión basándose únicamente en su altura.

Sensibilidad al redondeo

Este ejemplo también demuestra que los coeficientes determinados por estos cálculos son sensibles a cómo se preparan los datos. Las alturas se redondearon originalmente a la pulgada más cercana y se convirtieron y redondearon al centímetro más cercano. Dado que el factor de conversión es de una pulgada a 2,54 cm, esta no es una conversión exacta. Las pulgadas originales se pueden recuperar mediante Round(x/0.0254) y luego volver a convertirlas al sistema métrico sin redondear. Si se hace esto los resultados serán:

Residuos de un ajuste cuadrático para datos convertidos correcta e incorrectamente.

El uso de cualquiera de estas ecuaciones para predecir el peso de una mujer de 5' 6" (1,6764 m) da valores similares: 62,94 kg con redondeo versus 62,98 kg sin redondeo. Por lo tanto, una variación aparentemente pequeña en los datos tiene un efecto real en los coeficientes. pero un pequeño efecto sobre los resultados de la ecuación.

Si bien esto puede parecer inocuo en el medio del rango de datos, podría volverse significativo en los extremos o en el caso en que el modelo ajustado se utilice para proyectar fuera del rango de datos ( extrapolación ).

Esto resalta un error común: este ejemplo es un abuso de MCO que inherentemente requiere que los errores en la variable independiente (en este caso, altura) sean cero o al menos insignificantes. El redondeo inicial a la pulgada más cercana más cualquier error de medición real constituye un error finito y no despreciable. Como resultado, los parámetros ajustados no son las mejores estimaciones que se supone que son. Aunque no es totalmente espurio , el error en la estimación dependerá del tamaño relativo de los errores xey .

Otro ejemplo con datos menos reales

Planteamiento del problema

Podemos utilizar el mecanismo de mínimos cuadrados para calcular la ecuación de una órbita de dos cuerpos en coordenadas de base polar. La ecuación que normalmente se utiliza es ¿ dónde está el radio de la distancia a la que se encuentra el objeto de uno de los cuerpos? En la ecuación, los parámetros y se utilizan para determinar la trayectoria de la órbita. Hemos medido los siguientes datos. ${\displaystyle r(\theta )={\frac {p}{1-e\cos(\theta )}}}$ ${\displaystyle r(\theta )}$ ${\displaystyle p}$ ${\displaystyle e}$

Necesitamos encontrar la aproximación de mínimos cuadrados de y para los datos dados. ${\displaystyle e}$ ${\displaystyle p}$

Solución

Primero necesitamos representar e y p en forma lineal. Entonces vamos a reescribir la ecuación como . Además, se podrían ajustar los ápsides expandiendo con un parámetro adicional como , que es lineal en ambos y en la función de base adicional , utilizada para extra . Usamos la forma original de dos parámetros para representar nuestros datos de observación como: ${\displaystyle r(\theta )}$ ${\displaystyle {\frac {1}{r(\theta )}}={\frac {1}{p}}-{\frac {e}{p}}\cos(\theta )}$ ${\displaystyle \cos(\theta )}$ ${\displaystyle \cos(\theta -\theta _{0})=\cos(\theta )\cos(\theta _{0})+\sin(\theta )\sin(\theta _{0})}$ ${\displaystyle \cos(\theta )}$ ${\displaystyle \sin(\theta )}$ ${\displaystyle \tan \theta _{0}=\sin(\theta _{0})/\cos(\theta _{0})}$

${\displaystyle A^{T}A{\binom {x}{y}}=A^{T}b}$donde es y es y se construye siendo la primera columna el coeficiente de y la segunda columna el coeficiente de y son los valores para los respectivos so y ${\displaystyle x}$ ${\displaystyle {\frac {1}{p}}}$ ${\displaystyle y}$ ${\displaystyle {\frac {e}{p}}}$ ${\displaystyle A}$ ${\displaystyle {\frac {1}{p}}}$ ${\displaystyle {\frac {e}{p}}}$ ${\displaystyle b}$ ${\displaystyle {\frac {1}{r(\theta )}}}$ ${\displaystyle A={\begin{bmatrix}1&-0.731354\\1&-0.707107\\1&-0.615661\\1&\ 0.052336\\1&0.309017\\1&0.438371\end{bmatrix}}}$ ${\displaystyle b={\begin{bmatrix}0.21220\\0.21958\\0.24741\\0.45071\\0.52883\\0.56820\end{bmatrix}}.}$

Al resolver obtenemos ${\displaystyle {\binom {x}{y}}={\binom {0.43478}{0.30435}}}$

y entonces ${\displaystyle p={\frac {1}{x}}=2.3000}$ ${\displaystyle e=p\cdot y=0.70001}$

Ver también

• Mínimos cuadrados bayesianos
• Regresión de Fama-MacBeth
• Mínimos cuadrados no lineales
• Métodos numéricos para mínimos cuadrados lineales.
• Identificación de sistemas no lineales.

Referencias

1. "¿Cuál es una lista completa de los supuestos habituales para la regresión lineal?". Validación cruzada . Consultado el 28 de septiembre de 2022 .
2. Goldberger, Arthur S. (1964). "Regresión lineal clásica". Teoría econométrica. Nueva York: John Wiley & Sons. págs.158. ISBN 0-471-31101-4.
3. Hayashi, Fumio (2000). Econometría . Prensa de la Universidad de Princeton. pag. 15.
4. Hayashi (2000, página 18)
5. Ghilani, Charles D.; Pablo r. Wolf, Ph. D. (12 de junio de 2006). Cálculos de ajuste: análisis de datos espaciales. ISBN 9780471697282.
6. Hofmann-Wellenhof, Bernhard; Lichtenegger, Herbert; Wasle, Elmar (20 de noviembre de 2007). GNSS – Sistemas globales de navegación por satélite: GPS, GLONASS, Galileo y más. ISBN 9783211730171.
7. Xu, Guochang (5 de octubre de 2007). GPS: Teoría, Algoritmos y Aplicaciones. ISBN 9783540727156.
8. Hayashi (2000, página 19)
9. Julian Faraway (2000), Regresión práctica y Anova usando R
10. Kenney, J.; Manteniendo, ES (1963). Matemáticas de la Estadística . van Nostrand. pag. 187.
11. Zwillinger, D. (1995). Tablas y fórmulas matemáticas estándar . Chapman y Hall/CRC. pag. 626.ISBN​ 0-8493-2479-3.
12. Hayashi (2000, página 20)
13. Akbarzadeh, Vahab (7 de mayo de 2014). "Estimación de líneas".
14. Hayashi (2000, página 49)
15. Hayashi (2000, página 52)
16. Hayashi (2000, página 7)
17. Hayashi (2000, página 187)
18. Hayashi (2000, página 10)
19. Hayashi (2000, página 34)
20. Williams, MN; Grajales, CA G; Kurkiewicz, D (2013). "Supuestos de regresión múltiple: corregir dos conceptos erróneos". Evaluación práctica, investigación y evaluación . 18 (11).
21. "Recuerdo sobre la salida de EViews" (PDF) . Consultado el 28 de diciembre de 2020 .
22. Hayashi (2000, páginas 27, 30)
23. Hayashi (2000, página 27)
24. Amemiya, Takeshi (1985). Econometría avanzada . Prensa de la Universidad de Harvard. pag. 13.ISBN​ 9780674005600.
25. Amemiya (1985, página 14)
26. Rao, CR (1973). Inferencia estadística lineal y sus aplicaciones (Segunda ed.). Nueva York: J. Wiley & Sons. pag. 319.ISBN​ 0-471-70823-2.
27. Amemiya (1985, página 20)
28. Amemiya (1985, página 27)
29. Davidson, Russell; MacKinnon, James G. (1993). Estimación e Inferencia en Econometría . Nueva York: Oxford University Press. pag. 33.ISBN​ 0-19-506011-3.
30. Davidson y MacKinnon (1993, página 36)
31. Davidson y MacKinnon (1993, página 20)
32. Amemiya (1985, página 21)
33. Amemiya (1985, página 22)
34. Burnham, Kenneth P.; David Anderson (2002). Selección de modelos e inferencia multimodelo (2ª ed.). Saltador. ISBN 0-387-95364-7.

Otras lecturas

• Dougherty, Christopher (2002). Introducción a la econometría (2ª ed.). Nueva York: Oxford University Press. págs. 48-113. ISBN 0-19-877643-8.
• Gujarati, Damodar N .; Portero, amanecer C. (2009). Economía Básica (Quinta ed.). Boston: McGraw-Hill Irwin. págs. 55–96. ISBN 978-0-07-337577-9.
• Heij, Christian; Bóer, Paul; Fransés, Philip H.; Kloek, Teun; van Dijk, Herman K. (2004). Métodos econométricos con aplicaciones en economía y negocios (1ª ed.). Oxford: Prensa de la Universidad de Oxford. págs. 76-115. ISBN 978-0-19-926801-6.
• Colina, R. Carter; Griffiths, William E.; Lim, Guay C. (2008). Principios de econometría (3ª ed.). Hoboken, Nueva Jersey: John Wiley & Sons. págs. 8–47. ISBN 978-0-471-72360-8.
• Wooldridge, Jeffrey (2008). "El modelo de regresión simple". Introducción a la econometría: un enfoque moderno (4ª ed.). Mason, OH: Aprendizaje Cengage. págs. 22–67. ISBN 978-0-324-58162-1.