grupo prufer

El grupo Prüfer 2 con presentación ⟨ g _n : g _{n +1} ² = g _n , g ₁ ² = e ⟩ , ilustrado como un subgrupo del círculo unitario en el plano complejo

En matemáticas, específicamente en teoría de grupos , el p -grupo de Prüfer o el p -grupo cuasicíclico o p ^∞ -grupo, Z ( p ^∞ ), para un número primo p es el único p -grupo en el que cada elemento tiene p diferente p -ésimas raíces.

Los p -grupos de Prüfer son grupos abelianos contables que son importantes en la clasificación de infinitos grupos abelianos: ellos (junto con el grupo de números racionales ) forman los componentes básicos más pequeños de todos los grupos divisibles .

Los grupos llevan el nombre de Heinz Prüfer , un matemático alemán de principios del siglo XX.

Construcciones de Z ( p ∞ )

El grupo p de Prüfer se puede identificar con el subgrupo del grupo circular , U(1), que consta de todas las p ⁿ -ésimas raíces de la unidad como n abarca todos los números enteros no negativos:

${\displaystyle \mathbf {Z} (p^{\infty })=\{\exp(2\pi im/p^{n})\mid 0\leq m<p^{n},\,n\in \mathbf {Z} ^{+}\}=\{z\in \mathbf {C} \mid z^{(p^{n})}=1{\text{ for some }}n\in \mathbf {Z} ^{+}\}.\;}$

La operación de grupo aquí es la multiplicación de números complejos .

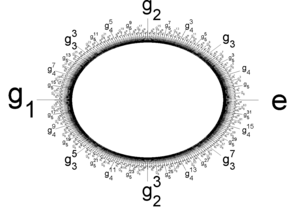
hay una presentacion

${\displaystyle \mathbf {Z} (p^{\infty })=\langle \,g_{1},g_{2},g_{3},\ldots \mid g_{1}^{p}=1,g_{2}^{p}=g_{1},g_{3}^{p}=g_{2},\dots \,\rangle .}$

Aquí, la operación de grupo en Z ( p ^∞ ) se escribe como multiplicación.

Alternativa y equivalente, el grupo p de Prüfer puede definirse como el subgrupo p de Sylow del grupo cociente Q / Z , que consta de aquellos elementos cuyo orden es una potencia de p :

${\displaystyle \mathbf {Z} (p^{\infty })=\mathbf {Z} [1/p]/\mathbf {Z} }$

(donde Z [1/ p ] denota el grupo de todos los números racionales cuyo denominador es una potencia de p , utilizando la suma de números racionales como operación de grupo).

Para cada número natural n , considere el grupo cociente Z / p ⁿ Z y la incrustación Z / p ⁿ Z → Z / p ^{n +1} Z inducida por la multiplicación por p . El límite directo de este sistema es Z ( p ^∞ ):

${\displaystyle \mathbf {Z} (p^{\infty })=\varinjlim \mathbf {Z} /p^{n}\mathbf {Z} .}$

Si realizamos el límite directo en la categoría de grupos topológicos, entonces debemos imponer una topología a cada uno de ellos y tomar la topología final de . Si deseamos ser Hausdorff , debemos imponer la topología discreta en cada uno de los , lo que resulta en tener la topología discreta. ${\displaystyle \mathbf {Z} /p^{n}\mathbf {Z} }$ ${\displaystyle \mathbf {Z} (p^{\infty })}$ ${\displaystyle \mathbf {Z} (p^{\infty })}$ ${\displaystyle \mathbf {Z} /p^{n}\mathbf {Z} }$ ${\displaystyle \mathbf {Z} (p^{\infty })}$

También podemos escribir

${\displaystyle \mathbf {Z} (p^{\infty })=\mathbf {Q} _{p}/\mathbf {Z} _{p}}$

donde Q _p denota el grupo aditivo de p -números ádicos y Z _p es el subgrupo de p -números enteros ádicos.

Propiedades

La lista completa de subgrupos del grupo p de Prüfer Z ( p ^∞ ) = Z [1/ p ]/ Z es:

${\displaystyle 0\subsetneq \left({1 \over p}\mathbf {Z} \right)/\mathbf {Z} \subsetneq \left({1 \over p^{2}}\mathbf {Z} \right)/\mathbf {Z} \subsetneq \left({1 \over p^{3}}\mathbf {Z} \right)/\mathbf {Z} \subsetneq \cdots \subsetneq \mathbf {Z} (p^{\infty })}$

Aquí, cada uno es un subgrupo cíclico de Z ( p ^∞ ) con p ⁿ elementos; contiene precisamente aquellos elementos de Z ( p ^∞ ) cuyo orden divide a p ⁿ y corresponde al conjunto de p ⁿ -ésimas raíces de la unidad. ${\displaystyle \left({1 \over p^{n}}\mathbf {Z} \right)/\mathbf {Z} }$

Los p -grupos de Prüfer son los únicos grupos infinitos cuyos subgrupos están totalmente ordenados por inclusión. Esta secuencia de inclusiones expresa el grupo p de Prüfer como el límite directo de sus subgrupos finitos. Como no existe un subgrupo máximo de un p -grupo de Prüfer, es su propio subgrupo de Frattini .

Dada esta lista de subgrupos, está claro que los p -grupos de Prüfer son indescomponibles (no se pueden escribir como una suma directa de subgrupos propios). Más es cierto: los grupos p de Prüfer son subdirectamente irreducibles . Un grupo abeliano es subdirectamente irreducible si y sólo si es isomorfo a un grupo p cíclico finito o a un grupo de Prüfer.

El grupo p de Prüfer es el único grupo p infinito que es localmente cíclico (cada conjunto finito de elementos genera un grupo cíclico). Como se vio arriba, todos los subgrupos propios de Z ( p ^∞ ) son finitos. Los p -grupos de Prüfer son los únicos grupos abelianos infinitos con esta propiedad. ^[1]

Los grupos p de Prüfer son divisibles . Desempeñan un papel importante en la clasificación de grupos divisibles; junto con los números racionales son los grupos divisibles más simples. Más precisamente: un grupo abeliano es divisible si y sólo si es la suma directa de un número (posiblemente infinito) de copias de Q y un número (posiblemente infinito) de copias de Z ( p ^∞ ) para cada primo p . Los números ( cardinales ) de copias de Q y Z ( p ^∞ ) que se utilizan en esta suma directa determinan el grupo divisible hasta el isomorfismo. ^[2]

Como grupo abeliano (es decir, como módulo Z ), Z ( p ^∞ ) es artiniano pero no noetheriano . ^[3] Por lo tanto, puede usarse como un contraejemplo contra la idea de que cada módulo artiniano es noetheriano (mientras que cada anillo artiniano es noetheriano).

El anillo de endomorfismo de Z ( p ^∞ ) es isomorfo al anillo de p -enteros ádicos Z _p . ^[4]

En la teoría de grupos topológicos localmente compactos, el grupo p de Prüfer (dotado de la topología discreta ) es el dual de Pontryagin del grupo compacto de enteros p -ádicos , y el grupo de enteros p -ádicos es el dual de Pontryagin del p de Prüfer -grupo. ^[5]

Ver también

• p -enteros ádicos , que se pueden definir como el límite inverso de los subgrupos finitos del grupo p de Prüfer .
• Números racionales diádicos , racionales de la forma a /2 ^b . El grupo Prüfer 2 puede verse como los racionales diádicos módulo 1.
• Grupo cíclico ( análogo finito )
• Grupo circular ( análogo incontablemente infinito )

Notas

1. Ver Vil'yams (2001)
2. Véase Kaplansky (1965)
3. Véase también Jacobson (2009), pág. 102, ej. 2.
4. Ver Vil'yams (2001)
5. DL Armacost y WL Armacost, "Sobre grupos p-téticos", Pacific J. Math. , 41 , núm. 2 (1972), 295–301

Referencias

• Jacobson, Nathan (2009). Álgebra básica . vol. 2 (2ª ed.). Dover. ISBN 978-0-486-47187-7.
• Pierre Antoine Grillet (2007). Álgebra abstracta . Saltador. ISBN 978-0-387-71567-4.
• Kaplansky, Irving (1965). Infinitos Grupos Abelianos . Prensa de la Universidad de Michigan.
• NN Vil'yams (2001) [1994], "Grupo cuasi cíclico", Enciclopedia de Matemáticas , EMS Press