Algoritmo de multiplicación

Algoritmo para multiplicar dos números

Un algoritmo de multiplicación es un algoritmo (o método) para multiplicar dos números. Dependiendo del tamaño de los números, diferentes algoritmos son más eficientes que otros. Desde la llegada del sistema numérico decimal han existido algoritmos de multiplicación eficientes .

multiplicación larga

Si se utiliza un sistema de numeración posicional , en las escuelas se enseña una forma natural de multiplicar números como multiplicación larga , a veces llamada multiplicación de la escuela primaria , a veces llamada algoritmo estándar : multiplicar el multiplicando por cada dígito del multiplicador y luego sumar todos los resultados correctamente desplazados. Requiere memorización de la tabla de multiplicar de un solo dígito.

Este es el algoritmo habitual para multiplicar números más grandes a mano en base 10. Una persona que realiza una multiplicación larga en papel anotará todos los productos y luego los sumará; un usuario de ábaco sumará los productos tan pronto como se calcule cada uno.

Ejemplo

Este ejemplo utiliza una multiplicación larga para multiplicar 23.958.233 (multiplicando) por 5.830 (multiplicador) y llega a 139.676.498.390 para el resultado (producto).

 23958233× 5830——————————————— 00000000 ( = 23.958.233 × 0) 71874699 ( = 23.958.233 × 30) 191665864 ( = 23.958.233 × 800)+ 119791165 ( = 23.958.233 × 5.000)——————————————— 139676498390 ( = 139.676.498.390)

Otras notaciones

En algunos países como Alemania , la multiplicación anterior se representa de manera similar pero con el producto original mantenido en posición horizontal y el cálculo comienza con el primer dígito del multiplicador: ^[1]

23958233 · 5830——————————————— 119791165 191665864 71874699 00000000——————————————— 139676498390

El siguiente pseudocódigo describe el proceso de multiplicación anterior. Mantiene solo una fila para mantener la suma que finalmente se convierte en el resultado. Tenga en cuenta que el operador '+=' se utiliza para indicar la suma del valor existente y la operación de almacenamiento (similar a lenguajes como Java y C) para que sea más compacto.

multiplicar ( a [ 1 .. p ] , b [ 1 .. q ] , base ) // Operandos que contienen los dígitos más a la derecha en el índice 1    producto = [ 1 .. p + q ] // Asignar espacio para el resultado    para b_i = 1 a q // para todos los dígitos en b       llevar = 0   for a_i = 1 to p // para todos los dígitos en a       producto [ a_i + b_i - 1 ] += llevar + a [ a_i ] * b [ b_i ]           llevar = producto [ a_i + b_i - 1 ] / base         producto [ a_i + b_i - 1 ] = producto [ a_i + b_i - 1 ] mod base             producto [ b_i + p ] = acarreo // el último dígito proviene del acarreo final      devolver producto 

Uso en computadoras

Algunos chips implementan una multiplicación larga, en hardware o en microcódigo , para varios tamaños de palabras enteras y de punto flotante. En aritmética de precisión arbitraria , es común utilizar multiplicaciones largas con la base establecida en 2 ^w , donde w es el número de bits de una palabra, para multiplicar números relativamente pequeños. Para multiplicar dos números con n dígitos usando este método, se necesitan alrededor de n ² operaciones. Más formalmente, multiplicar dos números de n dígitos mediante una multiplicación larga requiere Θ ( n ² ) operaciones de un solo dígito (sumas y multiplicaciones).

Cuando se implementan en software, los algoritmos de multiplicación largos deben lidiar con el desbordamiento durante las sumas, lo que puede resultar costoso. Una solución típica es representar el número en una base pequeña, b , de modo que, por ejemplo, 8 b sea un entero de máquina representable. Luego se pueden realizar varias adiciones antes de que se produzca un desbordamiento. Cuando el número se vuelve demasiado grande, sumamos parte del mismo al resultado, o trasladamos y asignamos la parte restante a un número menor que b . Este proceso se llama normalización . Richard Brent utilizó este enfoque en su paquete Fortran, MP. ^[2]

Inicialmente, las computadoras usaban un algoritmo muy similar a la multiplicación larga en base 2, pero los procesadores modernos han optimizado los circuitos para multiplicaciones rápidas utilizando algoritmos más eficientes, al precio de una realización de hardware más compleja. ^{[ cita necesaria ]} En base dos, la multiplicación larga a veces se llama "desplazar y sumar" , porque el algoritmo simplifica y simplemente consiste en desplazarse hacia la izquierda (multiplicar por potencias de dos) y sumar. La mayoría de los microprocesadores disponibles actualmente implementan este u otros algoritmos similares (como la codificación Booth ) para varios tamaños de números enteros y de punto flotante en multiplicadores de hardware o en microcódigo . ^{[ cita necesaria ]}

En los procesadores disponibles actualmente, una instrucción de desplazamiento bit a bit suele ser (pero no siempre) más rápida que una instrucción de multiplicación y se puede utilizar para multiplicar (desplazar a la izquierda) y dividir (desplazar a la derecha) por potencias de dos. La multiplicación por una constante y la división por una constante se pueden implementar utilizando una secuencia de desplazamientos y sumas o restas. Por ejemplo, hay varias formas de multiplicar por 10 utilizando únicamente el desplazamiento de bits y la suma.

 (( x  <<  2 )  +  x )  <<  1  # Aquí 10*x se calcula como (x*2^2 + x)*2  ( x  <<  3 )  +  ( x  <<  1 )  # Aquí 10*x se calcula como x*2^3 + x*2

En algunos casos, tales secuencias de cambios y sumas o restas superarán a los multiplicadores de hardware y especialmente a los divisores. Una división por un número de la forma o a menudo se puede convertir en una secuencia tan corta. ${\displaystyle 2^{n}}$ ${\displaystyle 2^{n}\pm 1}$

Algoritmos para multiplicar a mano

Además de la multiplicación larga estándar, existen varios otros métodos que se utilizan para realizar la multiplicación a mano. Dichos algoritmos pueden diseñarse para lograr velocidad, facilidad de cálculo o valor educativo, particularmente cuando no se dispone de computadoras o tablas de multiplicar .

Método de cuadrícula

El método de la cuadrícula (o método de la caja) es un método introductorio a la multiplicación de varios dígitos que a menudo se enseña a los alumnos de la escuela primaria o primaria . Ha sido una parte estándar del currículo nacional de matemáticas de la escuela primaria en Inglaterra y Gales desde finales de los años 1990. ^[3]

Ambos factores se dividen ("dividen") en sus centenas, decenas y unidades, y luego los productos de las partes se calculan explícitamente en una etapa relativamente simple de sólo multiplicación, antes de que estas contribuciones se sumen para dar la respuesta final en una etapa de adición separada.

El cálculo de 34 × 13, por ejemplo, se podría realizar usando la cuadrícula:

 300 40 90 + 12 ———— 442

seguido de la suma para obtener 442, ya sea en una sola suma (ver a la derecha) o formando los totales fila por fila (300 + 40) + (90 + 12) = 340 + 102 = 442.

Este enfoque de cálculo (aunque no necesariamente con la disposición explícita de la cuadrícula) también se conoce como algoritmo de productos parciales . Su esencia es el cálculo de las multiplicaciones simples por separado, dejando todas las sumas para la etapa final de recopilación.

En principio, el método de la cuadrícula se puede aplicar a factores de cualquier tamaño, aunque el número de subproductos se vuelve engorroso a medida que aumenta el número de dígitos. Sin embargo, se considera un método útil y explícito para introducir la idea de multiplicaciones de varios dígitos; y, en una época en la que la mayoría de los cálculos de multiplicación se realizan con una calculadora o una hoja de cálculo, en la práctica puede ser el único algoritmo de multiplicación que algunos estudiantes necesitarán.

Multiplicación de celosía

Primero, configura la cuadrícula marcando sus filas y columnas con los números que se van a multiplicar. Luego, completa los cuadros con los dígitos de las decenas en los triángulos superiores y los dígitos de las unidades en la parte inferior.

Finalmente, sume a lo largo de los tramos diagonales y lleve según sea necesario para obtener la respuesta.

La multiplicación de celosía o tamiz es algorítmicamente equivalente a la multiplicación larga. Requiere la preparación de un entramado (una cuadrícula dibujada en papel) que guía el cálculo y separa todas las multiplicaciones de las sumas . Fue introducido en Europa en 1202 en el Liber Abaci de Fibonacci . Fibonacci describió la operación como mental, utilizando su mano derecha e izquierda para realizar los cálculos intermedios. Matrakçı Nasuh presentó seis variantes diferentes de este método en este libro del siglo XVI, Umdet-ul Hisab. Fue ampliamente utilizado en las escuelas de Enderun en todo el Imperio Otomano. ^[4] Los huesos de Napier , o varillas de Napier, también utilizaban este método, según publicó Napier en 1617, año de su muerte.

Como se muestra en el ejemplo, el multiplicando y el multiplicador se escriben arriba y a la derecha de una red o tamiz. Se encuentra en "Aritmética" de Muhammad ibn Musa al-Khwarizmi , una de las fuentes de Leonardo mencionada por Sigler, autor de "Fibonacci's Liber Abaci", 2002. ^{[ cita necesaria ]}

• Durante la fase de multiplicación, la red se completa con productos de dos dígitos de los dígitos correspondientes que etiquetan cada fila y columna: el dígito de las decenas va en la esquina superior izquierda.
• Durante la fase de suma, la red se suma en las diagonales.
• Finalmente, si es necesaria una fase de acarreo, la respuesta como se muestra en los lados izquierdo e inferior de la red se convierte a la forma normal llevando los dígitos de las decenas como en la suma o multiplicación larga.

Ejemplo

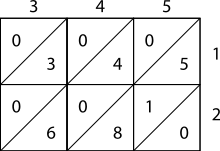
Las imágenes de la derecha muestran cómo calcular 345 × 12 usando la multiplicación reticular. Como ejemplo más complicado, considere la siguiente imagen que muestra el cálculo de 23.958.233 multiplicado por 5.830 (multiplicador); el resultado es 139.676.498.390. Observe que 23.958.233 está en la parte superior de la red y 5.830 está en el lado derecho. Los productos llenan la red y la suma de esos productos (en la diagonal) está en los lados izquierdo e inferior. Luego esas sumas se suman como se muestra.

Multiplicación campesina rusa

El método binario también se conoce como multiplicación campesina, porque ha sido ampliamente utilizado por personas clasificadas como campesinos y, por lo tanto, no han memorizado las tablas de multiplicar necesarias para una multiplicación larga. ^{[5] [ verificación fallida ]} El algoritmo se utilizaba en el antiguo Egipto. ^[6] Sus principales ventajas son que se puede enseñar rápidamente, no requiere memorización y se puede realizar utilizando fichas, como fichas de póquer , si no se dispone de papel y lápiz. La desventaja es que requiere más pasos que una multiplicación larga, por lo que puede resultar difícil de manejar para números grandes.

Descripción

En un papel, escriba en una columna los números que obtiene cuando reduce repetidamente a la mitad el multiplicador, ignorando el resto; en una columna al lado duplica repetidamente el multiplicando. Tacha cada fila en la que el último dígito del primer número sea par y suma los números restantes en la segunda columna para obtener el producto.

Ejemplos

Este ejemplo utiliza la multiplicación campesina para multiplicar 11 por 3 y llegar a un resultado de 33.

Decimal: Binario:11 3 1011 115 6 101 1102 12 10 11001 24 1 11000 —— —————— 33 100001

Describiendo los pasos explícitamente:

• 11 y 3 están escritos en la parte superior.
• 11 se reduce a la mitad (5,5) y 3 se duplica (6). La porción fraccionaria se descarta (5,5 se convierte en 5).
• 5 se reduce a la mitad (2,5) y 6 se duplica (12). La porción fraccionaria se descarta (2,5 se convierte en 2). La cifra de la columna de la izquierda (2) es par , por lo que la cifra de la columna de la derecha (12) se descarta.
• 2 se reduce a la mitad (1) y 12 se duplica (24).
• Todos los valores no tachados se suman: 3 + 6 + 24 = 33.

El método funciona porque la multiplicación es distributiva , entonces:

${\displaystyle {\begin{aligned}3\times 11&=3\times (1\times 2^{0}+1\times 2^{1}+0\times 2^{2}+1\times 2^{3})\\&=3\times (1+2+8)\\&=3+6+24\\&=33.\end{aligned}}}$

Un ejemplo más complicado, utilizando las cifras de los ejemplos anteriores (23.958.233 y 5.830):

Decimal: Binario:5830 23958233 1011011000110 10110110110010010110110012915 47916466 101101100011 101101101100100101101100101457 95832932 10110110001 101101101100100101101100100728 191665864 1011011000 1011011011001001011011001000
364 383331728 101101100 10110110110010010110110010000
182 766663456 10110110 10110110110010010110110010000091 1533326912 1011011 101101101100100101101100100000045 3066653824 101101 1011011011001001011011001000000022 6133307648 10110 10110110110010010110110010000000011 12266615296 1011 10110110110010010110110010000000005 24533230592 101 101101101100100101101100100000000002 49066461184 10 101101101100100101101100100000000000
1 98132922368 1 10110110110010010110110010000000000000 ———————————— 1022143253354344244353353243222210110 (antes de llevar) 139676498390 10000010000101010111100011100111010110

Multiplicación de un cuarto de cuadrado

En algunos casos, se puede utilizar esta fórmula para facilitar la realización de las tareas de multiplicación:

${\displaystyle {\frac {\left(x+y\right)^{2}}{4}}-{\frac {\left(x-y\right)^{2}}{4}}={\frac {1}{4}}\left(\left(x^{2}+2xy+y^{2}\right)-\left(x^{2}-2xy+y^{2}\right)\right)={\frac {1}{4}}\left(4xy\right)=xy.}$

En el caso de que y sean números enteros, tenemos que ${\displaystyle x}$ ${\displaystyle y}$

${\displaystyle (x+y)^{2}\equiv (x-y)^{2}{\bmod {4}}}$

porque y son ambos pares o ambos impares. Esto significa que ${\displaystyle x+y}$ ${\displaystyle x-y}$

${\displaystyle {\begin{aligned}xy&={\frac {1}{4}}(x+y)^{2}-{\frac {1}{4}}(x-y)^{2}\\&=\left((x+y)^{2}{\text{ div }}4\right)-\left((x-y)^{2}{\text{ div }}4\right)\end{aligned}}}$

y es suficiente (pre)calcular la parte integral de cuadrados dividida por 4 como en el siguiente ejemplo.

Ejemplos

A continuación se muestra una tabla de búsqueda de cuartos de cuadrado con el resto descartado para los dígitos del 0 al 18; esto permite la multiplicación de números hasta 9×9 .

Si por ejemplo quisieras multiplicar 9 por 3, observas que la suma y la diferencia son 12 y 6 respectivamente. Si miramos ambos valores en la tabla, obtenemos 36 y 9, cuya diferencia es 27, que es el producto de 9 y 3.

Historia de la multiplicación de un cuarto de cuadrado.

En la época prehistórica, la multiplicación de un cuarto de cuadrado implicaba la función del suelo ; que algunas fuentes ^{[7] [8]} atribuyen a las matemáticas babilónicas (2000-1600 a. C.).

Antoine Voisin publicó una tabla de cuartos de cuadrado del 1 al 1000 en 1817 como ayuda en la multiplicación. Samuel Laundy publicó una tabla más grande de cuartos de cuadrado de 1 a 100.000 en 1856, ^[9] y Joseph Blater publicó una tabla de 1 a 200.000 en 1888. ^[10]

Los multiplicadores de un cuarto de cuadrado se utilizaban en computadoras analógicas para formar una señal analógica que era el producto de dos señales de entrada analógicas. En esta aplicación, la suma y diferencia de dos voltajes de entrada se forman utilizando amplificadores operacionales . El cuadrado de cada uno de ellos se aproxima utilizando circuitos lineales por partes . Finalmente, la diferencia de los dos cuadrados se forma y se escala en un factor de un cuarto utilizando otro amplificador operacional.

En 1980, Everett L. Johnson propuso utilizar el método del cuarto de cuadrado en un multiplicador digital . ^[11] Para formar el producto de dos números enteros de 8 bits, por ejemplo, el dispositivo digital forma la suma y la diferencia, busca ambas cantidades en una tabla de cuadrados, toma la diferencia de los resultados y divide por cuatro desplazando dos bits a la derecha. Para enteros de 8 bits, la tabla de cuartos de cuadrado tendrá 2 ⁹ −1=511 entradas (una entrada para el rango completo 0..510 de sumas posibles, las diferencias usarán solo las primeras 256 entradas en el rango 0..255) o 2 ⁹ −1=511 entradas (utilizando para diferencias negativas la técnica de 2 complementos y enmascaramiento de 9 bits, que evita probar el signo de diferencias), siendo cada entrada de 16 bits de ancho (los valores de las entradas son de (0²/4 )=0 a (510²/4)=65025).

La técnica del multiplicador de un cuarto de cuadrado ha beneficiado a los sistemas de 8 bits que no admiten ningún multiplicador de hardware. Charles Putney implementó esto para el 6502 . ^[12]

Complejidad computacional de la multiplicación.

Problema no resuelto en informática :

¿Cuál es el algoritmo más rápido para la multiplicación de números de dos dígitos? ${\displaystyle n}$

(más problemas sin resolver en informática)

Una línea de investigación en informática teórica trata sobre el número de operaciones aritméticas de un solo bit necesarias para multiplicar números enteros de dos bits. Esto se conoce como complejidad computacional de la multiplicación. Los algoritmos habituales hechos a mano tienen una complejidad asintótica de , pero en 1960 Anatoly Karatsuba descubrió que era posible una mayor complejidad (con el algoritmo de Karatsuba ). ${\displaystyle n}$ ${\displaystyle O(n^{2})}$

Actualmente, el algoritmo con mejor complejidad computacional es un algoritmo de 2019 de David Harvey y Joris van der Hoeven , que utiliza las estrategias de uso de transformaciones de teoría de números introducidas con el algoritmo de Schönhage-Strassen para multiplicar números enteros usando solo operaciones. ^[13] Se conjetura que este es el mejor algoritmo posible, pero se desconocen los límites inferiores. ${\displaystyle O(n\log n)}$ ${\displaystyle \Omega (n\log n)}$

multiplicación de karatsuba

La multiplicación de Karatsuba es un algoritmo de divide y vencerás O( n ^{log ₂ 3} ) ≈ O( n ^1.585 ), que utiliza la recursividad para fusionar subcálculos.

Al reescribir la fórmula, es posible realizar subcálculos/recursividad. Al hacer recursividad, se puede resolver esto de manera rápida.

Sea y representado como cadenas de dígitos en alguna base . Para cualquier entero positivo menor que , se pueden escribir los dos números dados como ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle n}$ ${\displaystyle B}$ ${\displaystyle m}$ ${\displaystyle n}$

${\displaystyle x=x_{1}B^{m}+x_{0},}$

${\displaystyle y=y_{1}B^{m}+y_{0},}$

donde y son menores que . El producto es entonces ${\displaystyle x_{0}}$ ${\displaystyle y_{0}}$ ${\displaystyle B^{m}}$

${\displaystyle {\begin{aligned}xy&=(x_{1}B^{m}+x_{0})(y_{1}B^{m}+y_{0})\\&=x_{1}y_{1}B^{2m}+(x_{1}y_{0}+x_{0}y_{1})B^{m}+x_{0}y_{0}\\&=z_{2}B^{2m}+z_{1}B^{m}+z_{0},\\\end{aligned}}}$

dónde

${\displaystyle z_{2}=x_{1}y_{1},}$

${\displaystyle z_{1}=x_{1}y_{0}+x_{0}y_{1},}$

${\displaystyle z_{0}=x_{0}y_{0}.}$

Estas fórmulas requieren cuatro multiplicaciones y eran conocidas por Charles Babbage . ^[14] Karatsuba observó que se puede calcular en sólo tres multiplicaciones, a costa de algunas sumas adicionales. Con y como antes se puede observar que ${\displaystyle xy}$ ${\displaystyle z_{0}}$ ${\displaystyle z_{2}}$

${\displaystyle {\begin{aligned}z_{1}&=x_{1}y_{0}+x_{0}y_{1}\\&=x_{1}y_{0}+x_{0}y_{1}+x_{1}y_{1}-x_{1}y_{1}+x_{0}y_{0}-x_{0}y_{0}\\&=x_{1}y_{0}+x_{0}y_{0}+x_{0}y_{1}+x_{1}y_{1}-x_{1}y_{1}-x_{0}y_{0}\\&=(x_{1}+x_{0})y_{0}+(x_{0}+x_{1})y_{1}-x_{1}y_{1}-x_{0}y_{0}\\&=(x_{1}+x_{0})(y_{0}+y_{1})-x_{1}y_{1}-x_{0}y_{0}\\&=(x_{1}+x_{0})(y_{1}+y_{0})-z_{2}-z_{0}.\\\end{aligned}}}$

Debido a la sobrecarga de la recursividad, la multiplicación de Karatsuba es más lenta que la multiplicación larga para valores pequeños de n ; Por lo tanto, las implementaciones típicas cambian a una multiplicación larga para valores pequeños de n .

Caso general con multiplicación de N números.

Al explorar patrones después de la expansión, se ve lo siguiente:

${\displaystyle (x_{1}B^{m}+x_{0})(y_{1}B^{m}+y_{0})(z_{1}B^{m}+z_{0})(a_{1}B^{m}+a_{0})=}$
${\displaystyle a_{1}x_{1}y_{1}z_{1}B^{4m}+a_{1}x_{1}y_{1}z_{0}B^{3m}+a_{1}x_{1}y_{0}z_{1}B^{3m}+a_{1}x_{0}y_{1}z_{1}B^{3m}}$
${\displaystyle +a_{0}x_{1}y_{1}z_{1}B^{3m}+a_{1}x_{1}y_{0}z_{0}B^{2m}+a_{1}x_{0}y_{1}z_{0}B^{2m}+a_{0}x_{1}y_{1}z_{0}B^{2m}}$
${\displaystyle +a_{1}x_{0}y_{0}z_{1}B^{2m}+a_{0}x_{1}y_{0}z_{1}B^{2m}+a_{0}x_{0}y_{1}z_{1}B^{2m}+a_{1}x_{0}y_{0}z_{0}B^{m}}$
${\displaystyle +a_{0}x_{1}y_{0}z_{0}B^{m}+a_{0}x_{0}y_{1}z_{0}B^{m}+a_{0}x_{0}y_{0}z_{1}B^{m}+a_{0}x_{0}y_{0}z_{0}}$

Cada sumando está asociado a un número binario único de 0 a , por ejemplo , etc. Además; B se potencia al número 1, en esta cadena binaria, multiplicado por m. ${\displaystyle 2^{N+1}-1}$ ${\displaystyle a_{1}x_{1}y_{1}z_{1}\longleftrightarrow 1111,\ a_{1}x_{0}y_{1}z_{0}\longleftrightarrow 1010}$

Si expresamos esto en menos términos, obtenemos:

${\displaystyle \prod _{j=1}^{N}(x_{j,1}B^{m}+x_{j,0})=\sum _{i=1}^{2^{N+1}-1}\prod _{j=1}^{N}x_{j,c(i,j)}B^{m\sum _{j=1}^{N}c(i,j)}=\sum _{j=0}^{N}z_{j}B^{jm}}$, donde significa dígito en el número i en la posición j. Darse cuenta de ${\displaystyle c(i,j)}$ ${\displaystyle c(i,j)\in \{0,1\}}$

${\displaystyle z_{0}=\prod _{j=1}^{N}x_{j,0}}$
${\displaystyle z_{N}=\prod _{j=1}^{N}x_{j,1}}$
${\displaystyle z_{N-1}=\prod _{j=1}^{N}(x_{j,0}+x_{j,1})-\sum _{i\neq N-1}^{N}z_{i}}$

Historia

El algoritmo de Karatsuba fue el primer algoritmo conocido para la multiplicación que es asintóticamente más rápido que la multiplicación larga ^[15] y, por lo tanto, puede verse como el punto de partida para la teoría de las multiplicaciones rápidas.

toom-cocinar

Otro método de multiplicación se llama Toom-Cook o Toom-3. El método Toom-Cook divide cada número para multiplicarlo en varias partes. El método Toom-Cook es una de las generalizaciones del método Karatsuba. Un Toom-Cook de tres vías puede hacer una multiplicación de tamaño 3N por el costo de cinco multiplicaciones de tamaño N. Esto acelera la operación en un factor de 9/5, mientras que el método Karatsuba la acelera en 4/3.

Aunque usar cada vez más partes puede reducir aún más el tiempo dedicado a multiplicaciones recursivas, los gastos generales de las sumas y la gestión de dígitos también aumentan. Por esta razón, el método de las transformadas de Fourier suele ser más rápido para números con varios miles de dígitos y asintóticamente más rápido para números aún mayores.

Schönhage-Strassen

Demostración de cómo multiplicar 1234 × 5678 = 7006652 usando transformadas rápidas de Fourier (FFT). Se utilizan transformaciones de teoría de números en los números enteros módulo 337, seleccionando 85 como raíz octava de la unidad. Se utiliza la base 10 en lugar de la base 2 ^w con fines ilustrativos.

Todo número en base B se puede escribir como un polinomio:

${\displaystyle X=\sum _{i=0}^{N}{x_{i}B^{i}}}$

Además, la multiplicación de dos números podría considerarse como el producto de dos polinomios:

${\displaystyle XY=(\sum _{i=0}^{N}{x_{i}B^{i}})(\sum _{j=0}^{N}{y_{i}B^{j}})}$

Porque, para :, tenemos una convolución. ${\displaystyle B^{k}}$ ${\displaystyle c_{k}=\sum _{(i,j):i+j=k}{a_{i}b_{j}}=\sum _{i=0}^{k}{a_{i}b_{k-i}}}$

Al usar fft (transformación rápida de Fourier) con regla de convolución, podemos obtener

${\displaystyle {\hat {f}}(a*b)={\hat {f}}(\sum _{i=0}^{k}{a_{i}b_{k-i}})={\hat {f}}(a)}$● . Eso es; ● , donde es el coeficiente correspondiente en el espacio de Fourier. Esto también se puede escribir como: fft(a * b) = fft(a) ● fft(b). ${\displaystyle {\hat {f}}(b)}$ ${\displaystyle C_{k}=a_{k}}$ ${\displaystyle b_{k}}$ ${\displaystyle C_{k}}$

Tenemos el mismo coeficiente debido a la linealidad bajo la transformación de Fourier y porque estos polinomios solo constan de un término único por coeficiente:

${\displaystyle {\hat {f}}(x^{n})=\left({\frac {i}{2\pi }}\right)^{n}\delta ^{(n)}}$ y ${\displaystyle {\hat {f}}(a\,X(\xi )+b\,Y(\xi ))=a\,{\hat {X}}(\xi )+b\,{\hat {Y}}(\xi )}$

Regla de convolución: ● ${\displaystyle {\hat {f}}(X*Y)=\ {\hat {f}}(X)}$ ${\displaystyle {\hat {f}}(Y)}$

Hemos reducido nuestro problema de convolución a un problema de producto, mediante fft.

Al encontrar ifft (interpolación polinómica), para cada uno , se obtienen los coeficientes deseados. ${\displaystyle c_{k}}$

El algoritmo utiliza la estrategia de dividir y conquistar para dividir el problema en subproblemas.

Tiene una complejidad temporal de O ( n  log( n ) log(log( n ))).

Historia

Los algoritmos fueron inventados por Strassen (1968). El algoritmo se hizo práctico y Schönhage y Strassen proporcionaron garantías teóricas en 1971, lo que dio como resultado el algoritmo de Schönhage-Strassen . ^[dieciséis]

Futuras mejoras

En 2007, el matemático suizo Martin Fürer de la Universidad Estatal de Pensilvania mejoró la complejidad asintótica de la multiplicación de enteros a n  log( n ) 2 ^{Θ( log * ( n ) )} utilizando transformadas de Fourier sobre números complejos , ^[17] donde log ^* denota el logaritmo iterado . Anindya De, Chandan Saha, Piyush Kurur y Ramprasad Saptharishi dieron un algoritmo similar utilizando aritmética modular en 2008 logrando el mismo tiempo de ejecución. ^[18] En el contexto del material anterior, lo que estos últimos autores han logrado es encontrar N mucho menor que 2 ^{3 k} + 1, de modo que Z / NZ tiene una raíz unitaria (2 m ). Esto acelera el cálculo y reduce la complejidad del tiempo. Sin embargo, estos últimos algoritmos sólo son más rápidos que los de Schönhage-Strassen para entradas imprácticamente grandes.

En 2014, Harvey, Joris van der Hoeven y Lecerf ^[19] dieron un nuevo algoritmo que logra un tiempo de ejecución de , haciendo explícita la constante implícita en el exponente. También propusieron una variante de su algoritmo que logra pero cuya validez se basa en conjeturas estándar sobre la distribución de los números primos de Mersenne . En 2016, Covanov y Thomé propusieron un algoritmo de multiplicación de enteros basado en una generalización de los números primos de Fermat que, conjeturalmente, alcanza un límite de complejidad de . Esto coincide con el resultado condicional de 2015 de Harvey, van der Hoeven y Lecerf, pero utiliza un algoritmo diferente y se basa en una conjetura diferente. ^[20] En 2018, Harvey y van der Hoeven utilizaron un enfoque basado en la existencia de vectores reticulares cortos garantizados por el teorema de Minkowski para demostrar un límite de complejidad incondicional de . ^[21] ${\displaystyle O(n\log n\cdot 2^{3\log ^{*}n})}$ ${\displaystyle O(\log ^{*}n)}$ ${\displaystyle O(n\log n\cdot 2^{2\log ^{*}n})}$ ${\displaystyle O(n\log n\cdot 2^{2\log ^{*}n})}$ ${\displaystyle O(n\log n\cdot 2^{2\log ^{*}n})}$

En marzo de 2019, David Harvey y Joris van der Hoeven anunciaron el descubrimiento de un algoritmo de multiplicación O ( n log n ) . ^[22] Se publicó en Annals of Mathematics en 2021. ^[23] Debido a que Schönhage y Strassen predijeron que n  log( n ) es el "mejor resultado posible", Harvey dijo: "...  se espera que nuestro trabajo sea el "Es el final del camino para este problema, aunque todavía no sabemos cómo demostrarlo rigurosamente". ^[24]

límites inferiores

Existe un límite inferior trivial de Ω ( n ) para multiplicar dos números de n bits en un solo procesador; no se conoce ningún algoritmo de coincidencia (en máquinas convencionales, es decir, en máquinas equivalentes de Turing) ni ningún límite inferior más definido. La multiplicación se encuentra fuera de AC ⁰ [ p ] para cualquier p primo , lo que significa que no existe una familia de circuitos de tamaño polinómico (o incluso subexponencial) de profundidad constante que utilicen puertas AND, OR, NOT y MOD _p que puedan calcular un producto. Esto se deriva de una reducción en profundidad constante de MOD _q a la multiplicación. ^[25] Los límites inferiores para la multiplicación también son conocidos para algunas clases de programas de ramificación . ^[26]

Multiplicación de números complejos

La multiplicación compleja normalmente implica cuatro multiplicaciones y dos sumas.

${\displaystyle (a+bi)(c+di)=(ac-bd)+(bc+ad)i.}$

O

${\displaystyle {\begin{array}{c|c|c}\times &a&bi\\\hline c&ac&bci\\\hline di&adi&-bd\end{array}}}$

Como observó Peter Ungar en 1963, se puede reducir el número de multiplicaciones a tres, utilizando esencialmente el mismo cálculo que el algoritmo de Karatsuba . ^[27] El producto ( a  +  bi ) · ( c  +  di ) se puede calcular de la siguiente manera.

k ₁ = c · ( a + b )

k ₂ = a · ( re - c )

k ₃ = segundo · ( c + re )

Parte real = k ₁ − k ₃

Parte imaginaria = k ₁ + k ₂ .

Este algoritmo utiliza sólo tres multiplicaciones, en lugar de cuatro, y cinco sumas o restas en lugar de dos. Si una multiplicación es más cara que tres sumas o restas, como cuando se calcula a mano, entonces se gana en velocidad. En las computadoras modernas, multiplicar y sumar pueden tomar aproximadamente el mismo tiempo, por lo que es posible que no haya ganancia de velocidad. Existe una contrapartida en el sentido de que puede haber cierta pérdida de precisión al utilizar punto flotante.

Para las transformadas rápidas de Fourier (FFT) (o cualquier transformación lineal ), las multiplicaciones complejas se realizan mediante coeficientes constantes c  +  di (llamados factores de giro en FFT), en cuyo caso dos de las sumas ( d − c y c + d ) se pueden calcular previamente. . Por lo tanto, sólo se requieren tres multiplicaciones y tres sumas. ^[28] Sin embargo, intercambiar una multiplicación por una suma de esta manera puede que ya no sea beneficioso con las unidades modernas de punto flotante . ^[29]

Multiplicación de polinomios

Todos los algoritmos de multiplicación anteriores también se pueden ampliar para multiplicar polinomios . Alternativamente , se puede utilizar la técnica de sustitución de Kronecker para convertir el problema de multiplicar polinomios en una única multiplicación binaria. ^[30]

Los métodos de multiplicación largos se pueden generalizar para permitir la multiplicación de fórmulas algebraicas:

14ac - 3ab + 2 multiplicado por ac - ab + 1

14ac -3ab 2 ca-ab 1 ————————————————————— 14a 2 c 2 -3a 2 aC 2ac -14a 2 aC 3 a 2 b 2 -2ab 14ac -3ab 2 ———————————————————————————————————————— 14a 2 c 2 -17a 2 aC 16ac 3a 2 b 2 -5ab +2 ========================================= [31]

Como ejemplo adicional de multiplicación basada en columnas, considere multiplicar 23 toneladas largas (t), 12 quintales (cwt) y 2 cuartos (qtr) por 47. Este ejemplo utiliza medidas avoirdupois : 1 t = 20 cwt, 1 cwt = 4 qtr.

 t cwt qtr 23 12 2 47x ———————————————— 141 94 94 940 470 29 23 ———————————————— 1110 587 94 ———————————————— 1110 7 2 ================= Respuesta: 1110 toneladas 7 cwt 2 cuartos

Primero multiplica los cuartos por 47, el resultado 94 se escribe en el primer espacio de trabajo. Luego, multiplica cwt 12*47 = (2 + 10)*47 pero no sumes los resultados parciales (94, 470) todavía. Asimismo, multiplique 23 por 47 para obtener (141, 940). Se suma la columna de cuartos y el resultado se coloca en el segundo espacio de trabajo (un movimiento trivial en este caso). 94 quarters son 23 cwt y 2 qtr, así que coloque el 2 en la respuesta y coloque el 23 en la siguiente columna de la izquierda. Ahora suma las tres entradas en la columna cwt dando 587. Esto es 29 t 7 cwt, así que escribe el 7 en la respuesta y el 29 en la columna de la izquierda. Ahora suma la columna de toneladas. No es necesario realizar ningún ajuste, por lo que el resultado simplemente se copia.

Se pueden utilizar el mismo diseño y métodos para cualquier medida tradicional y monedas no decimales, como el antiguo sistema británico £sd .

Ver también

• multiplicador binario
• multiplicador de papá
• Algoritmo de división
• Esquema de Horner para la evaluación de un polinomio.
• Logaritmo
• Cálculo mental
• Transformada de teoría de números
• Prostaféresis
• Regla de cálculo
• sistema de Trachtenberg
• Sistema de números residuales § Multiplicación para otro algoritmo de multiplicación rápido, especialmente eficiente cuando se realizan muchas operaciones en secuencia, como en álgebra lineal.
• Árbol de Wallace

Referencias

1. "Multiplicación". www.mathematische-basteleien.de . Consultado el 15 de marzo de 2022 .
2. Brent, Richard P (marzo de 1978). "Un paquete aritmético de precisión múltiple de Fortran". Transacciones ACM sobre software matemático . 4 : 57–70. CiteSeerX 10.1.1.117.8425 . doi :10.1145/355769.355775. S2CID  8875817. 
3. Eason, Gary (13 de febrero de 2000). "Regreso al cole para padres". Noticias de la BBC .
   Eastaway, Rob (10 de septiembre de 2010). "Por qué los padres no pueden hacer matemáticas hoy". Noticias de la BBC.
4. Corlu, MS; Burlbaw, LM; Capraro, RM; Corlu, MA; Han, S. (2010). "La escuela del palacio otomano Enderun y el hombre con múltiples talentos, Matrakçı Nasuh". Revista de la Sociedad Coreana de Educación Matemática Serie D: Investigación en Educación Matemática . 14 (1): 19–31.
5. Bogomolny, Alejandro . "Multiplicación campesina". www.cut-the-knot.org . Consultado el 4 de noviembre de 2017 .
6. Wells, D. (1987). Diccionario pingüino de números curiosos e interesantes . Libros de pingüinos. pag. 44.ISBN​ 978-0-14-008029-2.
7. McFarland, David (2007), Tablas trimestrales revisadas: tablas anteriores, división del trabajo en la construcción de mesas e implementaciones posteriores en computadoras analógicas, p. 1
8. Robson, Leonor (2008). Matemáticas en el antiguo Irak: una historia social . Prensa de la Universidad de Princeton. pag. 227.ISBN​ 978-0691201405.
9. "Reseñas", The Civil Engineer and Architect's Journal : 54–55, 1857.
10. Holmes, Neville (2003), "Multiplicar con cuartos de cuadrados", The Mathematical Gazette , 87 (509): 296–299, doi :10.1017/S0025557200172778, JSTOR  3621048, S2CID  125040256.
11. Everett L., Johnson (marzo de 1980), "Un multiplicador de cuarto de cuadrado digital", IEEE Transactions on Computers , vol. C-29, núm. 3, Washington, DC, EE.UU.: IEEE Computer Society, págs. 258–261, doi :10.1109/TC.1980.1675558, ISSN  0018-9340, S2CID  24813486
12. Putney, Charles (marzo de 1986). "La multiplicación 6502 más rápida hasta ahora". Línea de montaje de Apple . 6 (6).
13. Harvey, David; van der Hoeven, Joris (2021). "Multiplicación de enteros en el tiempo O ( n log ⁡ n ) {\displaystyle O(n\log n)} " (PDF) . Anales de Matemáticas . Segunda Serie. 193 (2): 563–617. doi : 10.4007/anales.2021.193.2.4. SEÑOR  4224716. S2CID  109934776.
14. Charles Babbage, Capítulo VIII - De la máquina analítica, números más grandes tratados, pasajes de la vida de un filósofo, Longman Green, Londres, 1864; página 125.
15. D. Knuth, El arte de la programación informática , vol. 2 segundos. 4.3.3 (1998)
16. Schönhage, A.; Strassen, V. (1971). "Schnelle Multiplication großer Zahlen". Informática . 7 (3–4): 281–292. doi :10.1007/BF02242355. S2CID  9738629.
17. Furer, M. (2007). "Multiplicación de enteros más rápida" (PDF) . Actas del trigésimo noveno simposio anual de ACM sobre teoría de la informática, 11 al 13 de junio de 2007, San Diego, California, EE. UU . págs. 57–66. doi :10.1145/1250790.1250800. ISBN 978-1-59593-631-8. S2CID  8437794.
18. De, A.; Saha, C.; Kurur, P.; Saptharishi, R. (2008). "Multiplicación rápida de enteros mediante aritmética modular". Actas del 40º Simposio anual ACM sobre Teoría de la Computación (STOC) . págs. 499–506. arXiv : 0801.1416 . doi :10.1145/1374376.1374447. ISBN 978-1-60558-047-0. S2CID  3264828.
19. Harvey, David; van der Hoeven, Joris; Lecerf, Grégoire (2016). "Multiplicación de enteros aún más rápida". Revista de Complejidad . 36 : 1–30. arXiv : 1407.3360 . doi :10.1016/j.jco.2016.03.001. SEÑOR  3530637.
20. Covanov, Sviatoslav; Thomé, Emmanuel (2019). "Multiplicación rápida de enteros utilizando números primos de Fermat generalizados". Matemáticas. comp. 88 (317): 1449-1477. arXiv : 1502.02800 . doi : 10.1090/mcom/3367. S2CID  67790860.
21. Harvey, D.; van der Hoeven, J. (2019). "Multiplicación de enteros más rápida utilizando vectores de red cortos". La serie de libros abiertos . 2 : 293–310. arXiv : 1802.07932 . doi :10.2140/obs.2019.2.293. S2CID  3464567.
22. Hartnett, Kevin (11 de abril de 2019). "Los matemáticos descubren la forma perfecta de multiplicar". Revista Quanta . Consultado el 3 de mayo de 2019 .
23. Harvey, David; van der Hoeven, Joris (2021). "Multiplicación de enteros en el tiempo O ( n log ⁡ n ) {\displaystyle O(n\log n)} " (PDF) . Anales de Matemáticas . Segunda Serie. 193 (2): 563–617. doi : 10.4007/anales.2021.193.2.4. SEÑOR  4224716. S2CID  109934776.
24. Gilbert, Lachlan (4 de abril de 2019). "El genio de las matemáticas resuelve un problema de multiplicación de 48 años". UNSW . Consultado el 18 de abril de 2019 .
25. Arora, Sanjeev; Barac, Booz (2009). Complejidad computacional: un enfoque moderno. Prensa de la Universidad de Cambridge. ISBN 978-0-521-42426-4.
26. Ablayev, F.; Karpinski, M. (2003). "Un límite inferior para la multiplicación de enteros en programas de ramificación de una sola lectura ordenados aleatorios" (PDF) . Información y Computación . 186 (1): 78–89. doi :10.1016/S0890-5401(03)00118-4.
27. Knuth, Donald E. (1988), El arte de la programación informática volumen 2: algoritmos seminuméricos , Addison-Wesley , págs.519, 706
28. Duhamel, P.; Vetterli, M. (1990). "Transformaciones rápidas de Fourier: una revisión del tutorial y un estado del arte" (PDF) . Procesamiento de la señal . 19 (4): 259–299 Véase la sección 4.1. doi :10.1016/0165-1684(90)90158-U.
29. Johnson, SG; Frigo, M. (2007). "Una FFT de base dividida modificada con menos operaciones aritméticas" (PDF) . Traducción IEEE. Proceso de señal . 55 (1): 111–9 Véase la Sección IV. Código Bib : 2007ITSP...55..111J. doi :10.1109/TSP.2006.882087. S2CID  14772428.
30. von zur Gathen, Joaquín ; Gerhard, Jürgen (1999), Álgebra informática moderna, Cambridge University Press, págs. 243–244, ISBN 978-0-521-64176-0.
31. Castillo, Frank (1900). Taller de Matemáticas. Londres: MacMillan and Co. p. 74.

Otras lecturas

• Warren Jr., Henry S. (2013). El placer del hacker (2 ed.). Addison Wesley - Pearson Education, Inc. ISBN 978-0-321-84268-8.
• Savard, John JG (2018) [2006]. "Técnicas Aritméticas Avanzadas". cuadribloc . Archivado desde el original el 3 de julio de 2018 . Consultado el 16 de julio de 2018 .
• Johansson, Kenny (2008). Computaciones basadas en cambios y sumas de baja potencia y complejidad (PDF) (tesis de disertación). Estudios de Linköping en ciencia y tecnología (1 ed.). Linköping, Suecia: Departamento de Ingeniería Eléctrica, Universidad de Linköping . ISBN 978-91-7393-836-5. ISSN  0345-7524. No. 1201. Archivado (PDF) desde el original el 13 de agosto de 2017 . Consultado el 23 de agosto de 2021 .(x+268 páginas)

enlaces externos

Aritmética básica

• Las muchas formas de aritmética en las matemáticas cotidianas de la UCSMP
• Una presentación en PowerPoint sobre matemáticas antiguas.
• Video Flash de multiplicación de celosía

Algoritmos avanzados

• Algoritmos de multiplicación utilizados por GMP