
La fuerza g o fuerza gravitatoria equivalente es la fuerza específica de la masa (fuerza por unidad de masa), expresada en unidades de gravedad estándar (símbolo g o g 0 , que no debe confundirse con "g", el símbolo de gramos ). Se utiliza para aceleraciones sostenidas , que causan una percepción de peso . Por ejemplo, un objeto en reposo sobre la superficie de la Tierra está sujeto a 1 g , que equivale al valor convencional de la aceleración gravitatoria en la Tierra, aproximadamente9,8 m/s 2 . [1] Una aceleración más transitoria, acompañada de un tirón significativo , se denomina choque . [ cita requerida ]
Cuando la fuerza g se produce cuando la superficie de un objeto es empujada por la superficie de otro objeto, la fuerza de reacción a este empuje produce una fuerza igual y opuesta por cada unidad de masa de cada objeto. Los tipos de fuerzas involucradas se transmiten a través de los objetos mediante tensiones mecánicas internas . La aceleración gravitacional es una de las causas de la aceleración de un objeto en relación con la caída libre . [2] [3]
La fuerza g que experimenta un objeto se debe a la suma vectorial de todas las fuerzas gravitacionales y no gravitacionales que actúan sobre la libertad de movimiento de un objeto. En la práctica, como se ha señalado, se trata de fuerzas de contacto superficial entre objetos. Dichas fuerzas provocan tensiones y deformaciones en los objetos, ya que deben transmitirse desde una superficie del objeto. Debido a estas deformaciones, las fuerzas g elevadas pueden ser destructivas.
Por ejemplo, una fuerza de 1 g sobre un objeto que se encuentra sobre la superficie de la Tierra es causada por la fuerza mecánica ejercida en dirección ascendente por el suelo , evitando que el objeto caiga libremente. La fuerza de contacto ascendente del suelo garantiza que un objeto en reposo sobre la superficie de la Tierra se acelere en relación con la condición de caída libre. (La caída libre es la trayectoria que seguiría el objeto al caer libremente hacia el centro de la Tierra). La tensión dentro del objeto está asegurada por el hecho de que las fuerzas de contacto con el suelo se transmiten solo desde el punto de contacto con el suelo.
Los objetos que caen libremente en una trayectoria inercial , bajo la influencia de la gravedad únicamente, no sienten fuerza g, una condición conocida como ingravidez . Estar en caída libre en una trayectoria inercial se denomina coloquialmente "gravedad cero " , que es la abreviatura de "fuerza g cero". Las condiciones de fuerza g cero se darían dentro de un ascensor que cayera libremente hacia el centro de la Tierra (en el vacío) o (con una buena aproximación) dentro de una nave espacial en órbita terrestre . Estos son ejemplos de aceleración de coordenadas (un cambio en la velocidad) sin sensación de peso.
En ausencia de campos gravitatorios, o en direcciones perpendiculares a ellos, las aceleraciones propias y coordinadas son las mismas, y cualquier aceleración coordinada debe ser producida por una aceleración de fuerza g correspondiente. Un ejemplo de esto es un cohete en el espacio libre: cuando los motores producen cambios simples en la velocidad, esos cambios causan fuerzas g sobre el cohete y los pasajeros.
La unidad de medida de la aceleración en el Sistema Internacional de Unidades (SI) es m/s 2 . [4] Sin embargo, para distinguir la aceleración relativa a la caída libre de la aceleración simple (tasa de cambio de velocidad), a menudo se utiliza la unidad g . Una g es la fuerza por unidad de masa debida a la gravedad en la superficie de la Tierra y es la gravedad estándar (símbolo: g n ), definida como9.806 65 metros por segundo al cuadrado , [5] o equivalente9,806 65 newtons de fuerza por kilogramo de masa. La definición de la unidad no varía según la ubicación: la fuerza g cuando se está de pie en la Luna es casi exactamente 1 ⁄ 6 de la que se encuentra en la Tierra. La unidad g no es una de las unidades del SI, que utiliza "g" para el gramo. Además, " g " no debe confundirse con " G ", que es el símbolo estándar para la constante gravitacional . [6] Esta notación se utiliza comúnmente en la aviación, especialmente en la aviación militar acrobática o de combate, para describir las fuerzas aumentadas que deben superar los pilotos para permanecer conscientes y no g-LOC ( pérdida de conciencia inducida por g ). [7]
La medición de la fuerza g se realiza normalmente con un acelerómetro (consulte la explicación más adelante en la sección "Medición con un acelerómetro"). En ciertos casos, las fuerzas g se pueden medir con básculas calibradas adecuadamente.
El término "fuerza" g es técnicamente incorrecto, ya que es una medida de aceleración , no de fuerza. Si bien la aceleración es una cantidad vectorial , las aceleraciones de fuerza g ("fuerzas g" para abreviar) a menudo se expresan como un escalar , basado en la magnitud vectorial, con fuerzas g positivas apuntando hacia abajo (indicando aceleración hacia arriba) y fuerzas g negativas apuntando hacia arriba. Por lo tanto, una fuerza g es un vector de aceleración. Es una aceleración que debe ser producida por una fuerza mecánica y no puede ser producida por la simple gravitación. Los objetos sobre los que actúa solo la gravitación no experimentan (o "sienten") ninguna fuerza g y carecen de peso. Las fuerzas g, cuando se multiplican por una masa sobre la que actúan, se asocian con un cierto tipo de fuerza mecánica en el sentido correcto del término "fuerza", y esta fuerza produce tensión de compresión y tensión de tracción . Tales fuerzas dan como resultado la sensación operativa de peso, pero la ecuación conlleva un cambio de signo debido a la definición de peso positivo en la dirección hacia abajo, por lo que la dirección de peso-fuerza es opuesta a la dirección de aceleración de fuerza g:
La razón del signo menos es que la fuerza real (es decir, el peso medido) sobre un objeto producida por una fuerza g está en la dirección opuesta al signo de la fuerza g, ya que en física, el peso no es la fuerza que produce la aceleración, sino más bien la fuerza de reacción igual y opuesta a ella. Si la dirección hacia arriba se toma como positiva (la convención cartesiana normal), entonces la fuerza g positiva (un vector de aceleración que apunta hacia arriba) produce una fuerza/peso sobre cualquier masa, que actúa hacia abajo (un ejemplo es la aceleración g positiva del lanzamiento de un cohete, que produce peso hacia abajo). De la misma manera, una fuerza g negativa es un vector de aceleración hacia abajo (la dirección negativa en el eje y), y esta aceleración hacia abajo produce una fuerza de peso en una dirección hacia arriba (por lo tanto, tirando de un piloto hacia arriba fuera del asiento y forzando la sangre hacia la cabeza de un piloto orientado normalmente).
Si una fuerza g (aceleración) es verticalmente ascendente y es aplicada por el suelo (que se acelera a través del espacio-tiempo) o aplicada por el piso de un ascensor a una persona de pie, la mayor parte del cuerpo experimenta una tensión de compresión que, a cualquier altura, si se multiplica por el área, es la fuerza mecánica relacionada, que es el producto de la fuerza g por la masa soportada (la masa por encima del nivel de soporte, incluidos los brazos que cuelgan por encima de ese nivel). Al mismo tiempo, los propios brazos experimentan una tensión de tracción, que a cualquier altura, si se multiplica por el área, es nuevamente la fuerza mecánica relacionada, que es el producto de la fuerza g por la masa que cuelga por debajo del punto de soporte mecánico. La fuerza de resistencia mecánica se propaga desde los puntos de contacto con el piso o la estructura de soporte, y disminuye gradualmente hasta cero en los extremos sin soporte (la parte superior en el caso de soporte desde abajo, como un asiento o el piso, la parte inferior para una parte colgante del cuerpo u objeto). Con la fuerza de compresión contada como fuerza de tracción negativa, la tasa de cambio de la fuerza de tracción en la dirección de la fuerza g, por unidad de masa (el cambio entre partes del objeto tal que la porción del objeto entre ellas tiene masa unitaria), es igual a la fuerza g más las fuerzas externas no gravitacionales sobre la porción, si las hay (contadas como positivas en la dirección opuesta a la fuerza g).
Para una fuerza g dada, las tensiones son las mismas, independientemente de si esta fuerza g es causada por la resistencia mecánica a la gravedad, o por una aceleración de coordenadas (cambio en la velocidad) causada por una fuerza mecánica, o por una combinación de estas. Por lo tanto, para las personas todas las fuerzas mecánicas se sienten exactamente igual, ya sea que causen aceleración de coordenadas o no. Para los objetos, de manera similar, la cuestión de si pueden soportar la fuerza g mecánica sin sufrir daños es la misma para cualquier tipo de fuerza g. Por ejemplo, la aceleración hacia arriba (por ejemplo, aumento de velocidad al subir o disminución de velocidad al bajar) en la Tierra se siente igual que estar estacionario en un cuerpo celeste con una gravedad superficial más alta . La gravitación actuando sola no produce ninguna fuerza g; la fuerza g solo se produce a partir de empujones y tirones mecánicos. Para un cuerpo libre (uno que es libre de moverse en el espacio), tales fuerzas g solo surgen cuando se modifica la trayectoria "inercial" que es el efecto natural de la gravitación, o el efecto natural de la inercia de la masa. Tal modificación solo puede surgir de influencias distintas a la gravitación.
Algunos ejemplos de situaciones importantes que involucran fuerzas g incluyen:
Un ejemplo clásico de fuerza g negativa es el de una montaña rusa totalmente invertida que acelera (cambia de velocidad) hacia el suelo. En este caso, los pasajeros de la montaña rusa son acelerados hacia el suelo más rápido de lo que los aceleraría la gravedad y, por lo tanto, quedan atrapados boca abajo en sus asientos. En este caso, la fuerza mecánica ejercida por el asiento causa la fuerza g al alterar la trayectoria del pasajero hacia abajo de una manera que difiere de la aceleración gravitacional. La diferencia en el movimiento hacia abajo, ahora más rápido de lo que proporcionaría la gravedad, es causada por el empuje del asiento y da como resultado una fuerza g hacia el suelo.
Todas las "aceleraciones coordinadas" (o la falta de ellas), se describen mediante las leyes del movimiento de Newton de la siguiente manera:
La segunda ley del movimiento , la ley de la aceleración, establece que F = ma , lo que significa que una fuerza F que actúa sobre un cuerpo es igual a la masa m del cuerpo multiplicada por su aceleración a .
La tercera ley del movimiento , la ley de las acciones recíprocas, establece que todas las fuerzas se dan en pares, y que estas dos fuerzas son iguales en magnitud y opuestas en dirección. La tercera ley del movimiento de Newton significa que no solo la gravedad se comporta como una fuerza que actúa hacia abajo sobre, por ejemplo, una piedra sostenida en la mano, sino que también la piedra ejerce una fuerza sobre la Tierra, igual en magnitud y opuesta en dirección.

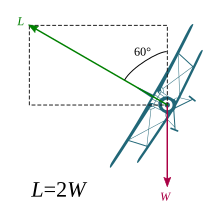
En un avión, el asiento del piloto puede considerarse como la mano que sostiene la roca, y el piloto como la roca. Cuando vuela recto y nivelado a 1 g , el piloto se ve afectado por la fuerza de la gravedad. Su peso (una fuerza hacia abajo) es de 725 newtons (163 lb f ). De acuerdo con la tercera ley de Newton, el avión y el asiento debajo del piloto proporcionan una fuerza igual y opuesta que empuja hacia arriba con una fuerza de 725 N. Esta fuerza mecánica proporciona la aceleración propia hacia arriba de 1,0 g sobre el piloto, aunque esta velocidad en la dirección ascendente no cambia (esto es similar a la situación de una persona parada en el suelo, donde el suelo proporciona esta fuerza y esta fuerza g).
Si el piloto de repente tirara de la palanca hacia atrás y acelerara su avión hacia arriba a 9,8 m/s2 , la fuerza g total sobre su cuerpo sería de 2 g , la mitad de la cual proviene del asiento que empuja al piloto para resistir la gravedad, y la otra mitad del asiento que empuja al piloto para provocar su aceleración hacia arriba, un cambio en la velocidad que también es una aceleración propia porque también difiere de una trayectoria de caída libre. Considerado en el marco de referencia del avión, su cuerpo ahora está generando una fuerza de 1450 N (330 lb f ) hacia abajo en su asiento y el asiento está empujando simultáneamente hacia arriba con una fuerza igual de 1450 N.
Siempre que alguien viaja en un vehículo, se experimenta una aceleración sin oposición debida a fuerzas mecánicas y, en consecuencia, a la fuerza g, ya que siempre provoca una aceleración adecuada y (en ausencia de gravedad) también una aceleración coordinada (cuando cambia la velocidad). Siempre que el vehículo cambia de dirección o de velocidad, los ocupantes sienten fuerzas laterales (de lado a lado) o longitudinales (hacia adelante y hacia atrás) producidas por el empuje mecánico de sus asientos.
La expresión "1 g =9.806 65 m/s 2 " significa que por cada segundo que transcurre, la velocidad cambia9.806 65 metros por segundo (35.303 94 km/h ). Esta tasa de cambio de velocidad también se puede denotar como9.806 65 (metros por segundo) por segundo, o9.806 65 m/s 2 . Por ejemplo: una aceleración de 1 g equivale a una tasa de cambio en la velocidad de aproximadamente 35 km/h (22 mph) por cada segundo que transcurre. Por lo tanto, si un automóvil es capaz de frenar a 1 g y viaja a 35 km/h, puede frenar hasta detenerse en un segundo y el conductor experimentará una desaceleración de 1 g . El automóvil que viaja al triple de esta velocidad, 105 km/h (65 mph), puede frenar hasta detenerse en tres segundos.
En el caso de un aumento de velocidad de 0 a v con aceleración constante dentro de una distancia de s, esta aceleración es v 2 /(2 s ).
La preparación de un objeto para la tolerancia g (que no se dañe cuando se lo somete a una fuerza g alta) se denomina endurecimiento g. [ cita requerida ] Esto puede aplicarse, por ejemplo, a los instrumentos en un proyectil disparado por un arma.
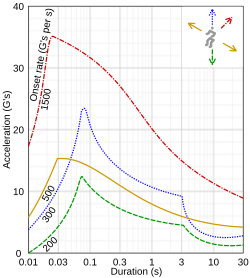
Las tolerancias humanas dependen de la magnitud de la fuerza gravitacional, el tiempo durante el cual se aplica, la dirección en la que actúa, el lugar de aplicación y la postura del cuerpo. [9] [10] : 350
El cuerpo humano es flexible y deformable, en particular los tejidos más blandos. Una bofetada fuerte en la cara puede imponer brevemente cientos de g a nivel local, pero no producir ningún daño real; sin embargo, una fuerza g constante de 16 g durante un minuto puede ser mortal. Cuando se experimenta vibración , los niveles de fuerza g pico relativamente bajos pueden ser muy dañinos si se encuentran en la frecuencia de resonancia de los órganos o los tejidos conectivos. [ cita requerida ]
Hasta cierto punto, la tolerancia a la gravedad puede entrenarse, y también existe una variación considerable en la capacidad innata entre individuos. Además, algunas enfermedades, en particular los problemas cardiovasculares , reducen la tolerancia a la gravedad.
Los pilotos de aviones (en particular) soportan fuerzas g a lo largo del eje alineado con la columna vertebral. Esto provoca una variación significativa en la presión arterial a lo largo del cuerpo del sujeto, lo que limita las fuerzas g máximas que pueden tolerar.
La fuerza g positiva, o "ascendente", impulsa la sangre hacia abajo, a los pies de una persona sentada o de pie (de manera más natural, los pies y el cuerpo pueden verse como impulsados por la fuerza ascendente del piso y el asiento, hacia arriba alrededor de la sangre). La resistencia a la fuerza g positiva varía. Una persona típica puede soportar alrededor de 5 g 0 (49 m/s 2 ) (lo que significa que algunas personas pueden desmayarse al montar en una montaña rusa de mayor g, que en algunos casos excede este punto) antes de perder el conocimiento , pero a través de la combinación de trajes g especiales y esfuerzos para tensar los músculos, que actúan para forzar la sangre de regreso al cerebro, los pilotos modernos generalmente pueden soportar una fuerza sostenida de 9 g 0 (88 m/s 2 ) (ver Entrenamiento de alta G ).
En particular, en los aviones, las fuerzas g verticales suelen ser positivas (hacen que la sangre se dirija hacia los pies y se aleje de la cabeza), lo que provoca problemas en los ojos y el cerebro en particular. A medida que aumenta progresivamente la fuerza g vertical positiva (como en una centrífuga ), pueden experimentarse los siguientes síntomas: [ cita requerida ]
La resistencia a la fuerza g "negativa" o "hacia abajo", que impulsa la sangre a la cabeza, es mucho menor. Este límite se encuentra típicamente en el rango de -2 a -3 g 0 (-20 a -29 m/s 2 ). Esta condición a veces se conoce como " enrojecimiento" , donde la visión está literalmente enrojecida [12] debido a que el párpado inferior cargado de sangre es empujado hacia el campo visual. [13] La fuerza g negativa generalmente es desagradable y puede causar daños. Los vasos sanguíneos en los ojos o el cerebro pueden hincharse o estallar debido al aumento de la presión arterial, lo que resulta en una visión degradada o incluso ceguera.
El cuerpo humano resiste mejor las fuerzas g perpendiculares a la columna vertebral. En general, cuando la aceleración es hacia delante (el sujeto está básicamente acostado boca arriba, coloquialmente conocido como "ojos hacia adentro"), [14] se muestra una tolerancia mucho mayor que cuando la aceleración es hacia atrás (acostado boca abajo, "ojos hacia afuera"), ya que los vasos sanguíneos de la retina parecen más sensibles en esta última dirección. [ cita requerida ]
Los primeros experimentos demostraron que los humanos no entrenados podían tolerar una variedad de aceleraciones dependiendo del tiempo de exposición. Esto variaba desde hasta20 g 0 durante menos de 10 segundos, a10 g 0 durante 1 minuto, y6 g 0 durante 10 minutos para ambos globos oculares dentro y fuera. [15] Estas fuerzas se soportaron con las capacidades cognitivas intactas, ya que los sujetos pudieron realizar tareas físicas y de comunicación simples. Se determinó que las pruebas no causaron daño a largo o corto plazo, aunque la tolerancia fue bastante subjetiva, y solo los no pilotos más motivados fueron capaces de completar las pruebas. [16] El récord de tolerancia experimental máxima a la fuerza g horizontal lo tiene el pionero de la aceleración John Stapp , en una serie de experimentos de desaceleración de trineo cohete que culminaron en una prueba a fines de 1954 en la que se registró un poco más de un segundo desde una velocidad terrestre de Mach 0,9. Sobrevivió a una aceleración máxima "con los ojos fuera" de 46,2 veces la aceleración de la gravedad y más de25 g 0 durante 1,1 segundos, lo que demuestra que el cuerpo humano es capaz de hacer esto. Stapp vivió otros 45 años hasta los 89 [17] sin sufrir efectos nocivos. [18]
La fuerza g más alta registrada experimentada por un humano que sobrevivió fue durante la final de la IndyCar Series de 2003 en el Texas Motor Speedway el 12 de octubre de 2003, en la Chevy 500 de 2003, cuando el automóvil conducido por Kenny Bräck hizo un contacto de rueda con rueda con el automóvil de Tomas Scheckter . Esto provocó inmediatamente que el automóvil de Bräck impactara contra la valla de contención, lo que registraría un pico de fuerza g.214 g 0 . [19] [20]
Los términos impacto y choque mecánico se utilizan generalmente para describir una excitación de corta duración y alta energía cinética . Un pulso de choque se mide a menudo por su aceleración máxima en ɡ 0 ·s y la duración del pulso. La vibración es una oscilación periódica que también se puede medir en ɡ 0 ·s y en frecuencia. La dinámica de estos fenómenos es lo que los distingue de las fuerzas g causadas por aceleraciones de duración relativamente más larga. [ cita requerida ]
Después de una caída libre desde una altura seguida de una desaceleración a lo largo de una distancia durante un impacto, el impacto sobre un objeto es · ɡ 0 . Por ejemplo, un objeto rígido y compacto que se deja caer desde 1 m y que impacta a una distancia de 1 mm se ve sometido a una desaceleración de 1000 ɡ 0 . [ cita requerida ]
El tirón es la tasa de cambio de la aceleración. En unidades del SI, el tirón se expresa en m/s 3 ; también se puede expresar en gravedad estándar por segundo ( ɡ 0 /s; 1 ɡ 0 /s ≈ 9,81 m/s 3 ). [ cita requerida ]
Una investigación reciente realizada sobre extremófilos en Japón involucró una variedad de bacterias (incluyendo E. coli como control no extremófilo) que se sometieron a condiciones de gravedad extrema. Las bacterias se cultivaron mientras rotaban en una ultracentrífuga a altas velocidades correspondientes a 403.627 g. Paracoccus denitrificans fue una de las bacterias que mostró no solo supervivencia sino también un crecimiento celular robusto en estas condiciones de hiperaceleración, que generalmente solo se encuentran en entornos cósmicos, como en estrellas muy masivas o en las ondas de choque de las supernovas . El análisis mostró que el pequeño tamaño de las células procariotas es esencial para un crecimiento exitoso en hipergravedad . En particular, se demostró que dos especies multicelulares, los nematodos Panagrolaimus superbus [21] y Caenorhabditis elegans , pueden tolerar 400.000 × g durante 1 hora. [22] La investigación tiene implicaciones en la viabilidad de la panspermia . [23] [24]

Un acelerómetro , en su forma más simple, es una masa amortiguada en el extremo de un resorte, con alguna forma de medir qué tan lejos se ha movido la masa en el resorte en una dirección particular, llamada "eje".
Los acelerómetros suelen calibrarse para medir la fuerza g a lo largo de uno o más ejes. Si un acelerómetro estacionario de un solo eje se orienta de modo que su eje de medición sea horizontal, su salida será 0 g y seguirá siendo 0 g si se monta en un automóvil que viaja a una velocidad constante en una carretera nivelada. Cuando el conductor presiona el pedal del freno o del acelerador, el acelerómetro registrará una aceleración positiva o negativa.
Si el acelerómetro se gira 90° para que quede en posición vertical, la lectura será de +1 g hacia arriba, aunque esté parado. En esa situación, el acelerómetro está sujeto a dos fuerzas: la fuerza gravitatoria y la fuerza de reacción del suelo sobre la que se apoya. El acelerómetro solo puede medir esta última fuerza, debido a la interacción mecánica entre el acelerómetro y el suelo. La lectura es la aceleración que tendría el instrumento si estuviera sujeto exclusivamente a esa fuerza.
Un acelerómetro de tres ejes emitirá una gravedad cero en los tres ejes si se lo deja caer o se lo coloca de alguna otra manera en una trayectoria balística (también conocida como trayectoria inercial ), de modo que experimente una "caída libre", como lo hacen los astronautas en órbita (los astronautas experimentan pequeñas aceleraciones de marea llamadas microgravedad, que se descuidan a los efectos de la discusión aquí). Algunas atracciones de parques de diversiones pueden proporcionar varios segundos a una gravedad cercana a cero. Viajar en el " Vomit Comet " de la NASA proporciona una fuerza g cercana a cero durante unos 25 segundos seguidos.
{{cite web}}: CS1 maint: nombres numéricos: lista de autores ( enlace ){{cite journal}}: CS1 maint: varios nombres: lista de autores ( enlace ){{cite web}}: CS1 maint: bot: estado de URL original desconocido ( enlace )