En ingeniería de transporte , el flujo de tráfico es el estudio de las interacciones entre los viajeros (incluidos peatones, ciclistas, conductores y sus vehículos) y la infraestructura (incluidas las carreteras, la señalización y los dispositivos de control de tráfico), con el objetivo de comprender y desarrollar una red de transporte óptima con un movimiento eficiente del tráfico y problemas mínimos de congestión del tráfico .
Los fundamentos del análisis moderno del flujo de tráfico se remontan a la década de 1920, con el análisis del equilibrio del tráfico de Frank Knight , que fue desarrollado por Wardrop en 1952. A pesar de los avances en informática, sigue siendo difícil encontrar una teoría universalmente satisfactoria que se pueda aplicar a las condiciones del mundo real. Los modelos actuales combinan técnicas empíricas y teóricas para pronosticar el tráfico e identificar áreas de congestión, teniendo en cuenta variables como el uso de vehículos y los cambios en el terreno.
El flujo de tráfico se ve afectado por las interacciones complejas de los vehículos, que muestran comportamientos como la formación de grupos y la propagación de ondas de choque . Las variables clave del flujo de tráfico incluyen la velocidad, el flujo y la densidad, que están interconectadas. El tráfico fluido se caracteriza por menos de 12 vehículos por milla por carril, mientras que las densidades más altas pueden generar condiciones inestables y un tráfico persistente de paradas y arranques. Los modelos y diagramas, como los diagramas de tiempo-espacio, ayudan a visualizar y analizar estas dinámicas. El análisis del flujo de tráfico se puede abordar a diferentes escalas: microscópica (comportamiento de vehículos individuales), macroscópica (modelos similares a la dinámica de fluidos) y mesoscópica (funciones de probabilidad para distribuciones de vehículos). Los ingenieros suelen utilizar enfoques empíricos, como los descritos en el Manual de capacidad de carreteras , para modelar y pronosticar el flujo de tráfico, incorporando factores como el consumo de combustible y las emisiones.
El modelo de onda cinemática , introducido por Lighthill y Whitham en 1955, es una piedra angular de la teoría del flujo de tráfico, que describe la propagación de las ondas de tráfico y el impacto de los cuellos de botella. Los cuellos de botella, ya sean estacionarios o móviles, alteran significativamente el flujo y reducen la capacidad de la carretera. La Autoridad Federal de Carreteras atribuye el 40% de la congestión a los cuellos de botella. Las teorías clásicas del flujo de tráfico incluyen el modelo de Lighthill-Whitham-Richards y varios modelos de seguimiento de automóviles que describen cómo interactúan los vehículos en los flujos de tráfico. Una teoría alternativa, la teoría del tráfico trifásico de Kerner , sugiere una gama de capacidades en los cuellos de botella en lugar de un valor único. El modelo de fusión de Newell-Daganzo y los modelos de seguimiento de automóviles refinan aún más nuestra comprensión de la dinámica del tráfico y son fundamentales en la ingeniería y simulación de tráfico modernas.
Los intentos de producir una teoría matemática del flujo de tráfico se remontan a la década de 1920, cuando el economista estadounidense Frank Knight produjo por primera vez un análisis del equilibrio del tráfico, que se perfeccionó en el primer y segundo principio de equilibrio de Wardrop en 1952.
Sin embargo, incluso con la llegada de una importante capacidad de procesamiento informático, hasta la fecha no ha habido una teoría general satisfactoria que pueda aplicarse de manera consistente a las condiciones reales de flujo. Los modelos de tráfico actuales utilizan una combinación de técnicas empíricas y teóricas . Estos modelos se convierten luego en pronósticos de tráfico y tienen en cuenta los cambios locales o importantes propuestos, como el aumento del uso de vehículos, los cambios en el uso del suelo o los cambios en el modo de transporte (con la gente pasando del autobús al tren o al coche, por ejemplo), y para identificar áreas de congestión donde es necesario ajustar la red.

El tráfico se comporta de forma compleja y no lineal, dependiendo de las interacciones de un gran número de vehículos . Debido a las reacciones individuales de los conductores humanos, los vehículos no interactúan simplemente siguiendo las leyes de la mecánica, sino que muestran formación de grupos y propagación de ondas de choque , [ cita requerida ] tanto hacia adelante como hacia atrás, dependiendo de la densidad de vehículos . Algunos modelos matemáticos del flujo de tráfico utilizan un supuesto de cola vertical , en el que los vehículos a lo largo de un enlace congestionado no se desbordan a lo largo de la longitud del enlace.
En una red de flujo libre, la teoría del flujo de tráfico se refiere a las variables de flujo de tráfico de velocidad, flujo y concentración. Estas relaciones se refieren principalmente al flujo de tráfico ininterrumpido, que se encuentra principalmente en autopistas o vías rápidas. [1] Las condiciones de flujo se consideran "libres" cuando hay menos de 12 vehículos por milla por carril en una carretera. "Estable" a veces se describe como 12-30 vehículos por milla por carril. A medida que la densidad alcanza la tasa máxima de flujo másico (o flujo ) y excede la densidad óptima (por encima de 30 vehículos por milla por carril), el flujo de tráfico se vuelve inestable, e incluso un incidente menor puede dar lugar a condiciones de conducción de parada y arranque persistentes . Una condición de "avería" ocurre cuando el tráfico se vuelve inestable y excede los 67 vehículos por milla por carril. [2] La "densidad de atascos" se refiere a la densidad de tráfico extrema cuando el flujo de tráfico se detiene por completo, generalmente en el rango de 185-250 vehículos por milla por carril. [3]
Sin embargo, los cálculos sobre redes congestionadas son más complejos y se basan más en estudios empíricos y extrapolaciones de los recuentos de carreteras reales. Dado que estas suelen ser de naturaleza urbana o suburbana, otros factores (como la seguridad de los usuarios de la carretera y las consideraciones ambientales) también influyen en las condiciones óptimas.
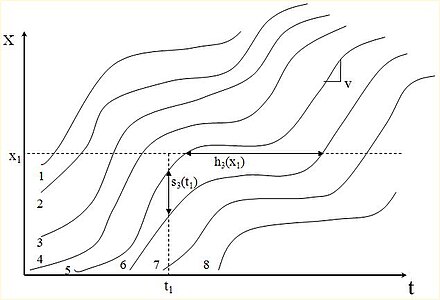
El flujo de tráfico generalmente está restringido a lo largo de una vía unidimensional (por ejemplo, un carril de circulación). Un diagrama de tiempo-espacio muestra gráficamente el flujo de vehículos a lo largo de una vía a lo largo del tiempo. El tiempo se muestra a lo largo del eje horizontal y la distancia se muestra a lo largo del eje vertical. El flujo de tráfico en un diagrama de tiempo-espacio se representa mediante las líneas de trayectoria individuales de los vehículos individuales. Los vehículos que se siguen entre sí a lo largo de un carril de circulación determinado tendrán trayectorias paralelas y las trayectorias se cruzarán cuando un vehículo pase a otro. Los diagramas de tiempo-espacio son herramientas útiles para mostrar y analizar las características del flujo de tráfico de un segmento de carretera determinado a lo largo del tiempo (por ejemplo, analizar la congestión del flujo de tráfico).
Hay tres variables principales para visualizar un flujo de tráfico: velocidad (v), densidad (indicada como k; el número de vehículos por unidad de espacio) y flujo [ aclaración necesaria ] (indicado como q; el número de vehículos por unidad de tiempo).
La velocidad es la distancia recorrida por unidad de tiempo. No se puede rastrear la velocidad de cada vehículo, por lo que, en la práctica, la velocidad promedio se mide mediante un muestreo de vehículos en un área determinada durante un período de tiempo. Se identifican dos definiciones de velocidad promedio: "velocidad media en el tiempo" y "velocidad media en el espacio".
donde m representa el número de vehículos que pasan por el punto fijo y v i es la velocidad del i- ésimo vehículo.
donde n representa el número de vehículos que pasan por el segmento de la carretera.
La "velocidad media espacial" es, por tanto, la media armónica de las velocidades. La velocidad media temporal nunca es menor que la velocidad media espacial: , donde es la varianza de la velocidad media espacial [4]

En un diagrama espacio-temporal, la velocidad instantánea, v = dx/dt, de un vehículo es igual a la pendiente de la trayectoria del vehículo. La velocidad media de un vehículo es igual a la pendiente de la línea que une los puntos finales de la trayectoria donde un vehículo entra y sale del segmento de la calzada. La separación vertical (distancia) entre trayectorias paralelas es la distancia entre vehículos (s) entre un vehículo líder y uno posterior. De manera similar, la separación horizontal (tiempo) representa la distancia entre vehículos (h). Un diagrama espacio-temporal es útil para relacionar la distancia entre vehículos y el flujo y la densidad del tráfico, respectivamente.
La densidad (k) se define como el número de vehículos por unidad de longitud de la calzada. En el flujo de tráfico, las dos densidades más importantes son la densidad crítica ( k c ) y la densidad de congestión ( k j ). La densidad máxima alcanzable en condiciones de flujo libre es k c , mientras que k j es la densidad máxima alcanzada en condiciones de congestión. En general, la densidad de congestión es cinco veces la densidad crítica. La inversa de la densidad es el espaciamiento (s), que es la distancia de centro a centro entre dos vehículos.


La densidad ( k ) dentro de una longitud de carretera ( L ) en un tiempo dado ( t1 ) es igual a la inversa del espaciamiento promedio de los n vehículos.
En un diagrama de tiempo-espacio, la densidad puede evaluarse en la región A.
donde tt es el tiempo total de viaje en A.

El flujo ( q ) es el número de vehículos que pasan por un punto de referencia por unidad de tiempo, vehículos por hora. El inverso del flujo es la distancia entre el vehículo i y el vehículo ( i + 1 ) que pasa por un punto de referencia en el espacio . En caso de congestión, h permanece constante. A medida que se forma un atasco, h tiende al infinito.
El flujo ( q ) que pasa por un punto fijo ( x1 ) durante un intervalo ( T ) es igual a la inversa de la distancia media entre los m vehículos.
En un diagrama de tiempo-espacio , el flujo puede evaluarse en la región B.
donde td es la distancia total recorrida en B.

Los analistas abordan el problema de tres maneras principales, correspondientes a las tres escalas principales de observación en física:
El enfoque de ingeniería para el análisis de los problemas de flujo de tráfico en las carreteras se basa principalmente en el análisis empírico (es decir, la observación y el ajuste matemático de curvas). Una de las principales referencias utilizadas por los planificadores estadounidenses es el Highway Capacity Manual [5] , publicado por el Transportation Research Board , que forma parte de la Academia Nacional de Ciencias de los Estados Unidos . Este recomienda modelar los flujos de tráfico utilizando todo el tiempo de viaje a través de un enlace utilizando una función de retardo/flujo, incluidos los efectos de las colas. Esta técnica se utiliza en muchos modelos de tráfico de EE. UU. y en el modelo SATURN en Europa. [6]
En muchas partes de Europa, se utiliza un enfoque empírico híbrido para el diseño del tráfico, que combina características macro, micro y mesoscópicas. En lugar de simular un estado estable de flujo para un viaje, se simulan "picos de demanda" transitorios de congestión. Estos se modelan utilizando pequeños "fragmentos de tiempo" en toda la red a lo largo de la jornada laboral o el fin de semana. Por lo general, primero se estiman los orígenes y destinos de los viajes y se genera un modelo de tráfico antes de calibrarlo comparando el modelo matemático con los recuentos observados de flujos de tráfico reales, clasificados por tipo de vehículo. Luego se aplica una "estimación matricial" al modelo para lograr una mejor coincidencia con los recuentos de enlaces observados antes de cualquier cambio, y el modelo revisado se utiliza para generar un pronóstico de tráfico más realista para cualquier esquema propuesto. El modelo se ejecutaría varias veces (incluida una línea base actual, un pronóstico de "día promedio" basado en una serie de parámetros económicos y respaldado por un análisis de sensibilidad) para comprender las implicaciones de bloqueos temporales o incidentes en la red. A partir de los modelos es posible totalizar el tiempo que tardan todos los conductores de diferentes tipos de vehículos en la red y deducir así el consumo medio de combustible y las emisiones.
Gran parte de la práctica de las autoridades del Reino Unido, Escandinavia y los Países Bajos consiste en utilizar el programa de modelado CONTRAM para grandes proyectos, que se ha desarrollado durante varias décadas bajo los auspicios del Laboratorio de Investigación de Transporte del Reino Unido y, más recientemente, con el apoyo de la Administración de Carreteras de Suecia . [7] Al modelar las previsiones de la red de carreteras para varias décadas en el futuro, se pueden calcular los beneficios económicos de los cambios en la red de carreteras, utilizando estimaciones del valor del tiempo y otros parámetros. El resultado de estos modelos se puede incorporar a un programa de análisis de costes y beneficios. [8]
Una curva de recuento de vehículos acumulativo, la curva N , muestra el número acumulado de vehículos que pasan por una determinada ubicación x en el tiempo t , medido a partir del paso de algún vehículo de referencia. [9] Esta curva se puede trazar si se conocen los tiempos de llegada de los vehículos individuales que se aproximan a una ubicación x , y también se conocen los tiempos de salida a medida que salen de la ubicación x . La obtención de estos tiempos de llegada y salida podría implicar la recopilación de datos: por ejemplo, se podrían establecer dos sensores puntuales en las ubicaciones X 1 y X 2 , y contar el número de vehículos que pasan por este segmento mientras se registra también el tiempo en que cada vehículo llega a X 1 y sale de X 2 . El gráfico resultante es un par de curvas acumulativas donde el eje vertical ( N ) representa el número acumulado de vehículos que pasan por los dos puntos: X 1 y X 2 , y el eje horizontal ( t ) representa el tiempo transcurrido desde X 1 y X 2 .


Si los vehículos no experimentan demoras mientras viajan de X 1 a X 2 , entonces las llegadas de vehículos a la ubicación X 1 están representadas por la curva N 1 y las llegadas de vehículos a la ubicación X 2 están representadas por N 2 en la figura 8. Más comúnmente, la curva N 1 se conoce como la curva de llegada de vehículos a la ubicación X 1 y la curva N 2 se conoce como la curva de llegada de vehículos a la ubicación X 2 . Usando un acceso señalizado de un carril a una intersección como ejemplo, donde X 1 es la ubicación de la barra de parada en el acceso y X 2 es una línea arbitraria en el carril de recepción justo al otro lado de la intersección, cuando el semáforo está en verde, los vehículos pueden viajar a través de ambos puntos sin demora y el tiempo que toma recorrer esa distancia es igual al tiempo de viaje de flujo libre. Gráficamente, esto se muestra como las dos curvas separadas en la figura 8.
Sin embargo, cuando el semáforo está en rojo, los vehículos llegan a la barra de parada ( X 1 ) y se demoran por la luz roja antes de cruzar X 2 algún tiempo después de que el semáforo se vuelva verde. Como resultado, se forma una cola en la barra de parada a medida que llegan más vehículos a la intersección mientras el semáforo aún está en rojo. Por lo tanto, mientras los vehículos que llegan a la intersección aún se ven obstaculizados por la cola, la curva N 2 ya no representa la llegada de los vehículos a la ubicación X 2 ; ahora representa la llegada virtual de los vehículos a la ubicación X 2 , o en otras palabras, representa la llegada de los vehículos a X 2 si no experimentaran ningún retraso. La llegada de los vehículos a la ubicación X 2 , teniendo en cuenta el retraso del semáforo, ahora está representada por la curva N′ 2 en la figura 9.
Sin embargo, el concepto de la curva de llegada virtual es erróneo. Esta curva no muestra correctamente la longitud de la cola resultante de la interrupción del tráfico (es decir, la señal roja). Supone que todos los vehículos siguen llegando a la barra de parada antes de que la luz roja los detenga. En otras palabras, la curva de llegada virtual representa la acumulación de vehículos verticalmente en la barra de parada. Cuando la señal de tráfico se pone verde, estos vehículos son atendidos en un orden de entrada-salida (FIFO). Sin embargo, para un enfoque de varios carriles, el orden de servicio no es necesariamente FIFO. No obstante, la interpretación sigue siendo útil debido a la preocupación por la demora total promedio en lugar de las demoras totales de los vehículos individuales. [10]

El ejemplo del semáforo muestra las curvas N como funciones suaves. Sin embargo, en teoría, al trazar curvas N a partir de los datos recopilados se debería obtener una función escalonada (figura 10). Cada escalón representa la llegada o salida de un vehículo en ese momento. [10] Cuando la curva N se dibuja a mayor escala y refleja un período de tiempo que abarca varios ciclos, se pueden ignorar los escalones de los vehículos individuales y la curva parecerá una función suave (figura 8).

El objetivo del análisis del flujo de tráfico es crear e implementar un modelo que permita a los vehículos llegar a su destino en el menor tiempo posible utilizando la máxima capacidad de la vía. Este proceso consta de cuatro pasos:
Este ciclo se repite hasta que la solución converja.
Hay dos enfoques principales para abordar este problema con los objetivos finales:
En resumen, una red está en estado óptimo del sistema (SO) cuando el costo total del sistema es el mínimo entre todas las asignaciones posibles.
El sistema óptimo se basa en el supuesto de que las rutas de todos los vehículos estarían controladas por el sistema, y que el redireccionamiento se basaría en la utilización máxima de los recursos y el costo total mínimo del sistema. (El costo puede interpretarse como el tiempo de viaje). Por lo tanto, en un algoritmo de enrutamiento óptimo del sistema, todas las rutas entre un par OD dado tienen el mismo costo marginal. En la economía del transporte tradicional, el sistema óptimo está determinado por el equilibrio de la función de demanda y la función de costo marginal. En este enfoque, el costo marginal se representa aproximadamente como una función creciente en la congestión del tráfico. En el enfoque del flujo de tráfico, el costo marginal del viaje puede expresarse como la suma del costo (tiempo de demora, w ) experimentado por el conductor y la externalidad ( e ) que un conductor impone al resto de los usuarios. [11]
Supongamos que hay una autopista (0) y una ruta alternativa (1), a la que los usuarios pueden desviarse hacia una rampa de salida. El operador conoce la tasa total de llegadas ( A ( t )), la capacidad de la autopista ( μ 0 ) y la capacidad de la ruta alternativa ( μ 1 ). Desde el momento 't 0 ', cuando la autopista está congestionada, algunos de los usuarios comienzan a moverse hacia la ruta alternativa. Sin embargo, cuando t 1 , la ruta alternativa también está llena de capacidad. Ahora el operador decide el número de vehículos (N) que utilizan la ruta alternativa. El número óptimo de vehículos ( N ) se puede obtener mediante el cálculo de la variación, para que el costo marginal de cada ruta sea igual. Por lo tanto, la condición óptima es T 0 = T 1 + ∆ 1 . En este gráfico, podemos ver que la cola en la ruta alternativa debe despejarse ∆ 1 unidades de tiempo antes de despejarse de la autopista. Esta solución no define cómo debemos asignar los vehículos que llegan entre t 1 y T 1 , solo podemos concluir que la solución óptima no es única. Si el operador desea que la autopista no esté congestionada, puede imponer el peaje por congestión, e 0 ― e 1 , que es la diferencia entre la externalidad de la autopista y la ruta alternativa. En esta situación, la autopista mantendrá la velocidad de flujo libre, sin embargo, la ruta alternativa estará extremadamente congestionada.
En resumen, una red está en equilibrio de usuario (UE) cuando cada conductor elige las rutas con menor costo entre el origen y el destino, independientemente de si se minimiza el costo total del sistema.
El equilibrio óptimo del usuario supone que todos los usuarios eligen su propia ruta hacia su destino en función del tiempo de viaje que se consumirá en diferentes opciones de ruta. Los usuarios elegirán la ruta que requiera el menor tiempo de viaje. El modelo óptimo del usuario se utiliza a menudo para simular el impacto en la asignación de tráfico por los cuellos de botella de la autopista. Cuando la congestión se produce en la autopista, extenderá el tiempo de demora en el viaje por la autopista y creará un tiempo de viaje más largo. Bajo el supuesto óptimo del usuario, los usuarios elegirían esperar hasta que el tiempo de viaje utilizando una determinada autopista sea igual al tiempo de viaje utilizando las calles de la ciudad y, por lo tanto, se alcance el equilibrio. Este equilibrio se llama equilibrio del usuario, equilibrio de Wardrop o equilibrio de Nash.

El principio básico del equilibrio del usuario es que todas las rutas utilizadas entre un par de OD determinado tienen el mismo tiempo de viaje. Se habilita una opción de ruta alternativa para su uso cuando el tiempo de viaje real en el sistema ha alcanzado el tiempo de viaje de flujo libre en esa ruta.
En la figura 15 se muestra un proceso típico de asignación de tráfico para un modelo óptimo de usuario de la autopista que considera una ruta alternativa. Cuando la demanda de tráfico se mantiene por debajo de la capacidad de la autopista, el tiempo de demora en la autopista permanece en cero. Cuando la demanda de tráfico excede la capacidad, aparecerá una cola de vehículos en la autopista y el tiempo de demora aumentará. Algunos usuarios se dirigirán a las calles de la ciudad cuando el tiempo de demora alcance la diferencia entre el tiempo de viaje de flujo libre en la autopista y el tiempo de viaje de flujo libre en las calles de la ciudad. Esto indica que los usuarios que permanecen en la autopista emplearán tanto tiempo de viaje como los que se desplacen hacia las calles de la ciudad. En esta etapa, el tiempo de viaje tanto en la autopista como en la ruta alternativa permanece igual. Esta situación puede terminar cuando la demanda cae por debajo de la capacidad de la carretera, es decir, el tiempo de viaje en la autopista comienza a disminuir y todos los usuarios permanecerán en la autopista. La suma del área de la parte 1 y 3 representa los beneficios de proporcionar una ruta alternativa. La suma del área 4 y el área 2 muestra el costo total de demora en el sistema, donde el área 4 es la demora total que ocurre en la carretera y el área 2 es la demora adicional al desviar el tráfico a las calles de la ciudad.
La función de navegación en Google Maps puede considerarse una aplicación industrial típica de asignación dinámica de tráfico basada en el equilibrio del usuario, ya que proporciona a cada usuario la opción de ruta con el menor costo (tiempo de viaje).
Tanto el óptimo del usuario como el óptimo del sistema se pueden subdividir en dos categorías en función del enfoque de retardo de tiempo adoptado para su solución:
El retraso predictivo supone que el usuario del sistema sabe exactamente cuánto tiempo durará el retraso más adelante. El retraso predictivo sabe cuándo se alcanzará un cierto nivel de congestión y cuándo el retraso de ese sistema será mayor que el de tomar el otro sistema, por lo que la decisión de cambiar de ruta se puede tomar a tiempo. En el diagrama de recuento de vehículos-tiempo, el retraso predictivo en el tiempo t es un segmento de línea horizontal en el lado derecho del tiempo t, entre la curva de llegada y la de salida, que se muestra en la Figura 16. La coordenada y correspondiente es el número n de vehículos que salen del sistema en el tiempo t.

El retraso reactivo se produce cuando el usuario no tiene conocimiento de las condiciones del tráfico que se avecinan. El usuario espera a experimentar el punto en el que se observa el retraso y la decisión de desviar la ruta es una reacción a esa experiencia en el momento. El retraso predictivo proporciona resultados significativamente mejores que el método de retraso reactivo. En el diagrama de recuento de vehículos-tiempo, el retraso predictivo en el tiempo t es un segmento de línea horizontal en el lado izquierdo del tiempo t, entre la curva de llegada y salida, que se muestra en la Figura 16. La coordenada y correspondiente es el número n de vehículos que ingresa al sistema en el tiempo t.
Este es un enfoque de futuro para eliminar las ondas de choque y aumentar la seguridad de los vehículos. El concepto se basa en el hecho de que el riesgo de accidente en una carretera aumenta con la diferencia de velocidad entre los vehículos que circulan por delante y por detrás. Los dos tipos de riesgo de colisión que se pueden reducir con la implementación de VSL son la colisión por alcance y la colisión por cambio de carril. Los límites de velocidad variables buscan homogeneizar la velocidad, lo que genera un flujo más constante. [12] Los investigadores han implementado diferentes enfoques para construir un algoritmo VSL adecuado.
Los límites de velocidad variables se suelen aplicar cuando los sensores situados a lo largo de la calzada detectan que la congestión o los fenómenos meteorológicos han superado los umbrales. El límite de velocidad de la calzada se reducirá entonces en incrementos de 5 mph mediante el uso de señales sobre la calzada (señales de mensajes dinámicos) controladas por el Departamento de Transporte. El objetivo de este proceso es aumentar la seguridad mediante la reducción de accidentes y evitar o posponer la aparición de congestiones en la calzada. El flujo de tráfico resultante ideal es más lento en general, pero con menos paradas y arranques, lo que da como resultado menos casos de colisiones traseras y de cambio de carril. El uso de VSL también emplea regularmente carriles laterales permitidos para el transporte solo en estados congestionados, que este proceso pretende combatir. La necesidad de un límite de velocidad variable se muestra en el diagrama de densidad de flujo a la derecha.

En esta figura ("Diagrama de flujo y velocidad para una vía típica"), el punto de la curva representa el movimiento óptimo del tráfico tanto en flujo como en velocidad. Sin embargo, más allá de este punto, la velocidad de desplazamiento alcanza rápidamente un umbral y comienza a disminuir rápidamente. Para reducir el riesgo potencial de esta rápida disminución de la velocidad, los límites de velocidad variables reducen la velocidad a un ritmo más gradual (incrementos de 5 mph), lo que permite que los conductores tengan más tiempo para prepararse y aclimatarse a la desaceleración debido a la congestión o el clima. El desarrollo de una velocidad de desplazamiento uniforme reduce la probabilidad de un comportamiento errático del conductor y, por lo tanto, de accidentes.
A través de datos históricos obtenidos en los sitios de VSL, se ha determinado que la implementación de esta práctica reduce el número de accidentes entre un 20 y un 30%. [12]
Además de las cuestiones de seguridad y eficiencia, los VSL también pueden aportar beneficios medioambientales, como una reducción de las emisiones, el ruido y el consumo de combustible. Esto se debe a que los vehículos consumen menos combustible cuando circulan a una velocidad constante, en lugar de en un estado de aceleración y desaceleración constantes como el que suele darse en condiciones de congestión. [13]
Una consideración importante en la capacidad vial se relaciona con el diseño de los cruces. Al permitir largos "secciones de zigzag" en carreteras con curvas suaves en intersecciones niveladas, los vehículos a menudo pueden moverse a través de carriles sin causar interferencias significativas al flujo. Sin embargo, esto es costoso y ocupa una gran cantidad de tierra, por lo que a menudo se utilizan otros patrones, particularmente en áreas urbanas o muy rurales. La mayoría de los modelos grandes utilizan simulaciones rudimentarias para las intersecciones, pero existen simulaciones por computadora para modelar conjuntos específicos de semáforos, rotondas y otros escenarios donde el flujo se interrumpe o se comparte con otros tipos de usuarios de la carretera o peatones. Un cruce bien diseñado puede permitir un flujo de tráfico significativamente mayor en un rango de densidades de tráfico durante el día. Al adaptar un modelo de este tipo a un "sistema de transporte inteligente", el tráfico puede enviarse en "paquetes" ininterrumpidos de vehículos a velocidades predeterminadas a través de una serie de semáforos en fases. El TRL del Reino Unido ha desarrollado programas de modelado de cruces para esquemas locales de pequeña escala que pueden tener en cuenta la geometría detallada y las líneas de visión; ARCADY para rotondas, PICADY para intersecciones prioritarias y OSCADY y TRANSYT para semáforos. Existen muchos otros paquetes de software de análisis de intersecciones [14], como Sidra , LinSig y Synchro.
El modelo de onda cinemática fue aplicado por primera vez al flujo de tráfico por Lighthill y Whitham en 1955. Su artículo de dos partes desarrolló primero la teoría de las ondas cinemáticas usando el movimiento del agua como ejemplo. En la segunda mitad, extendieron la teoría al tráfico en “vías arteriales congestionadas”. Este artículo se centró principalmente en desarrollar la idea de los “resaltos” del tráfico (aumentos del flujo) y sus efectos sobre la velocidad, especialmente a través de los cuellos de botella. [15]
Los autores comenzaron por analizar los enfoques previos de la teoría del flujo de tráfico. Señalan que en ese momento se habían realizado algunos trabajos experimentales, pero que “los enfoques teóricos sobre el tema [estaban] en sus inicios”. Un investigador en particular, John Glen Wardrop, se interesó principalmente por los métodos estadísticos de examen, como la velocidad media espacial, la velocidad media temporal y “el efecto del aumento del flujo en los adelantamientos” y la consiguiente disminución de la velocidad que causaría. Otras investigaciones anteriores se habían centrado en dos modelos separados: uno relacionaba la velocidad del tráfico con el flujo de tráfico y otro relacionaba la velocidad con la distancia entre vehículos. [15]
El objetivo de Lighthill y Whitham, por otra parte, era proponer un nuevo método de estudio “sugerido por las teorías del flujo sobre proyectiles supersónicos y del movimiento de las inundaciones en los ríos”. El modelo resultante capturaría ambas relaciones antes mencionadas, velocidad-flujo y velocidad-intervalo, en una única curva, que “[resumiría] todas las propiedades de un tramo de carretera que son relevantes para su capacidad de manejar el flujo de tráfico congestionado”. El modelo que presentaron relacionaba el flujo de tráfico con la concentración (ahora conocida típicamente como densidad). Escribieron: “La hipótesis fundamental de la teoría es que en cualquier punto de la carretera el flujo q (vehículos por hora) es una función de la concentración k (vehículos por milla)”. Según este modelo, el flujo de tráfico se parecía al flujo de agua en que “los cambios leves en el flujo se propagan de vuelta a través de la corriente de vehículos a lo largo de 'ondas cinemáticas', cuya velocidad relativa a la carretera es la pendiente del gráfico del flujo en función de la concentración”. Los autores incluyeron un ejemplo de dicho gráfico; Este gráfico de flujo versus concentración (densidad) todavía se utiliza hoy en día (ver figura 3 arriba). [15]
Los autores utilizaron este modelo de concentración de flujo para ilustrar el concepto de ondas de choque, que frenan a los vehículos que entran en ellas, y las condiciones que las rodean. También analizaron los cuellos de botella y las intersecciones, ambos relacionados con su nuevo modelo. Para cada uno de estos temas, se incluyeron diagramas de concentración de flujo y de tiempo-espacio. Por último, los autores señalaron que no existía una definición consensuada de capacidad y argumentaron que debería definirse como el “flujo máximo del que es capaz la carretera”. Lighthill y Whitham también reconocieron que su modelo tenía una limitación importante: solo era apropiado para su uso en carreteras largas y concurridas, ya que el enfoque de “flujo continuo” solo funciona con una gran cantidad de vehículos. [15]
El modelo de onda cinemática de la teoría del flujo de tráfico es el modelo de flujo de tráfico dinámico más simple que reproduce la propagación de las ondas de tráfico . Está formado por tres componentes: el diagrama fundamental , la ecuación de conservación y las condiciones iniciales. La ley de conservación es la ley fundamental que rige el modelo de onda cinemática:
El diagrama fundamental del modelo de onda cinemática relaciona el flujo de tráfico con la densidad, como se ve en la figura 3 anterior. Puede escribirse como:
Finalmente, se deben definir las condiciones iniciales para resolver un problema utilizando el modelo. Un límite se define como , que representa la densidad como una función del tiempo y la posición. Estos límites suelen adoptar dos formas diferentes, lo que da como resultado problemas de valor inicial (IVP) y problemas de valor límite (BVP). Los problemas de valor inicial dan la densidad de tráfico en el momento , de modo que , donde es la función de densidad dada. Los problemas de valor límite dan una función que representa la densidad en la posición, de modo que . El modelo tiene muchos usos en el flujo de tráfico. Uno de los usos principales es el modelado de cuellos de botella de tráfico, como se describe en la siguiente sección.
Los cuellos de botella son interrupciones del tráfico en una vía causadas por el diseño de la vía, los semáforos o los accidentes. Hay dos tipos generales de cuellos de botella: fijos y móviles. Los cuellos de botella fijos son aquellos que surgen debido a una perturbación que se produce debido a una situación fija, como el estrechamiento de una vía o un accidente. Los cuellos de botella móviles, por otro lado, son aquellos vehículos o el comportamiento de los vehículos que causan la interrupción en los vehículos que están delante del vehículo. Por lo general, los cuellos de botella móviles son causados por camiones pesados, ya que son vehículos de movimiento lento con menos aceleración y también pueden cambiar de carril.7
Causas de la congestión del tráfico en Estados Unidos
Los cuellos de botella son factores importantes porque afectan el flujo del tráfico y la velocidad media de los vehículos. La consecuencia principal de un cuello de botella es una reducción inmediata de la capacidad de la carretera. La Autoridad Federal de Carreteras ha declarado que el 40% de toda la congestión se debe a cuellos de botella. [ cita requerida ]

La causa general de los cuellos de botella estacionarios son las pérdidas de carriles, que se producen cuando una carretera de varios carriles pierde uno o más de sus carriles. Esto hace que el tráfico vehicular en los carriles finales se incorpore a los otros carriles.
Como se explicó anteriormente, los cuellos de botella en movimiento se deben a vehículos que se mueven lentamente y causan interrupciones en el tráfico. Los cuellos de botella en movimiento pueden ser cuellos de botella activos o inactivos. Si la capacidad reducida (q u ) causada por un cuello de botella en movimiento es mayor que la capacidad real (μ) aguas abajo del vehículo, entonces se dice que este cuello de botella es un cuello de botella activo.
Los fundamentos y metodologías clásicas generalmente aceptados de la teoría del tráfico y el transporte son los siguientes:
La teoría del tráfico trifásico es una teoría alternativa del flujo de tráfico creada por Boris Kerner a finales de los años 1990 [24] [25] [26] (para ver reseñas, véanse los libros [27] [28] [29] ). Probablemente el resultado más importante de la teoría trifásica es que en cualquier instante de tiempo existe un rango de capacidades de la autopista de flujo libre en un cuello de botella. El rango de capacidad está entre algunas capacidades máximas y mínimas. El rango de capacidades de la autopista de flujo libre en el cuello de botella en la teoría del tráfico trifásico contradice fundamentalmente las teorías clásicas del tráfico, así como los métodos de gestión y control del tráfico que en cualquier instante de tiempo suponen la existencia de una capacidad de la autopista de flujo libre determinista o estocástica particular en el cuello de botella. Los no especialistas que nunca han aprendido sobre fenómenos de tráfico antes pueden encontrar explicaciones simplificadas de fenómenos de tráfico de vehículos medidos reales que conducen al surgimiento de la teoría del tráfico trifásico de Kerner en el libro; [30] algunas aplicaciones de ingeniería de la teoría de Kerner se pueden encontrar en el libro. [31]

En la condición de flujos de tráfico que salen de dos ramales de carreteras y se fusionan en un solo flujo a través de una sola carretera, determinar los flujos que pasan por el proceso de fusión y el estado de cada ramal de carreteras se convierte en una tarea importante para los ingenieros de tráfico. El modelo de fusión de Newell-Daganzo es un buen enfoque para resolver estos problemas. Este modelo simple es el resultado del resultado de la descripción de Gordon Newell del proceso de fusión [32] y del modelo de transmisión de celda de Daganzo . [33] Para aplicar el modelo para determinar los flujos que salen de dos ramales de carreteras y el estado de cada ramal de carreteras, es necesario conocer las capacidades de los dos ramales de entrada de las carreteras, la capacidad de salida, las demandas de cada ramal de carreteras y el número de carriles de la carretera única. La relación de fusión se calculará para determinar la proporción de los dos flujos de entrada cuando ambos ramales de la carretera están operando en condiciones de congestión.
Como se puede ver en un modelo simplificado del proceso de fusión, [34] la capacidad de salida del sistema se define como μ, las capacidades de las dos ramas de entrada de las carreteras se definen como μ 1 y μ 2 , y las demandas para cada rama de las carreteras se definen como q 1 D y q 2 D . Los q 1 y q 2 son la salida del modelo que son los flujos que pasan a través del proceso de fusión. El proceso del modelo se basa en el supuesto de que la suma de las capacidades de las dos ramas de entrada de las carreteras es menor que la capacidad de salida del sistema, μ 1 + μ 2 ≤ μ.
Los modelos de seguimiento de vehículos describen cómo un vehículo sigue a otro en un flujo de tráfico ininterrumpido. Son un tipo de modelo de flujo de tráfico microscópico .
Una encuesta sobre el estado del arte en el modelado del flujo de tráfico:
Libros útiles desde el punto de vista físico: