En ecología y economía de poblaciones , el rendimiento máximo sostenible ( RMS ) es teóricamente el mayor rendimiento (o captura) que se puede obtener de las existencias de una especie durante un período indefinido. Fundamental para la noción de cosecha sostenible , el concepto de RMS tiene como objetivo mantener el tamaño de la población en el punto de tasa de crecimiento máximo cosechando los individuos que normalmente se agregarían a la población, lo que permite que la población continúe siendo productiva indefinidamente. Bajo el supuesto de crecimiento logístico , la limitación de recursos no restringe las tasas de reproducción de los individuos cuando las poblaciones son pequeñas, pero debido a que hay pocos individuos, el rendimiento general es pequeño. En densidades de población intermedias, también representadas por la mitad de la capacidad de carga , los individuos pueden reproducirse a su tasa máxima. En este punto, llamado rendimiento máximo sostenible, hay un excedente de individuos que se pueden cosechar porque el crecimiento de la población está en su punto máximo debido a la gran cantidad de individuos reproductores. Por encima de este punto, los factores dependientes de la densidad limitan cada vez más la reproducción hasta que la población alcanza la capacidad de carga. En este punto, no hay individuos excedentes para cosechar y el rendimiento cae a cero. El rendimiento máximo sostenible suele ser mayor que el rendimiento sostenible óptimo y el rendimiento económico máximo.
El RMS se utiliza ampliamente en la gestión pesquera . A diferencia del modelo logístico ( Schaefer ), [1] el RMS se ha perfeccionado en la mayoría de los modelos pesqueros modernos y se da en alrededor del 30% del tamaño de la población no explotada. [2] [3] Esta fracción difiere entre poblaciones dependiendo del ciclo de vida de la especie y la selectividad específica por edad del método de pesca.
El concepto de RMS como estrategia de gestión pesquera se desarrolló en Belmar , Nueva Jersey , a principios de la década de 1930. [4] [5] [6] Aumentó en popularidad en la década de 1950 con el advenimiento de los modelos de producción excedente con estimación explícita del RMS. [1] Como un objetivo de gestión aparentemente simple y lógico, combinado con la falta de otros objetivos de gestión simples de la época, el RMS fue adoptado como el objetivo de gestión principal por varias organizaciones internacionales (por ejemplo, IWC , IATTC , [7] ICCAT , ICNAF ) y países individuales. [8]
Entre 1949 y 1955, Estados Unidos maniobró para que se declarara el RMS como el objetivo de la ordenación pesquera internacional (Johnson 2007). El tratado internacional sobre el RMS que finalmente se adoptó en 1955 otorgó a las flotas extranjeras el derecho a pescar en cualquier costa. Las naciones que querían excluir a los barcos extranjeros primero tenían que demostrar que sus peces estaban sobreexplotados. [9]
A medida que se fue adquiriendo experiencia con el modelo, algunos investigadores se dieron cuenta de que carecía de la capacidad para abordar las complejidades operativas del mundo real y la influencia de las interacciones tróficas y de otro tipo. En 1977, Peter Larkin escribió su epitafio, cuestionando el objetivo del rendimiento máximo sostenido por varios motivos: ponía a las poblaciones en demasiado riesgo; no tenía en cuenta la variabilidad espacial de la productividad; no tenía en cuenta otras especies que no fueran el objetivo de la pesquería; sólo consideraba los beneficios, no los costos, de la pesca; y era sensible a la presión política. [10] De hecho, ninguna de estas críticas apuntaba a la sostenibilidad como objetivo. La primera señalaba que buscar el rendimiento máximo sostenible absoluto con parámetros inciertos era arriesgado. El resto señala que el objetivo del rendimiento máximo sostenible no era holístico; dejaba fuera demasiadas características relevantes. [9]
Algunos administradores comenzaron a utilizar recomendaciones de cuotas más conservadoras, pero la influencia del modelo de RMS para la gestión pesquera aún prevalecía. Incluso cuando la comunidad científica comenzaba a cuestionar la idoneidad y eficacia del RMS como objetivo de gestión, [10] [11] se incorporó a la Convención de las Naciones Unidas sobre el Derecho del Mar de 1982 , asegurando así su integración en las leyes y leyes pesqueras nacionales e internacionales. [8] Según Walters y Maguire, se había puesto en marcha un «gigante institucional», que alcanzó su clímax a principios de los años 1990 con el colapso del bacalao del norte . [12]
El supuesto clave detrás de todos los modelos de cosecha sustentable , como el MSY, es que las poblaciones de organismos crecen y se reemplazan a sí mismas, es decir, son recursos renovables. Además, se supone que, dado que las tasas de crecimiento, supervivencia y reproducción aumentan cuando la cosecha reduce la densidad de población [4] , producen un excedente de biomasa que se puede cosechar. De lo contrario, la cosecha sustentable no sería posible.
Otro supuesto de la recolección de recursos renovables es que las poblaciones de organismos no siguen creciendo indefinidamente; alcanzan un tamaño de población de equilibrio, que ocurre cuando el número de individuos coincide con los recursos disponibles para la población (es decir, supongamos que el crecimiento logístico clásico ). En este tamaño de población de equilibrio, llamado capacidad de carga , la población permanece en un tamaño estable. [13]
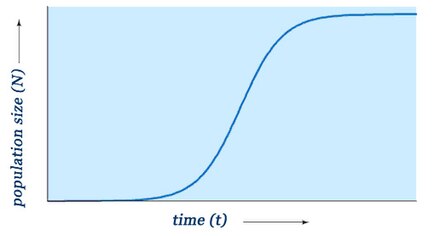
El modelo logístico (o función logística ) es una función que se utiliza para describir el crecimiento poblacional acotado bajo los dos supuestos anteriores. La función logística está acotada en ambos extremos: cuando no hay individuos para reproducirse y cuando hay un número de individuos en equilibrio (es decir, en la capacidad de carga ). Bajo el modelo logístico, la tasa de crecimiento poblacional entre estos dos límites se supone con mayor frecuencia como sigmoidea (Figura 1). Existe evidencia científica de que algunas poblaciones crecen de manera logística hacia un equilibrio estable; un ejemplo que se cita comúnmente es el crecimiento logístico de la levadura .
La ecuación que describe el crecimiento logístico es: [13]
Los valores de los parámetros son:
A partir de la función logística, se puede calcular el tamaño de la población en cualquier punto siempre que se conozcan , , y .

La ecuación diferencial 1.1 da una expresión que representa cómo aumenta la tasa de población a medida que N aumenta. Al principio, la tasa de crecimiento de la población es rápida, pero comienza a disminuir a medida que la población crece hasta que se estabiliza en la tasa de crecimiento máxima, después de lo cual comienza a disminuir (figura 2).
La ecuación de la figura 2 es la diferencial de la ecuación 1.1 ( modelo de crecimiento de Verhulst de 1838 ): [13]
puede entenderse como el cambio en la población (N) con respecto a un cambio en el tiempo (t). La ecuación 1.2 es la forma habitual en que se representa matemáticamente el crecimiento logístico y tiene varias características importantes. Primero, en tamaños de población muy bajos, el valor de es pequeño, por lo que la tasa de crecimiento de la población es aproximadamente igual a , lo que significa que la población está creciendo exponencialmente a una tasa r (la tasa intrínseca de aumento de la población). A pesar de esto, la tasa de crecimiento de la población es muy baja (valores bajos en el eje y de la figura 2) porque, aunque cada individuo se reproduce a una tasa alta, hay pocos individuos reproductores presentes. Por el contrario, cuando la población es grande, el valor de se acerca a 1, lo que reduce efectivamente los términos dentro de los corchetes de la ecuación 1.2 a cero. El efecto es que la tasa de crecimiento de la población es nuevamente muy baja, porque cada individuo apenas se reproduce o las tasas de mortalidad son altas. [13] Como resultado de estos dos extremos, la tasa de crecimiento de la población es máxima en una población intermedia o la mitad de la capacidad de carga ( ).

La forma más sencilla de modelar la cosecha es modificar la ecuación logística de modo que se elimine continuamente una cierta cantidad de individuos: [13]
Donde H representa el número de individuos que se eliminan de la población, es decir, la tasa de cosecha. Cuando H es constante, la población estará en equilibrio cuando el número de individuos que se eliminan sea igual a la tasa de crecimiento de la población (figura 3). El tamaño de la población en equilibrio bajo un régimen de cosecha particular se puede encontrar cuando la población no está creciendo, es decir, cuando . Esto ocurre cuando la tasa de crecimiento de la población es la misma que la tasa de cosecha:
La figura 3 muestra cómo varía la tasa de crecimiento con la densidad de población. En densidades bajas (lejos de la capacidad de sustentación), hay poca adición (o "reclutamiento") a la población, simplemente porque hay pocos organismos que den a luz. Sin embargo, en densidades altas, hay una intensa competencia por los recursos y la tasa de crecimiento es nuevamente baja porque la tasa de mortalidad es alta. Entre estos dos extremos, la tasa de crecimiento de la población aumenta hasta un valor máximo ( ). Este punto máximo representa el número máximo de individuos que se pueden agregar a una población mediante procesos naturales. Si se eliminan más individuos de la población, la población corre el riesgo de disminuir hasta extinguirse. [14] El número máximo que se puede cosechar de manera sostenible, llamado rendimiento máximo sostenible, está dado por este punto máximo.
La figura 3 también muestra varios valores posibles para la tasa de cosecha, H. En , hay dos posibles puntos de equilibrio de la población: un tamaño de población bajo ( ) y uno alto ( ). En , una tasa de cosecha ligeramente más alta, sin embargo, solo hay un punto de equilibrio (en ), que es el tamaño de la población que produce la tasa de crecimiento máxima. Con el crecimiento logístico, este punto, llamado rendimiento máximo sostenible, es donde el tamaño de la población es la mitad de la capacidad de carga (o ). El rendimiento máximo sostenible es el mayor rendimiento que se puede obtener de una población en equilibrio. En la figura 3, si es mayor que , la cosecha excedería la capacidad de la población para reemplazarse a sí misma en cualquier tamaño de población ( en la figura 3). Debido a que la tasa de cosecha es mayor que la tasa de crecimiento de la población en todos los valores de , esta tasa de cosecha no es sostenible.
Una característica importante del modelo MSY es cómo las poblaciones cosechadas responden a las fluctuaciones ambientales o la extracción ilegal. Considere una población en cosechada a un nivel de cosecha constante . Si la población cae (debido a un mal invierno o una cosecha ilegal) esto facilitará la regulación de la población dependiente de la densidad y aumentará el rendimiento, moviendo la población de nuevo a , un equilibrio estable. En este caso, un bucle de retroalimentación negativa crea estabilidad. Sin embargo, el punto de equilibrio inferior para el nivel de cosecha constante no es estable; un colapso de la población o la cosecha ilegal reducirá el rendimiento de la población aún más por debajo del nivel de cosecha actual, creando un bucle de retroalimentación positiva que conduce a la extinción. La cosecha en también es potencialmente inestable. Una pequeña disminución en la población puede conducir a un bucle de retroalimentación positiva y la extinción si el régimen de cosecha ( ) no se reduce. Por lo tanto, algunos consideran que la cosecha en MSY es insegura por razones ecológicas y económicas. [14] [15] El modelo MSY en sí puede modificarse para cosechar un cierto porcentaje de la población o con restricciones de esfuerzo constantes en lugar de un número real, evitando así algunas de sus inestabilidades. [14]
El punto de equilibrio del RMS es semiestable: se compensa un pequeño aumento del tamaño de la población, y una pequeña disminución conduce a la extinción si no se reduce H. Por lo tanto, la recolección en el RMS es peligrosa porque se encuentra en el filo de una navaja: cualquier pequeña disminución de la población conduce a una retroalimentación positiva, y la población disminuye rápidamente hasta la extinción si el número de cosechados se mantiene igual. [14] [15]
La fórmula para la cosecha máxima sostenida ( ) es un cuarto de la población máxima o capacidad de carga ( ) multiplicada por la tasa intrínseca de crecimiento ( ). [16]
El principio de RMS a menudo también se aplica a poblaciones estructuradas por edad. [17] Los cálculos pueden ser más complicados y los resultados a menudo dependen de si la dependencia de la densidad ocurre en la etapa larvaria (a menudo modelada como reproducción dependiente de la densidad) y/o en otras etapas de la vida. [18] Se ha demostrado que si la dependencia de la densidad solo actúa en la larva, entonces existe una etapa de vida óptima (tamaño o clase de edad) para cosechar, sin cosecha de todas las demás etapas de la vida. [17] Por lo tanto, la estrategia óptima es cosechar esta etapa de vida más valiosa en RMS. [19] Sin embargo, en los modelos estructurados por edad y etapa, no siempre existe un RMS constante. En tales casos, la cosecha cíclica es óptima cuando el rendimiento y el recurso fluctúan en tamaño, a través del tiempo. [20] Además, la estocasticidad ambiental interactúa con las poblaciones demográficamente estructuradas de formas fundamentalmente diferentes que para las poblaciones no estructuradas al determinar la cosecha óptima. De hecho, la biomasa óptima que debe quedar en el océano, cuando se pesca al RMS, puede ser mayor o menor que en modelos deterministas análogos, dependiendo de los detalles de la función de reclutamiento dependiente de la densidad, si la estructura de etapas también se incluye en el modelo. [21]
Comenzar a cosechar una población que no se había cosechado antes siempre conducirá a una disminución del tamaño de la población. Es decir, es imposible que una población cosechada se mantenga en su capacidad de carga original. En cambio, la población se estabilizará en un nuevo tamaño de equilibrio más bajo o, si la tasa de cosecha es demasiado alta, disminuirá a cero.
La razón por la que las poblaciones pueden ser cosechadas de manera sostenible es que exhiben una respuesta dependiente de la densidad. [14] [15] Esto significa que, a cualquier tamaño de población por debajo de K, la población está produciendo un excedente de rendimiento que está disponible para cosechar sin reducir el tamaño de la población. La dependencia de la densidad es el proceso regulador que permite que la población regrese al equilibrio después de una perturbación. La ecuación logística supone que la dependencia de la densidad toma la forma de retroalimentación negativa. [15]
Si se extrae una cantidad constante de individuos de una población a un nivel superior al RMS, la población disminuirá hasta extinguirse. La extracción por debajo del nivel RMS conduce a una población de equilibrio estable si la población inicial es superior al tamaño de la población de equilibrio inestable.
El rendimiento máximo sostenible ha sido especialmente influyente en la gestión de los recursos biológicos renovables, como los peces y la fauna silvestre de importancia comercial. En términos pesqueros, el rendimiento máximo sostenible (RMS) es la mayor captura media que se puede obtener de una población en las condiciones ambientales existentes. [22] El RMS apunta a un equilibrio entre una captura excesiva y una captura insuficiente para mantener la población en una abundancia intermedia con una tasa de reemplazo máxima.
En relación con el RMS, el rendimiento económico máximo (REM) es el nivel de captura que proporciona los máximos beneficios o ganancias económicas netas a la sociedad. [23] [24] Al igual que el rendimiento sostenible óptimo , el REM suele ser menor que el RMS.
Aunque es una práctica muy extendida por las agencias gubernamentales estatales y federales que regulan la vida silvestre, los bosques y la pesca, el rendimiento máximo sostenible ha sido objeto de fuertes críticas por parte de los ecologistas y otros, tanto por razones teóricas como prácticas. [15] El concepto de rendimiento máximo sostenible no siempre es fácil de aplicar en la práctica. Los problemas de estimación surgen debido a suposiciones deficientes en algunos modelos y a la falta de fiabilidad de los datos. [8] [25] Los biólogos, por ejemplo, no siempre tienen suficientes datos para determinar con claridad el tamaño y la tasa de crecimiento de la población. Calcular el punto en el que una población comienza a disminuir debido a la competencia también es muy difícil. El concepto de rendimiento máximo sostenible también tiende a tratar a todos los individuos de la población como idénticos, ignorando así todos los aspectos de la estructura de la población, como el tamaño o las clases de edad y sus tasas diferenciales de crecimiento, supervivencia y reproducción. [25]
Como objetivo de gestión, la interpretación estática del RMS (es decir, el RMS como una captura fija que puede realizarse año tras año) generalmente no es apropiada porque ignora el hecho de que las poblaciones de peces experimentan fluctuaciones naturales (es decir, el RMS trata al medio ambiente como invariable) en abundancia y, por lo general, en última instancia se agotarán gravemente con una estrategia de captura constante. [25] Por lo tanto, la mayoría de los científicos pesqueros interpretan ahora el RMS en un sentido más dinámico como el rendimiento promedio máximo (PME) obtenido al aplicar una estrategia de cosecha específica a un recurso fluctuante. [8] O como una "estrategia de escape" óptima, donde escape significa la cantidad de peces que debe permanecer en el océano [en lugar de la cantidad de peces que se pueden cosechar]. Una estrategia de escape es a menudo la estrategia óptima para maximizar el rendimiento esperado de una población cosechada que fluctúa estocásticamente. [26]
Sin embargo, las limitaciones del RMS no significan que su rendimiento sea peor que el de los humanos que utilizan su mejor criterio intuitivo. Los experimentos realizados con estudiantes en clases de gestión de recursos naturales sugieren que las personas que utilizan su experiencia pasada, su intuición y su mejor criterio para gestionar una pesquería generan un rendimiento a largo plazo mucho menor en comparación con una computadora que utiliza un cálculo del RMS, incluso cuando ese cálculo proviene de modelos dinámicos de población incorrectos. [27]
Para una descripción más contemporánea del RMS y su cálculo, consulte [28].
Un ejemplo de errores en la estimación de la dinámica poblacional de una especie ocurrió en la pesquería de reloj anaranjado de Nueva Zelanda . Las primeras cuotas se basaron en la suposición de que el reloj anaranjado tenía una vida bastante corta y se reproducía relativamente rápido. Sin embargo, más tarde se descubrió que el reloj anaranjado vivía mucho tiempo y se reproducía lentamente (unos 30 años). En esa etapa, las poblaciones se habían agotado en gran medida. [ cita requerida ]
Este enfoque ha sido ampliamente criticado por ignorar varios factores clave que intervienen en la gestión de la pesca y ha provocado el colapso devastador de muchas pesquerías. Entre los biólogos conservacionistas se considera que es peligroso y se utiliza incorrectamente. [29] [12]
En todo el mundo hay una crisis en las pesquerías mundiales. [30] En los últimos años se ha observado un declive acelerado en la productividad de muchas pesquerías importantes. [31] Las pesquerías que han sido devastadas en los últimos tiempos incluyen (pero no se limitan a) las grandes pesquerías de ballenas, las pesquerías del Gran Banco del Atlántico occidental y la pesquería de anchoveta peruana. [32] Evaluaciones recientes de la Organización de las Naciones Unidas para la Alimentación y la Agricultura (FAO) del estado de las pesquerías mundiales indican una estabilización de los desembarques en la década de 1990, en alrededor de 100 millones de toneladas. [33]
Además, la composición de las capturas globales ha cambiado. [34] A medida que los pescadores agotan las especies de peces depredadores más grandes y de vida más larga, como el bacalao, el atún, el tiburón y el pargo, pasan al siguiente nivel: a especies que tienden a ser más pequeñas, de vida más corta y menos valiosas. [35]
La sobrepesca es un ejemplo clásico de la tragedia de los bienes comunes . [32]
En ecología y economía de poblaciones , el rendimiento óptimo sostenible es el nivel de esfuerzo (LOE) que maximiza la diferencia entre los ingresos totales y los costos totales, o donde los ingresos marginales son iguales a los costos marginales. Este nivel de esfuerzo maximiza la ganancia económica, o renta, del recurso que se utiliza. Por lo general, corresponde a un nivel de esfuerzo menor que el del rendimiento máximo sostenible. En ciencias ambientales , el rendimiento óptimo sostenible es el mayor rendimiento económico de un recurso renovable alcanzable durante un largo período de tiempo sin disminuir la capacidad de la población o su entorno para sustentar la continuidad de este nivel de rendimiento.