Ecuaciones de Lotka-Volterra

Ecuaciones que modelan los ciclos depredador-presa

Las ecuaciones de Lotka-Volterra , también conocidas como modelo depredador-presa de Lotka-Volterra , son un par de ecuaciones diferenciales no lineales de primer orden , frecuentemente utilizadas para describir la dinámica de sistemas biológicos en los que interactúan dos especies, una como depredador y la otra como depredador . otro como presa. Las poblaciones cambian a través del tiempo según el par de ecuaciones:

$${\displaystyle {\begin{aligned}{\frac {dx}{dt}}&=\alpha x-\beta xy,\\{\frac {dy}{dt}}&=\delta xy-\gamma y,\end{aligned}}}$$

dónde

• la variable x es la densidad de población de presas (por ejemplo, el número de conejos por kilómetro cuadrado);
• la variable y es la densidad de población de algún depredador (por ejemplo, el número de zorros por kilómetro cuadrado);
• ${\displaystyle {\tfrac {dy}{dt}}}$y representan las tasas de crecimiento instantáneo de las dos poblaciones; ${\displaystyle {\tfrac {dx}{dt}}}$
• t representa el tiempo;
• Los parámetros de la presa , α y β , describen, respectivamente, la tasa máxima de crecimiento per cápita de la presa y el efecto de la presencia de depredadores en la tasa de crecimiento de la presa.
• Los parámetros del depredador, γ , δ , describen respectivamente la tasa de mortalidad per cápita del depredador y el efecto de la presencia de presas en la tasa de crecimiento del depredador.
• Todos los parámetros son positivos y reales.

La solución de las ecuaciones diferenciales es determinista y continua . Esto, a su vez, implica que las generaciones tanto del depredador como de la presa se superponen continuamente. ^[1]

El sistema de ecuaciones de Lotka-Volterra es un ejemplo de un modelo de Kolmogorov , ^{[2] [3] [4]} que es un marco más general que puede modelar la dinámica de los sistemas ecológicos con interacciones depredador-presa, competencia , enfermedades y mutualismo. .

Interpretación biológica y supuestos del modelo.

Se supone que las presas tienen un suministro ilimitado de alimentos y se reproducen exponencialmente, a menos que estén sujetas a depredación; este crecimiento exponencial está representado en la ecuación anterior por el término αx . Se supone que la tasa de depredación de la presa es proporcional a la tasa a la que se encuentran los depredadores y la presa; esto está representado arriba por βxy . Si x o y son cero, entonces no puede haber depredación. Con estos dos términos, la ecuación de presa anterior se puede interpretar de la siguiente manera: la tasa de cambio de la población de la presa está dada por su propia tasa de crecimiento menos la tasa a la que es depredada.

El término δxy representa el crecimiento de la población de depredadores. (Obsérvese la similitud con la tasa de depredación; sin embargo, se utiliza una constante diferente, ya que la tasa a la que crece la población de depredadores no es necesariamente igual a la tasa a la que consume la presa). El término γy representa la tasa de pérdida de los depredadores debido a muerte natural o emigración; conduce a una decadencia exponencial en ausencia de presas. Por tanto, la ecuación expresa que la tasa de cambio de la población del depredador depende de la tasa a la que consume a sus presas, menos su tasa de mortalidad intrínseca.

El modelo depredador-presa de Lotka-Volterra hace una serie de suposiciones sobre el medio ambiente y la biología de las poblaciones de depredadores y presas: ^[5]

1. La población de presas encuentra abundante alimento en todo momento.
2. El suministro de alimento de la población de depredadores depende enteramente del tamaño de la población de presas.
3. La tasa de cambio de la población es proporcional a su tamaño.
4. Durante el proceso, el entorno no cambia a favor de una especie y la adaptación genética es intrascendente.
5. Los depredadores tienen un apetito ilimitado.
6. Ambas poblaciones pueden describirse mediante una sola variable. Esto equivale a suponer que las poblaciones no tienen una distribución espacial o etaria que contribuya a la dinámica.

Relevancia biológica del modelo.

Números de pieles de liebre con raquetas de nieve (amarillo, fondo) y lince canadiense (línea negra, primer plano) vendidas a la Hudson's Bay Company . Los linces canadienses comen liebres con raquetas de nieve.

Es probable que ninguno de los supuestos anteriores se cumpla para las poblaciones naturales. Sin embargo, el modelo Lotka-Volterra muestra dos propiedades importantes de las poblaciones de depredadores y presas y estas propiedades a menudo se extienden a variantes del modelo en las que estos supuestos son relajados:

En primer lugar, la dinámica de las poblaciones de depredadores y presas tiende a oscilar. Se han observado números fluctuantes de depredadores y presas en poblaciones naturales, como los datos de linces y liebres con raquetas de nieve de la Compañía de la Bahía de Hudson ^[6] y las poblaciones de alces y lobos en el Parque Nacional Isle Royale . ^[7]

En segundo lugar, el equilibrio poblacional de este modelo tiene la propiedad de que la densidad de equilibrio de la presa (dada por ) depende de los parámetros del depredador, y la densidad de equilibrio del depredador (dada por ) de los parámetros de la presa. Esto tiene como consecuencia que un aumento en, por ejemplo, la tasa de crecimiento de las presas, conduce a un aumento en la densidad de equilibrio de los depredadores, pero no en la densidad de equilibrio de las presas. Mejorar el ambiente para la presa beneficia al depredador, no a la presa (esto está relacionado con la paradoja de los pesticidas y con la paradoja del enriquecimiento ). Una demostración de este fenómeno la proporciona el mayor porcentaje de peces depredadores capturados durante los años de la Primera Guerra Mundial (1914-18), cuando la tasa de crecimiento de las presas aumentó debido a un menor esfuerzo pesquero. ${\displaystyle x=\gamma /\delta }$ ${\displaystyle y=\alpha /\beta }$ ${\displaystyle \alpha }$

Otro ejemplo lo constituye la fertilización experimental del océano con hierro. En varios experimentos se disolvieron grandes cantidades de sales de hierro en el océano. La expectativa era que el hierro, que es un nutriente limitante para el fitoplancton, impulsaría el crecimiento del fitoplancton y secuestraría dióxido de carbono de la atmósfera. La adición de hierro suele provocar una breve floración del fioplancton, que es rápidamente consumido por otros organismos (como peces pequeños o zooplancton ) y limita el efecto del enriquecimiento principalmente a una mayor densidad de depredadores, lo que a su vez limita el secuestro de carbono. Esto es lo que predicen las densidades de población en equilibrio del modelo depredador-presa de Lotka-Volterra, y es una característica que se traslada a modelos más elaborados en los que se relajan los supuestos restrictivos del modelo simple. ^[8]

Aplicaciones a la economía y el marketing

El modelo Lotka Volterra tiene aplicaciones adicionales en áreas como la economía ^[9] y el marketing. ^{[10] [11]} Puede usarse para describir la dinámica en un mercado con varios competidores, plataformas y productos complementarios, una economía colaborativa y más. Hay situaciones en las que uno de los competidores expulsa a los demás competidores del mercado y otras situaciones en las que el mercado alcanza un equilibrio en el que cada empresa estabiliza su participación de mercado. También es posible describir situaciones en las que existen cambios cíclicos en la industria o situaciones caóticas sin equilibrio y los cambios son frecuentes e impredecibles.

Historia

El modelo depredador-presa de Lotka-Volterra fue propuesto inicialmente por Alfred J. Lotka en la teoría de reacciones químicas autocatalíticas en 1910. ^{[12] [13]} Esta era efectivamente la ecuación logística , ^[14] derivada originalmente por Pierre François Verhulst . ^[15] En 1920 Lotka amplió el modelo, a través de Andrey Kolmogorov , a "sistemas orgánicos" utilizando una especie vegetal y una especie animal herbívora como ejemplo ^[16] y en 1925 utilizó las ecuaciones para analizar las interacciones depredador-presa en su libro. sobre biomatemáticas . ^[17] El mismo conjunto de ecuaciones fue publicado en 1926 por Vito Volterra , un matemático y físico, que se había interesado en la biología matemática . ^{[13] [18] [19]} La investigación de Volterra se inspiró en sus interacciones con el biólogo marino Umberto D'Ancona , quien estaba cortejando a su hija en ese momento y más tarde se convertiría en su yerno. D'Ancona estudió las capturas de peces en el mar Adriático y notó que el porcentaje de peces depredadores capturados había aumentado durante los años de la Primera Guerra Mundial (1914-18). Esto lo desconcertó, ya que el esfuerzo de pesca se había reducido mucho durante los años de la guerra y, como los peces de presa eran la captura preferida, uno intuitivamente esperaría que esto aumentara el porcentaje de peces de presa. Volterra desarrolló su modelo para explicar la observación de D'Ancona y lo hizo independientemente de Alfred Lotka. Le dio crédito al trabajo anterior de Lotka en su publicación, después de lo cual el modelo pasó a ser conocido como el "modelo Lotka-Volterra". ^[20]

Posteriormente, el modelo se amplió para incluir el crecimiento de presas dependiente de la densidad y una respuesta funcional de la forma desarrollada por CS Holling ; un modelo que se conoce como modelo Rosenzweig-MacArthur. ^[21] Tanto el modelo de Lotka-Volterra como el de Rosenzweig-MacArthur se han utilizado para explicar la dinámica de las poblaciones naturales de depredadores y presas.

A finales de la década de 1980, surgió una alternativa al modelo depredador-presa de Lotka-Volterra (y sus generalizaciones dependientes de presas comunes), el modelo dependiente de la proporción o modelo Arditi-Ginzburg . ^[22] La validez de los modelos dependientes de la presa o de la proporción ha sido muy debatida. ^[23]

Las ecuaciones de Lotka-Volterra tienen una larga historia de uso en la teoría económica ; su solicitud inicial se atribuye comúnmente a Richard Goodwin en 1965 ^[24] o 1967. ^{[25] [26]}

Soluciones a las ecuaciones.

Las ecuaciones tienen soluciones periódicas . Estas soluciones no tienen una expresión sencilla en términos de las funciones trigonométricas habituales , aunque son bastante manejables. ^{[27] [28] [29]}

Si ninguno de los parámetros no negativos α , β , γ , δ desaparece, se pueden absorber tres en la normalización de variables para dejar solo un parámetro: dado que la primera ecuación es homogénea en x y la segunda en y , los parámetros β / α y δ / γ son absorbibles en las normalizaciones de y y x respectivamente, y γ en la normalización de t , de modo que sólo α / γ permanece arbitrario. Es el único parámetro que afecta la naturaleza de las soluciones.

Una linealización de las ecuaciones produce una solución similar al movimiento armónico simple ^[30] con la población de depredadores siguiendo a la de presas 90° en el ciclo.

Un ejemplo sencillo

Se menciona aparte la dinámica poblacional del problema de los conejos y los zorros.

Gráfico espacio-fase para el problema presa-depredador para diversas condiciones iniciales de la población de depredadores.

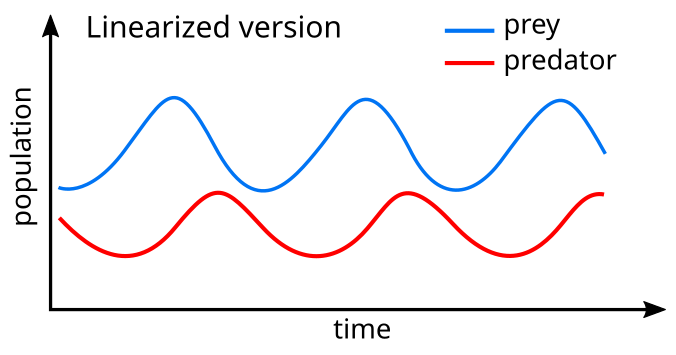
Supongamos que hay dos especies de animales, un conejo (presa) y un zorro (depredador). Si las densidades iniciales son 10 conejos y 10 zorros por kilómetro cuadrado, se puede trazar la progresión de las dos especies a lo largo del tiempo; dados los parámetros que las tasas de crecimiento y muerte de los conejos son 1,1 y 0,4 mientras que las de los zorros son 0,1 y 0,4 respectivamente. La elección del intervalo de tiempo es arbitraria.

También se pueden trazar soluciones paramétricamente como órbitas en el espacio de fases , sin representar el tiempo, pero con un eje representando el número de presas y el otro eje representando las densidades de depredadores para todos los tiempos.

Esto corresponde a eliminar el tiempo de las dos ecuaciones diferenciales anteriores para producir una única ecuación diferencial.

${\displaystyle {\frac {dy}{dx}}=-{\frac {y}{x}}{\frac {\delta x-\gamma }{\beta y-\alpha }}}$

relacionando las variables x e y . Las soluciones de esta ecuación son curvas cerradas. Es susceptible de separación de variables : integración

${\displaystyle {\frac {\beta y-\alpha }{y}}\,dy+{\frac {\delta x-\gamma }{x}}\,dx=0}$

produce la relación implícita

${\displaystyle V=\delta x-\gamma \ln(x)+\beta y-\alpha \ln(y),}$

donde V es una cantidad constante que depende de las condiciones iniciales y se conserva en cada curva.

Una acotación: estos gráficos ilustran una limitación potencial grave en la aplicación como modelo biológico: para esta elección específica de parámetros, en cada ciclo, la población de conejos se reduce a números extremadamente bajos, pero se recupera (mientras que la población de zorros sigue siendo considerable al final). densidad de conejos más baja). Sin embargo, en situaciones de la vida real, las fluctuaciones aleatorias de los números discretos de individuos podrían causar que los conejos se extingan y, en consecuencia, también los zorros. Este problema de modelado se ha denominado "problema del atto-zorro", siendo un atto- zorro un 10 ⁻¹⁸ teórico de un zorro. ^{[31] [32]} Una densidad de 10 ⁻¹⁸ zorros por kilómetro cuadrado equivale a un promedio de aproximadamente 5×10 ⁻¹⁰ zorros en la superficie de la tierra, lo que en términos prácticos significa que los zorros están extintos.

Estructura hamiltoniana del sistema.

Dado que la cantidad se conserva en el tiempo, desempeña el papel de una función hamiltoniana del sistema. ^[33] Para ver esto podemos definir el corchete de Poisson de la siguiente manera . Entonces las ecuaciones de Hamilton leen ${\displaystyle V(x,y)}$ ${\displaystyle \{f,g\}=-xy\left({\frac {\partial f}{\partial x}}{\frac {\partial g}{\partial y}}-{\frac {\partial f}{\partial y}}{\frac {\partial g}{\partial x}}\right)}$

$${\displaystyle {\begin{cases}{\dot {x}}=\{x,V\}=\alpha x-\beta xy,\\{\dot {y}}=\{y,V\}=\delta xy-\gamma y.\end{cases}}}$$

^[34]ecuaciones de Hamilton ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle \{x,y\}=-xy\neq 1}$ ${\displaystyle p=\ln(x)}$ ${\displaystyle q=\ln(y)}$ ${\displaystyle H(q,p)=V(x(q,p),y(q,p))=\delta e^{p}-\gamma p+\beta e^{q}-\alpha q}$

$${\displaystyle {\begin{cases}{\dot {q}}={\frac {\partial H}{\partial p}}=\delta e^{p}-\gamma ,\\{\dot {p}}=-{\frac {\partial H}{\partial q}}=\alpha -\beta e^{q}.\end{cases}}}$$

Gráfico de espacio de fases de otro ejemplo.

Un ejemplo menos extremo cubre:

α = 2/3 , β = 4/3 , γ = 1 = δ . Supongamos que x , y cuantifican miles cada uno. Los círculos representan las condiciones iniciales de presa y depredador desde x = y = 0,9 a 1,8, en pasos de 0,1. El punto fijo está en (1, 1/2).

Dinámica del sistema

En el sistema modelo, los depredadores prosperan cuando las presas son abundantes pero, en última instancia, superan su suministro de alimentos y disminuyen. A medida que la población de depredadores sea baja, la población de presas aumentará nuevamente. Estas dinámicas continúan en un ciclo poblacional de crecimiento y disminución.

Equilibrio poblacional

El equilibrio de la población ocurre en el modelo cuando ninguno de los niveles de población cambia, es decir, cuando ambas derivadas son iguales a 0:

$${\displaystyle x(\alpha -\beta y)=0,}$$

$${\displaystyle -y(\gamma -\delta x)=0.}$$

El sistema de ecuaciones anterior produce dos soluciones:

$${\displaystyle \{y=0,\ \ x=0\}}$$

$${\displaystyle \left\{y={\frac {\alpha }{\beta }},\ \ x={\frac {\gamma }{\delta }}\right\}.}$$

Por tanto, hay dos equilibrios.

La primera solución representa efectivamente la extinción de ambas especies. Si ambas poblaciones están en 0, seguirán estando así indefinidamente. La segunda solución representa un punto fijo en el que ambas poblaciones mantienen sus números actuales distintos de cero y, en el modelo simplificado, lo hacen indefinidamente. Los niveles de población en los que se logra este equilibrio dependen de los valores elegidos de los parámetros α , β , γ y δ .

Estabilidad de los puntos fijos.

La estabilidad del punto fijo en el origen se puede determinar realizando una linealización utilizando derivadas parciales .

La matriz jacobiana del modelo depredador-presa es

$${\displaystyle J(x,y)={\begin{bmatrix}\alpha -\beta y&-\beta x\\\delta y&\delta x-\gamma \end{bmatrix}}.}$$

matriz comunitaria

Primer punto fijo (extinción)

Cuando se evalúa en el estado estacionario de (0, 0) , la matriz jacobiana J se convierte en

$${\displaystyle J(0,0)={\begin{bmatrix}\alpha &0\\0&-\gamma \end{bmatrix}}.}$$

Los valores propios de esta matriz son

$${\displaystyle \lambda _{1}=\alpha ,\quad \lambda _{2}=-\gamma .}$$

En el modelo, α y γ son siempre mayores que cero y, como tal, el signo de los valores propios anteriores siempre será diferente. Por tanto, el punto fijo en el origen es un punto de silla .

La inestabilidad de este punto fijo es importante. Si fuera estable, poblaciones distintas de cero podrían verse atraídas hacia él y, como tal, la dinámica del sistema podría conducir a la extinción de ambas especies en muchos casos de niveles poblacionales iniciales. Sin embargo, como el punto fijo en el origen es un punto de silla y, por tanto, inestable, se deduce que la extinción de ambas especies es difícil en el modelo. (De hecho, esto sólo podría ocurrir si la presa fuera completamente erradicada artificialmente, provocando que los depredadores murieran de hambre. Si los depredadores fueran erradicados, la población de presas crecería sin límites en este modelo simple.) Las poblaciones de presas y depredadores pueden acercarse infinitamente a cero y aun así recuperarse.

Segundo punto fijo (oscilaciones)

La evaluación de J en el segundo punto fijo conduce a

$${\displaystyle J\left({\frac {\gamma }{\delta }},{\frac {\alpha }{\beta }}\right)={\begin{bmatrix}0&-{\frac {\beta \gamma }{\delta }}\\{\frac {\alpha \delta }{\beta }}&0\end{bmatrix}}.}$$

Los valores propios de esta matriz son

$${\displaystyle \lambda _{1}=i{\sqrt {\alpha \gamma }},\quad \lambda _{2}=-i{\sqrt {\alpha \gamma }}.}$$

Como los valores propios son puramente imaginarios y conjugados entre sí, este punto fijo debe ser un centro de órbitas cerradas en las proximidades locales o una espiral atractiva o repulsiva. En sistemas conservadores, debe haber órbitas cerradas en las proximidades locales de puntos fijos que existen en los mínimos y máximos de la cantidad conservada. La cantidad conservada se deduce arriba para estar en órbitas. Así, las órbitas alrededor del punto fijo son cerradas y elípticas , por lo que las soluciones son periódicas, oscilando en una pequeña elipse alrededor del punto fijo, con una frecuencia y un período . ${\displaystyle V=\delta x-\gamma \ln(x)+\beta y-\alpha \ln(y)}$ ${\displaystyle \omega ={\sqrt {\lambda _{1}\lambda _{2}}}={\sqrt {\alpha \gamma }}}$ ${\displaystyle T=2{\pi }/({\sqrt {\lambda _{1}\lambda _{2}}})}$

Como se ilustra en las oscilaciones circulantes en la figura anterior, las curvas de nivel son órbitas cerradas que rodean el punto fijo: los niveles de las poblaciones de depredadores y presas ciclan y oscilan sin amortiguación alrededor del punto fijo con frecuencia . ${\displaystyle \omega ={\sqrt {\alpha \gamma }}}$

El valor de la constante de movimiento V , o, equivalentemente, K = exp(− V ) , se puede encontrar para las órbitas cerradas cerca del punto fijo. ${\displaystyle K=y^{\alpha }e^{-\beta y}x^{\gamma }e^{-\delta x}}$

Al aumentar K, se acerca una órbita cerrada al punto fijo. El mayor valor de la constante K se obtiene resolviendo el problema de optimización.

$${\displaystyle y^{\alpha }e^{-\beta y}x^{\gamma }e^{-\delta x}={\frac {y^{\alpha }x^{\gamma }}{e^{\delta x+\beta y}}}\longrightarrow \max _{x,y>0}.}$$

K ${\displaystyle \left({\frac {\gamma }{\delta }},{\frac {\alpha }{\beta }}\right)}$

$${\displaystyle K^{*}=\left({\frac {\alpha }{\beta e}}\right)^{\alpha }\left({\frac {\gamma }{\delta e}}\right)^{\gamma },}$$

eel número de Euler

Ver también

• Ecuaciones competitivas de Lotka-Volterra
• Ecuación generalizada de Lotka-Volterra
• El mutualismo y la ecuación Lotka-Volterra
• Matriz comunitaria
• Dinámica poblacional
• Dinámica poblacional de las pesquerías.
• Modelo de Nicholson-Bailey
• Sistema de reacción-difusión
• Paradoja del enriquecimiento
• Leyes de Lanchester , un sistema similar de ecuaciones diferenciales para fuerzas militares.

Notas

1. Cooke, D.; Hiorns, RW; et al. (1981). La teoría matemática de la dinámica de las poblaciones biológicas . vol. II. Prensa académica.
2. Freedman, Hola (1980). Modelos matemáticos deterministas en ecología de poblaciones . Marcel Dekker .
3. Brauer, F.; Castillo-Chávez, C. (2000). Modelos matemáticos en biología y epidemiología de poblaciones . Springer-Verlag .
4. Hoppensteadt, F. (2006). "Modelo depredador-presa". Scholarpedia . 1 (10): 1563. Código bibliográfico : 2006SchpJ...1.1563H. doi : 10.4249/scholarpedia.1563 .
5. "DINÁMICA DEPREDADOR-PRESA". www.tiem.utk.edu . Consultado el 9 de enero de 2018 .
6. Gilpin, YO (1973). "¿Las liebres comen linces?". Naturalista americano . 107 (957): 727–730. doi :10.1086/282870. S2CID  84794121.
7. Jost, C.; Devulder, G.; Vucetich, JA; Peterson, R.; Arditi, R. (2005). "Los lobos de Isle Royale muestran saciedad invariable en la escala y depredación de los alces dependiente de la densidad". J.Anim. Ecológico . 74 (5): 809–816. doi :10.1111/j.1365-2656.2005.00977.x.
8. Pan, A.; Pourziaei, B.; Huang, H. (3 de junio de 2015). "Efecto de la fertilización con hierro oceánico sobre la bomba biológica de carbono del fitoplancton". Avances en Matemática y Mecánica Aplicadas . 3 (1): 52–64. doi :10.4208/aamm.10-m1023. S2CID  124606355.
9. Prasolov, Alejandro V. (2016). Algunos métodos y modelos cuantitativos en teoría económica . Cuestiones, problemas y perspectivas económicas. Nueva York: Nova Publishers. ISBN 978-1-63484-937-1.
10. Colgado, Hui-Chih; Chiu, Yu-Chih; Wu, Muh-Cherng (2017). "Un modelo Lotka-Volterra modificado para la difusión y sustitución de tecnologías de procesamiento DRAM multigeneración". Problemas Matemáticos en Ingeniería . 2017 : 1-12. doi : 10.1155/2017/3038203 . ISSN  1024-123X.
11. Orbach, Yair (2022). Previsión de la dinámica del mercado y la tecnología . Israel: Prensa de la Universidad Ariel. págs. 123-143. ISBN 978-965-7632-40-6.
12. Lotka, AJ (1910). "Contribución a la Teoría de la Reacción Periódica". J. Física. Química. 14 (3): 271–274. doi :10.1021/j150111a004.
13. Goel, NS; et al. (1971). Sobre Volterra y otros modelos no lineales de poblaciones que interactúan . Prensa académica. ISBN 0-12-287450-1.
14. Berryman, AA (1992). "Los orígenes y la evolución de la teoría depredador-presa" (PDF) . Ecología . 73 (5): 1530-1535. doi :10.2307/1940005. JSTOR  1940005. Archivado desde el original (PDF) el 31 de mayo de 2010.
15. Verhulst, PH (1838). "Aviso sobre la ley que la población poursuit dans son accroissement". Correspondiente. Matemática y Física . 10 : 113–121.
16. Lotka, AJ (1920). "Nota analítica sobre determinadas relaciones rítmicas en sistemas orgánicos". Proc. Nacional. Acad. Ciencia. Estados Unidos 6 (7): 410–415. Código Bib : 1920PNAS....6..410L. doi : 10.1073/pnas.6.7.410 . PMC 1084562 . PMID  16576509.  
17. Lotka, AJ (1925). Elementos de Biología Física . Williams y Wilkins .
18. Volterra, V. (1926). "Variazioni e fluttuazioni del numero d'individui in specie animali conviventi". Memoria. Acad. Lincei Roma . 2 : 31–113.
19. Volterra, V. (1931). "Variaciones y fluctuaciones del número de individuos de especies animales que conviven". En Chapman, RN (ed.). Ecología animal . McGraw-Hill .
20. Kingsland, S. (1995). Modelado de la naturaleza: episodios de la historia de la ecología de poblaciones . Prensa de la Universidad de Chicago. ISBN 978-0-226-43728-6.
21. Rosenzweig, ML; MacArthur, RH (1963). "Representación gráfica y condiciones de estabilidad de las interacciones depredador-presa". Naturalista americano . 97 (895): 209–223. doi :10.1086/282272. S2CID  84883526.
22. Arditi, R.; Ginzburg, LR (1989). "Acoplamiento en la dinámica depredador-presa: dependencia de la proporción" (PDF) . Revista de Biología Teórica . 139 (3): 311–326. Código Bib : 1989JThBi.139..311A. doi :10.1016/s0022-5193(89)80211-5.
23. Abrams, Pensilvania; Ginzburg, LR (2000). "La naturaleza de la depredación: ¿dependiente de la presa, dependiente de la proporción o ninguna de las dos?". Tendencias en ecología y evolución . 15 (8): 337–341. doi :10.1016/s0169-5347(00)01908-x. PMID  10884706.
24. Gandolfo, G. (2008). "Giuseppe Palomba y las ecuaciones de Lotka-Volterra". Rendiconti Lincei . 19 (4): 347–357. doi :10.1007/s12210-008-0023-7. S2CID  140537163.
25. Goodwin, RM (1967). "Un ciclo de crecimiento" . En Feinstein, CH (ed.). Socialismo, capitalismo y crecimiento económico . Prensa de la Universidad de Cambridge .
26. Desai, M.; Ormerod, P. (1998). "Richard Goodwin: un breve agradecimiento" (PDF) . La Revista Económica . 108 (450): 1431-1435. CiteSeerX 10.1.1.423.1705 . doi :10.1111/1468-0297.00350. Archivado desde el original (PDF) el 27 de septiembre de 2011 . Consultado el 22 de marzo de 2010 . 
27. Steiner, Antonio; Gander, Martín Jakob (1999). "Parametrische Lösungen der Räuber-Beute-Gleichungen im Vergleich". El Volterriano . 7 : 32–44.
28. Evans, CM; Findley, GL (1999). "Una nueva transformación del problema Lotka-Volterra". Revista de Química Matemática . 25 : 105-110. doi :10.1023/A:1019172114300. S2CID  36980176.
29. Leconte, M.; Masón, P.; Qi, L. (2022). "Oscilaciones del ciclo límite, tiempo de respuesta y la solución dependiente del tiempo para el modelo depredador-presa de Lotka-Volterra". Física de Plasmas . 29 (2): 022302. arXiv : 2110.11557 . doi :10.1063/5.0076085. S2CID  239616189.
30. Pinzas, H. (1983). Modelos de umbral en análisis de series temporales no lineales . Springer-Verlag.
31. Lobry, Claude; Sari, Tewfik (2015). "Migraciones en el modelo Rosenzweig-MacArthur y el problema" atto-fox "" (PDF) . Arima . 20 : 95–125.
32. Mollison, D. (1991). "Dependencia de las velocidades epidémicas y poblacionales de parámetros básicos" (PDF) . Matemáticas. Biosci . 107 (2): 255–287. doi :10.1016/0025-5564(91)90009-8. PMID  1806118.
33. Nutku, I. (1990). "Estructura hamiltoniana de las ecuaciones de Lotka-Volterra". Letras de Física A. 145 (1): 27–28. Código bibliográfico : 1990PhLA..145...27N. doi :10.1016/0375-9601(90)90270-X. hdl : 11693/26204 . S2CID  121710034.
34. Baigent, Steve (2 de marzo de 2010). "Dinámica Lotka-Volterra: una introducción" (PDF) .

Otras lecturas

• Hofbauer, Josef; Sigmund, Karl (1998). "Sistemas dinámicos y ecuaciones de Lotka-Volterra". Juegos evolutivos y dinámica de poblaciones . Nueva York: Cambridge University Press. págs. 1–54. ISBN 0-521-62570-X.
• Kaplan, Daniel; Vidrio, León (1995). Comprensión de la dinámica no lineal . Nueva York: Springer. ISBN 978-0-387-94440-1.
• Leigh, ER (1968). "El papel ecológico de las ecuaciones de Volterra". Algunos problemas matemáticos en biología .– una discusión moderna utilizando datos de la Compañía de la Bahía de Hudson sobre linces y liebres en Canadá desde 1847 hasta 1903.
• Murray, JD (2003). Biología Matemática I: Introducción . Nueva York: Springer. ISBN 978-0-387-95223-9.

enlaces externos

• Del Proyecto de demostraciones de Wolfram : requiere un reproductor CDF (gratis):
  • Ecuaciones depredador-presa
  • Modelo depredador-presa
  • Dinámica depredador-presa con respuesta funcional de tipo dos
  • Ecosistema Predator-Prey: una simulación basada en agentes en tiempo real
• Simulación algorítmica Lotka-Volterra (simulación web).