
En geometría , una recta cuadrisecante o cuadrisecante de una curva espacial es una recta que pasa por cuatro puntos de la curva. Este es el mayor número posible de intersecciones que una curva espacial genérica puede tener con una línea, y para tales curvas las cuadrisecantes forman un conjunto discreto de líneas. Se han estudiado cuadrisecantes para curvas de varios tipos:
Una cuadrisecante es una línea que intersecta una curva, superficie u otro conjunto en cuatro puntos distintos. Es análoga a una recta secante , una recta que corta una curva o superficie en dos puntos; y una trisecante , una recta que corta una curva o superficie en tres puntos. [2]
En comparación con las secantes y trisecantes, las cuadrisecantes son especialmente relevantes para las curvas espaciales , porque tienen el mayor número posible de puntos de intersección de una línea con una curva genérica . En el plano, una curva genérica puede ser atravesada arbitrariamente muchas veces por una línea; por ejemplo, pequeñas perturbaciones genéricas de la curva seno son atravesadas infinitamente por el eje horizontal. Por el contrario, si una curva espacial arbitraria se perturba una pequeña distancia para hacerla genérica, no habrá líneas que pasen por cinco o más puntos de la curva perturbada. Sin embargo, cualquier cuadrisecante de la curva espacial original permanecerá presente cerca de su perturbación. [3] Para curvas espaciales genéricas, las cuadrisecantes forman un conjunto discreto de líneas. Por el contrario, cuando ocurren trisecantes, forman familias continuas de líneas. [4]
Una explicación para este fenómeno es visual: mirando una curva espacial desde lejos, el espacio desde tales puntos de vista puede describirse como una esfera bidimensional, con un punto correspondiente a cada dirección. Puede parecer que pares de hilos de la curva se cruzan desde todos estos puntos de vista, o desde un subconjunto bidimensional de ellos. Tres hilos formarán un cruce triple cuando el punto de vista se encuentre en una trisecante, y cuatro hilos formarán un cruce cuádruple desde un punto de vista sobre una cuadrisecante. Cada restricción de que el cruce de un par de hebras se encuentre en otra hebra reduce el número de grados de libertad en uno (para una curva genérica), por lo que los puntos de vista sobre las trisecantes forman un subconjunto unidimensional (continuamente infinito) de la esfera. , mientras que los puntos de vista de las cuadrisecantes forman un subconjunto de dimensión cero (discreto). CTC Wall escribe que el hecho de que las curvas espaciales genéricas sean atravesadas como máximo cuatro veces por líneas es "uno de los teoremas más simples de este tipo", un caso modelo para teoremas análogos en transversales de dimensiones superiores. [3]
Dependiendo de las propiedades de la curva, puede que no tenga cuadrisecantes, que tenga un número finito o un número infinito. Estas consideraciones hacen que sea interesante determinar las condiciones para la existencia de cuadrisecantes, o encontrar límites a su número en diversos casos especiales, como curvas anudadas, [5] [6] curvas algebraicas, [7] o disposiciones de líneas . [8]
En el espacio euclidiano tridimensional , cada nudo o eslabón manso no trivial tiene una cuadrisecante. Originalmente establecido en el caso de polígonos anudados y nudos lisos por Erika Pannwitz , [5] este resultado se extendió a nudos en una posición general adecuada y enlaces con un número de enlace distinto de cero , [6] y más tarde a todos los nudos y enlaces mansos no triviales. [9]
Pannwitz demostró con más fuerza que, para un disco localmente plano que tiene el nudo como límite, el número de singularidades del disco se puede utilizar para construir un límite inferior en el número de cuadrisecantes distintos. La existencia de al menos una cuadrisecante se deriva del hecho de que cualquier disco de este tipo debe tener al menos una singularidad. [5] [10] Morton y Mond (1982) conjeturaron que el número de cuadrisecantes distintas de un nudo dado es siempre al menos , donde es el número de cruce del nudo. [6] [10] Desde entonces se han descubierto contraejemplos de esta conjetura. [10]
Los enlaces de dos componentes tienen cuadrisecantes en las que los puntos de la cuadrisecante aparecen en orden alterno entre los dos componentes, [6] y los nudos no triviales tienen cuadrisecantes en las que los cuatro puntos, ordenados cíclicamente como en el nudo, aparecen en orden a lo largo de la cuadrisecante. [11] La existencia de estas cuadrisecantes alternas se puede utilizar para derivar el teorema de Fáry-Milnor , un límite inferior de la curvatura total de un nudo no trivial. [11] Las cuadrisecantes también se han utilizado para encontrar límites inferiores en la longitud de la cuerda de los nudos. [12]
GT Jin y HS Kim conjeturaron que, cuando una curva anudada tiene un número finito de cuadrisecantes, se puede aproximar con un nudo poligonal equivalente con sus vértices en los puntos donde las cuadrisecantes se cruzan , en el mismo orden en que aparecen . Sin embargo, su conjetura es falsa: de hecho, para cada tipo de nudo, hay una realización en la que esta construcción conduce a un polígono que se intersecta a sí mismo, y otra realización en la que esta construcción produce un nudo de un tipo diferente. [13]
¿ Tiene cada nudo salvaje infinitas cuadrisecantes?
Se ha conjeturado que todo nudo salvaje tiene un número infinito de cuadrisecantes. [9]
Arthur Cayley derivó una fórmula para el número de cuadrisecantes de una curva algebraica en un espacio proyectivo complejo tridimensional , en función de su grado y género . [7] Para una curva de grado y género , el número de cuadrisecantes es [14]
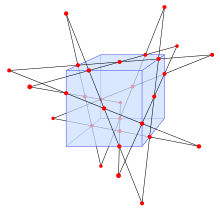
En el espacio euclidiano tridimensional , cada conjunto de cuatro líneas oblicuas en posición general tiene dos cuadrisecantes (también llamadas transversales en este contexto ) o ninguna. Cualesquiera tres de las cuatro líneas determinan un hiperboloide , una superficie doblemente reglada en la que uno de los dos conjuntos de líneas regladas contiene las tres líneas dadas y la otra regla consiste en trisecantes de las líneas dadas. Si la cuarta de las líneas dadas atraviesa esta superficie, tiene dos puntos de intersección, porque el hiperboloide está definido por una ecuación cuadrática . Las dos trisecantes de la superficie reglada, a través de estos dos puntos, forman dos cuadrisecantes de las cuatro rectas dadas. Por otro lado, si la cuarta línea es disjunta del hiperboloide, entonces no hay cuadrisecantes. [17] En espacios con coordenadas de números complejos en lugar de coordenadas reales, cuatro líneas oblicuas siempre tienen exactamente dos cuadrisecantes. [8]
Las cuadrisecantes de conjuntos de líneas juegan un papel importante en la construcción del doble seis de Schläfli , una configuración de doce líneas que se cruzan entre sí en 30 cruces. Si se dan cinco líneas (para ) en un espacio tridimensional, de modo que las cinco estén intersecadas por una línea común pero por lo demás estén en posición general, entonces cada una de las cinco líneas cuádruples tiene una segunda cuadrisecante , y las cinco líneas formadas de esta manera todos son intersecados por una línea común . Estas doce líneas y los 30 puntos de intersección forman el doble seis. [18] [19]
Una disposición de líneas complejas con un número determinado de intersecciones por pares y de otra manera sesgada puede interpretarse como una curva algebraica con grado y género determinados a partir de su número de intersecciones, y la fórmula antes mencionada de Cayley se usa para contar sus cuadrisecantes. El mismo resultado que esta fórmula también se puede obtener clasificando los cuádruples de líneas por sus intersecciones, contando el número de cuadrisecantes para cada tipo de cuádruplo y sumando todos los cuádruples de líneas en el conjunto dado. [8]