Función de pérdida

Relación matemática que asigna un evento de probabilidad a un costo

En optimización matemática y teoría de decisiones , una función de pérdida o función de costo (a veces también llamada función de error) ^[1] es una función que asigna un evento o valores de una o más variables a un número real que representa intuitivamente algún "costo" asociado con el evento. Un problema de optimización busca minimizar una función de pérdida. Una función objetivo es una función de pérdida o su opuesta (en dominios específicos, llamada de diversas formas función de recompensa , función de ganancia , función de utilidad , función de aptitud , etc.), en cuyo caso se debe maximizar. La función de pérdida podría incluir términos de varios niveles de la jerarquía.

En estadística, normalmente se utiliza una función de pérdida para la estimación de parámetros , y el evento en cuestión es alguna función de la diferencia entre los valores estimados y verdaderos para una instancia de datos. El concepto, tan antiguo como Laplace , fue reintroducido en estadística por Abraham Wald a mediados del siglo XX. ^[2] En el contexto de la economía , por ejemplo, esto suele ser el costo económico o el arrepentimiento . En la clasificación , es la penalización por una clasificación incorrecta de un ejemplo. En la ciencia actuarial , se utiliza en un contexto de seguros para modelar los beneficios pagados sobre las primas, particularmente desde los trabajos de Harald Cramér en la década de 1920. ^[3] En el control óptimo , la pérdida es la penalización por no lograr un valor deseado. En la gestión del riesgo financiero , la función se asigna a una pérdida monetaria.

Comparación de funciones de pérdida comunes ( MAE , SMAE , pérdida de Huber y pérdida Log-Cosh) utilizadas para la regresión

Ejemplos

Arrepentirse

Leonard J. Savage argumentó que utilizando métodos no bayesianos como el minimax , la función de pérdida debería basarse en la idea del arrepentimiento , es decir, la pérdida asociada a una decisión debería ser la diferencia entre las consecuencias de la mejor decisión que podría haberse tomado si se hubieran conocido las circunstancias subyacentes y la decisión que de hecho se tomó antes de que se conocieran.

Función de pérdida cuadrática

El uso de una función de pérdida cuadrática es común, por ejemplo, cuando se utilizan técnicas de mínimos cuadrados . A menudo es más manejable matemáticamente que otras funciones de pérdida debido a las propiedades de las varianzas , además de ser simétrica: un error por encima del objetivo causa la misma pérdida que la misma magnitud de error por debajo del objetivo. Si el objetivo es t , entonces una función de pérdida cuadrática es

${\displaystyle \lambda (x)=C(t-x)^{2}\;}$

para alguna constante C ; el valor de la constante no hace ninguna diferencia en una decisión y se puede ignorar estableciéndolo igual a 1. Esto también se conoce como pérdida de error al cuadrado ( SEL ). ^[1]

Muchas estadísticas comunes , incluidas las pruebas t , los modelos de regresión , el diseño de experimentos y mucho más, utilizan métodos de mínimos cuadrados aplicados mediante la teoría de regresión lineal , que se basa en la función de pérdida cuadrática.

La función de pérdida cuadrática también se utiliza en problemas de control óptimo lineal-cuadrático . En estos problemas, incluso en ausencia de incertidumbre, puede que no sea posible lograr los valores deseados de todas las variables objetivo. A menudo, la pérdida se expresa como una forma cuadrática en las desviaciones de las variables de interés de sus valores deseados; este enfoque es manejable porque da como resultado condiciones lineales de primer orden . En el contexto del control estocástico , se utiliza el valor esperado de la forma cuadrática. La pérdida cuadrática asigna más importancia a los valores atípicos que a los datos verdaderos debido a su naturaleza cuadrada, por lo que se utilizan alternativas como las pérdidas de Huber , Log-Cosh y SMAE cuando los datos tienen muchos valores atípicos grandes.

Efecto de utilizar diferentes funciones de pérdida, cuando los datos tienen valores atípicos.

Función de pérdida 0-1

En estadística y teoría de decisiones , una función de pérdida utilizada con frecuencia es la función de pérdida 0-1.

${\displaystyle L({\hat {y}},y)=\left[{\hat {y}}\neq y\right]}$

utilizando la notación de corchetes de Iverson , es decir, se evalúa como 1 cuando , y 0 en caso contrario. ${\displaystyle {\hat {y}}\neq y}$

Construcción de funciones de pérdida y objetivo

En muchas aplicaciones, las funciones objetivo, incluidas las funciones de pérdida como un caso particular, están determinadas por la formulación del problema. En otras situaciones, la preferencia del decisor debe obtenerse y representarse mediante una función escalar (también llamada función de utilidad ) en una forma adecuada para la optimización, el problema que Ragnar Frisch destacó en su discurso del Premio Nobel. ^[4] Los métodos existentes para construir funciones objetivo se recogen en las actas de dos conferencias dedicadas a ello. ^{[5] [6]} En particular, Andranik Tangian demostró que las funciones objetivo más utilizables (cuadráticas y aditivas) están determinadas por unos pocos puntos de indiferencia. Utilizó esta propiedad en los modelos para construir estas funciones objetivo a partir de datos ordinales o cardinales que se obtuvieron a través de entrevistas asistidas por ordenador con decisores. ^{[7] [8]} Entre otras cosas, construyó funciones objetivo para distribuir de forma óptima los presupuestos de 16 universidades de Westfalia ^[9] y los subsidios europeos para igualar las tasas de desempleo entre 271 regiones alemanas. ^[10]

Pérdida esperada

En algunos contextos, el valor de la función de pérdida en sí es una cantidad aleatoria porque depende del resultado de una variable aleatoria X.

Estadística

Tanto la teoría estadística frecuentista como la bayesiana implican tomar una decisión basada en el valor esperado de la función de pérdida; sin embargo, esta cantidad se define de manera diferente en los dos paradigmas.

Pérdida esperada frecuentista

Primero definimos la pérdida esperada en el contexto frecuentista. Se obtiene tomando el valor esperado con respecto a la distribución de probabilidad , P _θ , de los datos observados, X . Esto también se conoce como la función de riesgo ^{[11] [12] [13] [14]} de la regla de decisión δ y el parámetro θ . Aquí la regla de decisión depende del resultado de X . La función de riesgo está dada por:

${\displaystyle R(\theta ,\delta )=\operatorname {E} _{\theta }L{\big (}\theta ,\delta (X){\big )}=\int _{X}L{\big (}\theta ,\delta (x){\big )}\,\mathrm {d} P_{\theta }(x).}$

Aquí, θ es un estado de la naturaleza fijo pero posiblemente desconocido, X es un vector de observaciones extraídas estocásticamente de una población , es la expectativa sobre todos los valores de población de X , dP _θ es una medida de probabilidad sobre el espacio de eventos de X ( parametrizado por  θ ) y la integral se evalúa sobre todo el soporte de  X. ${\displaystyle \operatorname {E} _{\theta }}$

Riesgo de Bayes

En un enfoque bayesiano, la expectativa se calcula utilizando la distribución previa π ^* del parámetro  θ :

${\displaystyle \rho (\pi ^{*},a)=\int _{\Theta }\int _{\mathbf {X}}L(\theta ,a({\mathbf {x}}))\,\mathrm {d} P({\mathbf {x}}\vert \theta )\,\mathrm {d} \pi ^{*}(\theta )=\int _{\mathbf {X}}\int _{\Theta }L(\theta ,a({\mathbf {x}}))\,\mathrm {d} \pi ^{*}(\theta \vert {\mathbf {x}})\,\mathrm {d} M({\mathbf {x}})}$

donde m(x) se conoce como la probabilidad predictiva en la que θ se ha "integrado", π ^* (θ | x) es la distribución posterior y se ha cambiado el orden de integración. Entonces se debe elegir la acción a ^* que minimiza esta pérdida esperada, a la que se hace referencia como Riesgo de Bayes ^[12] . En la última ecuación, el integrando dentro de dx se conoce como Riesgo posterior y minimizarlo con respecto a la decisión a también minimiza el Riesgo de Bayes general. Esta decisión óptima, a ^* se conoce como la Regla (decisión) de Bayes : minimiza la pérdida promedio sobre todos los estados de naturaleza posibles θ, sobre todos los resultados de datos posibles (ponderados por probabilidad). Una ventaja del enfoque bayesiano es que solo se necesita elegir la acción óptima bajo los datos observados reales para obtener una uniformemente óptima, mientras que elegir la regla de decisión óptima frecuentista real como una función de todas las observaciones posibles, es un problema mucho más difícil. Sin embargo, de igual importancia es que la regla de Bayes refleja la consideración de los resultados de pérdidas en diferentes estados de la naturaleza, θ.

Ejemplos en estadística

• Para un parámetro escalar θ , una función de decisión cuya salida es una estimación de  θ , y una función de pérdida cuadrática ( pérdida de error al cuadrado ) la función de riesgo se convierte en el error cuadrático medio de la estimación. Un estimador que se encuentra al minimizar el error cuadrático medio estima la media de la distribución posterior . ${\displaystyle {\hat {\theta }}}$ $${\displaystyle L(\theta ,{\hat {\theta }})=(\theta -{\hat {\theta }})^{2},}$$ $${\displaystyle R(\theta ,{\hat {\theta }})=\operatorname {E} _{\theta }(\theta -{\hat {\theta }})^{2}.}$$
• En la estimación de densidad , el parámetro desconocido es la densidad de probabilidad en sí. La función de pérdida se elige normalmente como una norma en un espacio de funciones adecuado . Por ejemplo, para la norma L 2 , la función de riesgo se convierte en el error cuadrático medio integrado $${\displaystyle L(f,{\hat {f}})=\|f-{\hat {f}}\|_{2}^{2}\,,}$$ $${\displaystyle R(f,{\hat {f}})=\operatorname {E} \|f-{\hat {f}}\|^{2}.\,}$$

La elección económica en condiciones de incertidumbre

En economía, la toma de decisiones en condiciones de incertidumbre suele modelarse utilizando la función de utilidad de von Neumann-Morgenstern de la variable incierta de interés, como la riqueza al final del período. Como el valor de esta variable es incierto, también lo es el valor de la función de utilidad; lo que se maximiza es el valor esperado de la utilidad.

Reglas de decisión

Una regla de decisión permite tomar una decisión utilizando un criterio de optimalidad. Algunos criterios que se utilizan habitualmente son:

• Minimax : elija la regla de decisión con la menor pérdida peor, es decir, minimice la pérdida en el peor de los casos (máxima posible): $${\displaystyle {\underset {\delta }{\operatorname {arg\,min} }}\ \max _{\theta \in \Theta }\ R(\theta ,\delta ).}$$
• Invariancia : elija la regla de decisión que satisfaga un requisito de invariancia.
• Elija la regla de decisión con la pérdida promedio más baja (es decir, minimice el valor esperado de la función de pérdida): $${\displaystyle {\underset {\delta }{\operatorname {arg\,min} }}\operatorname {E} _{\theta \in \Theta }[R(\theta ,\delta )]={\underset {\delta }{\operatorname {arg\,min} }}\ \int _{\theta \in \Theta }R(\theta ,\delta )\,p(\theta )\,d\theta .}$$

Seleccionar una función de pérdida

Una buena práctica estadística exige seleccionar un estimador coherente con la variación aceptable real que se experimenta en el contexto de un problema aplicado en particular. Por lo tanto, en el uso aplicado de funciones de pérdida, la selección del método estadístico que se utilizará para modelar un problema aplicado depende de conocer las pérdidas que se experimentarán por equivocarse en las circunstancias particulares del problema. ^[15]

Un ejemplo común es la estimación de la " ubicación ". Según supuestos estadísticos típicos, la media o el promedio es la estadística para estimar la ubicación que minimiza la pérdida esperada experimentada según la función de pérdida de error cuadrático , mientras que la mediana es el estimador que minimiza la pérdida esperada experimentada según la función de pérdida de diferencia absoluta. Aun así, otros estimadores serían óptimos en otras circunstancias menos comunes.

En economía, cuando un agente es neutral al riesgo , la función objetivo se expresa simplemente como el valor esperado de una cantidad monetaria, como una ganancia, un ingreso o una riqueza al final del período. Para los agentes que son reacios al riesgo o que lo aman , la pérdida se mide como el negativo de una función de utilidad , y la función objetivo que se debe optimizar es el valor esperado de la utilidad.

Son posibles otras medidas de costos, por ejemplo la mortalidad o la morbilidad en el campo de la salud pública o la ingeniería de seguridad .

Para la mayoría de los algoritmos de optimización , es deseable tener una función de pérdida que sea globalmente continua y diferenciable .

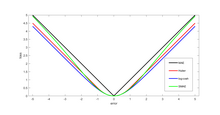
Dos funciones de pérdida muy utilizadas son la pérdida al cuadrado , , y la pérdida absoluta , . Sin embargo, la pérdida absoluta tiene la desventaja de que no es diferenciable en . La pérdida al cuadrado tiene la desventaja de que tiene la tendencia a estar dominada por valores atípicos : cuando se suma sobre un conjunto de (como en ), la suma final tiende a ser el resultado de unos pocos valores a particularmente grandes , en lugar de una expresión del valor a promedio . ${\displaystyle L(a)=a^{2}}$ ${\displaystyle L(a)=|a|}$ ${\displaystyle a=0}$ ${\displaystyle a}$ ${\textstyle \sum _{i=1}^{n}L(a_{i})}$

La elección de una función de pérdida no es arbitraria. Es muy restrictiva y, a veces, la función de pérdida puede caracterizarse por sus propiedades deseables. ^[16] Entre los principios de elección se encuentran, por ejemplo, el requisito de completitud de la clase de estadísticas simétricas en el caso de observaciones iid , el principio de información completa y algunos otros.

W. Edwards Deming y Nassim Nicholas Taleb sostienen que la realidad empírica, no las buenas propiedades matemáticas, debería ser la única base para seleccionar funciones de pérdida, y las pérdidas reales a menudo no son buenas desde el punto de vista matemático y no son diferenciables, continuas, simétricas, etc. Por ejemplo, una persona que llega antes del cierre de la puerta de un avión puede alcanzarlo, pero una persona que llega después no puede, una discontinuidad y asimetría que hace que llegar un poco tarde sea mucho más costoso que llegar un poco antes. En la dosificación de fármacos, el costo de una cantidad insuficiente de fármaco puede ser la falta de eficacia, mientras que el costo de una cantidad excesiva puede ser una toxicidad tolerable, otro ejemplo de asimetría. El tráfico, las tuberías, las vigas, las ecologías, los climas, etc. pueden tolerar una mayor carga o estrés con pocos cambios perceptibles hasta cierto punto, para luego atascarse o romperse catastróficamente. Estas situaciones, sostienen Deming y Taleb, son comunes en los problemas de la vida real, tal vez más comunes que los casos clásicos de diferenciales suaves, continuos y simétricos. ^[17]

Véase también

• Arrepentimiento bayesiano
• Funciones de pérdida para la clasificación
• Pérdida máxima descontada
• Pérdida de bisagra
• Regla de puntuación
• Riesgo estadístico

Referencias

1. Hastie, Trevor; Tibshirani, Robert ; Friedman, Jerome H. (2001). Los elementos del aprendizaje estadístico. Springer. pág. 18. ISBN 0-387-95284-5.
2. Wald, A. (1950). Funciones de decisión estadística. Wiley.
3. Cramér, H. (1930). Sobre la teoría matemática del riesgo . Centraltryckeriet.
4. Frisch, Ragnar (1969). «De la teoría utópica a las aplicaciones prácticas: el caso de la econometría». La conferencia del Premio Nobel . Consultado el 15 de febrero de 2021 .
5. Tangian, Andranik; Gruber, Josef (1997). Construcción de funciones objetivo con valores escalares. Actas de la Tercera Conferencia Internacional sobre Modelos de Decisión Econométrica: Construcción de funciones objetivo con valores escalares, Universidad de Hagen, celebrada en la Katholische Akademie Schwerte del 5 al 8 de septiembre de 1995. Apuntes de la conferencia sobre economía y sistemas matemáticos. Vol. 453. Berlín: Springer. doi :10.1007/978-3-642-48773-6. ISBN . 978-3-540-63061-6.
6. Tangian, Andranik; Gruber, Josef (2002). Construcción y aplicación de funciones objetivas. Actas de la Cuarta Conferencia Internacional sobre Modelos de Decisión Econométrica Construcción y aplicación de funciones objetivas, Universidad de Hagen, celebrada en Haus Nordhelle, del 28 al 31 de agosto de 2000. Apuntes de clase sobre economía y sistemas matemáticos. Vol. 510. Berlín: Springer. doi :10.1007/978-3-642-56038-5. ISBN 978-3-540-42669-1.
7. Tangian, Andranik (2002). "Construcción de una función objetivo cuadrática cuasi-cóncava a partir de una entrevista a un tomador de decisiones". Revista Europea de Investigación Operativa . 141 (3): 608–640. doi :10.1016/S0377-2217(01)00185-0. S2CID  39623350.
8. Tangian, Andranik (2004). "Un modelo para construir ordinalmente funciones objetivo aditivas". Revista Europea de Investigación Operativa . 159 (2): 476–512. doi :10.1016/S0377-2217(03)00413-2. S2CID  31019036.
9. Tangian, Andranik (2004). "Redistribución de los presupuestos universitarios con respecto al status quo". Revista Europea de Investigación Operativa . 157 (2): 409–428. doi :10.1016/S0377-2217(03)00271-6.
10. Tangian, Andranik (2008). "Optimización multicriterio de la política regional de empleo: un análisis de simulación para Alemania". Revista de Desarrollo Urbano y Regional . 20 (2): 103–122. doi :10.1111/j.1467-940X.2008.00144.x.
11. Nikulin, MS (2001) [1994], "Riesgo de un procedimiento estadístico", Enciclopedia de Matemáticas , EMS Press
12. Berger, James O. (1985). Teoría de la decisión estadística y análisis bayesiano (2.ª ed.). Nueva York: Springer-Verlag. Bibcode :1985sdtb.book.....B. ISBN 978-0-387-96098-2.Sr. 0804611  .
13. DeGroot, Morris (2004) [1970]. Decisiones estadísticas óptimas . Biblioteca clásica de Wiley. ISBN 978-0-471-68029-1.Señor 2288194  .
14. Robert, Christian P. (2007). La elección bayesiana . Springer Texts in Statistics (2.ª ed.). Nueva York: Springer. doi :10.1007/0-387-71599-1. ISBN. 978-0-387-95231-4.Señor 1835885  .
15. Pfanzagl, J. (1994). Teoría estadística paramétrica . Berlín: Walter de Gruyter. ISBN 978-3-11-013863-4.
16. Se proporciona información detallada sobre los principios matemáticos de la elección de la función de pérdida en el Capítulo 2 del libro Klebanov, B.; Rachev, Svetlozat T.; Fabozzi, Frank J. (2009). Modelos robustos y no robustos en estadística . Nueva York: Nova Scientific Publishers, Inc.(y referencias allí).
17. Deming, W. Edwards (2000). Salir de la crisis . The MIT Press. ISBN 9780262541152.

Lectura adicional

• Aretz, Kevin; Bartram, Söhnke M.; Pope, Peter F. (abril–junio de 2011). "Funciones de pérdida asimétricas y racionalidad de los rendimientos esperados de las acciones" (PDF) . Revista internacional de previsión . 27 (2): 413–437. doi :10.1016/j.ijforecast.2009.10.008. SSRN  889323.
• Berger, James O. (1985). Teoría de la decisión estadística y análisis bayesiano (2.ª ed.). Nueva York: Springer-Verlag. Bibcode :1985sdtb.book.....B. ISBN 978-0-387-96098-2.Sr. 0804611  .

• Cecchetti, S. (2000). "Elaboración de política monetaria: objetivos y reglas". Oxford Review of Economic Policy . 16 (4): 43–59. doi :10.1093/oxrep/16.4.43.

• Horowitz, Ann R. (1987). "Funciones de pérdida y políticas públicas". Journal of Macroeconomics . 9 (4): 489–504. doi :10.1016/0164-0704(87)90016-4.

• Waud, Roger N. (1976). "Funciones de utilidad asimétricas de los responsables de políticas y política óptima en condiciones de incertidumbre". Econometrica . 44 (1): 53–66. doi :10.2307/1911380. JSTOR  1911380.