Red sin escala

Red cuya distribución de grados sigue una ley de potencia

Distribución de grados para una red con 150.000 vértices y grado medio = 6 creada mediante el modelo de Barabási–Albert (puntos azules). La distribución sigue una forma analítica dada por la relación de dos funciones gamma (línea negra) que se aproxima a una ley de potencia.

Una red libre de escala es una red cuya distribución de grados sigue una ley de potencia , al menos asintóticamente. Es decir, la fracción P ( k ) de nodos en la red que tienen k conexiones con otros nodos es igual para valores grandes de k

${\displaystyle P(k)\ \sim \ k^{\boldsymbol {-\gamma }}}$

donde es un parámetro cuyo valor está típicamente en el rango (donde el segundo momento ( parámetro de escala ) de es infinito pero el primer momento es finito), aunque ocasionalmente puede estar fuera de estos límites. ^{[1] [2]} El nombre "libre de escala" podría explicarse por el hecho de que algunos momentos de la distribución de grados no están definidos, de modo que la red no tiene una escala o "tamaño" característico. ${\displaystyle \gamma }$ ${\textstyle 2<\gamma <3}$ ${\displaystyle k^{\boldsymbol {-\gamma }}}$

Se ha informado que muchas redes son libres de escala, aunque el análisis estadístico ha refutado muchas de estas afirmaciones y ha cuestionado seriamente otras. ^{[3] [4]} Además, algunos han argumentado que simplemente saber que una distribución de grados es de cola gruesa es más importante que saber si una red es libre de escala según definiciones estadísticamente rigurosas. ^{[5] [6]} La fijación preferencial y el modelo de aptitud se han propuesto como mecanismos para explicar las distribuciones de grados de ley de potencia conjeturadas en redes reales. Modelos alternativos como la fijación preferencial superlineal y la fijación preferencial de segundo vecino pueden parecer generar redes libres de escala transitorias, pero la distribución de grados se desvía de una ley de potencia a medida que las redes se vuelven muy grandes. ^{[7] [8]}

Historia

En estudios sobre las redes de citas entre artículos científicos, Derek de Solla Price demostró en 1965 que el número de enlaces a artículos (es decir, el número de citas que reciben) tenía una distribución de cola pesada siguiendo una distribución de Pareto o ley de potencia y, por lo tanto, que la red de citas es libre de escala. Sin embargo, no utilizó el término "red libre de escala", que no se acuñó hasta algunas décadas después. En un artículo posterior de 1976, Price también propuso un mecanismo para explicar la aparición de leyes de potencia en las redes de citas, al que llamó "ventaja acumulativa", pero que hoy en día se conoce más comúnmente con el nombre de apego preferencial .

El interés reciente en las redes sin escala comenzó en 1999 con el trabajo de Albert-László Barabási y Réka Albert en la Universidad de Notre Dame, quienes mapearon la topología de una parte de la World Wide Web ^[9] , encontrando que algunos nodos, que ellos llamaron "centros", tenían muchas más conexiones que otros y que la red en su conjunto tenía una distribución de ley de potencia del número de enlaces que conectaban a un nodo. Después de encontrar que algunas otras redes, incluyendo algunas redes sociales y biológicas, también tenían distribuciones de grado de cola pesada, Barabási y Réka Albert acuñaron el término "red sin escala" para describir la clase de redes que exhiben una distribución de grado de ley de potencia. Sin embargo, al estudiar siete ejemplos de redes en sistemas sociales, económicos, tecnológicos, biológicos y físicos, Amaral et al. no pudieron encontrar una red sin escala entre estos siete ejemplos. Sólo uno de estos ejemplos, la red de actores de películas, tenía una distribución de grados P ( k ) que seguía un régimen de ley de potencia para un valor k moderado , aunque eventualmente este régimen de ley de potencia fue seguido por un corte abrupto que mostraba un decaimiento exponencial para un valor k grande . ^[10]

Barabási y Réka Albert propusieron un mecanismo generativo para explicar la aparición de distribuciones de ley de potencia, al que llamaron " adjunto preferencial " y que es esencialmente el mismo que el propuesto por Price. Las soluciones analíticas para este mecanismo (también similares a la solución de Price) fueron presentadas en 2000 por Dorogovtsev, Mendes y Samukhin ^[11] e independientemente por Krapivsky, Redner y Leyvraz, y luego rigurosamente demostradas por el matemático Béla Bollobás ^[12] . Cabe destacar, sin embargo, que este mecanismo solo produce un subconjunto específico de redes en la clase libre de escala, y desde entonces se han descubierto muchos mecanismos alternativos ^{[13] .}

La historia de las redes sin escala también incluye algunos desacuerdos. A nivel empírico, se ha puesto en tela de juicio la naturaleza sin escala de varias redes. Por ejemplo, los tres hermanos Faloutsos creían que Internet tenía una distribución de grados de ley de potencia sobre la base de los datos de traceroute ; sin embargo, se ha sugerido que se trata de una ilusión de capa 3 creada por los enrutadores, que aparecen como nodos de alto grado mientras ocultan la estructura interna de capa 2 de los AS que interconectan. ^[14]

En un nivel teórico, se han propuesto mejoras a la definición abstracta de escala libre. Por ejemplo, Li et al. (2005) ofrecieron una "métrica de escala libre" potencialmente más precisa. Brevemente, sea G un grafo con un conjunto de aristas E , y denotemos el grado de un vértice (es decir, el número de aristas incidentes a ) por . Definir ${\displaystyle v}$ ${\displaystyle v}$ ${\displaystyle \deg(v)}$

${\displaystyle s(G)=\sum _{(u,v)\in E}\deg(u)\cdot \deg(v).}$

Esto se maximiza cuando los nodos de alto grado están conectados a otros nodos de alto grado. Ahora defina

${\displaystyle S(G)={\frac {s(G)}{s_{\max }}},}$

donde s _max es el valor máximo de s ( H ) para H en el conjunto de todos los grafos con distribución de grados idéntica a la de  G . Esto da una métrica entre 0 y 1, donde un grafo G con S ( G ) pequeño es "rico en escala", y un grafo G con S ( G ) cercano a 1 es "libre de escala". Esta definición captura la noción de autosimilitud implícita en el nombre "libre de escala".

Descripción general

Cuando el concepto de "libre de escala" se introdujo inicialmente en el contexto de las redes, ^[9] se refería principalmente a un rasgo específico: una distribución de ley de potencia para una variable dada , expresada como . Esta propiedad mantiene su forma cuando se somete a una transformación de escala continua , lo que evoca paralelismos con las técnicas de grupo de renormalización en la teoría de campos estadísticos. ^{[15] [16]} ${\displaystyle k}$ ${\displaystyle f(k)\propto k^{-\gamma }}$ ${\displaystyle k\to k+\epsilon k}$

Sin embargo, existe una diferencia clave. En la teoría estadística de campos, el término "escala" suele referirse al tamaño del sistema. En el ámbito de las redes, la "escala" es una medida de conectividad, generalmente cuantificada por el grado de un nodo, es decir, la cantidad de enlaces conectados a él. Se considera que las redes que cuentan con una mayor cantidad de nodos de alto grado tienen mayor conectividad. ${\displaystyle k}$

La distribución de grados de ley de potencia nos permite hacer afirmaciones "libres de escala" sobre la prevalencia de nodos de alto grado. ^[17] Por ejemplo, podemos decir que "los nodos con el triple de la conectividad promedio ocurren con la mitad de frecuencia que los nodos con conectividad promedio". El valor numérico específico de lo que constituye la "conectividad promedio" se vuelve irrelevante, ya sea cien o un millón. ^[18]

Características

Red aleatoria (a) y red libre de escala (b)

Distribución de grados de red compleja aleatoria y libre de escala

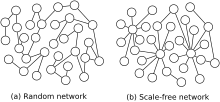
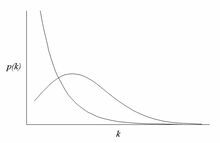
La característica más notable de una red sin escala es la relativa frecuencia de vértices con un grado que supera ampliamente el promedio. Los nodos de grado más alto suelen denominarse "centros" y se cree que cumplen funciones específicas en sus redes, aunque esto depende en gran medida del dominio.

Agrupamiento

Otra característica importante de las redes libres de escala es la distribución del coeficiente de agrupamiento , que disminuye a medida que aumenta el grado del nodo. Esta distribución también sigue una ley de potencia. Esto implica que los nodos de bajo grado pertenecen a subgrafos muy densos y esos subgrafos están conectados entre sí a través de centros. Considere una red social en la que los nodos son personas y los enlaces son relaciones de conocimiento entre personas. Es fácil ver que las personas tienden a formar comunidades, es decir, pequeños grupos en los que todos se conocen (se puede pensar en dicha comunidad como un grafo completo ). Además, los miembros de una comunidad también tienen algunas relaciones de conocimiento con personas fuera de esa comunidad. Algunas personas, sin embargo, están conectadas a un gran número de comunidades (por ejemplo, celebridades, políticos). Esas personas pueden considerarse los centros responsables del fenómeno del mundo pequeño .

En la actualidad, las características más específicas de las redes sin escala varían según el mecanismo generativo utilizado para crearlas. Por ejemplo, las redes generadas por conexión preferencial suelen colocar los vértices de alto grado en el medio de la red, conectándolos entre sí para formar un núcleo, con nodos de grado progresivamente menor que conforman las regiones entre el núcleo y la periferia. La eliminación aleatoria de incluso una gran fracción de vértices afecta muy poco la conectividad general de la red, lo que sugiere que dichas topologías podrían ser útiles para la seguridad , mientras que los ataques dirigidos destruyen la conectividad muy rápidamente. Otras redes sin escala, que colocan los vértices de alto grado en la periferia, no exhiben estas propiedades. De manera similar, el coeficiente de agrupamiento de las redes sin escala puede variar significativamente dependiendo de otros detalles topológicos.

Inmunización

La cuestión de cómo inmunizar de manera eficiente redes libres y escalables que representan redes realistas como Internet y las redes sociales ha sido estudiada extensamente. Una de esas estrategias es inmunizar los nodos de mayor grado, es decir, los ataques dirigidos (intencionados) ya que para este caso p es relativamente alto y se necesitan menos nodos para inmunizar. Sin embargo, en muchos casos realistas la estructura global no está disponible y no se conocen los nodos de mayor grado. ${\displaystyle c}$

Las propiedades de un grafo aleatorio pueden cambiar o permanecer invariables bajo transformaciones de grafos. Mashaghi A. et al., por ejemplo, demostraron que una transformación que convierte grafos aleatorios en sus grafos duales de aristas (o grafos lineales) produce un conjunto de grafos con una distribución de grados casi igual, pero con correlaciones de grados y un coeficiente de agrupamiento significativamente mayor. Los grafos libres de escala, como tales, permanecen libres de escala bajo tales transformaciones. ^[19]

Ejemplos

Aunque se cree que muchas redes del mundo real son libres de escala, la evidencia a menudo no es concluyente, principalmente debido a la creciente conciencia de técnicas de análisis de datos más rigurosas. ^[3] Por ello, la naturaleza libre de escala de muchas redes aún está siendo debatida por la comunidad científica. Algunos ejemplos de redes que se afirma que son libres de escala incluyen:

• Algunas redes sociales , incluidas las redes de colaboración. Dos ejemplos que se han estudiado ampliamente son la colaboración de actores de cine en películas y la coautoría de artículos por parte de matemáticos .
• Muchos tipos de redes de computadoras , incluidas Internet y el webgraph de la World Wide Web .
• Algunas redes financieras como las redes de pagos interbancarios ^{[20] [21]}
• Redes de interacción proteína-proteína .
• Redes semánticas . ^[22]
• Redes de aerolíneas.

Una instantánea de la red estocástica planar ponderada (WPSL)

También se ha encontrado topología libre de escala en superconductores de alta temperatura. ^[23] Las cualidades de un superconductor de alta temperatura —un compuesto en el que los electrones obedecen las leyes de la física cuántica y fluyen en perfecta sincronía, sin fricción— parecen estar vinculadas a las disposiciones fractales de átomos de oxígeno aparentemente aleatorios y a la distorsión reticular. ^[24]

Recientemente se ha propuesto una estructura celular que llena el espacio, la red estocástica plana ponderada (WPSL), cuya distribución de números de coordinación sigue una ley de potencia. Esto implica que la red tiene unos pocos bloques que tienen un número sorprendentemente grande de vecinos con los que comparten bordes comunes. Su construcción comienza con un iniciador, digamos un cuadrado de área unitaria, y un generador que lo divide aleatoriamente en cuatro bloques. A partir de ahí, el generador se aplica secuencialmente una y otra vez a solo uno de los bloques disponibles elegidos preferentemente con respecto a sus áreas. El resultado es la partición del cuadrado en bloques rectangulares mutuamente excluyentes cada vez más pequeños. El dual de la WPSL (DWPSL), que se obtiene reemplazando cada bloque con un nodo en su centro y cada borde común entre bloques con una arista que une los dos vértices correspondientes, surge como una red cuya distribución de grados sigue una ley de potencia. ^{[25] [26]} La razón de ello es que crece siguiendo la regla del modelo de apego impulsado por la mediación que también incorpora la regla del apego preferencial, pero disfrazada.

Modelos generativos

Las redes libres de escala no surgen por pura casualidad. Erdős y Rényi (1960) estudiaron un modelo de crecimiento para grafos en el que, en cada paso, se eligen dos nodos de manera uniforme y aleatoria y se inserta un enlace entre ellos. Las propiedades de estos grafos aleatorios son diferentes de las propiedades que se encuentran en las redes libres de escala, por lo que se necesita un modelo para este proceso de crecimiento.

El modelo generativo más conocido para un subconjunto de redes libres de escala es el modelo generativo de enriquecimiento enriquecido de Barabási y Albert (1999) en el que cada nueva página web crea enlaces a páginas web existentes con una distribución de probabilidad que no es uniforme, sino proporcional al grado de entrada actual de las páginas web. Este modelo fue inventado originalmente por Derek J. de Solla Price en 1965 bajo el término ventaja acumulativa , pero no alcanzó popularidad hasta que Barabási redescubrió los resultados bajo su nombre actual ( modelo BA ). Según este proceso, una página con muchos enlaces entrantes atraerá más enlaces entrantes que una página normal. Esto genera una ley de potencia, pero el gráfico resultante difiere del gráfico web real en otras propiedades, como la presencia de pequeñas comunidades estrechamente conectadas. Se han propuesto y estudiado modelos y características de red más generales. Por ejemplo, Pachon et al. (2018) propusieron una variante del modelo generativo de los ricos se hacen más ricos que tiene en cuenta dos reglas de unión diferentes: un mecanismo de unión preferencial y una elección uniforme solo para los nodos más recientes. ^[27] Para una revisión, consulte el libro de Dorogovtsev y Mendes . ^{[ cita requerida ]} Algunos mecanismos, como la unión preferencial superlineal y la unión del segundo vecino, generan redes que son transitoriamente libres de escala, pero se desvían de una ley de potencia a medida que las redes crecen. ^{[7] [8]}

Pennock et al. (2002) propusieron un modelo generativo algo diferente para los enlaces web. Examinaron comunidades con intereses en un tema específico, como las páginas de inicio de universidades, empresas públicas, periódicos o científicos, y descartaron los principales centros de la Web. En este caso, la distribución de enlaces ya no era una ley de potencia, sino que se parecía a una distribución normal . Basándose en estas observaciones, los autores propusieron un modelo generativo que combina el apego preferencial con una probabilidad base de obtener un enlace.

Otro modelo generativo es el modelo de copia estudiado por Kumar et al. ^[28] (2000), en el que los nuevos nodos eligen un nodo existente al azar y copian una fracción de los enlaces del nodo existente. Esto también genera una ley de potencia.

Hay dos componentes principales que explican la aparición de la distribución de ley de potencia en el modelo de Barabási-Albert : el crecimiento y la adhesión preferencial. ^[29] Por "crecimiento" se entiende un proceso de crecimiento en el que, durante un período prolongado de tiempo, nuevos nodos se unen a un sistema ya existente, una red (como la World Wide Web, que ha crecido en miles de millones de páginas web en 10 años). Finalmente, por "adhesión preferencial" se entiende que los nuevos nodos prefieren conectarse a nodos que ya tienen un gran número de enlaces con otros. Por lo tanto, existe una mayor probabilidad de que cada vez más nodos se enlacen con aquel que ya tiene muchos enlaces, lo que lleva a este nodo a un nodo in fine . ^[9] Dependiendo de la red, los nodos pueden ser assortativos o disassortativos. La assortatividad se encontraría en redes sociales en las que las personas bien conectadas/famosas tenderían a conocerse mejor entre sí. La disassortatividad se encontraría en redes tecnológicas (Internet, World Wide Web) y biológicas (interacción de proteínas, metabolismo). ^[29]

Sin embargo, el crecimiento de las redes (añadir nuevos nodos) no es una condición necesaria para crear una red libre de escala (véase Dangalchev ^[30] ). Una posibilidad (Caldarelli et al. 2002) es considerar la estructura como estática y trazar un vínculo entre los vértices de acuerdo con una propiedad particular de los dos vértices involucrados. Una vez especificada la distribución estadística para estas propiedades de los vértices (aptitud), resulta que en algunas circunstancias también las redes estáticas desarrollan propiedades libres de escala.

Modelo generalizado sin escala

Se ha producido un gran auge en el modelado de redes complejas sin escala . La receta de Barabási y Albert ^[31] ha sido seguida por varias variaciones y generalizaciones ^{[32] [33] [34] [35] [27]} y la renovación de trabajos matemáticos previos. ^[36]

En términos actuales, si una red compleja tiene una distribución de ley de potencia de cualquiera de sus métricas, generalmente se considera una red libre de escala. De manera similar, cualquier modelo con esta característica se denomina modelo libre de escala. ^[17]

Características

Muchas redes reales son (aproximadamente) libres de escala y, por lo tanto, requieren modelos libres de escala para describirlas. En el esquema de Price, se necesitan dos ingredientes para construir un modelo libre de escala:

1. Agregar o quitar nodos . Normalmente nos concentramos en hacer crecer la red, es decir, agregar nodos.

2. Conexión preferencial : Es la probabilidad de que nuevos nodos se conecten al nodo “antiguo”. ${\displaystyle \Pi }$

Cabe señalar que algunos modelos (véase Dangalchev ^[30] y el modelo Fitness a continuación) también pueden funcionar de forma estática, sin cambiar el número de nodos. También debe tenerse en cuenta que el hecho de que los modelos de "fijación preferencial" den lugar a redes sin escala no demuestra que este sea el mecanismo subyacente a la evolución de las redes sin escala del mundo real, ya que podrían existir diferentes mecanismos en funcionamiento en sistemas del mundo real que, no obstante, den lugar a la escala.

Ejemplos

Se han hecho varios intentos de generar propiedades de red sin escala. A continuación, se muestran algunos ejemplos:

El modelo Barabási-Albert

El modelo de Barabási-Albert , una versión no dirigida del modelo de Price, tiene una conexión preferencial lineal y agrega un nuevo nodo en cada paso de tiempo. ${\displaystyle \Pi (k_{i})={\frac {k_{i}}{\sum _{j}k_{j}}}}$

(Nota: otra característica general de en redes reales es que , es decir, existe una probabilidad distinta de cero de que un nuevo nodo se una a un nodo aislado. Por lo tanto, en general tiene la forma , donde es el atractivo inicial del nodo). ${\displaystyle \Pi (k)}$ ${\displaystyle \Pi (0)\neq 0}$ ${\displaystyle \Pi (k)}$ ${\displaystyle \Pi (k)=A+k^{\alpha }}$ ${\displaystyle A}$

Modelo de red de dos niveles

Dangalchev (ver ^[30] ) construye un modelo 2-L considerando la importancia de cada uno de los vecinos de un nodo objetivo en la vinculación preferencial. El atractivo de un nodo en el modelo 2-L depende no solo del número de nodos vinculados a él, sino también del número de vínculos en cada uno de estos nodos.

${\displaystyle \Pi (k_{i})={\frac {k_{i}+C\sum _{(i,j)}k_{j}}{\sum _{j}k_{j}+C\sum _{j}k_{j}^{2}}},}$

donde C es un coeficiente entre 0 y 1.

Una variante del modelo 2-L, el modelo k2, en el que los nodos vecinos primero y segundo contribuyen por igual al atractivo de un nodo objetivo, demuestra la aparición de redes transitorias sin escala. ^[8] En el modelo k2, la distribución de grados parece aproximadamente sin escala mientras la red sea relativamente pequeña, pero surgen desviaciones significativas del régimen sin escala a medida que la red se hace más grande. Esto da como resultado que el atractivo relativo de los nodos con diferentes grados cambie con el tiempo, una característica que también se observa en redes reales.

Modelo de apego impulsado por la mediación (MDA)

En el modelo de conexión impulsado por mediación (MDA) , un nuevo nodo que viene con aristas elige un nodo conectado existente al azar y luego se conecta a sí mismo, no con ese, sino con uno de sus vecinos, también elegidos al azar. La probabilidad de que el nodo del nodo existente elegido sea ${\displaystyle m}$ ${\displaystyle m}$ ${\displaystyle \Pi (i)}$ ${\displaystyle i}$

${\displaystyle \Pi (i)={\frac {k_{i}}{N}}{\frac {\sum _{j=1}^{k_{i}}{\frac {1}{k_{j}}}}{k_{i}}}.}$

El factor es el inverso de la media armónica (IHM) de los grados de los vecinos de un nodo . Una extensa investigación numérica sugiere que, aproximadamente, el valor medio de IHM en el límite grande se convierte en una constante, lo que significa que . Esto implica que cuanto mayores sean los enlaces (grado) que tenga un nodo, mayor será su probabilidad de obtener más enlaces, ya que se puede llegar a ellos de una mayor cantidad de formas a través de mediadores, lo que esencialmente encarna la idea intuitiva del mecanismo de los ricos se hacen más ricos (o la regla de unión preferencial del modelo de Barabasi-Albert). Por lo tanto, se puede ver que la red MDA sigue la regla de PA, pero disfrazada. ^[37] ${\displaystyle {\frac {\sum _{j=1}^{k_{i}}{\frac {1}{k_{j}}}}{k_{i}}}}$ ${\displaystyle k_{i}}$ ${\displaystyle i}$ ${\displaystyle m>14}$ ${\displaystyle N}$ ${\displaystyle \Pi (i)\propto k_{i}}$

Sin embargo, como se describe el mecanismo del ganador se lo lleva todo, vemos que casi el total de nodos tiene grado uno y uno es súper rico en grado. A medida que el valor aumenta, la disparidad entre los súper ricos y los pobres disminuye y encontramos una transición del mecanismo de los ricos que se vuelven súper ricos al de los ricos que se vuelven más ricos. ${\displaystyle m=1}$ ${\displaystyle 99\%}$ ${\displaystyle m}$ ${\displaystyle m>14}$

Fijación preferencial no lineal

El modelo de Barabási–Albert supone que la probabilidad de que un nodo se una a otro nodo es proporcional al grado de nodo . Esta suposición implica dos hipótesis: primero, que depende de , en contraste con los grafos aleatorios en los que , y segundo, que la forma funcional de es lineal en . ${\displaystyle \Pi (k)}$ ${\displaystyle i}$ ${\displaystyle k}$ ${\displaystyle i}$ ${\displaystyle \Pi (k)}$ ${\displaystyle k}$ ${\displaystyle \Pi (k)=p}$ ${\displaystyle \Pi (k)}$ ${\displaystyle k}$

En el apego preferencial no lineal, la forma de no es lineal, y estudios recientes han demostrado que la distribución de grados depende en gran medida de la forma de la función. ${\displaystyle \Pi (k)}$ ${\displaystyle \Pi (k)}$

Krapivsky, Redner y Leyvraz ^[34] demuestran que la naturaleza libre de escala de la red se destruye para la unión preferencial no lineal. El único caso en el que la topología de la red es libre de escala es aquel en el que la unión preferencial es asintóticamente lineal, es decir, como . En este caso, la ecuación de velocidad conduce a ${\displaystyle \Pi (k_{i})\sim a_{\infty }k_{i}}$ ${\displaystyle k_{i}\to \infty }$

${\displaystyle P(k)\sim k^{-\gamma }{\text{ with }}\gamma =1+{\frac {\mu }{a_{\infty }}}.}$

De esta manera, el exponente de la distribución de grados se puede ajustar a cualquier valor entre 2 y . ^{[ aclaración necesaria ]} ${\displaystyle \infty }$

Modelo de red jerárquica

Los modelos de redes jerárquicas son, por diseño, libres de escala y tienen una alta agrupación de nodos. ^[38]

La construcción iterativa conduce a una red jerárquica. Partiendo de un clúster completamente conectado de cinco nodos, creamos cuatro réplicas idénticas que conectan los nodos periféricos de cada clúster al nodo central del clúster original. A partir de esto, obtenemos una red de 25 nodos ( N  = 25). Repitiendo el mismo proceso, podemos crear cuatro réplicas más del clúster original: los cuatro nodos periféricos de cada uno se conectan al nodo central de los nodos creados en el primer paso. Esto da N  = 125, y el proceso puede continuar indefinidamente.

Modelo de fitness

La idea es que el vínculo entre dos vértices no se asigna aleatoriamente con una probabilidad p igual para todo el par de vértices, sino que para cada vértice j hay una aptitud intrínseca x _j y se crea un vínculo entre el vértice i y j con una probabilidad . ^[39] En el caso de World Trade Web es posible reconstruir todas las propiedades utilizando como aptitudes del país su PIB y tomando ${\displaystyle p(x_{i},x_{j})}$

${\displaystyle p(x_{i},x_{j})={\frac {\delta x_{i}x_{j}}{1+\delta x_{i}x_{j}}}.}$^[40]

Gráficas geométricas hiperbólicas

Suponiendo que una red tiene una geometría hiperbólica subyacente, se puede utilizar el marco de las redes espaciales para generar distribuciones de grados libres de escala. Esta distribución de grados heterogénea simplemente refleja la curvatura negativa y las propiedades métricas de la geometría hiperbólica subyacente. ^[41]

Transformación dual de aristas para generar gráficos libres de escala con las propiedades deseadas

A partir de gráficos libres de escala con correlación de grado bajo y coeficiente de agrupamiento, se pueden generar nuevos gráficos con correlaciones de grado mucho más altos y coeficientes de agrupamiento mediante la aplicación de la transformación dual de aristas. ^[19]

Modelo de vinculación preferencial uniforme (modelo UPA)

El modelo UPA es una variante del modelo de apego preferencial (propuesto por Pachon et al.) que tiene en cuenta dos reglas de apego diferentes: un mecanismo de apego preferencial (con probabilidad 1−p) que enfatiza el sistema de los ricos se hacen más ricos, y una elección uniforme (con probabilidad p) para los nodos más recientes. Esta modificación es interesante para estudiar la robustez del comportamiento libre de escala de la distribución de grados. Se demuestra analíticamente que la distribución de grados asintóticamente de ley de potencia se conserva. ^[27]

Redes ideales sin escala

En el contexto de la teoría de redes, una red ideal libre de escala es una red aleatoria con una distribución de grados que sigue la distribución de densidad de gas ideal libre de escala . Estas redes son capaces de reproducir distribuciones de tamaño de ciudad y resultados electorales desentrañando la distribución de tamaño de los grupos sociales con la teoría de la información sobre redes complejas cuando se aplica un proceso de crecimiento de clúster competitivo a la red. ^{[42] [43]} En modelos de redes ideales libres de escala es posible demostrar que el número de Dunbar es la causa del fenómeno conocido como los ' seis grados de separación '.

Características novedosas

Para una red libre de escala con nodos y exponente de ley de potencia , el subgrafo inducido construido por vértices con grados mayores que es una red libre de escala con , casi con seguridad . ^[44] ${\displaystyle n}$ ${\displaystyle \gamma >3}$ ${\displaystyle \log {n}\times \log ^{*}{n}}$ ${\displaystyle \gamma '=2}$

Estimación del exponente de la ley de potencia

La estimación del exponente de la ley de potencia de una red libre de escala se realiza típicamente utilizando la estimación de máxima verosimilitud con los grados de unos pocos nodos muestreados uniformemente. ^[3] Sin embargo, dado que el muestreo uniforme no obtiene suficientes muestras de la importante cola pesada de la distribución de grados de la ley de potencia, este método puede producir un sesgo grande y una varianza. Recientemente se ha propuesto muestrear amigos aleatorios (es decir, extremos aleatorios de enlaces aleatorios) que tienen más probabilidades de provenir de la cola de la distribución de grados como resultado de la paradoja de la amistad . ^{[45] [46]} Teóricamente, la estimación de máxima verosimilitud con amigos aleatorios conduce a un sesgo menor y una varianza menor en comparación con el enfoque clásico basado en el muestreo uniforme. ^[46] ${\displaystyle \gamma }$

Véase también

• Gráfico aleatorio  : gráfico generado por un proceso aleatorio
• Modelo Erdős-Rényi  : dos modelos estrechamente relacionados para generar gráficos aleatorios
• Fijación preferencial no lineal
• Condensación de Bose-Einstein (teoría de redes)  : un modelo en la ciencia de redesPages displaying wikidata descriptions as a fallback
• Invariancia de escala  : características que no cambian si las escalas de longitud o energía se multiplican por un factor común
• Red compleja  : red con características topológicas no triviales
• Webgraph  – Gráfico de páginas web conectadas
• Modelo Barabási-Albert  : algoritmo de generación de redes sin escala
• Modelo Bianconi-Barabási  - modelo en ciencia de redesPages displaying wikidata descriptions as a fallback

Referencias

1. Onnela, J.-P.; Saramaki, J.; Hyvonen, J.; Szabo, G.; Lazer, D.; Kaski, K.; Kertesz, J.; Barabasi, A. -L. (2007). "Estructura y fortalezas de los enlaces en redes de comunicación móvil". Actas de la Academia Nacional de Ciencias . 104 (18): 7332–7336. arXiv : physics/0610104 . Bibcode :2007PNAS..104.7332O. doi : 10.1073/pnas.0610245104 . PMC  1863470. PMID  17456605 .
2. Choromański, K.; Matuszak, M.; MiȩKisz, J. (2013). "Gráfico libre de escala con fijación preferencial y estructura de vértice interna evolutiva". Revista de física estadística . 151 (6): 1175–1183. Código Bibliográfico :2013JSP...151.1175C. doi : 10.1007/s10955-013-0749-1 .
3. Clauset, Aaron; Cosma Rohilla Shalizi; ME J Newman (2009). "Distribuciones de ley de potencia en datos empíricos". SIAM Review . 51 (4): 661–703. arXiv : 0706.1062 . Código Bibliográfico :2009SIAMR..51..661C. doi :10.1137/070710111. S2CID  9155618.
4. Broido, Anna; Aaron Clauset (4 de marzo de 2019). "Las redes sin escala son raras". Nature Communications . 10 (1): 1017. arXiv : 1801.03400 . Bibcode :2019NatCo..10.1017B. doi :10.1038/s41467-019-08746-5. PMC 6399239 . PMID  30833554. 
5. Holme, Petter (diciembre de 2019). «Raro y omnipresente: perspectivas sobre redes sin escala». Nature Communications . 10 (1): 1016. Bibcode :2019NatCo..10.1016H. doi : 10.1038/s41467-019-09038-8 . PMC 6399274 . PMID  30833568. 
6. Stumpf, MPH; Porter, MA (10 de febrero de 2012). "Verdades críticas sobre las leyes de potencia". Science . 335 (6069): 665–666. Bibcode :2012Sci...335..665S. doi :10.1126/science.1216142. PMID  22323807. S2CID  206538568.
7. Krapivsky, Paul; Krioukov, Dmitri (21 de agosto de 2008). "Redes libres de escala como regímenes preasintóticos de unión preferencial superlineal". Physical Review E . 78 (2): 026114. arXiv : 0804.1366 . Bibcode :2008PhRvE..78b6114K. doi :10.1103/PhysRevE.78.026114. PMID  18850904. S2CID  14292535.
8. Falkenberg, Max; Lee, Jong-Hyeok; Amano, Shun-ichi; Ogawa, Ken-ichiro; Yano, Kazuo; Miyake, Yoshihiro; Evans, Tim S.; Christensen, Kim (18 de junio de 2020). "Identificación de la dependencia del tiempo en el crecimiento de la red". Physical Review Research . 2 (2): 023352. arXiv : 2001.09118 . doi : 10.1103 / PhysRevResearch.2.023352 .
9. Barabási, Albert-László ; Alberto, Réka. (15 de octubre de 1999). "Aparición del escalado en redes aleatorias". Ciencia . 286 (5439): 509–512. arXiv : cond-mat/9910332 . Código Bib : 1999 Ciencia... 286.. 509B. doi : 10.1126/ciencia.286.5439.509. SEÑOR  2091634. PMID  10521342. S2CID  524106.
10. Entre los siete ejemplos estudiados por Amaral et al, seis de ellos eran de escala única y solo el ejemplo iii , la red de actores de películas tenía un régimen de ley de potencia seguido de un corte brusco. Ninguno de los ejemplos de Amaral et al obedeció el régimen de ley de potencia para k grande , es decir, ninguno de estos siete ejemplos demostró ser libre de escala. Véase especialmente el comienzo de la sección de discusión de Amaral LAN, Scala A, Barthelemy M, Stanley HE (2000). "Clases de redes de mundo pequeño". PNAS . 97 (21): 11149–52. arXiv : cond-mat/0001458 . Bibcode :2000PNAS...9711149A. doi : 10.1073/pnas.200327197 . PMC 17168 . PMID  11005838. 
11. Dorogovtsev, S.; Mendes, J.; Samukhin, A. (2000). "Estructura de redes en crecimiento con enlaces preferenciales". Physical Review Letters . 85 (21): 4633–4636. arXiv : cond-mat/0004434 . Código Bibliográfico :2000PhRvL..85.4633D. doi :10.1103/PhysRevLett.85.4633. PMID  11082614. S2CID  118876189.
12. Bollobás, B. ; Riordan, O.; Spencer, J.; Tusnády, G. (2001). "La secuencia de grados de un proceso de grafo aleatorio sin escala". Estructuras y algoritmos aleatorios . 18 (3): 279–290. doi :10.1002/rsa.1009. MR  1824277. S2CID  1486779.
13. Dorogovtsev, SN; Mendes, JFF (2002). "Evolución de las redes". Avances en Física . 51 (4): 1079–1187. arXiv : cond-mat/0106144 . Código Bibliográfico :2002AdPhy..51.1079D. doi :10.1080/00018730110112519. S2CID  429546.
14. Willinger, Walter; David Alderson; John C. Doyle (mayo de 2009). «Matemáticas e Internet: una fuente de enorme confusión y gran potencial» (PDF) . Avisos de la AMS . 56 (5). American Mathematical Society: 586–599. Archivado (PDF) desde el original el 15 de mayo de 2011. Consultado el 3 de febrero de 2011 .
15. Itzykson, Claude; Drouffe, Jean-Michel (1989). Teoría estadística de campos: volumen 1, del movimiento browniano a la renormalización y la teoría de calibración reticular (1.ª ed.). Nueva York: Cambridge University Press. ISBN 978-0-521-34058-8.
16. Itzykson, Claude; Drouffe, Jean-Michel (1989). Teoría estadística de campos: volumen 2, acoplamiento fuerte, métodos de Monte Carlo, teoría de campos conforme y sistemas aleatorios (1.ª ed.). Nueva York: Cambridge University Press. ISBN 978-0-521-37012-7.
17. Meng, Xiangyi; Zhou, Bin (2023). "Redes sin escala más allá de la distribución de grados de ley de potencia". Caos, solitones y fractales . 176 : 114173. arXiv : 2310.08110 . Código Bibliográfico :2023CSF...17614173M. doi :10.1016/j.chaos.2023.114173. S2CID  263909425.
18. Tanaka, Reiko (2005). "Redes metabólicas de gran escala". Phys. Rev. Lett . 94 (16): 168101. Bibcode :2005PhRvL..94p8101T. doi :10.1103/PhysRevLett.94.168101. PMID  15904266.
19. Ramezanpour, A.; Karimipour, V.; Mashaghi, A. (2003). "Generación de redes correlacionadas a partir de redes no correlacionadas". Phys. Rev. E . 67 (4): 046107. arXiv : cond-mat/0212469 . Código Bibliográfico :2003PhRvE..67d6107R. doi :10.1103/PhysRevE.67.046107. PMID  12786436. S2CID  33054818.
20. De Masi, Giulia; et al. (2006). "Modelo de aptitud para el mercado monetario interbancario italiano". Physical Review E . 74 (6): 066112. arXiv : physics/0610108 . Bibcode :2006PhRvE..74f6112D. doi :10.1103/PhysRevE.74.066112. PMID  17280126. S2CID  30814484.
21. Soramäki, Kimmo; et al. (2007). "La topología de los flujos de pago interbancarios". Physica A: Mecánica estadística y sus aplicaciones . 379 (1): 317–333. Bibcode :2007PhyA..379..317S. doi :10.1016/j.physa.2006.11.093. hdl : 10419/60649 .
22. Steyvers, Mark; Joshua B. Tenenbaum (2005). "La estructura a gran escala de las redes semánticas: análisis estadísticos y un modelo de crecimiento semántico". Ciencia cognitiva . 29 (1): 41–78. arXiv : cond-mat/0110012 . doi :10.1207/s15516709cog2901_3. PMID  21702767. S2CID  6000627.
23. Fratini, Michela; Poccia, Nicola; Ricci, Alejandro; Campi, Gaetano; Burghammer, Manfred; Aeppli, Gabriel; Bianconi, Antonio (2010). "Organización estructural libre de escala de intersticiales de oxígeno en La2CuO4+y". Naturaleza . 466 (7308): 841–4. arXiv : 1008.2015 . Código Bib :2010Natur.466..841F. doi : 10.1038/naturaleza09260. PMID  20703301. S2CID  4405620.
24. Poccia, Nicola; Ricci, Alejandro; Campi, Gaetano; Fratini, Michela; Puri, Alejandro; Di Gioacchino, Daniele; Marcelli, Augusto; Reynolds, Michael; Burghammer, Manfred; Saini, Naurang L.; Aeppli, Gabriel; Bianconi, Antonio (2012). "Óptima falta de homogeneidad de las distorsiones de la red local en La2CuO4 + y". PNAS . 109 (39): 15685–15690. arXiv : 1208.0101 . Código bibliográfico : 2012PNAS..10915685P. doi : 10.1073/pnas.1208492109 . PMC 3465392 . PMID  22961255. 
25. Hassan, MK; Hassan, MZ; Pavel, NI (2010). "Topología de red libre de escala y multifractalidad en una red estocástica plana ponderada". New Journal of Physics . 12 (9): 093045. arXiv : 1008.4994 . Bibcode :2010NJPh...12i3045H. doi : 10.1088/1367-2630/12/9/093045 .
26. Hassan, MK; Hassan, MZ; Pavel, NI (2010). "Desorden del número de coordinación sin escala y desorden del tamaño multifractal en red estocástica planar ponderada". J. Phys.: Conf. Ser . 297 : 01.
27. Pachon, Angelica; Sacerdote, Laura; Yang, Shuyi (2018). "Comportamiento libre de escala de redes con copresencia de reglas de unión preferencial y uniforme". Physica D: Nonlinear Phenomena . 371 : 1–12. arXiv : 1704.08597 . Bibcode :2018PhyD..371....1P. doi :10.1016/j.physd.2018.01.005. S2CID  119320331.
28. Kumar, Ravi; Raghavan, Prabhakar (2000). Modelos estocásticos para el gráfico web (PDF) . Fundamentos de la informática, 41.º simposio anual sobre. págs. 57–65. doi :10.1109/SFCS.2000.892065. Archivado (PDF) desde el original el 3 de marzo de 2016. Consultado el 10 de febrero de 2016 .
29. Barabási, Albert-László ; Zoltán N., Oltvai. (2004). "Biología de redes: comprensión de la organización funcional de la célula". Naturaleza Reseñas Genética . 5 (2): 101-113. doi :10.1038/nrg1272. PMID  14735121. S2CID  10950726.
30. Dangalchev, Chavdar (julio de 2004). "Modelos de generación para redes libres de escala". Physica A: Mecánica estadística y sus aplicaciones . 338 (3–4): 659–671. Bibcode :2004PhyA..338..659D. doi :10.1016/j.physa.2004.01.056.
31. Barabási, A.-L. y R. Albert, Science 286 , 509 (1999).
32. R. Albert y AL Barabási, Phys. Rev. Lett. 85 , 5234 (2000).
33. SN Dorogovtsev, JFF Mendes y AN Samukhim, cond-mat/0011115.
34. PL Krapivsky, S. Redner y F. Leyvraz, Phys. Rev. Lett. 85 , 4629 (2000).
35. B. Tadic, Física A 293 , 273(2001).
36. S. Bomholdt y H. Ebel, cond-mat/0008465; HA Simon, Bimetrika 42 , 425 (1955).
37. Hassan, MK; Islam, Liana; Arefinul Haque, Syed (2017). "Distribución de grados, distribución de tamaño de rango y persistencia del liderazgo en redes de apego impulsadas por la mediación". Physica A . 469 : 23–30. arXiv : 1411.3444 . Bibcode :2017PhyA..469...23H. doi :10.1016/j.physa.2016.11.001. S2CID  51976352.
38. Ravasz, E.; Barabási (2003). "Organización jerárquica en redes complejas". Física. Rev. E. 67 (2): 026112. arXiv : cond-mat/0206130 . Código bibliográfico : 2003PhRvE..67b6112R. doi :10.1103/physreve.67.026112. PMID  12636753. S2CID  17777155.
39. Caldarelli, G.; et al. (2002). "Redes libres de escala a partir de aptitud intrínseca de vértices variables" (PDF) . Phys. Rev. Lett . 89 (25): 258702. Bibcode :2002PhRvL..89y8702C. doi :10.1103/physrevlett.89.258702. PMID  12484927.
40. Garlaschelli, D.; et al. (2004). "Propiedades topológicas dependientes de la aptitud de la red de comercio mundial". Phys. Rev. Lett . 93 (18): 188701. arXiv : cond-mat/0403051 . Código Bibliográfico :2004PhRvL..93r8701G. doi :10.1103/physrevlett.93.188701. PMID  15525215. S2CID  16367275.
41. Krioukov, Dmitri; Papadopoulos, Fragkiskos; Kitsak, Maksim; Vahdat, Amin; Boguñá, Marián (2010). "Geometría hiperbólica de redes complejas". Revisión física E. 82 (3): 036106. arXiv : 1006.5169 . Código bibliográfico : 2010PhRvE..82c6106K. doi : 10.1103/PhysRevE.82.036106. PMID  21230138. S2CID  6451908.
42. A. Hernando; D. Villuendas; C. Vesperinas; M. Abad; A. Plastino (2009). "Descifrando la distribución del tamaño de los grupos sociales con la teoría de la información en redes complejas". arXiv : 0905.3704 [physics.soc-ph]., enviado al European Physical Journal B
43. André A. Moreira; Demétrius R. Paula; Raimundo N. Costa Filho; José S. Andrade, Jr. (2006). "Crecimiento competitivo de clusters en redes complejas". Revisión física E. 73 (6): 065101. arXiv : cond-mat/0603272 . Código bibliográfico : 2006PhRvE..73f5101M. doi : 10.1103/PhysRevE.73.065101. PMID  16906890. S2CID  45651735.
44. Heydari, H.; Taheri, SM; Kaveh, K. (2018). "Conjunto independiente máximo distribuido en redes sin escala". arXiv : 1804.02513 [cs.DC].
45. Eom, Young-Ho; Jo, Hang-Hyun (11 de mayo de 2015). "Tail-scope: Uso de amigos para estimar colas pesadas de distribuciones de grado en redes complejas a gran escala". Scientific Reports . 5 (1): 9752. arXiv : 1411.6871 . Bibcode :2015NatSR...5E9752E. doi : 10.1038/srep09752 . ISSN  2045-2322. PMC 4426729 . PMID  25959097. 
46. Nettasinghe, Buddhika; Krishnamurthy, Vikram (19 de mayo de 2021). "Estimación de máxima verosimilitud de distribuciones de grados de ley de potencia mediante muestreo basado en la paradoja de la amistad". ACM Transactions on Knowledge Discovery from Data . 15 (6): 1–28. arXiv : 1908.00310 . doi : 10.1145/3451166 . ISSN  1556-4681.

Lectura adicional

• Albert R.; Barabási A.-L. (2002). "Mecánica estadística de redes complejas". Rev. Mod. Phys . 74 (1): 47–97. arXiv : cond-mat/0106096 . Código Bibliográfico :2002RvMP...74...47A. doi :10.1103/RevModPhys.74.47. S2CID  60545.
• Amaral LAN, Scala A, Barthelemy M, Stanley HE (2000). "Clases de redes de mundo pequeño". PNAS . 97 (21): 11149–52. arXiv : cond-mat/0001458 . Bibcode :2000PNAS...9711149A. doi : 10.1073/pnas.200327197 . PMC  17168 . PMID  11005838.
• Barabási, Albert-László (2004). Vinculado: Cómo todo está conectado con todo lo demás . Pub Perseo. ISBN 0-452-28439-2.
• Barabási, Albert-László; Bonabeau, Eric (mayo de 2003). "Redes sin escala" (PDF) . Científico americano . 288 (5): 50–9. Código Bib : 2003SciAm.288e..60B. doi : 10.1038/scientificamerican0503-60. PMID  12701331.
• Dan Braha; Yaneer Bar-Yam (2004). "Topología de redes de resolución de problemas de ingeniería a gran escala" (PDF) . Phys. Rev. E . 69 (1): 016113. Bibcode :2004PhRvE..69a6113B. doi :10.1103/PhysRevE.69.016113. PMID  14995673. S2CID  1001176.
• Caldarelli G. "Redes libres de escala" Oxford University Press, Oxford (2007).
• Caldarelli G.; Capocci A.; De Los Rios P.; Muñoz MA (2002). "Redes libres de escala a partir de aptitud intrínseca de vértices variables". Physical Review Letters . 89 (25): 258702. arXiv : cond-mat/0207366 . Bibcode :2002PhRvL..89y8702C. doi :10.1103/PhysRevLett.89.258702. PMID  12484927.
• Dangalchev, Ch. (2004). "Modelos de generación para redes sin escala". Physica A . 338 (3–4): 659–671. Bibcode :2004PhyA..338..659D. doi :10.1016/j.physa.2004.01.056.
• Dorogovtsev, SN; Mendes, JFF; Samukhin, AN (2000). "Estructura de redes en crecimiento: solución exacta del modelo de Barabási—Albert". Phys. Rev. Lett . 85 (21): 4633–6. arXiv : cond-mat/0004434 . Código Bibliográfico :2000PhRvL..85.4633D. doi :10.1103/PhysRevLett.85.4633. PMID  11082614. S2CID  118876189.
• Dorogovtsev, SN; Mendes, JFF (2003). Evolución de las redes: desde las redes biológicas hasta Internet y la WWW . Oxford University Press. ISBN 0-19-851590-1.
• Dorogovtsev, SN; Goltsev AV; Mendes, JFF (2008). "Fenómenos críticos en redes complejas". Rev. Mod. Phys . 80 (4): 1275–1335. arXiv : 0705.0010 . Bibcode :2008RvMP...80.1275D. doi :10.1103/RevModPhys.80.1275. S2CID  3174463.
• Dorogovtsev, SN; Mendes, JFF (2002). "Evolución de las redes". Avances en Física . 51 (4): 1079–1187. arXiv : cond-mat/0106144 . Código Bibliográfico :2002AdPhy..51.1079D. doi :10.1080/00018730110112519. S2CID  429546.
• Erdős, P. ; Rényi, A. (1960). Sobre la evolución de grafos aleatorios (PDF) . Vol. 5. Publicación del Instituto de Matemáticas de la Academia Húngara de Ciencias. pp. 17–61.
• Faloutsos, M.; Faloutsos, P.; Faloutsos, C. (1999). "Sobre las relaciones de ley de potencia de la topología de Internet". Comp. Comm. Rev. 29 ( 4): 251–262. doi :10.1145/316194.316229.
• Li, L.; Alderson, D.; Tanaka, R.; Doyle, JC; Willinger, W. (2005). "Hacia una teoría de grafos libres de escala: definición, propiedades e implicaciones (versión extendida)". arXiv : cond-mat/0501169 .
• Kumar, R.; Raghavan, P.; Rajagopalan, S.; Sivakumar, D.; Tomkins, A.; Upfal, E. (2000). "Modelos estocásticos para el gráfico web" (PDF) . Actas del 41.º Simposio anual sobre fundamentos de la informática (FOCS) . Redondo Beach, CA: IEEE CS Press. págs. 57–65.
• Matlis, Jan (4 de noviembre de 2002). "Redes sin escala".
• Newman, Mark EJ (2003). "La estructura y función de redes complejas". SIAM Review . 45 (2): 167–256. arXiv : cond-mat/0303516 . Código Bibliográfico :2003SIAMR..45..167N. doi :10.1137/S003614450342480. S2CID  221278130.
• Pastor-Satorras, R.; Vespignani, A. (2004). Evolución y estructura de Internet: un enfoque de física estadística . Cambridge University Press. ISBN 0-521-82698-5.
• Pennock, DM; Flake, GW; Lawrence, S.; Glover, EJ; Giles, CL (2002). "Los ganadores no se llevan todo: caracterización de la competencia por los enlaces en la Web". PNAS . 99 (8): 5207–11. Bibcode :2002PNAS...99.5207P. doi : 10.1073/pnas.032085699 . PMC  122747 . PMID  16578867.
• Robb, John. Redes libres de escala y terrorismo, 2004.
• Keller, EF (2005). "Revisiting 'scale-free' networks". BioEssays . 27 (10): 1060–8. doi :10.1002/bies.20294. PMID  16163729. Archivado desde el original el 13 de agosto de 2011.
• Onody, RN; de Castro, PA (2004). "Estudio de redes complejas en futbolistas brasileños". Phys. Rev. E . 70 (3): 037103. arXiv : cond-mat/0409609 . Bibcode :2004PhRvE..70c7103O. doi :10.1103/PhysRevE.70.037103. PMID  15524675. S2CID  31653489.
• Kasthurirathna, D.; Piraveenan, M. (2015). "Estudio de redes complejas de jugadores de fútbol brasileños". Sci. Rep . En prensa.