Cinemática inversa

Cálculo de valores articulares de una cadena cinemática a partir de una posición final conocida

Cinemática directa vs. cinemática inversa

En animación por computadora y robótica , la cinemática inversa es el proceso matemático de calcular los parámetros articulares variables necesarios para colocar el extremo de una cadena cinemática , como un manipulador de robot o el esqueleto de un personaje de animación , en una posición y orientación determinadas en relación con el inicio de la cadena. Dados los parámetros articulares, la posición y orientación del extremo de la cadena, por ejemplo, la mano del personaje o robot, normalmente se pueden calcular directamente utilizando múltiples aplicaciones de fórmulas trigonométricas, un proceso conocido como cinemática directa . Sin embargo, la operación inversa es, en general, mucho más desafiante. ^{[1] [2] [3]}

La cinemática inversa también se utiliza para recuperar los movimientos de un objeto del mundo a partir de otros datos, como una película de esos movimientos o una película del mundo tal como lo ve una cámara que realiza esos movimientos. Esto ocurre, por ejemplo, cuando los movimientos filmados de un actor humano deben ser duplicados por un personaje animado .

Robótica

En robótica, la cinemática inversa hace uso de las ecuaciones cinemáticas para determinar los parámetros de las articulaciones que proporcionan una configuración deseada (posición y rotación) para cada uno de los efectores finales del robot . ^[4] Esto es importante porque las tareas del robot se realizan con los efectores finales, mientras que el esfuerzo de control se aplica a las articulaciones. Determinar el movimiento de un robot para que sus efectores finales se muevan desde una configuración inicial a una configuración deseada se conoce como planificación del movimiento . La cinemática inversa transforma el plan de movimiento en trayectorias de actuadores de articulaciones para el robot. ^[2] Fórmulas similares determinan las posiciones del esqueleto de un personaje animado que se moverá de una manera particular en una película, o de un vehículo como un automóvil o un bote que contiene la cámara que está filmando una escena de una película. Una vez que se conocen los movimientos de un vehículo, se pueden usar para determinar el punto de vista en constante cambio para imágenes generadas por computadora de objetos en el paisaje, como edificios, de modo que estos objetos cambien en perspectiva mientras que ellos mismos no parecen moverse cuando la cámara transportada por el vehículo pasa junto a ellos.

El movimiento de una cadena cinemática , ya sea un robot o un personaje animado, se modela mediante las ecuaciones cinemáticas de la cadena. Estas ecuaciones definen la configuración de la cadena en términos de sus parámetros de articulación. La cinemática directa utiliza los parámetros de articulación para calcular la configuración de la cadena, y la cinemática inversa invierte este cálculo para determinar los parámetros de articulación que logran una configuración deseada. ^{[5] [6] [7]}

Análisis cinemático

Un modelo del esqueleto humano como cadena cinemática permite el posicionamiento mediante cinemática inversa.

El análisis cinemático es uno de los primeros pasos en el diseño de la mayoría de los robots industriales. El análisis cinemático permite al diseñador obtener información sobre la posición de cada componente dentro del sistema mecánico. Esta información es necesaria para el posterior análisis dinámico junto con las rutas de control.

La cinemática inversa es un ejemplo del análisis cinemático de un sistema restringido de cuerpos rígidos, o cadena cinemática . Las ecuaciones cinemáticas de un robot se pueden utilizar para definir las ecuaciones de bucle de un sistema articulado complejo. Estas ecuaciones de bucle son restricciones no lineales sobre los parámetros de configuración del sistema. Los parámetros independientes en estas ecuaciones se conocen como grados de libertad del sistema.

Si bien existen soluciones analíticas al problema de la cinemática inversa para una amplia gama de cadenas cinemáticas, las herramientas de modelado y animación por computadora a menudo utilizan el método de Newton para resolver las ecuaciones cinemáticas no lineales. ^[2] Cuando se intenta encontrar una solución analítica, a menudo es conveniente explotar la geometría del sistema y descomponerlo utilizando subproblemas con soluciones conocidas . ^{[8] [9]}

Otras aplicaciones de los algoritmos cinemáticos inversos incluyen la manipulación interactiva, el control de la animación y la prevención de colisiones .

Cinemática inversa y animación 3D

La cinemática inversa es importante para la programación de juegos y la animación 3D , donde se utiliza para conectar físicamente a los personajes del juego con el mundo, como por ejemplo los pies que aterrizan firmemente sobre el terreno (consulte ^[10] para obtener un estudio completo sobre las técnicas de cinemática inversa en gráficos de computadora).

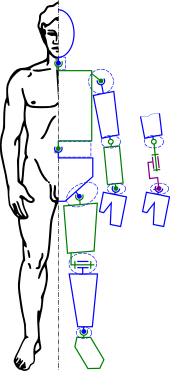
Una figura animada se modela con un esqueleto de segmentos rígidos conectados con articulaciones, llamado cadena cinemática . Las ecuaciones cinemáticas de la figura definen la relación entre los ángulos de las articulaciones de la figura y su pose o configuración. El problema de animación cinemática directa utiliza las ecuaciones cinemáticas para determinar la pose dados los ángulos de las articulaciones. El problema de cinemática inversa calcula los ángulos de las articulaciones para una pose deseada de la figura.

A menudo, a los diseñadores, artistas y animadores informáticos les resulta más fácil definir la configuración espacial de un conjunto o figura moviendo piezas, o brazos y piernas, en lugar de manipular directamente los ángulos de las articulaciones. Por lo tanto, la cinemática inversa se utiliza en sistemas de diseño asistido por ordenador para animar conjuntos y por artistas y animadores informáticos para posicionar figuras y personajes.

El conjunto se modela como enlaces rígidos conectados por articulaciones que se definen como relaciones de posición o restricciones geométricas. El movimiento de un elemento requiere el cálculo de los ángulos de las articulaciones de los otros elementos para mantener las restricciones de las articulaciones . Por ejemplo, la cinemática inversa permite a un artista mover la mano de un modelo humano en 3D a una posición y orientación deseadas y hacer que un algoritmo seleccione los ángulos adecuados de las articulaciones de la muñeca, el codo y el hombro. La implementación exitosa de la animación por computadora generalmente también requiere que la figura se mueva dentro de límites antropomórficos razonables.

Se puede definir un método para comparar la cinemática directa e inversa para la animación de un personaje en función de las ventajas inherentes a cada una. Por ejemplo, la animación por bloqueos en la que se utilizan grandes arcos de movimiento suele ser más ventajosa en la cinemática directa. Sin embargo, una animación más delicada y el posicionamiento del efector final objetivo en relación con otros modelos pueden resultar más sencillos utilizando la cinemática invertida. Los paquetes de creación digital (DCC) modernos ofrecen métodos para aplicar tanto la cinemática directa como la inversa a los modelos.

Soluciones analíticas a la cinemática inversa

En algunos casos, pero no en todos, existen soluciones analíticas para problemas cinemáticos inversos. Un ejemplo de ello es el de un robot de 6 grados de libertad (por ejemplo, 6 articulaciones giratorias) que se mueve en un espacio 3D (con 3 grados de libertad de posición y 3 grados de libertad de rotación). Si los grados de libertad del robot superan los grados de libertad del efector final, por ejemplo, con un robot de 7 grados de libertad con 7 articulaciones giratorias, entonces existen infinitas soluciones para el problema de cinemática inversa, y no existe una solución analítica. Ampliando aún más este ejemplo, es posible fijar una articulación y resolver analíticamente las otras articulaciones, pero tal vez se ofrezca una mejor solución mediante métodos numéricos (siguiente sección), que en cambio pueden optimizar una solución dadas las preferencias adicionales (costos en un problema de optimización).

Una solución analítica para un problema de cinemática inversa es una expresión de forma cerrada que toma la posición del efector final como entrada y proporciona las posiciones de las articulaciones como salida. Los solucionadores de cinemática inversa analíticos pueden ser significativamente más rápidos que los solucionadores numéricos y proporcionar más de una solución, pero solo un número finito de soluciones, para una determinada posición del efector final. ${\displaystyle q=f(x)}$

Muchos programas diferentes (como los programas FOSS IKFast y la biblioteca Inverse Kinematics Library) pueden resolver estos problemas de forma rápida y eficiente utilizando diferentes algoritmos, como el solucionador FABRIK. Un problema con estos solucionadores es que se sabe que no necesariamente brindan soluciones localmente uniformes entre dos configuraciones adyacentes, lo que puede causar inestabilidad si se requieren soluciones iterativas para la cinemática inversa, como si la IK se resolviera dentro de un bucle de control de alta velocidad.

Soluciones numéricas a problemas de CI

Existen muchos métodos para modelar y resolver problemas de cinemática inversa. Los métodos más flexibles suelen basarse en la optimización iterativa para buscar una solución aproximada, debido a la dificultad de invertir la ecuación de cinemática directa y la posibilidad de un espacio de solución vacío . La idea central detrás de varios de estos métodos es modelar la ecuación de cinemática directa utilizando una expansión en serie de Taylor , que puede ser más sencilla de invertir y resolver que el sistema original.

La técnica inversa jacobiana

La técnica inversa jacobiana es una forma simple pero efectiva de implementar la cinemática inversa. Sea variables que gobiernan la ecuación de cinemática directa, es decir, la función de posición. Estas variables pueden ser ángulos de articulación, longitudes u otros valores reales arbitrarios. Si, por ejemplo, el sistema IK vive en un espacio tridimensional, la función de posición puede verse como una función de aplicación . Sea la posición inicial del sistema y ${\displaystyle m}$ ${\displaystyle p(x):\mathbb {R} ^{m}\rightarrow \mathbb {R} ^{3}}$ ${\displaystyle p_{0}=p(x_{0})}$

${\displaystyle p_{1}=p(x_{0}+\Delta x)}$

sea ​​la posición objetivo del sistema. La técnica inversa jacobiana calcula iterativamente una estimación de que minimiza el error dado por . ${\displaystyle \Delta x}$ ${\displaystyle ||p(x_{0}+\Delta x_{estimate})-p_{1}||}$

Para vectores pequeños, la expansión en serie de la función de posición da ${\displaystyle \Delta x}$

${\displaystyle p(x_{1})\approx p(x_{0})+J_{p}(x_{0})\Delta x}$,

donde es la matriz jacobiana (3 × m) de la función de posición en . ${\displaystyle J_{p}(x_{0})}$ ${\displaystyle x_{0}}$

La entrada (i, k)-ésima de la matriz jacobiana se puede aproximar numéricamente

${\displaystyle {\frac {\partial p_{i}}{\partial x_{k}}}\approx {\frac {p_{i}(x_{0,k}+h)-p_{i}(x_{0})}{h}}}$,

donde da el componente i-ésimo de la función de posición, simplemente se agrega un pequeño delta a su componente k-ésimo y es un valor positivo razonablemente pequeño. ${\displaystyle p_{i}(x)}$ ${\displaystyle x_{0,k}+h}$ ${\displaystyle x_{0}}$ ${\displaystyle h}$

Tomando la pseudoinversa de Moore-Penrose del jacobiano (calculable usando una descomposición en valores singulares ) y reordenando los términos se obtiene

${\displaystyle \Delta x\approx J_{p}^{+}(x_{0})\Delta p}$,

dónde . ${\displaystyle \Delta p=p(x_{0}+\Delta x)-p(x_{0})}$

La aplicación del método jacobiano inverso una vez dará como resultado una estimación muy aproximada del vector deseado. Se debe utilizar una búsqueda lineal para escalarlo a un valor aceptable. La estimación de se puede mejorar mediante el siguiente algoritmo (conocido como el método de Newton-Raphson ): ${\displaystyle \Delta x}$ ${\displaystyle \Delta x}$ ${\displaystyle \Delta x}$

${\displaystyle \Delta x_{k+1}=J_{p}^{+}(x_{k})\Delta p_{k}}$

Una vez que algún vector ha hecho que el error caiga cerca de cero, el algoritmo debería terminar. Se ha informado que los métodos existentes basados ​​en la matriz hessiana del sistema convergen a los valores deseados utilizando menos iteraciones, aunque en algunos casos más recursos computacionales. ${\displaystyle \Delta x}$ ${\displaystyle \Delta x}$

Métodos heurísticos

El problema de la cinemática inversa también se puede aproximar utilizando métodos heurísticos. Estos métodos realizan operaciones iterativas simples para conducir gradualmente a una aproximación de la solución. Los algoritmos heurísticos tienen un bajo costo computacional (devuelven la pose final muy rápidamente) y generalmente admiten restricciones conjuntas. Los algoritmos heurísticos más populares son el descenso de coordenadas cíclicas (CCD) ^[11] y la cinemática inversa de alcance hacia adelante y hacia atrás (FABRIK). ^[12]

Véase también

• Portal de física

• 321 estructura cinemática
• Solución de brazo
• Animación cinemática hacia adelante
• Cinemática directa
• Matriz jacobiana y determinante
• Restricciones conjuntas
• Síntesis cinemática
• Cinemación
• Algoritmo de Levenberg-Marquardt
• Captura de movimiento
• Motor de física
• Pseudoinversa
• Física de muñecos de trapo
• Cinemática del robot
• Parámetros de Denavit-Hartenberg

Referencias

1. Donald L. Pieper, La cinemática de los manipuladores bajo control informático. Tesis doctoral, Universidad de Stanford, Departamento de Ingeniería Mecánica, 24 de octubre de 1968.
2. Lynch, Kevin M.; Park, Frank C. (25 de mayo de 2017). Robótica moderna. Cambridge University Press. ISBN 978-1-107-15630-2.
3. Siciliano, Bruno; Khatib, Oussama (27 de junio de 2016). Manual de robótica de Springer. Springer International Publishing. ISBN 978-3-319-32550-7.
4. Paul, Richard (1981). Manipuladores de robots: matemáticas, programación y control: el control informático de los manipuladores de robots. MIT Press, Cambridge, MA. ISBN 978-0-262-16082-7.
5. JM McCarthy, 1990, Introducción a la cinemática teórica, MIT Press, Cambridge, MA.
6. JJ Uicker, GR Pennock y JE Shigley, 2003, Teoría de máquinas y mecanismos, Oxford University Press, Nueva York.
7. JM McCarthy y GS Soh, 2010, Diseño geométrico de vínculos, Springer, Nueva York.
8. Paden, Bradley Evan (1 de enero de 1985). Cinemática y control de manipuladores robóticos (tesis). Código Bibliográfico :1985PhDT........94P.
9. Murray, Richard M.; Li, Zexiang; Sastry, S. Shankar; Sastry, S. Shankara (22 de marzo de 1994). Una introducción matemática a la manipulación robótica. CRC Press. ISBN 978-0-8493-7981-9.
10. A. Aristidou, J. Lasenby, Y. Chrysanthou, A. Shamir. Técnicas de cinemática inversa en gráficos por computadora: una encuesta. Computer Graphics Forum, 37(6): 35-58, 2018.
11. DG Luenberger. 1989. Programación lineal y no lineal. Addison Wesley.
12. A. Aristidou y J. Lasenby. 2011. FABRIK: un solucionador iterativo rápido para el problema de cinemática inversa. Gráfico. Modelos 73, 5, 243–260.

Enlaces externos

• Cinemática inversa de alcance hacia adelante y hacia atrás (FABRIK)
• Robótica y Animación 3D en FreeBasic
• Solucionador de cinemática inversa analítica: dada una descripción cinemática de robot OpenRAVE, genera un archivo C++ que resuelve analíticamente la IK completa.
• Algoritmos de cinemática inversa
• Solución inversa para una geometría de robot común
• Artículo de HowStuffWorks.com ¿Cómo se mueven con tanta fluidez los personajes de los videojuegos? Con una explicación de la cinemática inversa
• Animaciones 3D del cálculo de la cinemática inversa geométrica de un robot industrial
• Teoría cinemática 3D
• Cinemática inversa de proteínas
• Ejemplo simple de cinemática inversa con código fuente utilizando Jacobiano
• Descripción detallada de soluciones jacobianas y CCD para cinemática inversa
• Autodesk HumanIK
• Visualización en 3D de una solución analítica de un robot industrial