El centavo es una unidad de medida logarítmica utilizada para intervalos musicales . El temperamento igual de doce tonos divide la octava en 12 semitonos de 100 cents cada uno. Normalmente, las centésimas se utilizan para expresar intervalos pequeños, para comprobar la entonación o para comparar los tamaños de intervalos comparables en diferentes sistemas de afinación . Para los humanos, un solo céntimo es demasiado pequeño para percibirlo entre notas sucesivas.
Los centavos, tal como los describe Alexander John Ellis , siguen una tradición de medir intervalos mediante logaritmos que comenzó con Juan Caramuel y Lobkowitz en el siglo XVII. [a] Ellis optó por basar sus medidas en la centésima parte de un semitono, 1200 √ 2 , por sugerencia de Robert Holford Macdowell Bosanquet . Al realizar extensas mediciones de instrumentos musicales de todo el mundo, Ellis usó centavos para informar y comparar las escalas empleadas, [1] y describió y utilizó con más detalle el sistema en su edición de 1875 de Sobre las sensaciones del tono de Hermann von Helmholtz . Se ha convertido en el método estándar para representar y comparar tonos e intervalos musicales. [2] [3]
El artículo de Alexander John Ellis Sobre las escalas musicales de varias naciones , [1] publicado por el Journal of the Society of Arts en 1885, introdujo oficialmente el sistema de cents para explorar, comparando y contrastando, escalas musicales de varias naciones. El sistema de cents ya había sido definido en su History of Musical Pitch , donde Ellis escribe: "Si supusiéramos que, entre cada par de notas adyacentes, formando un semitono igual [...], se interpusieran otras 99 notas, haciendo exactamente iguales intervalos entre sí, debemos dividir la octava en 1200 centésimas [ sic ] iguales de un semitono igual, o centésimas , como se les puede llamar brevemente ". [4]
Ellis definió el tono de una nota musical en su obra de 1880 Historia del tono musical [5] como "el número de vibraciones dobles o completas, hacia adelante y hacia atrás, realizadas en cada segundo por una partícula de aire mientras se escucha la nota". [6] Más tarde definió el tono musical como "el tono, o V [para "dobles vibraciones"] de cualquier nota musical nombrada que determina el tono de todas las demás notas en un sistema particular de afinaciones". [7] Señala que estas notas, cuando suenan en sucesión, forman la escala del instrumento, y un intervalo entre dos notas cualesquiera se mide por "la relación entre el número de tono más pequeño y el más grande, o por la fracción formada al dividir el más grande por el más pequeño". [8] Los tonos absolutos y relativos también se definieron en función de estas proporciones. [8]
Ellis señaló que "el objetivo del afinador es hacer que el intervalo [...] entre dos notas cualesquiera que respondan a dos teclas de dedos adyacentes en todo el instrumento sea exactamente el mismo. El resultado se llama temperamento o afinación igual, y es el sistema actualmente se utiliza en toda Europa. [9] Además, ofrece cálculos para aproximar la medida de una proporción en centavos, y agrega que "por regla general, no es necesario ir más allá del número entero más cercano de centavos" .
Ellis presenta aplicaciones del sistema cent en este artículo en escalas musicales de varias naciones, que incluyen: (I. escalas heptatónicas) la antigua Grecia y la Europa moderna, [11] Persia, Arabia, Siria y las Tierras Altas de Escocia, [12] India, [ 13] Singapur, [14] Birmania [15] y Siam; [16] (II. escalas pentatónicas) Pacífico Sur, [17] África Occidental, [18] Java, [19] China [20] y Japón. [21] Y llega a la conclusión de que "la Escala Musical no es una, ni 'natural', ni siquiera fundada necesariamente en las leyes de constitución del sonido musical, tan bellamente elaboradas por Helmholtz, sino muy diversa, muy artificial, y muy caprichosa". [22]
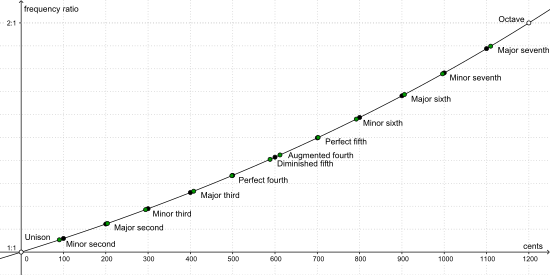
Un centavo es una unidad de medida para la relación entre dos frecuencias. Un semitono igualmente templado (el intervalo entre dos teclas de piano adyacentes) abarca 100 cents por definición. Una octava (dos notas que tienen una relación de frecuencia de 2:1) abarca doce semitonos y, por lo tanto, 1200 cents. La relación de frecuencias separadas por un centavo es exactamente igual a 2 1 ⁄ 1200 = 1200 √ 2 , la raíz 1200 de 2, que es aproximadamente1.000 577 7895 . Así, aumentar una frecuencia en un céntimo corresponde a multiplicar la frecuencia original por este valor constante. Aumentar una frecuencia en 1200 centésimas duplica la frecuencia, lo que da como resultado su octava.
Si se conocen las frecuencias y de dos notas, el número de centésimas que miden el intervalo de a es:
Asimismo, si se conoce y el número de centavos en el intervalo de a , entonces es igual a:
La tercera mayor en entonación justa tiene una relación de frecuencia de 5:4 o ~386 cents, pero en temperamento igual es de 400 cents. Esta diferencia de 14 centavos es aproximadamente una séptima parte de medio paso y es lo suficientemente grande como para ser audible.
A medida que x aumenta de 0 a 1 ⁄ 12 , la función 2 x aumenta casi linealmente desde1.000 00 a1,059 46 , lo que permite una aproximación lineal por partes . Por lo tanto, aunque los centavos representan una escala logarítmica, los intervalos pequeños (menos de 100 centavos) se pueden aproximar vagamente con la relación lineal 1 + 0,000 5946 en lugar de la verdadera relación exponencial 2 c ⁄ 1200 . El error redondeado es cero cuando es 0 o 100, y tiene sólo alrededor de 0,72 centavos de alto en = 50 (cuyo valor correcto de 2 1 ⁄ 24 ≅ 1.029 30 se aproxima por 1 + 0,000 5946 × 50 ≅ 1,02973). Este error está muy por debajo de cualquier cosa humanamente audible, lo que hace que esta aproximación lineal por partes sea adecuada para la mayoría de los propósitos prácticos.
Es difícil establecer cuántos centavos son perceptibles para los humanos; esta precisión varía mucho de persona a persona. Un autor afirmó que los humanos pueden distinguir una diferencia de tono de aproximadamente 5 a 6 centavos. [23] El umbral de lo perceptible, técnicamente conocido como diferencia apenas perceptible (JND), también varía en función de la frecuencia, la amplitud y el timbre . En un estudio, los cambios en la calidad del tono redujeron la capacidad de los estudiantes de música para reconocer, como desafinados, tonos que se desviaban de sus valores apropiados en ±12 centésimas. [24] También se ha establecido que un mayor contexto tonal permite a los oyentes juzgar el tono con mayor precisión. [25] "Si bien los intervalos de menos de unos pocos centavos son imperceptibles para el oído humano en un contexto melódico, en armonía cambios muy pequeños pueden causar grandes cambios en los tiempos y la aspereza de los acordes". [26]
Al escuchar tonos con vibrato , hay evidencia de que los humanos perciben la frecuencia media como el centro del tono. [27] Un estudio de interpretaciones modernas del Ave María de Schubert encontró que la duración del vibrato típicamente oscilaba entre ±34 centavos y ±123 centavos con una media de ±71 centavos y notó una mayor variación en las arias de ópera de Verdi . [28]
Los adultos normales son capaces de reconocer con mucha fiabilidad diferencias de tono de tan sólo 25 cents. Los adultos con amusia , sin embargo, tienen problemas para reconocer diferencias de menos de 100 centavos y, a veces, tienen problemas con estos o intervalos mayores. [29]
La representación de intervalos musicales mediante logaritmos es casi tan antigua como los propios logaritmos. Los logaritmos habían sido inventados por Lord Napier en 1614. [30] Ya en 1647, Juan Caramuel y Lobkowitz (1606-1682) en una carta a Athanasius Kircher describió el uso de logaritmos de base 2 en la música. [31] En esta base, la octava está representada por 1, el semitono por 1/12, etc.
Joseph Sauveur , en sus Principes d'acoustique et de musique de 1701, propuso el uso de logaritmos de base 10, probablemente porque había tablas disponibles. Hizo uso de logaritmos calculados con tres decimales. El logaritmo de base 10 de 2 es igual a aproximadamente 0,301, que Sauveur multiplica por 1000 para obtener 301 unidades en la octava. Para trabajar en unidades más manejables, sugiere tomar 7/301 para obtener unidades de 1/43 de octava. [b] La octava, por tanto, está dividida en 43 partes, llamadas "méridas", divididas a su vez en 7 partes, las "heptaméridas". Sauveur también imaginó la posibilidad de dividir cada heptamérida en 10, pero realmente no utiliza tales unidades microscópicas. [32]
Félix Savart (1791-1841) retomó el sistema de Sauveur, sin limitar el número de decimales del logaritmo de 2, de modo que el valor de su unidad varía según las fuentes. Con cinco decimales, el logaritmo de base 10 de 2 es 0,30103, lo que da 301,03 savarts en la octava. [33] Este valor a menudo se redondea a 1/301 o 1/300 de octava. [34] [35]
A principios del siglo XIX, Gaspard de Prony propuso una unidad logarítmica de base , donde la unidad corresponde a un semitono en temperamento igual. [36] Alexander John Ellis en 1880 describe un gran número de estándares tonales que anotó o calculó, indicando en pronys con dos decimales, es decir con una precisión del 1/100 de semitono, [37] el intervalo que los separaba de un tono teórico de 370 Hz, tomado como punto de referencia. [38]
Un centítono (también Iring ) es un intervalo musical (2 1 ⁄ 600 , ) igual a dos centavos (2 2 ⁄ 1200 ) [39] [40] propuesto como unidad de medida ( ⓘ ) por Widogast Iring en Die reine Stimmung in der Musik (1898) como 600 pasos por octava y más tarde por Joseph Yasser en A Theory of Evolving Tonality (1932) como 100 pasos por tono entero de temperamento igual .
Iring notó que el Grad/Werckmeister (1,96 centavos, 12 por coma pitagórica ) y el cisma (1,95 centavos) son casi iguales (≈ 614 pasos por octava) y ambos pueden aproximarse en 600 pasos por octava (2 centavos). [41] Yasser promovió el decitono , el centitono y el militono (10, 100 y 1000 pasos por tono completo = 60, 600 y 6000 pasos por octava = 20, 2 y 0,2 centavos). [42] [43]
Por ejemplo: Quinta justa de temperamento igual = 700 centavos = 175,6 savarts = 583,3 milioctavas = 350 centítonos. [44]
Los siguientes archivos de audio reproducen varios intervalos. En cada caso, la primera nota que se toca es el do central. La siguiente nota es más aguda que el do según el valor asignado en centésimas. Finalmente, las dos notas se tocan simultáneamente.
Tenga en cuenta que el JND para la diferencia de tono es de 5 a 6 centésimas. Si se tocan por separado, es posible que las notas no muestren una diferencia audible, pero cuando se tocan juntas, se pueden escuchar golpes (por ejemplo, si se tocan el do central y una nota 10 cents más alta). En cualquier instante particular, las dos formas de onda se refuerzan o cancelan entre sí más o menos, dependiendo de su relación de fase instantánea . Un afinador de pianos puede verificar la precisión de la afinación cronometrando los tiempos cuando dos cuerdas suenan a la vez.
ⓘ , frecuencia de batido = 0,16 Hz
ⓘ , frecuencia de batido = 1,53 Hz
ⓘ , frecuencia de batido = 3,81 Hz
![{\displaystyle {\sqrt[{12}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc835f27425fb3140e1f75a5faa35b1e8b9efc35)
![{\displaystyle {\sqrt[{600}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea43c0bc8f62081f2f0b830dd7da893a9d97a9a9)
{{cite book}}: Mantenimiento CS1: falta el editor de la ubicación ( enlace )Las proporciones de intervalo se pueden convertir a los valores de centavos que son de uso común hoy en día.
{{citation}}: Mantenimiento CS1: falta el editor de la ubicación ( enlace )