potencial escalar

Cuando la diferencia de energía potencial depende sólo del desplazamiento.

En física matemática , el potencial escalar , en pocas palabras, describe la situación en la que la diferencia en las energías potenciales de un objeto en dos posiciones diferentes depende sólo de las posiciones, no del camino seguido por el objeto al viajar de una posición a la otra. Es un campo escalar en tres espacios : un valor sin dirección ( escalar ) que depende únicamente de su ubicación. Un ejemplo familiar es la energía potencial debida a la gravedad .

Campo vectorial (derecha) y potencial escalar correspondiente (izquierda).

Un potencial escalar es un concepto fundamental en el análisis vectorial y la física (el adjetivo escalar se omite frecuentemente si no hay peligro de confusión con el potencial vectorial ). El potencial escalar es un ejemplo de campo escalar . Dado un campo vectorial F , el potencial escalar P se define tal que:

${\displaystyle \mathbf {F} =-\nabla P=-\left({\frac {\partial P}{\partial x}},{\frac {\partial P}{\partial y}},{\frac {\partial P}{\partial z}}\right),}$^[1]

donde ∇ P es el gradiente de P y la segunda parte de la ecuación es menos el gradiente para una función de las coordenadas cartesianas x, y, z . ^[a] En algunos casos, los matemáticos pueden usar un signo positivo delante del gradiente para definir el potencial. ^[2] Debido a esta definición de P en términos del gradiente, la dirección de F en cualquier punto es la dirección de la disminución más pronunciada de P en ese punto, su magnitud es la tasa de esa disminución por unidad de longitud.

Para que F se describa únicamente en términos de un potencial escalar, cualquiera de las siguientes afirmaciones equivalentes debe ser verdadera:

1. ${\displaystyle -\int _{a}^{b}\mathbf {F} \cdot d\mathbf {l} =P(\mathbf {b} )-P(\mathbf {a} ),}$donde la integración se realiza sobre un arco de Jordan que pasa de la ubicación a a la ubicación b y P ( b ) se evalúa como P en la ubicación b .
2. ${\displaystyle \oint \mathbf {F} \cdot d\mathbf {l} =0,}$donde la integral es sobre cualquier camino cerrado simple, también conocido como curva de Jordan .
3. ${\displaystyle {\nabla }\times {\mathbf {F} }=0.}$

La primera de estas condiciones representa el teorema fundamental del gradiente y es cierta para cualquier campo vectorial que sea un gradiente de un campo escalar diferenciable de valor único P. La segunda condición es un requisito de F para que pueda expresarse como el gradiente de una función escalar. La tercera condición reexpresa la segunda condición en términos del rizo de F usando el teorema fundamental del rizo . Un campo vectorial F que satisface estas condiciones se dice que es irrotacional (conservador).

Pozo de potencial gravitacional de una masa creciente donde F = –∇ P

Los potenciales escalares desempeñan un papel destacado en muchas áreas de la física y la ingeniería. El potencial de gravedad es el potencial escalar asociado con la gravedad por unidad de masa, es decir, la aceleración debida al campo, en función de la posición. El potencial de gravedad es la energía potencial gravitacional por unidad de masa. En electrostática el potencial eléctrico es el potencial escalar asociado al campo eléctrico , es decir, a la fuerza electrostática por unidad de carga . El potencial eléctrico es en este caso la energía potencial electrostática por unidad de carga. En dinámica de fluidos , los campos laminares irrotacionales tienen un potencial escalar sólo en el caso especial de que se trate de un campo laplaciano . Ciertos aspectos de la fuerza nuclear pueden describirse mediante un potencial de Yukawa . El potencial juega un papel destacado en las formulaciones lagrangianas y hamiltonianas de la mecánica clásica . Además, el potencial escalar es la cantidad fundamental en la mecánica cuántica .

No todos los campos vectoriales tienen un potencial escalar. Las que sí lo hacen se denominan conservadoras , correspondiendo a la noción de fuerza conservativa en física. Ejemplos de fuerzas no conservativas incluyen fuerzas de fricción, fuerzas magnéticas y, en mecánica de fluidos, un campo de velocidad de campo solenoidal . Sin embargo, según el teorema de descomposición de Helmholtz , todos los campos vectoriales pueden describirse en términos de un potencial escalar y su correspondiente potencial vectorial . En electrodinámica, los potenciales escalar y vectorial electromagnético se conocen juntos como cuatro potenciales electromagnéticos .

Condiciones de integrabilidad

Si F es un campo vectorial conservador (también llamado irrotacional , libre de rizos o potencial ), y sus componentes tienen derivadas parciales continuas , el potencial de F con respecto a un punto de referencia r ₀ se define en términos de la integral de línea :

${\displaystyle V(\mathbf {r} )=-\int _{C}\mathbf {F} (\mathbf {r} )\cdot \,d\mathbf {r} =-\int _{a}^{b}\mathbf {F} (\mathbf {r} (t))\cdot \mathbf {r} '(t)\,dt,}$

donde C es una ruta parametrizada desde r ₀ hasta r ,

${\displaystyle \mathbf {r} (t),a\leq t\leq b,\mathbf {r} (a)=\mathbf {r_{0}} ,\mathbf {r} (b)=\mathbf {r} .}$

El hecho de que la integral de línea dependa del camino C sólo a través de sus puntos terminales r ₀ y r es, en esencia, la propiedad de independencia del camino de un campo vectorial conservador. El teorema fundamental de las integrales de línea implica que si V se define de esta manera, entonces F = –∇ V , de modo que V es un potencial escalar del campo vectorial conservador F. El potencial escalar no está determinado únicamente por el campo vectorial: de hecho, el gradiente de una función no se ve afectado si se le agrega una constante. Si V se define en términos de la integral de línea, la ambigüedad de V refleja la libertad en la elección del punto de referencia r ₀ .

Altitud como energía potencial gravitacional.

Campo gravitacional uniforme cerca de la superficie de la Tierra.

Gráfico de una porción bidimensional del potencial gravitacional dentro y alrededor de un cuerpo esférico uniforme. Los puntos de inflexión de la sección transversal están en la superficie del cuerpo.

Un ejemplo es el campo gravitacional (casi) uniforme cerca de la superficie de la Tierra. Tiene una energía potencial.

${\displaystyle U=mgh}$

donde U es la energía potencial gravitacional y h es la altura sobre la superficie. Esto significa que la energía potencial gravitacional en un mapa de contorno es proporcional a la altitud. En un mapa de contornos, el gradiente negativo bidimensional de la altitud es un campo vectorial bidimensional, cuyos vectores son siempre perpendiculares a los contornos y también perpendiculares a la dirección de la gravedad. Pero en la región montañosa representada por el mapa de contorno, el gradiente negativo tridimensional de U siempre apunta directamente hacia abajo en la dirección de la gravedad; F. ​Sin embargo, una bola que rueda cuesta abajo no puede moverse directamente hacia abajo debido a la fuerza normal de la superficie de la colina, que anula la componente de gravedad perpendicular a la superficie de la colina. La componente de la gravedad que queda para mover la pelota es paralela a la superficie:

${\displaystyle \mathbf {F} _{\mathrm {S} }=-mg\ \sin \theta }$

donde θ es el ángulo de inclinación y la componente de F _S perpendicular a la gravedad es

${\displaystyle \mathbf {F} _{\mathrm {P} }=-mg\ \sin \theta \ \cos \theta =-{1 \over 2}mg\sin 2\theta .}$

Esta fuerza F _P , paralela al suelo, es mayor cuando θ tiene 45 grados.

Sea Δ h el intervalo uniforme de altitud entre curvas de nivel en el mapa de curvas de nivel, y sea Δ x la distancia entre dos curvas de nivel. Entonces

$${\displaystyle \theta =\tan ^{-1}{\frac {\Delta h}{\Delta x}}}$$

$${\displaystyle F_{P}=-mg{\Delta x\,\Delta h \over \Delta x^{2}+\Delta h^{2}}.}$$

Δ xF _P

Presión como potencial de flotación

En mecánica de fluidos , un fluido en equilibrio, pero en presencia de un campo gravitacional uniforme, está permeado por una fuerza de flotación uniforme que anula la fuerza gravitacional: así es como el fluido mantiene su equilibrio. Esta fuerza de flotación es el gradiente negativo de presión :

${\displaystyle \mathbf {f_{B}} =-\nabla p.\,}$

Dado que la fuerza de flotación apunta hacia arriba, en dirección opuesta a la gravedad, la presión en el fluido aumenta hacia abajo. La presión en un cuerpo de agua estático aumenta proporcionalmente a la profundidad debajo de la superficie del agua. Las superficies de presión constante son planos paralelos a la superficie, que se puede caracterizar como el plano de presión cero.

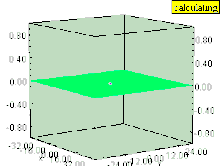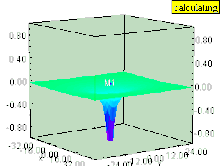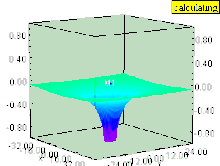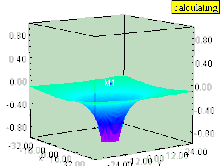
Si el líquido tiene un vórtice vertical (cuyo eje de rotación es perpendicular a la superficie), entonces el vórtice provoca una depresión en el campo de presión. La superficie del líquido dentro del vórtice es arrastrada hacia abajo, al igual que cualquier superficie de igual presión, que aún permanece paralela a la superficie del líquido. El efecto es más fuerte dentro del vórtice y disminuye rápidamente con la distancia desde el eje del vórtice.

La fuerza de flotación debida a un fluido sobre un objeto sólido sumergido y rodeado por ese fluido se puede obtener integrando el gradiente de presión negativa a lo largo de la superficie del objeto:

${\displaystyle F_{B}=-\oint _{S}\nabla p\cdot \,d\mathbf {S} .}$

Potencial escalar en el espacio euclidiano

En el espacio euclidiano tridimensional , el potencial escalar de un campo vectorial irrotacional E viene dado por ${\displaystyle \mathbb {R} ^{3}}$

$${\displaystyle \Phi (\mathbf {r} )={1 \over 4\pi }\int _{\mathbb {R} ^{3}}{\frac {\operatorname {div} \mathbf {E} (\mathbf {r} ')}{\|\mathbf {r} -\mathbf {r} '\|}}\,dV(\mathbf {r} ')}$$

dV ( r' )r'

$${\displaystyle \mathbf {E} =-\mathbf {\nabla } \Phi =-{1 \over 4\pi }\mathbf {\nabla } \int _{\mathbb {R} ^{3}}{\frac {\operatorname {div} \mathbf {E} (\mathbf {r} ')}{\|\mathbf {r} -\mathbf {r} '\|}}\,dV(\mathbf {r} ')}$$

Econtinua1/ rdivergenciaE1/ r ²

Escrito de otra manera, vamos

$${\displaystyle \Gamma (\mathbf {r} )={\frac {1}{4\pi }}{\frac {1}{\|\mathbf {r} \|}}}$$

potencial newtonianosolución fundamentalecuación de LaplaceΓfunción delta de Dirac

${\displaystyle \nabla ^{2}\Gamma (\mathbf {r} )+\delta (\mathbf {r} )=0.}$

Entonces el potencial escalar es la divergencia de la convolución de E con Γ :

${\displaystyle \Phi =\operatorname {div} (\mathbf {E} *\Gamma ).}$

De hecho, la convolución de un campo vectorial irrotacional con un potencial rotacionalmente invariante también es irrotacional. Para un campo vectorial irrotacional G , se puede demostrar que

$${\displaystyle \nabla ^{2}\mathbf {G} =\mathbf {\nabla } (\mathbf {\nabla } \cdot {}\mathbf {G} ).}$$

$${\displaystyle \nabla \operatorname {div} (\mathbf {E} *\Gamma )=\nabla ^{2}(\mathbf {E} *\Gamma )=\mathbf {E} *\nabla ^{2}\Gamma =-\mathbf {E} *\delta =-\mathbf {E} }$$

De manera más general, la fórmula

$${\displaystyle \Phi =\operatorname {div} (\mathbf {E} *\Gamma )}$$

nn > 2

$${\displaystyle \Gamma (\mathbf {r} )={\frac {1}{n(n-2)\omega _{n}\|\mathbf {r} \|^{n-2}}}}$$

ω _nnpropiedades de convolución

$${\displaystyle \Phi (\mathbf {r} )=-{\frac {1}{n\omega _{n}}}\int _{\mathbb {R} ^{n}}{\frac {\mathbf {E} (\mathbf {r} ')\cdot (\mathbf {r} -\mathbf {r} ')}{\|\mathbf {r} -\mathbf {r} '\|^{n}}}\,dV(\mathbf {r} ').}$$

Ver también

• Teorema del gradiente
• Teorema fundamental del análisis vectorial.
• Líneas y superficies equipotenciales (isopotenciales)

Notas

1. La segunda parte de esta ecuación solo es válida para coordenadas cartesianas, otros sistemas de coordenadas como las coordenadas cilíndricas o esféricas tendrán representaciones más complicadas, derivadas del teorema fundamental del gradiente .

Referencias

1. Herbert Goldstein. Mecánica clásica (2 ed.). págs. 3–4. ISBN 978-0-201-02918-5.
2. Consulte [1] para ver un ejemplo en el que el potencial se define sin negativo. Otras referencias como Louis Leithold, The Calculus with Analytic Geometry (5 ed.), p. 1199Evite utilizar el término potencial al resolver una función a partir de su gradiente.

enlaces externos

• Medios relacionados con el potencial escalar en Wikimedia Commons