
La aritmética elemental es una rama de las matemáticas que incluye la suma , la resta , la multiplicación y la división . Debido a su bajo nivel de abstracción , su amplia gama de aplicaciones y su posición como base de todas las matemáticas, la aritmética elemental es generalmente la primera rama de las matemáticas que se enseña en las escuelas. [1] [2]
En los sistemas de numeración , los dígitos son caracteres que se utilizan para representar el valor de los números. Un ejemplo de un sistema de numeración es el sistema de numeración indoárabe predominantemente utilizado (0 a 9), que utiliza una notación posicional decimal . [3] Otros sistemas de numeración incluyen el sistema Kaktovik (a menudo utilizado en las lenguas esquimal-aleutianas de Alaska , Canadá y Groenlandia ), y es un sistema de notación posicional vigesimal . [4] Independientemente del sistema de numeración utilizado, los resultados de las operaciones aritméticas no se ven afectados.
En aritmética elemental, el sucesor de un número natural (incluido el cero) es el siguiente número natural y es el resultado de sumarle uno. El predecesor de un número natural (excluido el cero) es el número natural anterior y es el resultado de restarle uno. Por ejemplo, el sucesor del cero es uno y el predecesor del once es diez ( y ). Todo número natural tiene un sucesor y todo número natural excepto el 0 tiene un predecesor. [5]
Los números naturales tienen un orden total . Si un número es mayor que ( ) otro número, entonces este último es menor que ( ) el primero. Por ejemplo, tres es menor que ocho ( ), por lo tanto, ocho es mayor que tres ( ). Los números naturales también están bien ordenados , lo que significa que cualquier subconjunto de los números naturales tiene un elemento menor .
El conteo asigna un número natural a cada objeto de un conjunto , comenzando con 1 para el primer objeto y aumentando en 1 para cada objeto subsiguiente. La cantidad de objetos en el conjunto es el recuento. Esto también se conoce como la cardinalidad del conjunto.
Contar también puede ser el proceso de hacer un recuento , el proceso de dibujar una marca para cada objeto de un conjunto.
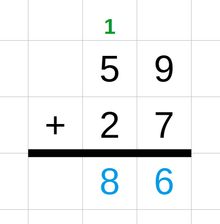
La suma es una operación matemática que combina dos o más números (llamados sumandos) para producir un número combinado (llamado suma). La suma de dos números se expresa con el signo más ( ). [6] Se realiza de acuerdo con estas reglas:
Cuando la suma de un par de dígitos da como resultado un número de dos dígitos, el dígito de las "decenas" se denomina "dígito de acarreo". [9] En aritmética elemental, los estudiantes generalmente aprenden a sumar números enteros y también pueden aprender sobre temas como números negativos y fracciones .
La resta evalúa la diferencia entre dos números, donde el minuendo es el número que se resta y el sustraendo es el número que se resta. Se representa mediante el signo menos ( ). El signo menos también se utiliza para indicar números negativos.
La resta no es conmutativa, lo que significa que el orden de los números puede cambiar el valor final; no es lo mismo que . En aritmética elemental, el minuendo siempre es mayor que el sustraendo para producir un resultado positivo.
La resta también se utiliza para separar, combinar (por ejemplo, encontrar el tamaño de un subconjunto de un conjunto específico) y encontrar cantidades en otros contextos.
Existen varios métodos para realizar restas. El método matemático tradicional resta utilizando métodos adecuados para el cálculo manual. [10] Las matemáticas reformistas se distinguen, en general, por la falta de preferencia por una técnica específica, en su lugar se guía a los estudiantes para que inventen sus propios métodos de cálculo.
Las escuelas estadounidenses enseñan un método de resta que utiliza préstamos. [11] Un problema de resta como el que se resuelve tomando prestado un 10 del lugar de las decenas para sumarlo al lugar de las unidades con el fin de facilitar la resta. Restar 9 de 6 implica tomar prestado un 10 del lugar de las decenas, convirtiendo el problema en . Esto se indica tachando el 8, escribiendo un 7 encima y escribiendo un 1 encima del 6. Estas marcas se llaman "muletas", que fueron inventadas por William A. Brownell , quien las utilizó en un estudio, en noviembre de 1937. [12]
El método austriaco, también conocido como método de adición, se enseña en ciertos países europeos [¿ cuáles? ] . A diferencia del método anterior, no se utilizan préstamos, aunque hay muletas que varían según ciertos países. [13] [14] El método de adición implica aumentar el sustraendo. Esto transforma el problema anterior en . Se marca un pequeño 1 debajo del dígito del sustraendo como recordatorio.
Restando los números 792 y 308, comenzando con la columna de las unidades, 2 es menor que 8. Usando el método de préstamo, se toma prestado 10 de 90, reduciendo 90 a 80. Esto cambia el problema a .
En la columna de las decenas, la diferencia entre 80 y 0 es 80.
En la columna de las centenas, la diferencia entre 700 y 300 es 400.
El resultado:
La multiplicación es una operación matemática de adición repetida. Cuando se multiplican dos números, el valor resultante es un producto. Los números que se multiplican son multiplicandos, multiplicadores o factores. La multiplicación se puede expresar como "cinco por tres es igual a quince", "cinco por tres es quince" o "quince es el producto de cinco por tres".
La multiplicación se representa mediante el signo de multiplicación (×), el asterisco (*), los paréntesis () o el punto (⋅). La expresión "cinco por tres es igual a quince" se puede escribir como " ", " ", " " o " ".
En aritmética elemental, la multiplicación satisface las siguientes propiedades [a] :
En el algoritmo de multiplicación, el dígito de las "decenas" del producto de un par de dígitos se denomina "dígito de acarreo".
Al multiplicar 729 y 3, comenzando en la columna de las unidades, el producto de 9 y 3 es 27. 7 se escribe debajo de la columna de las unidades y 2 se escribe encima de la columna de las decenas como dígito de acarreo.
El producto de 2 y 3 es 6, y el dígito de acarreo suma 2 a 6, por lo que 8 se escribe debajo de la columna de las decenas.
El producto de 7 y 3 es 21, y como este es el último dígito, 2 no se escribirá como dígito de acarreo, sino al lado de 1.
El resultado:
Multiplicando 789 y 345, empezando por la columna de las unidades, el producto de 789 y 5 es 3945.
El 4 está en el dígito de las decenas. El multiplicador es 40, no 4. El producto de 789 y 40 es 31560.
El 3 está en el dígito de las centenas. El multiplicador es 300. El producto de 789 y 300 es 236700.
Añadiendo todos los productos,
El resultado:
La división es una operación aritmética y la inversa de la multiplicación . Dado que , ,
La división se puede escribir como , , o a ⁄ b . Esto se puede leer verbalmente como " a dividido por b " o " a sobre b ".
En algunas culturas que no hablan inglés [ ¿cuáles? ] , " a dividido por b " se escribe a : b . En el uso del inglés, los dos puntos se limitan al concepto de proporciones (" a es a b ").
En una ecuación , a es el dividendo, b el divisor y c el cociente. La división por cero se considera imposible a nivel aritmético elemental.
Dos números se pueden dividir en papel mediante la división larga . Se puede utilizar una versión abreviada de la división larga, la división corta , para divisores más pequeños.
Un método menos sistemático implica el concepto de fragmentación , que implica restar más múltiplos del resto parcial en cada etapa.
Dividiendo 272 y 8, comenzando con el dígito de las centenas, 2 no es divisible por 8. Suma 20 y 7 para obtener 27. El número más grande por el que se puede multiplicar el divisor de 8 sin exceder 27 es 3, por lo que se escribe debajo de la columna de las decenas. Restar 24 (el producto de 3 y 8) de 27 da 3 como resto .
Pasando a la cifra de las unidades, el número es 2. Sumando 30 (el resto, 3, por 10) y 2 se obtiene 32. El cociente de 32 y 8 es 4, que está escrito debajo de la columna de las unidades.
El resultado:
Otro método de división que se enseña en algunas escuelas es el método de la parada de autobús, a veces denominado
resultado (divisor) dividend
Los pasos a seguir se muestran a continuación, utilizando el mismo ejemplo que el anterior:
0 3 4 8|272 0 (8 × 0 = 0) 2 7 ( 2 - 0 = 2 ) 24 ( 8 × 3 = 24) 3 2 (27 - 24 = 3 ) 32 ( 8 × 4 = 32) 0 (32 - 32 = 0)
El resultado:
La aritmética elemental se enseña generalmente en los niveles de primaria o secundaria y se rige por los estándares educativos locales. En los Estados Unidos y Canadá, ha habido debate sobre el contenido y los métodos utilizados para enseñar aritmética elemental. [15] [16]