stringtranslate.com

Análisis de decisiones con criterios múltiples

Gráfico de dos criterios para maximizar el rendimiento y minimizar el riesgo en carteras financieras (puntos óptimos de Pareto en puntos rojos)

La toma de decisiones con criterios múltiples ( MCDM ) o el análisis de decisiones con criterios múltiples ( MCDA ) es una subdisciplina de la investigación operativa que evalúa explícitamente múltiples criterios conflictivos en la toma de decisiones (tanto en la vida diaria como en entornos como los negocios, el gobierno y la medicina). ). Los criterios contradictorios son típicos al evaluar opciones: el costo o el precio suele ser uno de los criterios principales, y alguna medida de calidad suele ser otro criterio, que fácilmente entra en conflicto con el costo. Al comprar un automóvil, el costo, la comodidad, la seguridad y el ahorro de combustible pueden ser algunos de los principales criterios que consideramos: no es habitual que el automóvil más barato sea el más cómodo y seguro. En la gestión de carteras , los gestores están interesados ​​en obtener altos rendimientos y al mismo tiempo reducir los riesgos; sin embargo, las acciones que tienen el potencial de generar altos rendimientos suelen conllevar un alto riesgo de perder dinero. En una industria de servicios, la satisfacción del cliente y el costo de brindar el servicio son criterios fundamentales en conflicto.

En su vida diaria, las personas suelen sopesar implícitamente múltiples criterios y pueden sentirse cómodas con las consecuencias de decisiones que se toman basándose únicamente en la intuición . [1] Por otro lado, cuando hay mucho en juego, es importante estructurar adecuadamente el problema y evaluar explícitamente múltiples criterios. [2] Al tomar la decisión de construir o no una planta de energía nuclear, y dónde construirla, no sólo hay cuestiones muy complejas que involucran múltiples criterios, sino que también hay múltiples partes que se ven profundamente afectadas por las consecuencias.

Estructurar bien problemas complejos y considerar múltiples criterios explícitamente conduce a decisiones mejores y más informadas. Ha habido avances importantes en este campo desde el inicio de la disciplina moderna de toma de decisiones con criterios múltiples a principios de los años sesenta. Se han desarrollado una variedad de enfoques y métodos, muchos implementados mediante software especializado para la toma de decisiones , [3] [4] para su aplicación en una variedad de disciplinas, que van desde la política y los negocios hasta el medio ambiente y la energía. [5]

Fundamentos, conceptos, definiciones.

MCDM o MCDA son siglas de toma de decisiones con múltiples criterios y análisis de decisiones con múltiples criterios . Stanley Zionts ayudó a popularizar el acrónimo con su artículo de 1979 "MCDM - Si no es un número romano, ¿entonces qué?", ​​dirigido a un público empresarial.

MCDM se ocupa de estructurar y resolver problemas de decisión y planificación que involucran múltiples criterios. El propósito es apoyar a los tomadores de decisiones que enfrentan tales problemas. Normalmente, no existe una solución óptima única para tales problemas y es necesario utilizar las preferencias de quienes toman las decisiones para diferenciar entre soluciones.

"Resolver" se puede interpretar de diferentes maneras. Podría corresponder a elegir la "mejor" alternativa entre un conjunto de alternativas disponibles (donde "mejor" puede interpretarse como "la alternativa preferida" por quien toma las decisiones). Otra interpretación de "resolver" podría ser elegir un pequeño conjunto de buenas alternativas o agrupar alternativas en diferentes conjuntos de preferencias. Una interpretación extrema podría ser encontrar todas las alternativas "eficientes" o " no dominadas " (que definiremos en breve).

La dificultad del problema proviene de la presencia de más de un criterio. Ya no existe una solución óptima única para un problema MCDM que pueda obtenerse sin incorporar información de preferencias. El concepto de solución óptima a menudo es reemplazado por el conjunto de soluciones no dominadas. Una solución se llama no dominada si no es posible mejorarla en ningún criterio sin sacrificarla en otro. Por lo tanto, tiene sentido que quien toma las decisiones elija una solución del conjunto no dominado. De lo contrario, podría obtener mejores resultados en algunos o todos los criterios y no peor en ninguno de ellos. Sin embargo, en general, el conjunto de soluciones no dominadas es demasiado grande para presentárselo a quien toma las decisiones para la elección final. Por lo tanto, necesitamos herramientas que ayuden a quien toma las decisiones a centrarse en las soluciones (o alternativas) preferidas. Normalmente uno tiene que "compensar" ciertos criterios por otros.

MCDM ha sido un área activa de investigación desde la década de 1970. Hay varias organizaciones relacionadas con MCDM, incluida la Sociedad Internacional para la Toma de Decisiones Multicriterio, [6] el Grupo de Trabajo Euro sobre MCDA, [7] y la Sección INFORMS sobre MCDM. [8] Para una historia ver: Köksalan, Wallenius y Zionts (2011). [9] MCDM se basa en conocimientos de muchos campos, entre ellos:

una tipología

Existen diferentes clasificaciones de problemas y métodos de MCDM. Una distinción importante entre los problemas MCDM se basa en si las soluciones están definidas explícita o implícitamente.

Ya sea que se trate de un problema de evaluación o de diseño, se requiere información de preferencias de los DM para diferenciar entre soluciones. Los métodos de solución para problemas MCDM se clasifican comúnmente según el momento de la información de preferencia obtenida del DM.

Hay métodos que requieren la información de preferencia del DM al inicio del proceso, transformando el problema esencialmente en un problema de criterio único. Se dice que estos métodos funcionan mediante "articulación previa de preferencias". Los métodos basados ​​en la estimación de una función de valor o el uso del concepto de "relaciones superiores", el proceso de jerarquía analítica y algunos métodos de decisión basados ​​en reglas intentan resolver problemas de evaluación de múltiples criterios utilizando la articulación previa de preferencias. De manera similar, existen métodos desarrollados para resolver problemas de diseño de criterios múltiples utilizando la articulación previa de preferencias mediante la construcción de una función de valor. Quizás el más conocido de estos métodos sea la programación por objetivos. Una vez construida la función de valor, el programa matemático de objetivo único resultante se resuelve para obtener una solución preferida.

Algunos métodos requieren información de preferencias del DM durante todo el proceso de solución. Estos se denominan métodos interactivos o métodos que requieren una "articulación progresiva de preferencias". Estos métodos han sido bien desarrollados tanto para la evaluación de criterios múltiples (ver, por ejemplo, Geoffrion, Dyer y Feinberg, 1972, [11] y Köksalan y Sagala, 1995 [12] ) como para problemas de diseño (ver Steuer, 1986 [13] ).

Los problemas de diseño de criterios múltiples generalmente requieren la solución de una serie de modelos de programación matemática para revelar soluciones definidas implícitamente. Para estos problemas, también puede resultar interesante una representación o aproximación de "soluciones eficientes". Esta categoría se conoce como "articulación posterior de preferencias", lo que implica que la participación del DM comienza posterior a la revelación explícita de soluciones "interesantes" (ver, por ejemplo, Karasakal y Köksalan, 2009 [ 14] ).

Cuando los modelos de programación matemática contienen variables enteras, los problemas de diseño se vuelven más difíciles de resolver. La optimización combinatoria multiobjetivo (MOCO) constituye una categoría especial de este tipo de problemas que plantean una dificultad computacional sustancial (ver Ehrgott y Gandibleux, [15] 2002, para una revisión).

Representaciones y definiciones

El problema MCDM se puede representar en el espacio de criterios o en el espacio de decisión. Alternativamente, si se combinan diferentes criterios mediante una función lineal ponderada, también es posible representar el problema en el espacio de ponderación. A continuación se muestran las demostraciones de los espacios de criterio y peso, así como algunas definiciones formales.

Representación del espacio de criterios

Supongamos que evaluamos soluciones en una situación problemática específica utilizando varios criterios. Supongamos además que más es mejor en cada criterio. Entonces, entre todas las soluciones posibles, lo ideal es que nos interesen aquellas que funcionan bien en todos los criterios considerados. Sin embargo, es poco probable que exista una única solución que funcione bien en todos los criterios considerados. Normalmente, algunas soluciones funcionan bien en algunos criterios y otras funcionan bien en otros. Encontrar una manera de equilibrar los criterios es uno de los principales esfuerzos en la literatura sobre MCDM.

Matemáticamente, el problema MCDM correspondiente a los argumentos anteriores se puede representar como

"máximo" q
sujeto a
q ∈ Q

donde q es el vector de k funciones criterio (funciones objetivo) y Q es el conjunto factible, Q ⊆ R k .

Si Q se define explícitamente (mediante un conjunto de alternativas), el problema resultante se denomina problema de evaluación de criterios múltiples.

Si Q se define implícitamente (mediante un conjunto de restricciones), el problema resultante se denomina problema de diseño de criterios múltiples.

Las comillas se utilizan para indicar que la maximización de un vector no es una operación matemática bien definida. Esto corresponde al argumento de que tendremos que encontrar una manera de resolver el equilibrio entre criterios (generalmente basado en las preferencias de quien toma las decisiones) cuando no existe una solución que funcione bien en todos los criterios.

Representación del espacio de decisión

El espacio de decisión corresponde al conjunto de posibles decisiones que tenemos a nuestra disposición. Los valores de los criterios serán consecuencias de las decisiones que tomemos. Por tanto, podemos definir un problema correspondiente en el espacio de decisión. Por ejemplo, al diseñar un producto, decidimos los parámetros de diseño (variables de decisión), cada uno de los cuales afecta las medidas de desempeño (criterios) con las que evaluamos nuestro producto.

Matemáticamente, un problema de diseño de criterios múltiples se puede representar en el espacio de decisión de la siguiente manera:

donde X es el conjunto factible y x es el vector de variable de decisión de tamaño n.

Se obtiene un caso especial bien desarrollado cuando X es un poliedro definido por desigualdades e igualdades lineales. Si todas las funciones objetivo son lineales en términos de las variables de decisión, esta variación conduce a la programación lineal objetiva múltiple (MOLP), una subclase importante de los problemas MCDM.

Hay varias definiciones que son centrales en MCDM. Dos definiciones estrechamente relacionadas son las de no dominancia (definida en función de la representación del espacio de criterios) y eficiencia (definida en función de la representación de la variable de decisión).

Definición 1. q* ∈ Q es no dominado si no existe otro q ∈ Q tal que q ≥ q* y q ≠ q* .

En términos generales, una solución no está dominada siempre que no sea inferior a cualquier otra solución disponible en todos los criterios considerados.

Definición 2. x* ∈ X es eficiente si no existe otro x ∈ X tal que f ( x ) ≥ f ( x *) y f ( x ) ≠ f ( x *) .

Si un problema MCDM representa bien una situación de decisión, entonces la solución preferida de un DM tiene que ser una solución eficiente en el espacio de decisión, y su imagen es un punto no dominado en el espacio de criterios. Las siguientes definiciones también son importantes.

Definición 3. q* ∈ Q es débilmente no dominado si no existe otro q ∈ Q tal que q > q* .

Definición 4. x* ∈ X es débilmente eficiente si no existe otro x ∈ X tal que f ( x ) > f ( x *) .

Los puntos débilmente no dominados incluyen todos los puntos no dominados y algunos puntos dominados especiales. La importancia de estos puntos dominados especiales proviene del hecho de que aparecen comúnmente en la práctica y es necesario tener especial cuidado para distinguirlos de los puntos no dominados. Si, por ejemplo, maximizamos un único objetivo, podemos terminar con un punto débilmente no dominado que sí está dominado. Los puntos dominados del conjunto débilmente no dominado se ubican en planos verticales u horizontales (hiperplanos) en el espacio de criterios.

Punto ideal : (en el espacio de criterios) representa lo mejor (el máximo para problemas de maximización y el mínimo para problemas de minimización) de cada función objetivo y normalmente corresponde a una solución inviable.

Punto nadir : (en el espacio de criterios) representa lo peor (el mínimo para problemas de maximización y el máximo para problemas de minimización) de cada función objetivo entre los puntos del conjunto no dominado y normalmente es un punto dominado.

El punto ideal y el punto nadir son útiles para que el DM tenga una "sensación" de la gama de soluciones (aunque no es sencillo encontrar el punto nadir para problemas de diseño que tienen más de dos criterios).

Ilustraciones de los espacios de decisión y criterio.

El siguiente problema MOLP de dos variables en el espacio de variables de decisión ayudará a demostrar gráficamente algunos de los conceptos clave.

Figura 1. Demostración del espacio de decisión

En la Figura 1, los puntos extremos "e" y "b" maximizan el primer y segundo objetivo, respectivamente. El límite rojo entre esos dos puntos extremos representa el conjunto eficiente. Se puede ver en la figura que, para cualquier solución factible fuera del conjunto eficiente, es posible mejorar ambos objetivos en algunos puntos del conjunto eficiente. Por el contrario, para cualquier punto del conjunto eficiente, no es posible mejorar ambos objetivos pasando a cualquier otra solución factible. En estas soluciones, uno tiene que sacrificar uno de los objetivos para mejorar el otro objetivo.

Debido a su simplicidad, el problema anterior se puede representar en el espacio de criterios reemplazando las x con las f de la siguiente manera:

Figura 2. Demostración de las soluciones en el espacio de criterios.
f máx 1
f máx 2
sujeto a
f 1 + 2 f 2 ≤ 12
2 f 1 + f 2 ≤ 12
f 1 + f 2 ≤ 7
f 1 – f 2 ≤ 9
− f 1 + f 2 ≤ 9
f 1 + 2 f 2 ≥ 0
2 f 1 + f 2 ≥ 0

Presentamos el espacio de criterios gráficamente en la Figura 2. Es más fácil detectar los puntos no dominados (correspondientes a soluciones eficientes en el espacio de decisión) en el espacio de criterios. La región noreste del espacio factible constituye el conjunto de puntos no dominados (para problemas de maximización).

Generando soluciones no dominadas

Hay varias formas de generar soluciones no dominadas. Discutiremos dos de estos. El primer enfoque puede generar una clase especial de soluciones no dominadas, mientras que el segundo enfoque puede generar cualquier solución no dominada.

Si combinamos los múltiples criterios en un solo criterio multiplicando cada criterio con un peso positivo y sumando los criterios ponderados, entonces la solución al problema de criterio único resultante es una solución eficiente especial. Estas soluciones especiales eficientes aparecen en los puntos angulares del conjunto de soluciones disponibles. Las soluciones eficientes que no se encuentran en puntos de esquina tienen características especiales y este método no es capaz de encontrar dichos puntos. Matemáticamente, podemos representar esta situación como

máx w T . q = w T . f(x) , w > 0
sujeto a
x∈X _ _

Al variar los pesos, se pueden utilizar sumas ponderadas para generar soluciones de puntos extremos eficientes para problemas de diseño y puntos apoyados (convexos no dominados) para problemas de evaluación.

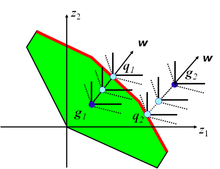
Figura 3. Proyectar puntos sobre el conjunto no dominado con una función de escalarización de logros

Las funciones de escalarización de logros también combinan múltiples criterios en un solo criterio ponderándolos de una manera muy especial. Crean contornos rectangulares que se alejan de un punto de referencia hacia las soluciones eficientes disponibles. Esta estructura especial potencia las funciones de escalarización de logros para alcanzar cualquier solución eficiente. Esta es una propiedad poderosa que hace que estas funciones sean muy útiles para problemas de MCDM.

Matemáticamente, podemos representar el problema correspondiente como

Min s ( g, q, w, ρ ) = Min {max i [( g i − q i )/ w i ] + ρ Σ i ( g i − q i ) },
sujeto a
q ∈ Q

La función de escalarización de logros se puede utilizar para proyectar cualquier punto (factible o no factible) en la frontera eficiente. Se puede alcanzar cualquier punto (soportado o no). El segundo término de la función objetivo es necesario para evitar generar soluciones ineficientes. La Figura 3 demuestra cómo un punto factible, g 1 , y un punto no factible, g 2 , se proyectan sobre los puntos no dominados, q 1 y q 2 , respectivamente, a lo largo de la dirección w utilizando una función de escalarización de logros. Los contornos discontinuos y sólidos corresponden a los contornos de la función objetivo con y sin el segundo término de la función objetivo, respectivamente.

Resolviendo problemas de MCDM

Se han desarrollado diferentes escuelas de pensamiento para la resolución de problemas MCDM (tanto del tipo diseño como de evaluación). Para un estudio bibliométrico que muestra su evolución a lo largo del tiempo, véase Bragge, Korhonen, H. Wallenius y J. Wallenius [2010]. [18]

Escuela de programación matemática de objetivos múltiples.

(1) Maximización de vectores : El propósito de la maximización de vectores es aproximar el conjunto no dominado; desarrollado originalmente para problemas de programación lineal objetiva múltiple (Evans y Steuer, 1973; [19] Yu y Zeleny, 1975 [20] ).

(2) Programación interactiva : las fases de computación se alternan con fases de toma de decisiones (Benayoun et al., 1971; [21] Geoffrion, Dyer y Feinberg, 1972; [22] Zionts y Wallenius, 1976; [23] Korhonen y Wallenius , 1988 [24] ). No se supone ningún conocimiento explícito de la función de valor del DM.

escuela de programación de objetivos

El propósito es establecer valores objetivo a priori para las metas y minimizar las desviaciones ponderadas de estas metas. Se han utilizado tanto ponderaciones de importancia como ponderaciones lexicográficas preventivas (Charnes y Cooper, 1961 [25] ).

Teóricos del conjunto difuso

Zadeh (1965) [26] introdujo los conjuntos difusos como una extensión de la noción clásica de conjuntos. Esta idea se utiliza en muchos algoritmos MCDM para modelar y resolver problemas difusos.

Métodos basados ​​en datos ordinales

Los datos ordinales tienen una amplia aplicación en situaciones del mundo real. En este sentido, algunos métodos MCDM fueron diseñados para manejar datos ordinales como datos de entrada. Por ejemplo, el método de prioridad ordinal y el método Qualiflex.

Teóricos de la utilidad de atributos múltiples

Se obtienen y utilizan funciones de valor o utilidad de atributos múltiples para identificar la alternativa más preferida o para clasificar las alternativas. Se pueden utilizar técnicas de entrevista elaboradas, que existen para obtener funciones de utilidad aditivas lineales y funciones de utilidad no lineales multiplicativas (Keeney y Raiffa, 1976 [27] ). Otro enfoque consiste en obtener funciones de valor indirectamente planteando a quien toma las decisiones una serie de preguntas de clasificación por pares que implican elegir entre alternativas hipotéticas ( método PAPRIKA ; Hansen y Ombler, 2008 [28] ).

escuela francesa

La escuela francesa se centra en la ayuda a la toma de decisiones, en particular la familia ELECTRE de métodos de clasificación superior que se originó en Francia a mediados de la década de 1960. El método fue propuesto por primera vez por Bernard Roy (Roy, 1968 [29] ).

Escuela evolutiva de optimización multiobjetivo (EMO)

Los algoritmos EMO comienzan con una población inicial y la actualizan mediante el uso de procesos diseñados para imitar los principios naturales de supervivencia del más apto y los operadores de variación genética para mejorar la población promedio de una generación a la siguiente. El objetivo es converger a una población de soluciones que representen el conjunto no dominado (Schaffer, 1984; [30] Srinivas y Deb, 1994 [31] ). Más recientemente, hay esfuerzos para incorporar información de preferencias en el proceso de solución de algoritmos EMO (ver Deb y Köksalan, 2010 [32] ).

Métodos basados ​​en la teoría del sistema gris.

En la década de 1980, Deng Julong propuso la teoría del sistema Gray (GST) y su primer modelo de toma de decisiones de atributos múltiples, llamado modelo de análisis relacional Gray (GRA) de Deng. Más tarde, los estudiosos de los sistemas grises propusieron muchos métodos basados ​​en GST, como el modelo GRA absoluto de Liu Sifeng , [33] la toma de decisiones con objetivos grises (GTDM) [34] y el análisis de decisiones absolutas grises (GADA). [35]

Proceso de jerarquía analítica (AHP)

El AHP primero descompone el problema de decisión en una jerarquía de subproblemas. Luego, quien toma las decisiones evalúa la importancia relativa de sus diversos elementos mediante comparaciones por pares. El AHP convierte estas evaluaciones en valores numéricos (ponderaciones o prioridades), que se utilizan para calcular una puntuación para cada alternativa (Saaty, 1980 [36] ). Un índice de consistencia mide el grado en que quien toma las decisiones ha sido consistente en sus respuestas. AHP es una de las técnicas más controvertidas enumeradas aquí, y algunos investigadores de la comunidad MCDA creen que es defectuosa. [37] [38] Las matemáticas subyacentes también son más complicadas y requieren un análisis racional [ vago ] , [38] aunque han ganado cierta popularidad como resultado del software disponible comercialmente.

Varios artículos revisaron la aplicación de técnicas MCDM en diversas disciplinas como MCDM difuso, [39] MCDM clásico, [40] energía sostenible y renovable, [41] técnica VIKOR, [42] sistemas de transporte, [43] calidad del servicio, [44 ] método TOPSIS, [45] problemas de gestión energética, [46] e-learning, [47] turismo y hostelería, [48] métodos SWARA y WASPAS. [49]

Métodos MCDM

Están disponibles los siguientes métodos MCDM, muchos de los cuales se implementan mediante software especializado en la toma de decisiones : [3] [4]

Ver también

Referencias

  1. ^ Rew, L. (1988). "Intuición en la toma de decisiones". Revista de Becas de Enfermería . 20 (3): 150-154. doi :10.1111/j.1547-5069.1988.tb00056.x. PMID  3169833.
  2. ^ Franco, Los Ángeles; Montibeller, G. (2010). "Estructuración de problemas para intervenciones de análisis de decisiones multicriterio". Enciclopedia Wiley de investigación de operaciones y ciencias de la gestión . doi : 10.1002/9780470400531.eorms0683. ISBN 9780470400531.
  3. ^ ab Weistroffer, HR y Li, Y (2016). "Software de análisis de decisiones con múltiples criterios". Capítulo 29 en: Greco, S, Ehrgott, M ​​y Figueira, J, eds, Análisis de decisiones con criterios múltiples: Serie de encuestas sobre el estado del arte , Springer: Nueva York.
  4. ^ ab Amoyal, Justin (2018). "Análisis de decisiones: la encuesta bienal demuestra el avance continuo de herramientas vitales para tomadores de decisiones, gerentes y analistas". OR/MS hoy . doi :10.1287/orms.2018.05.13. S2CID  642562.
  5. ^ Kylili, Angeliki; Christoforou, Elías; Fokaides, París A.; Policarpou, Policarpos (2016). "Análisis multicriterio para la selección de los cultivos energéticos más adecuados: El caso de Chipre". Revista Internacional de Energía Sostenible . 35 (1): 47–58. Código Bib : 2016IJSE...35...47K. doi :10.1080/14786451.2014.898640. S2CID  108512639.
  6. ^ "Toma de decisiones con criterios múltiples - Sociedad internacional sobre MCDM". www.mcdmsociety.org . Archivado desde el original el 3 de octubre de 2017 . Consultado el 26 de abril de 2018 .
  7. ^ "Bienvenido al sitio web del EWG-MCDA". www.cs.put.poznan.pl . Archivado desde el original el 7 de octubre de 2017 . Consultado el 26 de abril de 2018 .
  8. ^ "Copia archivada". Archivado desde el original el 11 de agosto de 2011 . Consultado el 7 de agosto de 2011 .{{cite web}}: Mantenimiento CS1: copia archivada como título ( enlace )
  9. ^ Köksalan, M., Wallenius, J. y Zionts, S. (2011). Toma de decisiones con criterios múltiples: desde la historia temprana hasta el siglo XXI. Singapur: World Scientific. ISBN 9789814335591.{{cite book}}: Mantenimiento CS1: varios nombres: lista de autores ( enlace )
  10. ^ Triantaphyllou, E. (2000). Toma de decisiones multicriterio: un estudio comparativo. Dordrecht, Países Bajos: Kluwer Academic Publishers (ahora Springer). pag. 320.ISBN _ 978-0-7923-6607-2. Archivado desde el original el 24 de junio de 2010.
  11. ^ Un enfoque interactivo para la optimización de criterios múltiples, con una aplicación al funcionamiento de un departamento académico, AM Geoffrion, JS Dyer y A. Feinberg, Management Science, vol. 19, No. 4, Serie de aplicaciones, Parte 1 (diciembre de 1972), págs. 357–368 Publicado por: INFORMS
  12. ^ Köksalan, MM y Sagala, PNS, MM; Sagala, PNS (1995). "Enfoques interactivos para la toma de decisiones alternativas discretas con criterios múltiples con funciones de utilidad monótonas". Ciencias de la gestión . 41 (7): 1158-1171. doi :10.1287/mnsc.41.7.1158.{{cite journal}}: Mantenimiento CS1: varios nombres: lista de autores ( enlace )
  13. ^ Steuer, RE (1986). Optimización de múltiples criterios: teoría, computación y aplicación . Nueva York: John Wiley.
  14. ^ Karasakal, EK y Köksalan, M., E.; Koksalan, M. (2009). "Generación de un subconjunto representativo de la frontera eficiente en la toma de decisiones con criterios múltiples". La investigación de operaciones . 57 : 187–199. doi :10.1287/opre.1080.0581.{{cite journal}}: Mantenimiento CS1: varios nombres: lista de autores ( enlace )
  15. ^ Ehrgott, M. y Gandibleux, X. (2002). "Optimización combinatoria multiobjetivo". Optimización de criterios múltiples, estudios bibliográficos comentados de última generación: 369–444. {{cite journal}}: Citar diario requiere |journal=( ayuda )
  16. ^ Gass, S.; Saaty, T. (1955). "Función objetivo paramétrica Parte II". La investigación de operaciones . 2 (3): 316–319. doi :10.1287/opre.2.3.316.
  17. ^ Wierzbicki, A. (1980). "El uso de objetivos de referencia en la optimización multiobjetivo". Teoría y aplicación de la toma de decisiones con criterios múltiples . Springer, Berlín. vol. 177, págs. 468–486. doi :10.1007/978-3-642-48782-8_32. ISBN 978-3-540-09963-5. {{cite book}}: |journal=ignorado ( ayuda )
  18. ^ Bragge, J.; Korhonen, P.; Wallenius, H.; Wallenius, J. (2010). "Análisis bibliométrico de la toma de decisiones con múltiples criterios/teoría de la utilidad multiatributo". Toma de decisiones con criterios múltiples para sistemas de transporte y energía sostenibles . Springer, Berlín. vol. 634, págs. 259–268. doi :10.1007/978-3-642-04045-0_22. ISBN 978-3-642-04044-3.
  19. ^ Evans, J.; Steuer, R. (1973). "Un método simplex revisado para programas lineales de objetivos múltiples". Programación Matemática . 5 : 54–72. doi :10.1007/BF01580111. S2CID  32037123.
  20. ^ Yu, PL; Zeleny, M. (1975). "El conjunto de todas las soluciones no dominadas en casos lineales y un método simplex multicriterio". Revista de Análisis y Aplicaciones Matemáticas . 49 (2): 430–468. doi : 10.1016/0022-247X(75)90189-4 .
  21. ^ Benayoun, R.; deMontgolfier, J.; Tergny, J.; Larichev, O. (1971). "Programación lineal con múltiples funciones objetivas: método paso a paso (STEM)". Programación Matemática . 1 : 366–375. doi :10.1007/bf01584098. S2CID  29348836.
  22. ^ Geoffrion, A.; Dyer, J.; Feinberg, A. (1972). "Un enfoque interactivo para la optimización multicriterio con una aplicación al funcionamiento de un departamento académico". Ciencias de la gestión . 19 (4 – Parte 1): 357–368. doi :10.1287/mnsc.19.4.357.
  23. ^ Siones, S.; Wallenius, J. (1976). "Un método de programación interactivo para resolver el problema de criterios múltiples". Ciencias de la gestión . 22 (6): 652–663. doi :10.1287/mnsc.22.6.652.
  24. ^ Korhonen, P.; Wallenius, J. (1988). "Una carrera de Pareto". Logística de Investigación Naval . 35 (6): 615–623. doi :10.1002/1520-6750(198812)35:6<615::AID-NAV3220350608>3.0.CO;2-K.
  25. ^ Charnes, A. y Cooper, WW (1961). Modelos de Gestión y Aplicaciones Industriales de la Programación Lineal . Nueva York: Wiley.{{cite book}}: Mantenimiento CS1: varios nombres: lista de autores ( enlace )
  26. ^ Zadeh, LA (junio de 1965). "Conjuntos difusos". Información y Control . San Diego. 8 (3): 338–353. doi : 10.1016/S0019-9958(65)90241-X . ISSN  0019-9958. Zbl  0139.24606. Wikidata  Q25938993.
  27. ^ Keeney, R. y Raiffa, H. (1976). Decisiones con múltiples objetivos: preferencias y compensaciones de valor . Nueva York: Wiley.
  28. ^ Hansen, Pablo; Ombler, Franz (2008). "Un nuevo método para calificar modelos aditivos de valor de atributos múltiples utilizando clasificaciones de alternativas por pares". Revista de análisis de decisiones multicriterio . 15 (3–4): 87–107. doi :10.1002/mcda.428.
  29. ^ Roy, B. (1968). "El método ELECTRE". Revue d'Informatique et de Recherche Opérationelle (RIRO) . 8 : 57–75.
  30. ^ Shaffer, JD (1984). Algunos experimentos en aprendizaje automático utilizando algoritmos genéticos evaluados por vectores, tesis doctoral (doctorado). Nashville: Universidad de Vanderbilt.
  31. ^ Srinivas, N.; Deb, K. (1994). "Optimización multiobjetivo mediante clasificación no dominada en algoritmos genéticos". Computación Evolutiva . 2 (3): 221–248. doi :10.1162/evco.1994.2.3.221. S2CID  13997318.
  32. ^ Deb, K.; Köksalan, M. (2010). "Número especial editorial invitado sobre algoritmos evolutivos multiobjetivos basados ​​en preferencias". Transacciones IEEE sobre computación evolutiva . 14 (5): 669–670. doi :10.1109/TEVC.2010.2070371.
  33. ^ Liu, Sifeng (2017). Análisis de datos grises: métodos, modelos y aplicaciones. Singapur: Springer. págs. 67-104. ISBN 978-981-10-1841-1.
  34. ^ Liu, Sifeng (2013). "Sobre funciones de medida de efecto uniforme y un modelo de decisión de objetivo gris de atributos múltiples ponderado". La revista del sistema Gray . Research Information Ltd. (Reino Unido). 25 (1): 1–11. doi :10.1007/s40815-020-00827-8. S2CID  219090787.
  35. ^ Javed, SA (2020). "Método de análisis de decisión absoluta gris (GADA) para la toma de decisiones en grupo de criterios múltiples en condiciones de incertidumbre". Revista internacional de sistemas difusos . Saltador. 22 (4): 1073–1090. doi :10.1007/s40815-020-00827-8. S2CID  219090787.
  36. ^ Saaty, TL (1980). El proceso de jerarquía analítica: planificación, establecimiento de prioridades, asignación de recursos . Nueva York: McGraw-Hill.
  37. ^ Belton, V y Stewart, TJ (2002). Análisis de decisiones con criterios múltiples: un enfoque integrado , Kluwer: Boston.
  38. ^ ab Munier, Nolberto (2021). Usos y limitaciones del método AHP: un análisis racional y no matemático. Eloy Hontoria. Cham: Springer. ISBN 978-3-030-60392-2. OCLC  1237399430.
  39. ^ Mardani, Abbas; Jusoh, Ahmad; Zavadskas, Edmundas Kazimieras (15 de mayo de 2015). "Técnicas y aplicaciones difusas de toma de decisiones con criterios múltiples: revisión de dos décadas, de 1994 a 2014". Sistemas Expertos con Aplicaciones . 42 (8): 4126–4148. doi :10.1016/j.eswa.2015.01.003.
  40. ^ Mardani, Abbas; Jusoh, Ahmad; Tampoco, Khalil MD; Califa, Zainab; Zakwan, Norhayati; Valipour, Alireza (1 de enero de 2015). "Técnicas de toma de decisiones con criterios múltiples y sus aplicaciones: una revisión de la literatura de 2000 a 2014". Investigación Económica-Ekonomska Istraživanja . 28 (1): 516–571. doi : 10.1080/1331677X.2015.1075139 . ISSN  1331-677X.
  41. ^ Mardani, Abbas; Jusoh, Ahmad; Zavadskas, Edmundas Kazimieras; Cavallaro, Fausto; Khalifah, Zainab (19 de octubre de 2015). "Energía sostenible y renovable: una descripción general de la aplicación de técnicas y enfoques de toma de decisiones con múltiples criterios". Sostenibilidad . 7 (10): 13947–13984. doi : 10.3390/su71013947 .
  42. ^ Mardani, Abbas; Zavadskas, Edmundas Kazimieras; Govindan, Kannan; Amat Senin, Aslan; Jusoh, Ahmad (4 de enero de 2016). "Técnica VIKOR: una revisión sistemática del estado del arte de la literatura sobre metodologías y aplicaciones". Sostenibilidad . 8 (1): 37. doi : 10.3390/su8010037 .
  43. ^ Mardani, Abbas; Zavadskas, Edmundas Kazimieras; Califa, Zainab; Jusoh, Ahmad; Nor, Khalil MD (2 de julio de 2016). "Técnicas de toma de decisiones de criterios múltiples en sistemas de transporte: una revisión sistemática del estado del arte de la literatura". Transporte . 31 (3): 359–385. doi : 10.3846/16484142.2015.1121517 . ISSN  1648-4142.
  44. ^ Mardani, Abbas; Jusoh, Ahmad; Zavadskas, Edmundas Kazimieras; Califa, Zainab; Nor, Khalil MD (3 de septiembre de 2015). "Aplicación de técnicas y enfoques de toma de decisiones con criterios múltiples para evaluar la calidad del servicio: una revisión sistemática de la literatura". Revista de Economía y Gestión Empresarial . 16 (5): 1034–1068. doi : 10.3846/16111699.2015.1095233 . ISSN  1611-1699.
  45. ^ Zavadskas, Edmundas Kazimieras; Mardani, Abbas; Turskis, Zenonas; Jusoh, Ahmad; Tampoco, Khalil MD (1 de mayo de 2016). "Desarrollo del método TOPSIS para resolver problemas complicados de toma de decisiones: una descripción general de la evolución de 2000 a 2015". Revista internacional de tecnología de la información y toma de decisiones . 15 (3): 645–682. doi :10.1142/S0219622016300019. ISSN  0219-6220.
  46. ^ Mardani, Abbas; Zavadskas, Edmundas Kazimieras; Califa, Zainab; Zakuan, Norhayati; Jusoh, Ahmad; Tampoco, Khalil Md; Khoshnoudi, Masoumeh (1 de mayo de 2017). "Una revisión de aplicaciones de toma de decisiones multicriterio para resolver problemas de gestión energética: dos décadas de 1995 a 2015". Reseñas de energías renovables y sostenibles . 71 : 216–256. doi :10.1016/j.rser.2016.12.053.
  47. ^ Zare, Mojtaba; Pahl, Cristina; Rahnama, Hamed; Nilashi, Mehrbakhsh; Mardani, Abbas; Ibrahim, Othman; Ahmadi, Hossein (1 de agosto de 2016). "Enfoque de toma de decisiones multicriterio en e-learning: una revisión y clasificación sistemática". Computación blanda aplicada . 45 : 108-128. doi :10.1016/j.asoc.2016.04.020.
  48. ^ Diedonis, Antanas. "Transformaciones en la economía y los negocios - Vol. 15, No 1 (37), 2016 - Artículo". www.transformaciones.knf.vu.lt . Archivado desde el original el 29 de agosto de 2017 . Consultado el 29 de agosto de 2017 .
  49. ^ Mardani, Abbas; Nilashi, Mehrbakhsh; Zakuan, Norhayati; Loganathan, Nanthakumar; Soheilirad, Somayeh; Saman, Muhamad Zameri Mat; Ibrahim, Othman (1 de agosto de 2017). "Una revisión sistemática y metanálisis de los métodos SWARA y WASPAS: teoría y aplicaciones con desarrollos confusos recientes". Computación blanda aplicada . 57 : 265–292. doi :10.1016/j.asoc.2017.03.045.
  50. ^ Rezaei, Jafar (2015). "Método de toma de decisiones multicriterio mejor-peor". Omega . 53 : 49–57. doi :10.1016/j.omega.2014.11.009.
  51. ^ Rezaei, Jafar (2016). "Método de toma de decisiones multicriterio mejor-peor: algunas propiedades y un modelo lineal". Omega . 64 : 126-130. doi :10.1016/j.omega.2015.12.001.
  52. ^ Sałabun, W. (2015). El método de los objetos característicos: un nuevo enfoque basado en la distancia para problemas de toma de decisiones multicriterio. Revista de análisis de decisiones multicriterio, 22(1-2), 37-50.
  53. ^ Sałabun, W., Piegat, A. (2016). Análisis comparativo de métodos MCDM para la evaluación de la mortalidad en pacientes con síndrome coronario agudo. Revisión de inteligencia artificial. Primero en línea: 3 de septiembre de 2016.
  54. ^ Garnett, HM, Roos, G. y Pike, S. (septiembre de 2008). Evaluación confiable y repetible para determinar el valor y mejorar la eficiencia y eficacia en la educación superior. OCDE, Dirección de Educación, Conferencia del Programa de Gestión Institucional en la Educación Superior [IMHE), Resultados de la Educación Superior: Calidad, Relevancia e Impacto.
  55. ^ Millar, LA, McCallum, J. y Burston, LM (2010). Uso del enfoque de jerarquía de valores conjuntos para medir el valor de la estrategia nacional de gestión de la continencia. Revista de Continencia de Australia y Nueva Zelanda, The, 16(3), 81.
  56. ^ Keshavarz Ghorabaee, M. y col. (2015) "Clasificación de inventarios con criterios múltiples utilizando un nuevo método de evaluación basado en la distancia desde la solución promedio (EDAS) Archivado el 2 de septiembre de 2016 en Wayback Machine ", Informatica, 26(3), 435-451.
  57. ^ Mahmoudi, Amin; Deng, Xiaopeng; Javed, Saad Ahmed; Zhang, Na (enero de 2021). "Selección de proveedores sostenibles en megaproyectos: enfoque de prioridad ordinal gris". Estrategia Empresarial y Medio Ambiente . 30 (1): 318–339. doi :10.1002/bse.2623. S2CID  224917346.
  58. ^ Mahmoudi, Amin; Javed, Saad Ahmed; Mardani, Abbas (16 de marzo de 2021). "Selección de proveedores resistentes mediante el enfoque de prioridad ordinal difusa: toma de decisiones en la era post-COVID". Investigación en Gestión de Operaciones . 15 (1–2): 208–232. doi : 10.1007/s12063-021-00178-z . S2CID  232240914.
  59. ^ Edwards, W.; Barón, FH (1994). "Métodos simples mejorados para la medición de utilidades de múltiples atributos". Comportamiento Organizacional y Procesos de Decisión Humana . 60 : 306–325. doi :10.1006/obhd.1994.1087.
  60. ^ Khazaei, Moein; Ramezani, Mohammad; Padash, Amin; DeTombe, Dorien (8 de mayo de 2021). "Crear valor compartido para rediseñar productos de servicios de TI utilizando SYRCS; diagnosticar y abordar problemas complejos". Sistemas de Información y Gestión de Negocios Electrónicos . 19 (3): 957–992. doi :10.1007/s10257-021-00525-4. ISSN  1617-9846. S2CID  236544531.
  61. ^ Serafim, Opricovic; Gwo-Hshiung, Tzeng (2007). "Método VIKOR ampliado en comparación con métodos de clasificación superior". Revista europea de investigación operativa . 178 (2): 514–529. doi :10.1016/j.ejor.2006.01.020.

Otras lecturas