Aceleración

Tasa de cambio de velocidad

Las carreras de aceleración son un deporte en el que vehículos especialmente construidos compiten para ser los más rápidos en acelerar desde parado.

En mecánica , la aceleración es la tasa de cambio de la velocidad de un objeto con respecto al tiempo. La aceleración es uno de los varios componentes de la cinemática , el estudio del movimiento . Las aceleraciones son cantidades vectoriales (en el sentido de que tienen magnitud y dirección ). ^{[1] [2]} La orientación de la aceleración de un objeto está dada por la orientación de la fuerza neta que actúa sobre ese objeto. La magnitud de la aceleración de un objeto, como se describe en la Segunda Ley de Newton , ^[3] es el efecto combinado de dos causas:

• el equilibrio neto de todas las fuerzas externas que actúan sobre ese objeto: la magnitud es directamente proporcional a esta fuerza neta resultante;
• la masa de ese objeto , dependiendo de los materiales de los que está hecho —la magnitud es inversamente proporcional a la masa del objeto.

La unidad SI para la aceleración es metro por segundo al cuadrado ( m⋅s ⁻² , ). ${\displaystyle \mathrm {\tfrac {m}{s^{2}}} }$

Por ejemplo, cuando un vehículo parte de una posición parada (velocidad cero, en un marco de referencia inercial ) y viaja en línea recta a velocidades crecientes, está acelerando en la dirección de viaje. Si el vehículo gira, se produce una aceleración hacia la nueva dirección y cambia su vector de movimiento. La aceleración del vehículo en su dirección actual de movimiento se llama aceleración lineal (o tangencial durante los movimientos circulares ), la reacción a la cual los pasajeros a bordo experimentan como una fuerza que los empuja hacia sus asientos. Al cambiar de dirección, la aceleración efectiva se llama aceleración radial (o centrípeta durante los movimientos circulares), la reacción a la cual los pasajeros experimentan como una fuerza centrífuga . Si la velocidad del vehículo disminuye, esta es una aceleración en la dirección opuesta del vector de velocidad (matemáticamente un negativo , si el movimiento es unidimensional y la velocidad es positiva), a veces llamada desaceleración ^{[4] [5]} o retardo , y los pasajeros experimentan la reacción a la desaceleración como una fuerza inercial que los empuja hacia adelante. Estas aceleraciones negativas se consiguen a menudo mediante el encendido de retrocohetes en naves espaciales . ^[6] Tanto la aceleración como la desaceleración se tratan de la misma manera, ya que ambas son cambios en la velocidad. Los pasajeros sienten cada una de estas aceleraciones (tangencial, radial, desaceleración) hasta que su velocidad relativa (diferencial) se neutraliza en referencia a la aceleración debida al cambio de velocidad.

Definición y propiedades

Magnitudes cinemáticas de una partícula clásica: masa m , posición r , velocidad v , aceleración a .

Aceleración media

La aceleración es la tasa de cambio de la velocidad. En cualquier punto de una trayectoria, la magnitud de la aceleración está dada por la tasa de cambio de la velocidad tanto en magnitud como en dirección en ese punto. La aceleración verdadera en el tiempo t se encuentra en el límite como intervalo de tiempo Δ t → 0 de Δ v /Δ t .

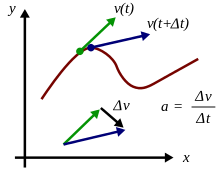
La aceleración media de un objeto durante un período de tiempo es su cambio de velocidad , , dividido por la duración del período, . Matemáticamente, ${\displaystyle \Delta \mathbf {v} }$ ${\displaystyle \Delta t}$ $${\displaystyle {\bar {\mathbf {a} }}={\frac {\Delta \mathbf {v} }{\Delta t}}.}$$

Aceleración instantánea

De abajo hacia arriba :

• una función de aceleración a ( t ) ;
• la integral de la aceleración es la función velocidad v ( t ) ;
• y la integral de la velocidad es la función distancia s ( t ) .

La aceleración instantánea, por su parte, es el límite de la aceleración media en un intervalo infinitesimal de tiempo. En términos de cálculo , la aceleración instantánea es la derivada del vector velocidad con respecto al tiempo: Como la aceleración se define como la derivada de la velocidad, v , con respecto al tiempo t y la velocidad se define como la derivada de la posición, x , con respecto al tiempo, la aceleración puede considerarse como la segunda derivada de x con respecto a t : $${\displaystyle \mathbf {a} =\lim _{{\Delta t}\to 0}{\frac {\Delta \mathbf {v} }{\Delta t}}={\frac {d\mathbf {v} }{dt}}.}$$ $${\displaystyle \mathbf {a} ={\frac {d\mathbf {v} }{dt}}={\frac {d^{2}\mathbf {x} }{dt^{2}}}.}$$

(Aquí y en otros lugares, si el movimiento es en línea recta , las cantidades vectoriales pueden sustituirse por escalares en las ecuaciones).

Por el teorema fundamental del cálculo , se puede ver que la integral de la función aceleración a ( t ) es la función velocidad v ( t ) ; es decir, el área bajo la curva de un gráfico de aceleración vs. tiempo ( a vs. t ) corresponde al cambio de velocidad. Δ v = ∫ a d t . {\displaystyle \mathbf {\Delta v} =\int \mathbf {a} \,dt.}

De la misma manera, la integral de la función jerk j ( t ) , la derivada de la función aceleración, se puede utilizar para encontrar el cambio de aceleración en un tiempo determinado: $${\displaystyle \mathbf {\Delta a} =\int \mathbf {j} \,dt.}$$

Unidades

La aceleración tiene las dimensiones de la velocidad (L/T) dividida por el tiempo, es decir, L T ⁻² . La unidad de aceleración del SI es el metro por segundo al cuadrado (ms ⁻² ); o "metro por segundo por segundo", ya que la velocidad en metros por segundo cambia según el valor de la aceleración, cada segundo.

Otras formas

Un objeto que se mueve en un movimiento circular, como un satélite que orbita alrededor de la Tierra, se acelera debido al cambio de dirección del movimiento, aunque su velocidad puede ser constante. En este caso se dice que experimenta una aceleración centrípeta (dirigida hacia el centro).

La aceleración propia , la aceleración de un cuerpo en relación con una condición de caída libre, se mide mediante un instrumento llamado acelerómetro .

En mecánica clásica , para un cuerpo con masa constante, la aceleración (vectorial) del centro de masas del cuerpo es proporcional al vector de fuerza neta (es decir, la suma de todas las fuerzas) que actúa sobre él ( segunda ley de Newton ): F = m a ⟹ a = F m , {\displaystyle \mathbf {F} =m\mathbf {a} \quad \implies \quad \mathbf {a} ={\frac {\mathbf {F} }{m}},} donde F es la fuerza neta que actúa sobre el cuerpo, m es la masa del cuerpo y a es la aceleración del centro de masas. A medida que las velocidades se acercan a la velocidad de la luz , los efectos relativistas se vuelven cada vez más grandes.

Aceleración tangencial y centrípeta

Péndulo oscilante, con velocidad y aceleración marcadas. Experimenta aceleración tangencial y centrípeta.

Componentes de la aceleración para un movimiento curvo. El componente tangencial a _t se debe al cambio de velocidad de desplazamiento y apunta a lo largo de la curva en la dirección del vector de velocidad (o en la dirección opuesta). El componente normal (también llamado componente centrípeta para el movimiento circular) a _c se debe al cambio de dirección del vector de velocidad y es normal a la trayectoria, apuntando hacia el centro de curvatura de la trayectoria.

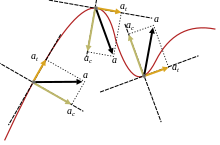
La velocidad de una partícula que se mueve en una trayectoria curva en función del tiempo se puede escribir como: con v ( t ) igual a la velocidad de desplazamiento a lo largo de la trayectoria, y un vector unitario tangente a la trayectoria apuntando en la dirección del movimiento en el momento elegido en el tiempo. Teniendo en cuenta tanto la velocidad cambiante v ( t ) como la dirección cambiante de u _t , la aceleración de una partícula que se mueve en una trayectoria curva se puede escribir utilizando la regla de la cadena de diferenciación ^[7] para el producto de dos funciones del tiempo como: $${\displaystyle \mathbf {v} (t)=v(t){\frac {\mathbf {v} (t)}{v(t)}}=v(t)\mathbf {u} _{\mathrm {t} }(t),}$$ $${\displaystyle \mathbf {u} _{\mathrm {t} }={\frac {\mathbf {v} (t)}{v(t)}}\,,}$$

$${\displaystyle {\begin{alignedat}{3}\mathbf {a} &={\frac {d\mathbf {v} }{dt}}\\&={\frac {dv}{dt}}\mathbf {u} _{\mathrm {t} }+v(t){\frac {d\mathbf {u} _{\mathrm {t} }}{dt}}\\&={\frac {dv}{dt}}\mathbf {u} _{\mathrm {t} }+{\frac {v^{2}}{r}}\mathbf {u} _{\mathrm {n} }\ ,\end{alignedat}}}$$

donde u _n es el vector normal unitario (hacia adentro) a la trayectoria de la partícula (también llamado normal principal ), y r es su radio de curvatura instantáneo basado en el círculo osculador en el tiempo t . Los componentes

${\displaystyle \mathbf {a} _{\mathrm {t} }={\frac {dv}{dt}}\mathbf {u} _{\mathrm {t} }\quad {\text{and}}\quad \mathbf {a} _{\mathrm {c} }={\frac {v^{2}}{r}}\mathbf {u} _{\mathrm {n} }}$

se denominan aceleración tangencial y aceleración normal o radial (o aceleración centrípeta en movimiento circular, véase también movimiento circular y fuerza centrípeta ), respectivamente.

El análisis geométrico de las curvas espaciales tridimensionales, que explica la tangente, la normal (principal) y la binormal, se describe mediante las fórmulas de Frenet-Serret . ^{[8] [9]}

Casos especiales

Aceleración uniforme

Cálculo de la diferencia de velocidad para una aceleración uniforme

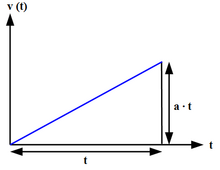
La aceleración uniforme o constante es un tipo de movimiento en el que la velocidad de un objeto cambia en una cantidad igual en cada período de tiempo igual.

Un ejemplo de aceleración uniforme que se cita con frecuencia es el de un objeto en caída libre en un campo gravitatorio uniforme. La aceleración de un cuerpo que cae en ausencia de resistencias al movimiento depende únicamente de la intensidad del campo gravitatorio g (también llamada aceleración debida a la gravedad ). Según la segunda ley de Newton, la fuerza que actúa sobre un cuerpo viene dada por: ${\displaystyle \mathbf {F_{g}} }$ $${\displaystyle \mathbf {F_{g}} =m\mathbf {g} .}$$

Debido a las simples propiedades analíticas del caso de aceleración constante, existen fórmulas simples que relacionan el desplazamiento , las velocidades iniciales y dependientes del tiempo , y la aceleración con el tiempo transcurrido : ^[10] $${\displaystyle {\begin{aligned}\mathbf {s} (t)&=\mathbf {s} _{0}+\mathbf {v} _{0}t+{\tfrac {1}{2}}\mathbf {a} t^{2}=\mathbf {s} _{0}+{\tfrac {1}{2}}\left(\mathbf {v} _{0}+\mathbf {v} (t)\right)t\\\mathbf {v} (t)&=\mathbf {v} _{0}+\mathbf {a} t\\{v^{2}}(t)&={v_{0}}^{2}+2\mathbf {a\cdot } [\mathbf {s} (t)-\mathbf {s} _{0}],\end{aligned}}}$$

dónde

• ${\displaystyle t}$es el tiempo transcurrido,
• ${\displaystyle \mathbf {s} _{0}}$es el desplazamiento inicial desde el origen,
• ${\displaystyle \mathbf {s} (t)}$es el desplazamiento desde el origen en el tiempo , ${\displaystyle t}$
• ${\displaystyle \mathbf {v} _{0}}$es la velocidad inicial,
• ${\displaystyle \mathbf {v} (t)}$es la velocidad en el tiempo , y ${\displaystyle t}$
• ${\displaystyle \mathbf {a} }$es la tasa uniforme de aceleración.

En particular, el movimiento puede descomponerse en dos partes ortogonales, una de velocidad constante y la otra de acuerdo con las ecuaciones anteriores. Como demostró Galileo , el resultado neto es un movimiento parabólico, que describe, por ejemplo, la trayectoria de un proyectil en el vacío cerca de la superficie de la Tierra. ^[11]

Movimiento circular

Vectores cinemáticos en coordenadas polares planas . Observe que la configuración no está restringida al espacio 2D, sino que puede representar el plano osculador en un punto de una curva arbitraria en cualquier dimensión superior.

En el movimiento circular uniforme , es decir, en el movimiento con velocidad constante a lo largo de una trayectoria circular, una partícula experimenta una aceleración resultante del cambio de dirección del vector de velocidad, mientras que su magnitud permanece constante. La derivada de la posición de un punto en una curva con respecto al tiempo, es decir, su velocidad, resulta ser siempre exactamente tangente a la curva, respectivamente ortogonal al radio en este punto. Como en el movimiento uniforme la velocidad en la dirección tangencial no cambia, la aceleración debe ser en dirección radial, apuntando al centro del círculo. Esta aceleración cambia constantemente la dirección de la velocidad para ser tangente en el punto vecino, rotando así el vector de velocidad a lo largo del círculo.

• Para una velocidad dada , la magnitud de esta aceleración causada geométricamente (aceleración centrípeta) es inversamente proporcional al radio del círculo y aumenta con el cuadrado de esta velocidad: a c = v 2 r . {\displaystyle a_{c}={\frac {v^{2}}{r}}\,.} ${\displaystyle v}$ ${\displaystyle r}$
• Para una velocidad angular dada , la aceleración centrípeta es directamente proporcional al radio . Esto se debe a la dependencia de la velocidad con el radio . ${\displaystyle \omega }$ ${\displaystyle r}$ ${\displaystyle v}$ ${\displaystyle r}$ $${\displaystyle v=\omega r.}$$

Expresando el vector de aceleración centrípeta en componentes polares, donde es un vector desde el centro del círculo hasta la partícula con magnitud igual a esta distancia, y considerando la orientación de la aceleración hacia el centro, se obtiene ${\displaystyle \mathbf {r} }$ $${\displaystyle \mathbf {a_{c}} =-{\frac {v^{2}}{|\mathbf {r} |}}\cdot {\frac {\mathbf {r} }{|\mathbf {r} |}}\,.}$$

Como es habitual en las rotaciones, la velocidad de una partícula puede expresarse como una velocidad angular con respecto a un punto a la distancia como ω = v r . {\displaystyle \omega ={\frac {v}{r}}.} ${\displaystyle v}$ ${\displaystyle r}$

De este modo ${\displaystyle \mathbf {a_{c}} =-\omega ^{2}\mathbf {r} \,.}$

Esta aceleración y la masa de la partícula determinan la fuerza centrípeta necesaria , dirigida hacia el centro del círculo, como la fuerza neta que actúa sobre esta partícula para mantenerla en este movimiento circular uniforme. La llamada " fuerza centrífuga ", que parece actuar hacia afuera sobre el cuerpo, es una llamada pseudofuerza experimentada en el marco de referencia del cuerpo en movimiento circular, debido al momento lineal del cuerpo , un vector tangente al círculo de movimiento.

En un movimiento circular no uniforme, es decir, la velocidad a lo largo de la trayectoria curva va cambiando, la aceleración tiene una componente tangencial a la curva que no es cero, y no está confinada a la normal principal , que se dirige al centro del círculo osculador, que determina el radio de la aceleración centrípeta. La componente tangencial está dada por la aceleración angular , es decir, la tasa de cambio de la velocidad angular por el radio . Es decir, ${\displaystyle r}$ ${\displaystyle \alpha }$ ${\displaystyle \alpha ={\dot {\omega }}}$ ${\displaystyle \omega }$ ${\displaystyle r}$ $${\displaystyle a_{t}=r\alpha .}$$

El signo del componente tangencial de la aceleración está determinado por el signo de la aceleración angular ( ), y la tangente siempre está dirigida en ángulo recto al radio vector. ${\displaystyle \alpha }$

Sistemas de coordenadas

En sistemas de coordenadas cartesianas multidimensionales , la aceleración se divide en componentes que corresponden a cada eje dimensional del sistema de coordenadas. En un sistema bidimensional, donde hay un eje x y un eje y, los componentes de aceleración correspondientes se definen como ^[12] El vector de aceleración bidimensional se define entonces como . La magnitud de este vector se encuentra mediante la fórmula de la distancia como En sistemas tridimensionales donde hay un eje z adicional, el componente de aceleración correspondiente se define como El vector de aceleración tridimensional se define como con su magnitud determinada por $${\displaystyle a_{x}=dv_{x}/dt=d^{2}x/dt^{2},}$$ $${\displaystyle a_{y}=dv_{y}/dt=d^{2}y/dt^{2}.}$$ ${\displaystyle {\textbf {a}}=<a_{x},a_{y}>}$ $${\displaystyle |a|={\sqrt {a_{x}^{2}+a_{y}^{2}}}.}$$ $${\displaystyle a_{z}=dv_{z}/dt=d^{2}z/dt^{2}.}$$ ${\displaystyle {\textbf {a}}=<a_{x},a_{y},a_{z}>}$ $${\displaystyle |a|={\sqrt {a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}}.}$$

Relación con la relatividad

Relatividad especial

La teoría especial de la relatividad describe el comportamiento de los objetos que viajan en relación con otros objetos a velocidades cercanas a la de la luz en el vacío. La mecánica newtoniana se revela como una aproximación exacta a la realidad, válida con gran precisión a velocidades más bajas. A medida que las velocidades relevantes aumentan hacia la velocidad de la luz, la aceleración ya no sigue las ecuaciones clásicas.

A medida que la velocidad se acerca a la de la luz, la aceleración producida por una fuerza dada disminuye, volviéndose infinitesimalmente pequeña a medida que se aproxima a la velocidad de la luz; un objeto con masa puede aproximarse a esta velocidad asintóticamente , pero nunca alcanzarla.

Relatividad general

A menos que se conozca el estado de movimiento de un objeto, es imposible distinguir si una fuerza observada se debe a la gravedad o a la aceleración: la gravedad y la aceleración inercial tienen efectos idénticos. Albert Einstein lo llamó principio de equivalencia y dijo que solo los observadores que no sienten ninguna fuerza en absoluto, incluida la fuerza de la gravedad, están justificados para concluir que no están acelerando. ^[13]

Conversiones

Véase también

• Aceleración (geometría diferencial)
• Cuatro vectores : haciendo explícita la conexión entre el espacio y el tiempo
• Aceleración gravitacional
• Inercia
• Órdenes de magnitud (aceleración)
• Choque (mecánica)
• Registrador de datos de vibraciones y choques
  que mide la aceleración en 3 ejes
• Viajes espaciales utilizando aceleración constante
• Fuerza específica

Referencias

1. Bondi, Hermann (1980). Relatividad y sentido común. Courier Dover Publications. pp. 3. ISBN 978-0-486-24021-3.
2. Lehrman, Robert L. (1998). Física de la manera fácil. Serie educativa de Barron. pp. 27. ISBN 978-0-7641-0236-3.
3. Crew, Henry (2008). Los principios de la mecánica . BiblioBazaar, LLC. pág. 43. ISBN 978-0-559-36871-4.
4. P. Smith; RC Smith (1991). Mecánica (2.ª edición ilustrada y reimpresa). John Wiley & Sons. pág. 39. ISBN 978-0-471-92737-2.Extracto de la página 39
5. John D. Cutnell; Kenneth W. Johnson (2014). Física, volumen uno: capítulos 1-17, volumen 1 (1.ª edición ilustrada). John Wiley & Sons. pág. 36. ISBN 978-1-118-83688-0.Extracto de la página 36
6. Raymond A. Serway; Chris Vuille; Jerry S. Faughn (2008). Física universitaria, volumen 10. Cengage. pág. 32. ISBN 9780495386933.
7. Weisstein, Eric W. "Regla de la cadena". Wolfram MathWorld . Wolfram Research . Consultado el 2 de agosto de 2016 .
8. Larry C. Andrews; Ronald L. Phillips (2003). Técnicas matemáticas para ingenieros y científicos. SPIE Press. pág. 164. ISBN 978-0-8194-4506-3.
9. Ch V Ramana Murthy; NC Srinivas (2001). Matemáticas Aplicadas. Nueva Delhi: S. Chand & Co. p. 337. ISBN 978-81-219-2082-7.
10. Keith Johnson (2001). Física para ti: edición revisada del currículo nacional para GCSE (4.ª ed.). Nelson Thornes. pág. 135. ISBN 978-0-7487-6236-1.
11. David C. Cassidy; Gerald James Holton; F. James Rutherford (2002). Entendiendo la física. Birkhäuser. pág. 146. ISBN 978-0-387-98756-9.
12. "Las conferencias Feynman sobre física, vol. I, cap. 9: Leyes de la dinámica de Newton". www.feynmanlectures.caltech.edu . Consultado el 4 de enero de 2024 .
13. Greene, Brian . La trama del cosmos: espacio, tiempo y la textura de la realidad . Vintage. pág. 67. ISBN. 0-375-72720-5.

Enlaces externos

• Calculadora de aceleración Conversor de unidades de aceleración simple
• Calculadora de aceleración La calculadora de conversión de aceleración convierte unidades de metros por segundo cuadrado, kilómetros por segundo cuadrado, milímetros por segundo cuadrado y más con conversión métrica.