Análisis espacial

Técnicas formales que estudian las entidades utilizando sus propiedades topológicas, geométricas o geográficas.

Mapa del Dr. John Snow de Londres , que muestra los grupos de casos de cólera en el brote de cólera de Broad Street de 1854. Este fue uno de los primeros usos del análisis espacial basado en mapas.

El análisis espacial es cualquiera de las técnicas formales que estudian entidades utilizando sus propiedades topológicas , geométricas o geográficas . El análisis espacial incluye una variedad de técnicas que utilizan diferentes enfoques analíticos, especialmente la estadística espacial . Puede aplicarse en campos tan diversos como la astronomía , con sus estudios de la ubicación de las galaxias en el cosmos , o la ingeniería de fabricación de chips, con su uso de algoritmos de "ubicación y ruta" para construir estructuras de cableado complejas. En un sentido más restringido, el análisis espacial es el análisis geoespacial , la técnica aplicada a las estructuras a escala humana, más notablemente en el análisis de datos geográficos . También puede aplicarse a la genómica, como en los datos transcriptómicos .

En el análisis espacial surgen cuestiones complejas, muchas de las cuales no están claramente definidas ni completamente resueltas, pero que forman la base de la investigación actual. La más fundamental de ellas es el problema de definir la ubicación espacial de las entidades que se estudian. La clasificación de las técnicas de análisis espacial es difícil debido a la gran cantidad de campos de investigación diferentes involucrados, los diferentes enfoques fundamentales que se pueden elegir y las múltiples formas que pueden adoptar los datos.

Historia

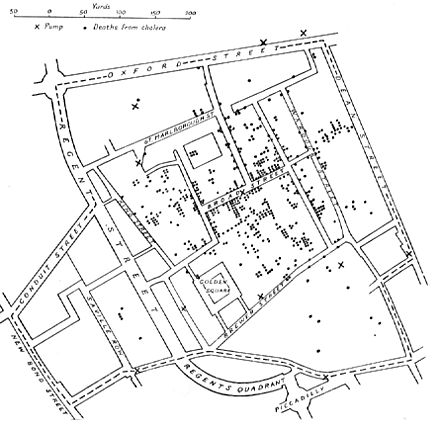
El análisis espacial comenzó con los primeros intentos de cartografía y topografía . La topografía se remonta al menos al año 1400 a. C. en Egipto: las dimensiones de las parcelas imponibles se medían con cuerdas de medición y plomadas. ^[1] Muchos campos han contribuido a su surgimiento en forma moderna. La biología contribuyó a través de estudios botánicos de distribuciones vegetales globales y ubicaciones de plantas locales, estudios etológicos del movimiento animal, estudios ecológicos del paisaje de bloques de vegetación, estudios ecológicos de dinámicas poblacionales espaciales y el estudio de la biogeografía . La epidemiología contribuyó con trabajos tempranos sobre mapeo de enfermedades, en particular el trabajo de John Snow de mapear un brote de cólera, con investigaciones sobre mapeo de la propagación de enfermedades y con estudios de ubicación para la prestación de servicios de salud. Las estadísticas han contribuido en gran medida a través del trabajo en estadísticas espaciales. La economía ha contribuido notablemente a través de la econometría espacial . El sistema de información geográfica es actualmente un contribuyente importante debido a la importancia del software geográfico en la caja de herramientas analíticas modernas. La teledetección ha contribuido ampliamente en el análisis morfométrico y de agrupamiento. La informática ha contribuido enormemente a través del estudio de algoritmos, en particular en la geometría computacional . Las matemáticas siguen proporcionando las herramientas fundamentales para el análisis y para revelar la complejidad del ámbito espacial, por ejemplo, con trabajos recientes sobre fractales e invariancia de escala . El modelado científico proporciona un marco útil para nuevos enfoques. ^{[ cita requerida ]}

Cuestiones fundamentales

El análisis espacial se enfrenta a numerosos problemas fundamentales en la definición de sus objetos de estudio, en la construcción de las operaciones analíticas que se van a utilizar, en el uso de ordenadores para el análisis, en las limitaciones y particularidades de los análisis conocidos y en la presentación de los resultados analíticos. Muchos de estos problemas son objeto de estudio activo en la investigación moderna. ^{[ cita requerida ]}

En el análisis espacial suelen surgir errores comunes, algunos debidos a las matemáticas del espacio, otros a las formas particulares de presentación de los datos espacialmente, otros a las herramientas disponibles. Los datos del censo, dado que protegen la privacidad individual al agregar datos en unidades locales, plantean una serie de problemas estadísticos. La naturaleza fractal de la línea de costa hace que las mediciones precisas de su longitud sean difíciles, si no imposibles. Un software informático que ajuste líneas rectas a la curva de una línea de costa puede calcular fácilmente las longitudes de las líneas que define. Sin embargo, estas líneas rectas pueden no tener un significado inherente en el mundo real, como se demostró en el caso de la línea de costa de Gran Bretaña . ^{[ cita requerida ]}

Estos problemas representan un desafío en el análisis espacial debido al poder de los mapas como medio de presentación. Cuando los resultados se presentan como mapas, la presentación combina datos espaciales que generalmente son precisos con resultados analíticos que pueden ser inexactos, lo que genera la impresión de que los resultados analíticos son más precisos de lo que los datos indicarían. ^[2]

Problemas formales

Problema de límites

Un problema de límites en el análisis es un fenómeno en el que los patrones geográficos se diferencian por la forma y la disposición de los límites que se trazan con fines administrativos o de medición. El problema de los límites se produce debido a la pérdida de vecinos en los análisis que dependen de los valores de los vecinos. Si bien los fenómenos geográficos se miden y analizan dentro de una unidad específica, los datos espaciales idénticos pueden aparecer dispersos o agrupados según el límite colocado alrededor de los datos. En el análisis con datos puntuales, la dispersión se evalúa como dependiente del límite. En el análisis con datos de áreas, las estadísticas deben interpretarse en función del límite.

Problema de unidad de área modificable

Un ejemplo del problema de la unidad de área modificable y la distorsión de los cálculos de tarifas

El problema de la unidad de área modificable (MAUP) es una fuente de sesgo estadístico que puede afectar significativamente los resultados de las pruebas de hipótesis estadísticas . El MAUP afecta los resultados cuando las medidas basadas en puntos de fenómenos espaciales se agregan en particiones espaciales o unidades de área (como regiones o distritos ), como en, por ejemplo, la densidad de población o las tasas de enfermedades . ^{[3] [4]} Los valores de resumen resultantes (por ejemplo, totales, tasas, proporciones, densidades) están influenciados tanto por la forma como por la escala de la unidad de agregación. ^[5]

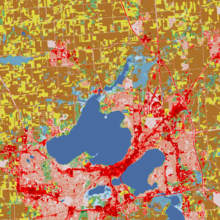
Por ejemplo, los datos del censo pueden agruparse en distritos de condado, áreas censales, áreas de código postal, comisarías de policía o cualquier otra partición espacial arbitraria. Por lo tanto, los resultados de la agrupación de datos dependen de la elección del cartógrafo de qué "unidad de área modificable" utilizar en su análisis. Un mapa coroplético censal que calcule la densidad de población utilizando los límites estatales arrojará resultados radicalmente diferentes a los de un mapa que calcule la densidad basándose en los límites de los condados. Además, los límites de los distritos censales también están sujetos a cambios con el tiempo, ^[6] lo que significa que se debe tener en cuenta la MAUP al comparar los datos pasados ​​con los datos actuales.

Problema de unidad temporal modificable

Diagrama de flujo que ilustra las unidades de tiempo seleccionadas. El gráfico también muestra los tres objetos celestes relacionados con las unidades de tiempo.

El problema de la unidad temporal modificada (MTUP) es una fuente de sesgo estadístico que ocurre en series temporales y análisis espaciales cuando se utilizan datos temporales que se han agregado en unidades temporales . ^{[7] [8]} En tales casos, la elección de una unidad temporal (por ejemplo, días, meses, años) puede afectar los resultados del análisis y generar inconsistencias o errores en las pruebas de hipótesis estadísticas . ^[9]

Problema de promediado del efecto de vecindad

El problema del promedio del efecto de vecindad o NEAP profundiza en los desafíos asociados con la comprensión de la influencia de la agregación de fenómenos a nivel de vecindario en los individuos cuando las exposiciones dependientes de la movilidad influyen en los fenómenos. ^{[10] [11] [12]} El problema confunde el efecto de vecindad , que sugiere que el vecindario de una persona impacta sus características individuales, como la salud. ^{[13] [14]} Se relaciona con el problema de los límites , en el sentido de que los vecindarios delineados utilizados para el análisis pueden no dar cuenta completamente del espacio de actividad de un individuo si los límites son permeables y la movilidad individual cruza los límites. El término fue acuñado por primera vez por Mei-Po Kwan en la revista revisada por pares "International Journal of Environmental Research and Public Health" en 2018. ^{[10] [11]}

Problema del viajante de comercio

Solución del problema del viajante de comercio: la línea negra muestra el bucle más corto posible que conecta cada punto rojo.

En la teoría de la complejidad computacional , el problema del viajante de comercio (TSP) plantea la siguiente pregunta: "Dada una lista de ciudades y las distancias entre cada par de ciudades, ¿cuál es la ruta más corta posible que visita cada ciudad exactamente una vez y regresa a la ciudad de origen?" Es un problema NP-hard en optimización combinatoria , importante en informática teórica e investigación de operaciones .

El problema del comprador viajero , el problema de enrutamiento del vehículo y el problema de la estrella en anillo ^[15] son ​​tres generalizaciones del TSP.

La versión de decisión del TSP (donde, dada una longitud L , la tarea consiste en decidir si el grafo tiene un recorrido cuya longitud sea como máximo L ) pertenece a la clase de problemas NP-completos . Por lo tanto, es posible que el tiempo de ejecución en el peor de los casos para cualquier algoritmo del TSP aumente de manera superpolinómica (pero no más que exponencial ) con el número de ciudades.

El problema se formuló por primera vez en 1930 y es uno de los problemas de optimización que se han estudiado más intensamente. Se utiliza como punto de referencia para muchos métodos de optimización. Aunque el problema es computacionalmente difícil, se conocen muchas heurísticas y algoritmos exactos , de modo que algunos casos con decenas de miles de ciudades se pueden resolver por completo, e incluso los problemas con millones de ciudades se pueden aproximar con una pequeña fracción del 1%. ^[16]

Problema de contexto geográfico incierto

El problema del contexto geográfico incierto o UGCoP es una fuente de sesgo estadístico que puede afectar significativamente los resultados del análisis espacial cuando se trata de datos agregados. ^{[17] [18] [19]} El UGCoP está muy relacionado con el problema de la unidad de área modificable (MAUP), y al igual que el MAUP, surge de cómo dividimos la tierra en unidades de área. ^{[20] [21]} Es causado por la dificultad o imposibilidad de comprender cómo los fenómenos bajo investigación (como las personas dentro de un tramo censal) en diferentes unidades de enumeración interactúan entre unidades de enumeración y fuera de un área de estudio a lo largo del tiempo. ^{[17] [22]} Es particularmente importante considerar el UGCoP dentro de la disciplina de la geografía del tiempo , donde los fenómenos bajo investigación pueden moverse entre unidades de enumeración espaciales durante el período de estudio. ^[18] Los ejemplos de investigación que deben considerar el UGCoP incluyen el acceso a los alimentos y la movilidad humana. ^{[23] [24]}

Esquema y ejemplo de un prisma espacio-temporal utilizando datos de red de tránsito: a la derecha hay un diagrama esquemático de un prisma espacio-temporal y a la izquierda hay un mapa del área de trayectoria potencial para dos presupuestos de tiempo diferentes. ^[25]

El problema del contexto geográfico incierto, o UGCoP, fue acuñado por primera vez por el Dr. Mei-Po Kwan en 2012. ^{[17] [18]} El problema está altamente relacionado con la falacia ecológica , el efecto de borde y el problema de la unidad de área modificable (MAUP) en el sentido de que se relaciona con las unidades agregadas tal como se aplican a los individuos. ^[21] El quid del problema es que los límites que utilizamos para la agregación son arbitrarios y pueden no representar el vecindario real de los individuos dentro de ellos. ^{[20] [21]} Si bien una unidad de enumeración particular, como un tramo censal , contiene la ubicación de una persona, puede cruzar sus límites para trabajar, ir a la escuela y comprar en áreas completamente diferentes. ^{[26] [27]} Por lo tanto, los fenómenos geográficos bajo investigación se extienden más allá del límite delineado. ^{[22] [28] [29]} Diferentes individuos o grupos pueden tener espacios de actividad completamente diferentes , lo que hace que una unidad de enumeración que es relevante para una persona no tenga sentido para otra. ^{[23] [30]} Por ejemplo, un mapa que agrupe a las personas por distritos escolares será más significativo al estudiar una población de estudiantes que la población general. ^[31] El análisis espacial tradicional, por necesidad, trata cada unidad de área discreta como un vecindario autónomo y no considera la actividad diaria de cruzar los límites. ^{[17] [18]}

Problema de Weber

En geometría , el problema de Weber , llamado así por Alfred Weber , es uno de los problemas más famosos de la teoría de la localización . Requiere encontrar un punto en el plano que minimice la suma de los costos de transporte desde este punto hasta n puntos de destino, donde los diferentes puntos de destino están asociados con diferentes costos por unidad de distancia.

El problema de Weber generaliza la mediana geométrica , que supone que los costes de transporte por unidad de distancia son los mismos para todos los puntos de destino, y el problema de calcular el punto de Fermat , la mediana geométrica de tres puntos. Por esta razón, a veces se lo denomina problema de Fermat-Weber, aunque también se ha utilizado el mismo nombre para el problema de la mediana geométrica no ponderada. El problema de Weber se generaliza a su vez mediante el problema de atracción-repulsión, que permite que algunos de los costes sean negativos, de modo que es mejor que haya una mayor distancia desde algunos puntos.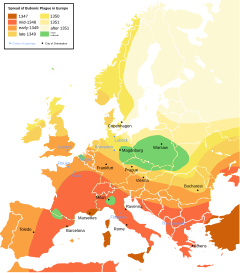

Caracterización espacial

Propagación de la peste bubónica en la Europa medieval. ^{[ cita requerida ]} Los colores indican la distribución espacial de los brotes de peste a lo largo del tiempo.

La definición de la presencia espacial de una entidad restringe el posible análisis que se puede aplicar a esa entidad e influye en las conclusiones finales a las que se puede llegar. Si bien esta propiedad es fundamentalmente cierta en todos los análisis , es particularmente importante en el análisis espacial porque las herramientas para definir y estudiar entidades favorecen caracterizaciones específicas de las entidades que se estudian. Las técnicas estadísticas favorecen la definición espacial de los objetos como puntos porque hay muy pocas técnicas estadísticas que operen directamente sobre elementos de línea, área o volumen. Las herramientas informáticas favorecen la definición espacial de los objetos como elementos homogéneos y separados debido al número limitado de elementos de bases de datos y estructuras computacionales disponibles, y la facilidad con la que se pueden crear estas estructuras primitivas. ^{[ cita requerida ]}

Dependencia espacial

La dependencia espacial es la relación espacial de los valores de las variables (para temas definidos en el espacio, como la lluvia ) o las ubicaciones (para temas definidos como objetos, como las ciudades). La dependencia espacial se mide como la existencia de dependencia estadística en una colección de variables aleatorias , cada una de las cuales está asociada con una ubicación geográfica diferente . La dependencia espacial es importante en aplicaciones donde es razonable postular la existencia de un conjunto correspondiente de variables aleatorias en ubicaciones que no se han incluido en una muestra. Por lo tanto, la lluvia puede medirse en un conjunto de ubicaciones de pluviómetros, y dichas mediciones pueden considerarse como resultados de variables aleatorias, pero la lluvia ocurre claramente en otras ubicaciones y nuevamente sería aleatoria. Debido a que la lluvia exhibe propiedades de autocorrelación , se pueden utilizar técnicas de interpolación espacial para estimar las cantidades de lluvia en ubicaciones cercanas a las ubicaciones medidas. ^[32]

Al igual que con otros tipos de dependencia estadística, la presencia de dependencia espacial generalmente conduce a que las estimaciones de un valor promedio de una muestra sean menos precisas que si las muestras hubieran sido independientes, aunque si existe una dependencia negativa, un promedio de muestra puede ser mejor que en el caso independiente. Un problema diferente al de la estimación de un promedio general es el de la interpolación espacial : aquí el problema es estimar los resultados aleatorios no observados de las variables en ubicaciones intermedias a los lugares donde se realizan las mediciones, en los que existe una dependencia espacial entre las variables aleatorias observadas y no observadas. ^{[ cita requerida ]}

Las herramientas para explorar la dependencia espacial incluyen: correlación espacial , funciones de covarianza espacial y semivariogramas . Los métodos para la interpolación espacial incluyen Kriging , que es un tipo de predicción lineal imparcial óptima . El tema de la dependencia espacial es importante para la geoestadística y el análisis espacial. ^{[ cita requerida ]}

Autocorrelación espacial

La dependencia espacial es la covariación de propiedades dentro del espacio geográfico: las características en ubicaciones próximas parecen estar correlacionadas, ya sea positiva o negativamente. ^[33] La dependencia espacial conduce al problema de la autocorrelación espacial en las estadísticas, ya que, al igual que la autocorrelación temporal, viola las técnicas estadísticas estándar que suponen la independencia entre las observaciones. Por ejemplo, los análisis de regresión que no compensan la dependencia espacial pueden tener estimaciones de parámetros inestables y producir pruebas de significancia poco fiables. Los modelos de regresión espacial (véase más adelante) capturan estas relaciones y no sufren estas debilidades. También es adecuado considerar la dependencia espacial como una fuente de información en lugar de algo que debe corregirse. ^[34]

Los efectos de localización también se manifiestan como heterogeneidad espacial , o la variación aparente de un proceso con respecto a la ubicación en el espacio geográfico. A menos que un espacio sea uniforme e ilimitado, cada ubicación tendrá cierto grado de singularidad en relación con las otras ubicaciones. Esto afecta las relaciones de dependencia espacial y, por lo tanto, el proceso espacial. La heterogeneidad espacial significa que los parámetros generales estimados para todo el sistema pueden no describir adecuadamente el proceso en una ubicación determinada. ^{[ cita requerida ]}

Asociación espacial

La asociación espacial es el grado en el que las cosas están dispuestas de manera similar en el espacio. El análisis de los patrones de distribución de dos fenómenos se realiza mediante la superposición de mapas. Si las distribuciones son similares, entonces la asociación espacial es fuerte, y viceversa. ^[35] En un Sistema de Información Geográfica , el análisis se puede realizar de forma cuantitativa. Por ejemplo, un conjunto de observaciones (como puntos o extraídos de celdas raster) en ubicaciones coincidentes se pueden intersecar y examinar mediante análisis de regresión .

Al igual que la autocorrelación espacial , esta puede ser una herramienta útil para la predicción espacial. En el modelado espacial, el concepto de asociación espacial permite el uso de covariables en una ecuación de regresión para predecir el campo geográfico y, de esta manera, producir un mapa.

La segunda dimensión de la asociación espacial

La segunda dimensión de la asociación espacial (SDA) revela la asociación entre variables espaciales mediante la extracción de información geográfica en ubicaciones fuera de las muestras. La SDA utiliza de manera eficaz la información geográfica faltante fuera de las ubicaciones de las muestras en los métodos de la primera dimensión de la asociación espacial (FDA), que exploran la asociación espacial utilizando observaciones en ubicaciones de muestra. ^[36]

Escalada

La escala de medición espacial es un problema persistente en el análisis espacial; se puede obtener más información en la entrada del tema sobre el problema de la unidad de área modificable (MAUP). Los ecólogos del paisaje desarrollaron una serie de métricas invariantes de escala para aspectos de la ecología que son de naturaleza fractal . ^{[37] En términos más generales, no existe un consenso generalizado sobre ningún método de} análisis independiente de la escala para las estadísticas espaciales. ^{[ cita requerida ]}

Muestreo

El muestreo espacial implica determinar un número limitado de ubicaciones en el espacio geográfico para medir fielmente fenómenos que están sujetos a dependencia y heterogeneidad. ^{[ cita requerida ]} La dependencia sugiere que, dado que una ubicación puede predecir el valor de otra ubicación, no necesitamos observaciones en ambos lugares. Pero la heterogeneidad sugiere que esta relación puede cambiar a lo largo del espacio y, por lo tanto, no podemos confiar en un grado observado de dependencia más allá de una región que puede ser pequeña. Los esquemas básicos de muestreo espacial incluyen el aleatorio, el agrupado y el sistemático. Estos esquemas básicos se pueden aplicar en múltiples niveles en una jerarquía espacial designada (por ejemplo, área urbana, ciudad, vecindario). También es posible explotar datos auxiliares, por ejemplo, utilizando valores de propiedad como guía en un esquema de muestreo espacial para medir el logro educativo y los ingresos. Los modelos espaciales como las estadísticas de autocorrelación, la regresión y la interpolación (ver más abajo) también pueden dictar el diseño de la muestra. ^{[ cita requerida ]}

Errores comunes en el análisis espacial

Las cuestiones fundamentales del análisis espacial dan lugar a numerosos problemas de análisis, entre ellos sesgos, distorsiones y errores evidentes en las conclusiones alcanzadas. Estas cuestiones suelen estar interrelacionadas, pero se han hecho varios intentos de separarlas unas de otras. ^[38]

Longitud

Al analizar la línea costera de Gran Bretaña , Benoit Mandelbrot demostró que ciertos conceptos espaciales son inherentemente absurdos a pesar de la presunción de su validez. Las longitudes en ecología dependen directamente de la escala en la que se miden y experimentan. Así, aunque los topógrafos suelen medir la longitud de un río, esta longitud solo tiene sentido en el contexto de la relevancia de la técnica de medición para la cuestión en estudio. ^[39]

• 
  Gran Bretaña midió utilizando una medición lineal de 200 km.
• 
  Gran Bretaña midió utilizando una medición lineal de 100 km.
• 
  Gran Bretaña midió utilizando una medición lineal de 50 km.

Falacia de localización

La falacia ubicacional se refiere al error debido a la caracterización espacial particular elegida para los elementos de estudio, en particular la elección de la ubicación para la presencia espacial del elemento. ^[39]

Las caracterizaciones espaciales pueden ser simplistas o incluso erróneas. Los estudios sobre seres humanos suelen reducir la existencia espacial de los seres humanos a un único punto, por ejemplo, su dirección de domicilio. Esto puede conducir fácilmente a un análisis deficiente, por ejemplo, cuando se considera la transmisión de enfermedades que puede ocurrir en el trabajo o en la escuela y, por lo tanto, lejos del hogar. ^[39]

La caracterización espacial puede limitar implícitamente el objeto de estudio. Por ejemplo, el análisis espacial de los datos sobre delincuencia se ha vuelto popular recientemente, pero estos estudios sólo pueden describir los tipos particulares de delito que pueden describirse espacialmente. Esto conduce a muchos mapas de asaltos, pero no a ningún mapa de malversación de fondos con consecuencias políticas en la conceptualización del delito y el diseño de políticas para abordar el problema. ^[39]

Falacia atómica

Esto describe errores debidos a tratar los elementos como 'átomos' separados fuera de su contexto espacial. ^[39] La falacia trata de transferir conclusiones individuales a unidades espaciales. ^[40]

Falacia ecológica

La falacia ecológica describe los errores que se producen al realizar análisis sobre datos agregados cuando se intenta llegar a conclusiones sobre las unidades individuales. ^{[39] [41]} Los errores se producen en parte por la agregación espacial. Por ejemplo, un píxel representa las temperaturas superficiales promedio dentro de un área. La falacia ecológica sería suponer que todos los puntos dentro del área tienen la misma temperatura.

Soluciones a los problemas fundamentales

Espacio geográfico

Distancia de Manhattan versus distancia euclidiana: las líneas roja, azul y amarilla tienen la misma longitud (12) tanto en la geometría euclidiana como en la del taxi. En la geometría euclidiana, la línea verde tiene una longitud de 6× √ 2  ≈ 8,48 y es el único camino más corto. En la geometría del taxi, la longitud de la línea verde sigue siendo 12, por lo que no es más corta que cualquier otro camino mostrado.

Existe un espacio matemático siempre que tengamos un conjunto de observaciones y medidas cuantitativas de sus atributos. Por ejemplo, podemos representar los ingresos o los años de educación de los individuos dentro de un sistema de coordenadas donde la ubicación de cada individuo puede especificarse con respecto a ambas dimensiones. La distancia entre individuos dentro de este espacio es una medida cuantitativa de sus diferencias con respecto a los ingresos y la educación. Sin embargo, en el análisis espacial, nos interesan tipos específicos de espacios matemáticos, a saber, el espacio geográfico. En el espacio geográfico, las observaciones corresponden a ubicaciones en un marco de medición espacial que captura su proximidad en el mundo real. Las ubicaciones en un marco de medición espacial a menudo representan ubicaciones en la superficie de la Tierra, pero esto no es estrictamente necesario. Un marco de medición espacial también puede capturar la proximidad con respecto, por ejemplo, al espacio interestelar o dentro de una entidad biológica como un hígado. El principio fundamental es la Primera Ley de Geografía de Tobler : si la interrelación entre entidades aumenta con la proximidad en el mundo real, entonces la representación en el espacio geográfico y la evaluación mediante técnicas de análisis espacial son apropiadas.

La distancia euclidiana entre ubicaciones suele representar su proximidad, aunque esta es solo una posibilidad. Hay una cantidad infinita de distancias además de la euclidiana que pueden respaldar el análisis cuantitativo. Por ejemplo, las distancias de "Manhattan" (o " Taxi ") donde el movimiento está restringido a rutas paralelas a los ejes pueden ser más significativas que las distancias euclidianas en entornos urbanos. Además de las distancias, otras relaciones geográficas como la conectividad (por ejemplo, la existencia o el grado de fronteras compartidas) y la dirección también pueden influir en las relaciones entre entidades. También es posible calcular rutas de costo mínimo a través de una superficie de costo; por ejemplo, esto puede representar la proximidad entre ubicaciones cuando el viaje debe realizarse a través de un terreno accidentado.

Tipos

Los datos espaciales se presentan en muchas variedades y no es fácil llegar a un sistema de clasificación que sea al mismo tiempo exclusivo, exhaustivo, imaginativo y satisfactorio. -- G. Upton y B. Fingelton ^[42]

Análisis de datos espaciales

Los estudios urbanos y regionales se ocupan de grandes tablas de datos espaciales obtenidos a partir de censos y encuestas. Es necesario simplificar la enorme cantidad de información detallada para poder extraer las tendencias principales. El análisis multivariable (o análisis factorial , FA) permite un cambio de variables, transformando las muchas variables del censo, normalmente correlacionadas entre sí, en menos "Factores" o "Componentes Principales" independientes que son, en realidad, los vectores propios de la matriz de correlación de datos ponderados por la inversa de sus valores propios. Este cambio de variables tiene dos ventajas principales:

1. Dado que la información se concentra en los primeros factores nuevos, es posible conservar sólo algunos de ellos y perder sólo una pequeña cantidad de información; al mapearlos se obtienen menos mapas y más significativos.
2. Los factores, en realidad los vectores propios, son ortogonales por construcción, es decir, no están correlacionados. En la mayoría de los casos, el factor dominante (con el valor propio más grande) es el componente social, que separa a los ricos de los pobres en la ciudad. Como los factores no están correlacionados, otros procesos más pequeños que el estatus social, que de otro modo habrían permanecido ocultos, aparecen en el segundo, tercer, etc. factores.

El análisis factorial depende de la medición de distancias entre observaciones: la elección de una métrica significativa es crucial. La métrica euclidiana (análisis de componentes principales), la distancia de chi-cuadrado (análisis de correspondencias) o la distancia de Mahalanobis generalizada (análisis discriminante) se encuentran entre las más utilizadas. ^[43] Se han propuesto modelos más complejos que utilizan comunalidades o rotaciones. ^[44]

El uso de métodos multivariados en el análisis espacial comenzó realmente en la década de 1950 (aunque algunos ejemplos se remontan a principios de siglo) y culminó en la década de 1970, con el aumento de la potencia y la accesibilidad de las computadoras. Ya en 1948, en una publicación seminal, dos sociólogos, Wendell Bell y Eshref Shevky, ^[45] habían demostrado que la mayoría de las poblaciones de las ciudades de los Estados Unidos y del mundo podían representarse con tres factores independientes: 1- el «estatus socioeconómico» que opone distritos ricos y pobres y se distribuye en sectores que corren a lo largo de las autopistas desde el centro de la ciudad, 2- el «ciclo de vida», es decir, la estructura de edad de los hogares, distribuida en círculos concéntricos, y 3- la «raza y etnicidad», que identifica los grupos de migrantes ubicados dentro de la ciudad. En 1961, en un estudio pionero, los geógrafos británicos utilizaron el AF para clasificar las ciudades británicas. ^[46] Brian J Berry, de la Universidad de Chicago, y sus estudiantes hicieron un amplio uso del método, ^[47] aplicándolo a las ciudades más importantes del mundo y exhibiendo estructuras sociales comunes. ^[48] El uso del Análisis Factorial en Geografía, hecho tan fácil por las computadoras modernas, ha sido muy amplio pero no siempre muy sabio. ^[49]

Como los vectores extraídos están determinados por la matriz de datos, no es posible comparar los factores obtenidos de diferentes censos. Una solución consiste en fusionar varias matrices censales en una única tabla que, a continuación, puede analizarse. Sin embargo, esto supone que la definición de las variables no ha cambiado con el tiempo y produce tablas muy grandes, difíciles de manejar. Una solución mejor, propuesta por los psicometristas ^[50] , agrupa los datos en una «matriz cúbica», con tres entradas (por ejemplo, lugares, variables, períodos de tiempo). Un análisis factorial de tres vías produce entonces tres grupos de factores relacionados por una pequeña «matriz central» cúbica. ^[51] Este método, que muestra la evolución de los datos a lo largo del tiempo, no ha sido ampliamente utilizado en geografía. ^[52] Sin embargo , en Los Ángeles ^[53] ha exhibido el papel, tradicionalmente ignorado, del Downtown como centro organizador de toda la ciudad durante varias décadas.

Autocorrelación espacial

Las estadísticas de autocorrelación espacial miden y analizan el grado de dependencia entre las observaciones en un espacio geográfico. Las estadísticas clásicas de autocorrelación espacial incluyen la de Moran ${\displaystyle I}$ , la de Geary ${\displaystyle C}$ , la de Getis y la elipse de desviación estándar. Estas estadísticas requieren medir una matriz de ponderaciones espaciales que refleje la intensidad de la relación geográfica entre las observaciones en un vecindario, por ejemplo, las distancias entre vecinos, las longitudes de la frontera compartida o si caen en una clase direccional específica como "oeste". Las estadísticas clásicas de autocorrelación espacial comparan las ponderaciones espaciales con la relación de covarianza en pares de ubicaciones. La autocorrelación espacial que es más positiva de lo esperado a partir del azar indica la agrupación de valores similares en el espacio geográfico, mientras que la autocorrelación espacial negativa significativa indica que los valores vecinos son más diferentes de lo esperado por casualidad, lo que sugiere un patrón espacial similar a un tablero de ajedrez. ${\displaystyle G}$

Las estadísticas de autocorrelación espacial, como las de Moran y Geary, son globales en el sentido de que estiman el grado general de autocorrelación espacial de un conjunto de datos. La posibilidad de heterogeneidad espacial sugiere que el grado estimado de autocorrelación puede variar significativamente en el espacio geográfico. Las estadísticas de autocorrelación espacial local proporcionan estimaciones desagregadas al nivel de las unidades de análisis espacial, lo que permite la evaluación de las relaciones de dependencia en el espacio. Las estadísticas comparan los vecindarios con un promedio global e identifican regiones locales de fuerte autocorrelación. También hay disponibles versiones locales de las estadísticas y . ${\displaystyle I}$ ${\displaystyle C}$ ${\displaystyle G}$ ${\displaystyle I}$ ${\displaystyle C}$

Heterogeneidad espacial

Cobertura terrestre que rodea Madison, Wisconsin. Los campos están coloreados de amarillo y marrón, el agua está coloreada de azul y las superficies urbanas están coloreadas de rojo.

La heterogeneidad espacial es una propiedad que generalmente se atribuye a un paisaje o a una población . Se refiere a la distribución desigual de diversas concentraciones de cada especie dentro de un área. Un paisaje con heterogeneidad espacial tiene una mezcla de concentraciones de múltiples especies de plantas o animales (biológicas), o de formaciones del terreno (geológicas), o características ambientales (por ejemplo, lluvia, temperatura, viento) que llenan su área. Una población que muestra heterogeneidad espacial es aquella en la que diversas concentraciones de individuos de esta especie se distribuyen de manera desigual en un área; casi sinónimo de "distribución irregular".

Interacción espacial

Los modelos de interacción espacial o " modelos de gravedad " estiman el flujo de personas, material o información entre ubicaciones en el espacio geográfico. Los factores pueden incluir variables propulsoras del origen, como la cantidad de viajeros en áreas residenciales, variables de atractivo del destino, como la cantidad de espacio de oficina en áreas de empleo, y relaciones de proximidad entre las ubicaciones medidas en términos como la distancia en automóvil o el tiempo de viaje. Además, se deben identificar las relaciones topológicas o conectivas entre áreas, en particular considerando la relación a menudo conflictiva entre la distancia y la topología; por ejemplo, dos vecindarios espacialmente cercanos pueden no mostrar ninguna interacción significativa si están separados por una autopista. Después de especificar las formas funcionales de estas relaciones, el analista puede estimar los parámetros del modelo utilizando datos de flujo observados y técnicas de estimación estándar, como los mínimos cuadrados ordinarios o la máxima verosimilitud. Las versiones de destinos competitivos de los modelos de interacción espacial incluyen la proximidad entre los destinos (u orígenes) además de la proximidad origen-destino; esto captura los efectos de la agrupación de destinos (origen) en los flujos.

Interpolación espacial

Los métodos de interpolación espacial estiman las variables en ubicaciones no observadas en el espacio geográfico en función de los valores en las ubicaciones observadas. Los métodos básicos incluyen la ponderación de la distancia inversa : esto atenúa la variable a medida que disminuye la proximidad a la ubicación observada. Kriging es un método más sofisticado que interpola en el espacio de acuerdo con una relación de desfase espacial que tiene componentes sistemáticos y aleatorios. Esto puede dar cabida a una amplia gama de relaciones espaciales para los valores ocultos entre las ubicaciones observadas. Kriging proporciona estimaciones óptimas dada la relación de desfase hipotética, y las estimaciones de error se pueden mapear para determinar si existen patrones espaciales.

Regresión espacial

Los métodos de regresión espacial capturan la dependencia espacial en el análisis de regresión , evitando problemas estadísticos como parámetros inestables y pruebas de significancia poco confiables, así como proporcionando información sobre las relaciones espaciales entre las variables involucradas. Dependiendo de la técnica específica, la dependencia espacial puede entrar en el modelo de regresión como relaciones entre las variables independientes y las dependientes, entre las variables dependientes y un rezago espacial de sí misma, o en los términos de error. La regresión ponderada geográficamente (GWR) es una versión local de la regresión espacial que genera parámetros desagregados por las unidades espaciales de análisis. ^[54] Esto permite la evaluación de la heterogeneidad espacial en las relaciones estimadas entre las variables independientes y dependientes. El uso del modelado jerárquico bayesiano ^[55] junto con los métodos de Monte Carlo de cadena de Markov (MCMC) han demostrado recientemente ser eficaces en el modelado de relaciones complejas utilizando Poisson-Gamma-CAR, Poisson-lognormal-SAR o modelos logit sobredispersados. Los paquetes estadísticos para implementar dichos modelos bayesianos utilizando MCMC incluyen WinBugs , CrimeStat y muchos paquetes disponibles a través del lenguaje de programación R. ^[56]

Los procesos estocásticos espaciales, como los procesos gaussianos , también se están utilizando cada vez más en el análisis de regresión espacial. Las versiones basadas en modelos de GWR, conocidas como modelos de coeficientes de variación espacial, se han aplicado para realizar inferencias bayesianas. ^[55] Los procesos estocásticos espaciales pueden convertirse en modelos de procesos gaussianos escalables y computacionalmente eficaces, como los procesos predictivos gaussianos ^[57] y los procesos gaussianos del vecino más cercano (NNGP). ^[58]

Redes neuronales espaciales

Las redes neuronales espaciales (SNN) constituyen una supercategoría de redes neuronales personalizadas (NN) para representar y predecir fenómenos geográficos. Generalmente mejoran tanto la precisión estadística como la confiabilidad de las NN a-espaciales/clásicas siempre que manejan conjuntos de datos geoespaciales , y también de los otros modelos espaciales (estadísticos) (por ejemplo, modelos de regresión espacial) siempre que las variables de los conjuntos de datos geoespaciales representen relaciones no lineales . ^{[59] [60] [61]} Ejemplos de SNN son las redes neuronales espaciales OSFA, SVANN y GWNN.

Simulación y modelado

Los modelos de interacción espacial son agregados y de arriba hacia abajo: especifican una relación de gobierno general para el flujo entre ubicaciones. Esta característica también la comparten los modelos urbanos, como los basados ​​en programación matemática, los flujos entre sectores económicos o la teoría de la renta de oferta. Una perspectiva de modelado alternativa es representar el sistema en el nivel más alto posible de desagregación y estudiar el surgimiento de abajo hacia arriba de patrones y relaciones complejos a partir del comportamiento y las interacciones a nivel individual. ^{[ cita requerida ]}

La teoría de sistemas adaptativos complejos aplicada al análisis espacial sugiere que las interacciones simples entre entidades proximales pueden conducir a entidades espaciales intrincadas, persistentes y funcionales a niveles agregados. Dos métodos de simulación espacial fundamentalmente son los autómatas celulares y el modelado basado en agentes. El modelado de autómatas celulares impone un marco espacial fijo, como celdas de cuadrícula, y especifica reglas que dictan el estado de una celda en función de los estados de sus celdas vecinas. A medida que avanza el tiempo, surgen patrones espaciales a medida que las celdas cambian de estado en función de sus vecinas; esto altera las condiciones para períodos de tiempo futuros. Por ejemplo, las celdas pueden representar ubicaciones en un área urbana y sus estados pueden ser diferentes tipos de uso de la tierra. Los patrones que pueden surgir de las interacciones simples de los usos de la tierra locales incluyen distritos de oficinas y expansión urbana . El modelado basado en agentes utiliza entidades de software (agentes) que tienen un comportamiento determinado (objetivos) y pueden reaccionar, interactuar y modificar su entorno mientras buscan sus objetivos. A diferencia de las celdas en los autómatas celulares, los simulistas pueden permitir que los agentes sean móviles con respecto al espacio. Por ejemplo, se podría modelar el flujo y la dinámica del tráfico utilizando agentes que representan vehículos individuales que intentan minimizar el tiempo de viaje entre orígenes y destinos específicos. Mientras buscan tiempos de viaje mínimos, los agentes deben evitar colisiones con otros vehículos que también buscan minimizar sus tiempos de viaje. Los autómatas celulares y el modelado basado en agentes son estrategias de modelado complementarias. Pueden integrarse en un sistema de autómatas geográficos común donde algunos agentes son fijos mientras que otros son móviles.

La calibración desempeña un papel fundamental en los enfoques de simulación y modelado tanto de CA como de ABM. Los enfoques iniciales de CA propusieron enfoques de calibración robustos basados ​​en métodos estocásticos de Monte Carlo. ^{[62] [63]} Los enfoques de ABM se basan en las reglas de decisión de los agentes (en muchos casos extraídas de métodos de base de investigación cualitativa como cuestionarios). ^[64] Los algoritmos de aprendizaje automático recientes calibran utilizando conjuntos de entrenamiento, por ejemplo, para comprender las cualidades del entorno construido. ^[65]

Geoestadística de puntos múltiples (MPS)

El análisis espacial de un modelo geológico conceptual es el objetivo principal de cualquier algoritmo MPS. El método analiza las estadísticas espaciales del modelo geológico, denominadas imagen de entrenamiento, y genera realizaciones de los fenómenos que respetan esas estadísticas de puntos múltiples de entrada.

Un algoritmo MPS reciente utilizado para llevar a cabo esta tarea es el método basado en patrones de Honarkhah. ^[66] En este método, se emplea un enfoque basado en la distancia para analizar los patrones en la imagen de entrenamiento. Esto permite la reproducción de las estadísticas de puntos múltiples y las características geométricas complejas de la imagen de entrenamiento. Cada salida del algoritmo MPS es una realización que representa un campo aleatorio. En conjunto, se pueden utilizar varias realizaciones para cuantificar la incertidumbre espacial.

Uno de los métodos más recientes es el presentado por Tahmasebi et al. ^[67], que utiliza una función de correlación cruzada para mejorar la reproducción de patrones espaciales. Llaman a su método de simulación MPS algoritmo CCSIM. Este método es capaz de cuantificar la conectividad espacial, la variabilidad y la incertidumbre. Además, el método no es sensible a ningún tipo de datos y es capaz de simular escenarios tanto categóricos como continuos. El algoritmo CCSIM se puede utilizar para cualquier sistema estacionario, no estacionario y multivariado y puede proporcionar un modelo de atractivo visual de alta calidad., ^{[68] [69]}

Análisis geoespacial e hidroespacial

El análisis geoespacial e hidroespacial , o simplemente análisis espacial , ^[70] es un enfoque para aplicar el análisis estadístico y otras técnicas analíticas a datos que tienen un aspecto geográfico o espacial. Este análisis normalmente emplearía software capaz de generar mapas, procesar datos espaciales y aplicar métodos analíticos a conjuntos de datos terrestres o geográficos , incluido el uso de sistemas de información geográfica y geomática . ^{[71] [72] [73]}

Uso del sistema de información geográfica

Los sistemas de información geográfica (SIG), un amplio dominio que proporciona una variedad de capacidades diseñadas para capturar, almacenar, manipular, analizar, gestionar y presentar todo tipo de datos geográficos, utilizan análisis geoespacial e hidroespacial en una variedad de contextos, operaciones y aplicaciones.

Aplicaciones básicas

El análisis geoespacial e hidroespacial, utilizando SIG , fue desarrollado para problemas en las ciencias ambientales y de la vida, en particular ecología , geología y epidemiología . Se ha extendido a casi todas las industrias, incluidas la defensa, la inteligencia, los servicios públicos, los recursos naturales (es decir, petróleo y gas, silvicultura, etc.), las ciencias sociales, la medicina y la seguridad pública (es decir, la gestión de emergencias y la criminología), la reducción y gestión del riesgo de desastres (DRRM) y la adaptación al cambio climático (CCA). Las estadísticas espaciales generalmente resultan principalmente de la observación en lugar de la experimentación. El hidroespacial se utiliza particularmente para el lado acuático y los miembros relacionados con la superficie del agua, la columna, el fondo, el subsuelo y las zonas costeras.

Operaciones básicas

Los SIG basados ​​en vectores suelen estar relacionados con operaciones como la superposición de mapas (combinar dos o más mapas o capas de mapas según reglas predefinidas), el almacenamiento en búfer simple (identificar regiones de un mapa dentro de una distancia específica de una o más entidades, como ciudades, carreteras o ríos) y operaciones básicas similares. Esto refleja (y se refleja en) el uso del término análisis espacial dentro del Consorcio Geoespacial Abierto ( OGC ) "especificaciones de entidades simples". Para los SIG basados ​​en ráster, ampliamente utilizados en las ciencias ambientales y la teledetección, esto generalmente significa una serie de acciones aplicadas a las celdas de la cuadrícula de uno o más mapas (o imágenes) que a menudo implican filtrado y/o operaciones algebraicas (álgebra de mapas). Estas técnicas implican el procesamiento de una o más capas ráster según reglas simples que dan como resultado una nueva capa de mapa, por ejemplo, reemplazando cada valor de celda con alguna combinación de los valores de sus vecinos, o calculando la suma o diferencia de valores de atributos específicos para cada celda de la cuadrícula en dos conjuntos de datos ráster coincidentes. Las estadísticas descriptivas, como los recuentos de células, las medias, las varianzas, los máximos, los mínimos, los valores acumulados, las frecuencias y una serie de otras medidas y cálculos de distancia también se incluyen a menudo en este término genérico de análisis espacial. El análisis espacial incluye una gran variedad de técnicas estadísticas ( estadísticas descriptivas, exploratorias y explicativas ) que se aplican a los datos que varían espacialmente y que pueden variar con el tiempo. Algunas técnicas estadísticas más avanzadas incluyen Getis-ord Gi* o Anselin Local Moran's I, que se utilizan para determinar patrones de agrupamiento de datos referenciados espacialmente.

Operaciones avanzadas

El análisis geoespacial e hidroespacial va más allá de las operaciones de mapeo 2D y 3D y las estadísticas espaciales. Es multidimensional y también temporal e incluye:

• Análisis de superficies, en particular el análisis de las propiedades de las superficies físicas, como el gradiente , el aspecto y la visibilidad , y el análisis de “campos” de datos similares a superficies;
• Análisis de redes: examen de las propiedades de las redes naturales y artificiales para comprender el comportamiento de los flujos dentro y alrededor de dichas redes; y análisis de ubicación. El análisis de redes basado en SIG se puede utilizar para abordar una amplia gama de problemas prácticos, como la selección de rutas y la ubicación de instalaciones (temas centrales en el campo de la investigación de operaciones ), y problemas que involucran flujos como los que se encuentran en la investigación hidroespacial, hidrológica y de transporte. En muchos casos, los problemas de ubicación se relacionan con las redes y, como tales, se abordan con herramientas diseñadas para este propósito, pero en otros, las redes existentes pueden tener poca o ninguna relevancia o pueden ser poco prácticas para incorporarlas dentro del proceso de modelado. Los problemas que no están específicamente restringidos a la red, como el trazado de nuevas carreteras o tuberías, la ubicación de almacenes regionales, el posicionamiento de antenas de telefonía móvil o la selección de sitios de atención médica comunitaria rural, se pueden analizar de manera efectiva (al menos inicialmente) sin referencia a las redes físicas existentes. El análisis de ubicación "en el plano" también es aplicable cuando no se dispone de conjuntos de datos de red adecuados, o son demasiado grandes o costosos para ser utilizados, o cuando el algoritmo de ubicación es muy complejo o implica el examen o la simulación de un número muy grande de configuraciones alternativas.
• Geovisualización : creación y manipulación de imágenes, mapas, diagramas, gráficos, vistas 3D y sus conjuntos de datos tabulares asociados. Los paquetes SIG ofrecen cada vez más una gama de estas herramientas, que proporcionan vistas estáticas o rotatorias, superposición de imágenes sobre representaciones de superficies 2,5D, animaciones y recorridos, vinculación y pincelado dinámicos y visualizaciones espacio-temporales. Esta última clase de herramientas es la menos desarrollada, lo que refleja en parte la gama limitada de conjuntos de datos compatibles adecuados y el conjunto limitado de métodos analíticos disponibles, aunque este panorama está cambiando rápidamente. Todas estas funciones amplían las herramientas básicas utilizadas en el análisis espacial a lo largo del proceso analítico (exploración de datos, identificación de patrones y relaciones, construcción de modelos y comunicación de resultados).

Computación geoespacial e hidroespacial móvil

Tradicionalmente, la computación geoespacial e hidroespacial se ha realizado principalmente en computadoras personales (PC) o servidores. Sin embargo, debido a las crecientes capacidades de los dispositivos móviles, la computación geoespacial en dispositivos móviles es una tendencia de rápido crecimiento. ^[74] La naturaleza portátil de estos dispositivos, así como la presencia de sensores útiles, como los receptores del Sistema Global de Navegación por Satélite (GNSS) y los sensores de presión barométrica, los hacen útiles para capturar y procesar información geoespacial e hidroespacial en el campo. Además del procesamiento local de información geoespacial en dispositivos móviles, otra tendencia creciente es la computación geoespacial basada en la nube. En esta arquitectura, los datos se pueden recopilar en el campo utilizando dispositivos móviles y luego transmitirlos a servidores basados ​​en la nube para su posterior procesamiento y almacenamiento final. De manera similar, la información geoespacial e hidroespacial se puede poner a disposición de dispositivos móviles conectados a través de la nube, lo que permite el acceso a vastas bases de datos de información geoespacial e hidroespacial en cualquier lugar donde haya una conexión de datos inalámbrica disponible.

Ciencia de la información geográfica y análisis espacial

Este mapa de flujo de la desafortunada marcha de Napoleón sobre Moscú es un ejemplo temprano y célebre de geovisualización. Muestra la dirección del ejército a medida que avanzaba, los lugares por los que pasaban las tropas, el tamaño del ejército a medida que las tropas morían de hambre y heridas, y las gélidas temperaturas que experimentaron.

Los sistemas de información geográfica (SIG) y la ciencia de la información geográfica subyacente que hace avanzar estas tecnologías tienen una fuerte influencia en el análisis espacial. La creciente capacidad de capturar y manejar datos geográficos significa que el análisis espacial se está produciendo en entornos cada vez más ricos en datos. Los sistemas de captura de datos geográficos incluyen imágenes captadas por teledetección, sistemas de monitoreo ambiental como sistemas de transporte inteligentes y tecnologías que reconocen la ubicación como dispositivos móviles que pueden informar la ubicación casi en tiempo real. Los SIG proporcionan plataformas para gestionar estos datos, calcular relaciones espaciales como distancia, conectividad y relaciones direccionales entre unidades espaciales y visualizar tanto los datos brutos como los resultados analíticos espaciales dentro de un contexto cartográfico. Los subtipos incluyen:

• La geovisualización (GVis) combina la visualización científica con la cartografía digital para respaldar la exploración y el análisis de datos e información geográficos, incluidos los resultados del análisis o la simulación espacial. La GVis aprovecha la orientación humana hacia el procesamiento de información visual en la exploración, el análisis y la comunicación de datos e información geográficos. A diferencia de la cartografía tradicional, la GVis suele ser tridimensional o cuatridimensional (esta última incluye el tiempo) e interactiva con el usuario.
• El descubrimiento de conocimiento geográfico (GKD) es el proceso centrado en el ser humano de aplicar herramientas computacionales eficientes para explorar bases de datos espaciales masivas . GKD incluye la minería de datos geográficos , pero también abarca actividades relacionadas como la selección de datos, la limpieza y el preprocesamiento de datos, y la interpretación de los resultados. GVis también puede cumplir un papel central en el proceso de GKD. GKD se basa en la premisa de que las bases de datos masivas contienen patrones interesantes (válidos, novedosos, útiles y comprensibles) que las técnicas analíticas estándar no pueden encontrar. GKD puede servir como un proceso de generación de hipótesis para el análisis espacial, produciendo patrones y relaciones tentativos que deben confirmarse utilizando técnicas analíticas espaciales.
• Los sistemas de apoyo a la toma de decisiones espaciales (SDSS) toman datos espaciales existentes y utilizan una variedad de modelos matemáticos para hacer proyecciones hacia el futuro. Esto permite a los planificadores urbanos y regionales probar las decisiones de intervención antes de su implementación. ^[75]

Véase también

Temas generales

• Análisis de buffer
• Cartografía
• Aleatoriedad espacial completa
• Conceptos y técnicas de la geografía moderna
• Análisis de distancia de costo
• Cuatro tradiciones de la geografía
• Geocomputación
• Inteligencia geoespacial
• Modelado predictivo geoespacial
• Modelo de nueve intersecciones dimensionalmente extendido (DE-9IM)
• Ciencia de la información geográfica
• Estadística matemática
• Problema de unidad de área modificable
• Problema de unidad temporal modificable
• Problema de promediado del efecto de vecindad
• Proceso de puntos
• Análisis de proximidad
• Estadísticas descriptivas espaciales
• Relación espacial
• Geografía técnica
• Análisis del terreno
• Primera ley de geografía de Tobler
• Segunda ley de geografía de Tobler
• Lista de software de análisis espacial

Aplicaciones específicas

• Problema de límites (en análisis espacial)
• Análisis del dominio de extrapolación
• Análisis espacial arquitectónico difuso
• Segmentación geodemográfica
• Sistemas de información geográfica
• Geoinformática
• Geoestadística
• Permeabilidad (planificación espacial y del transporte)
• Econometría espacial
• Epidemiología espacial
• Análisis de idoneidad
• Análisis de cuenca visual

Referencias

1. La historia de la topografía. Consultado el 17 de diciembre de 2020. https://info.courthousedirect.com/blog/history-of-land-surveying
2. Mark Monmonier Cómo mentir con mapas University of Chicago Press, 1996.
3. Openshaw, Stan (1983). El problema de la unidad de área modificable (PDF) . Geo Books. ISBN 0-86094-134-5.
4. Chen, Xiang; Ye, Xinyue; Widener, Michael J.; Delmelle, Eric; Kwan, Mei-Po; Shannon, Jerry; Racine, Racine F.; Adams, Aaron; Liang, Lu; Peng, Jia (27 de diciembre de 2022). "Una revisión sistemática del problema de la unidad de área modificable (MAUP) en la investigación ambiental de alimentos comunitarios". Informática urbana . 1 (1): 22. Bibcode :2022UrbIn...1...22C. doi : 10.1007/s44212-022-00021-1 . S2CID  255206315.
5. "MAUP | Definición – Diccionario GIS de soporte de Esri". support.esri.com . Consultado el 9 de marzo de 2017 .
6. Geografía, Oficina del Censo de los Estados Unidos. "Notas sobre cambios en los límites geográficos". www.census.gov . Consultado el 24 de febrero de 2017 .
7. Cheng, Tao; Adepeju, Monsuru; Preis, Tobias (27 de junio de 2014). "Problema de unidad temporal modificable (MTUP) y su efecto en la detección de cúmulos espacio-temporales". PLOS ONE . ​​9 (6): e100465. Bibcode :2014PLoSO...9j0465C. doi : 10.1371/journal.pone.0100465 . PMC 4074055 . PMID  24971885. 
8. Jong, R. de; Bruin, S. de (5 de enero de 2012). "Tendencias lineales en series temporales de vegetación estacional y el problema de la unidad temporal modificable". Biogeosciences . 9 (1): 71–77. Bibcode :2012BGeo....9...71D. doi : 10.5194/bg-9-71-2012 .
9. Deckard, Mica; Schnell, Cory (22 de octubre de 2022). "La (in)estabilidad temporal de los puntos calientes de delitos violentos entre meses y el problema de la unidad temporal modificable". Crime & Delinquency . 69 (6–7): 1312–1335. doi :10.1177/00111287221128483.
10. Kwan, Mei-Po (2018). "El problema del promedio del efecto del vecindario (NEAP): un factor de confusión elusivo del efecto del vecindario". Int J Environ Res Public Health . 15 (9): 1841. doi : 10.3390/ijerph15091841 . PMC 6163400 . PMID  30150510. 
11. Kwan, Mei-Po (2023). "La movilidad humana y el problema del promedio del efecto del vecindario (NEAP)". En Li, Bin; Xun, Shi; A-Xing, Zhu; Wang, Cuizhen; Lin, Hui (eds.). Nuevo pensamiento en la ciencia de los sistemas de información geográfica . Springer. págs. 95–101. doi :10.1007/978-981-19-3816-0_11. ISBN . 978-981-19-3818-4. Recuperado el 7 de octubre de 2023 .
12. Xu, Tiantian; Wang, Shiyi; Liu, Qing; Kim, Junghwan; Zhang, Jingyi; Ren, Yiwen; Ta, Na; Wang, Xiaoliang; Wu, Jiayu (agosto de 2023). "Diferencias de exposición al color de la vegetación a nivel comunitario e individual: un marco explicativo basado en el problema del promedio del efecto del vecindario". Silvicultura urbana y ecologización urbana . 86 . Código Bibliográfico :2023UFUG...8628001X. doi :10.1016/j.ufug.2023.128001.
13. Ham, Maarten van; Manley, David (2012). "La investigación sobre los efectos del vecindario en una encrucijada. Diez desafíos para la investigación futura Introducción". Environment and Planning A: Economy and Space . 44 (12): 2787–2793. doi :10.1068/a4543.
14. Parry, Marc (5 de noviembre de 2012). "El efecto del barrio". THE CHRONICLE REVIEW. The Chronicle of Higher Education . Consultado el 7 de octubre de 2023 .
15. Labbé, Martine; Laporte, Gilbert; Martín, Inmaculada Rodríguez; González, Juan José Salazar (mayo de 2004). "El problema de la estrella anillo: análisis poliédrico y algoritmo exacto". Redes . 43 (3): 177–189. doi :10.1002/net.10114. ISSN  0028-3045.
16. Véase el problema de la gira mundial del TSP, que ya se ha resuelto con un margen de error del 0,05 % de la solución óptima. [1]
17. Kwan, Mei-Po (2012). "El problema del contexto geográfico incierto". Anales de la Asociación de Geógrafos Estadounidenses . 102 (5): 958–968. doi :10.1080/00045608.2012.687349. S2CID  52024592.
18. Kwan, Mei-Po (2012). "Cómo los SIG pueden ayudar a abordar el problema del contexto geográfico incierto en la investigación en ciencias sociales". Anales de SIG . 18 (4): 245–255. Código Bibliográfico :2012AnGIS..18..245K. doi :10.1080/19475683.2012.727867. S2CID  13215965 . Consultado el 4 de enero de 2023 .
19. Matthews, Stephen A. (2017). Enciclopedia internacional de geografía: personas, la Tierra, medio ambiente y tecnología: problema de contexto geográfico incierto. Wiley. doi :10.1002/9781118786352.wbieg0599.
20. Openshaw, Stan (1983). El problema de la unidad aérea modificable (PDF) . GeoBooks. ISBN 0-86094-134-5.
21. Chen, Xiang; Ye, Xinyue; Widener, Michael J.; Delmelle, Eric; Kwan, Mei-Po; Shannon, Jerry; Racine, Racine F.; Adams, Aaron; Liang, Lu; Peng, Jia (27 de diciembre de 2022). "Una revisión sistemática del problema de la unidad de área modificable (MAUP) en la investigación ambiental de alimentos comunitarios". Informática urbana . 1 (1): 22. Bibcode :2022UrbIn...1...22C. doi : 10.1007/s44212-022-00021-1 . S2CID  255206315.
22. Gao, Fei; Kihal, Wahida; Meur, Nolwenn Le; Souris, Marc; Deguen, Séverine (2017). "¿El efecto de borde impacta en la medida de accesibilidad espacial a los proveedores de atención médica?". Revista Internacional de Geografía de la Salud . 16 (1): 46. doi : 10.1186/s12942-017-0119-3 . PMC 5725922 . PMID  29228961. 
23. Chen, Xiang; Kwan, Mei-Po (2015). "Incertidumbres contextuales, movilidad humana y entorno alimentario percibido: el problema del contexto geográfico incierto en la investigación sobre el acceso a los alimentos". Revista estadounidense de salud pública . 105 (9): 1734–1737. doi :10.2105/AJPH.2015.302792. PMC 4539815 . PMID  26180982. 
24. Zhou, Xingang; Liu, Jianzheng; Gar On Yeh, Anthony; Yue, Yang; Li, Weifeng (2015). "El problema del contexto geográfico incierto en la identificación de centros de actividad mediante datos de posicionamiento de teléfonos móviles y datos de puntos de interés". Avances en el manejo y análisis de datos espaciales . Avances en la ciencia de la información geográfica. págs. 107–119. doi :10.1007/978-3-319-19950-4_7. ISBN 978-3-319-19949-8.
25. Allen, Jeff (2019). "Uso de segmentos de red en la visualización de isócronas urbanas". Cartographica: La revista internacional de información geográfica y geovisualización . 53 (4): 262–270. doi :10.3138/cart.53.4.2018-0013. S2CID  133986477.
26. Zhao, Pengxiang; Kwan, Mei-Po; Zhou, Suhong (2018). "El problema del contexto geográfico incierto en el análisis de las relaciones entre la obesidad y el entorno construido en Guangzhou". Revista internacional de investigación ambiental y salud pública . 15 (2): 308. doi : 10.3390/ijerph15020308 . PMC 5858377 . PMID  29439392. 
27. Zhou, Xingang; Liu, Jianzheng; Yeh, Anthony Gar On; Yue, Yang; Li, Weifeng (2015). "El problema del contexto geográfico incierto en la identificación de centros de actividad mediante datos de posicionamiento de teléfonos móviles y datos de puntos de interés". Avances en el manejo y análisis de datos espaciales . Avances en la ciencia de la información geográfica. págs. 107–119. doi :10.1007/978-3-319-19950-4_7. ISBN 978-3-319-19949-8. Recuperado el 22 de enero de 2023 .
28. Tobler, Waldo (2004). "Sobre la primera ley de la geografía: una respuesta". Anales de la Asociación de Geógrafos Estadounidenses . 94 (2): 304–310. doi :10.1111/j.1467-8306.2004.09402009.x. S2CID  33201684 . Consultado el 10 de marzo de 2022 .
29. Salvo, Deborah; Durand, Casey P.; Dooley, Erin E.; Johnson, Ashleigh M.; Oluyomi, Abiodun; Gabriel, Kelley P.; Van Dan Berg, Alexandra; Perez, Adriana; Kohl, Harold W. (junio de 2019). "Reducción del problema del contexto geográfico incierto en la investigación sobre actividad física: el estudio TRAIN de Houston". Medicina y ciencia en deportes y ejercicio . 51 (6S): 437. doi :10.1249/01.mss.0000561808.49993.53. S2CID  198375226.
30. Thrift, Nigel (1977). Introducción a la geografía del tiempo (PDF) . Geo Abstracts, Universidad de East Anglia. ISBN 0-90224667-4.
31. Shmool, Jessie L.; Johnson, Isaac L.; Dodson, Zan M.; Keene, Robert; Gradeck, Robert; Beach, Scott R.; Clougherty, Jane E. (2018). "Desarrollo de un instrumento de encuesta en línea basado en SIG para obtener geografías de vecindarios percibidas para abordar el problema del contexto geográfico incierto". El geógrafo profesional . 70 (3): 423–433. Bibcode :2018ProfG..70..423S. doi :10.1080/00330124.2017.1416299. S2CID  135366460 . Consultado el 22 de enero de 2023 .
32. Journel, AG y Huijbregts, CJ, Geoestadística minera , Academic Press Inc, Londres.
33. von Csefalvay, Chris (2023), "Dinámica espacial de las epidemias", Modelado computacional de enfermedades infecciosas , Elsevier, págs. 257-303, doi :10.1016/b978-0-32-395389-4.00017-7, ISBN 978-0-323-95389-4, consultado el 5 de marzo de 2023
34. Knegt, De; Coughenour, MB; Skidmore, AK; Heitkönig, IMA; Knox, NM; Slotow, R.; Prins, HHT (2010). "Autocorrelación espacial y escalamiento de las relaciones entre especies y ambiente". Ecología . 91 (8): 2455–2465. Bibcode :2010Ecol...91.2455D. doi :10.1890/09-1359.1. PMID  20836467.
35. "Spatial Association" (PDF) . Asociación de profesores de geografía de Victoria . Consultado el 17 de noviembre de 2014 .
36. Song, Yongze (julio de 2022). "La segunda dimensión de la asociación espacial". Revista internacional de observación de la Tierra y geoinformación aplicadas . 111 : 102834. doi : 10.1016/j.jag.2022.102834 . hdl : 20.500.11937/88649 . S2CID  249166886.
37. Halley, JM; Hartley, S.; Kallimanis, AS; Kunin, WE; Lennon, JJ; Sgardelis, SP (1 de marzo de 2004). "Usos y abusos de la metodología fractal en ecología". Ecology Letters . 7 (3): 254–271. Bibcode :2004EcolL...7..254H. doi :10.1111/j.1461-0248.2004.00568.x. ISSN  1461-0248.
38. Ocaña-Riola, R (2010). "Errores comunes en el mapeo de enfermedades". Salud Geoespacial . 4 (2): 139–154. doi : 10.4081/gh.2010.196 . PMID  20503184.
39. "Entender las falacias espaciales". Guía del alumno para el análisis geoespacial . Departamento de Geografía de Penn State . Consultado el 27 de abril de 2018 .
40. Quattrochi, Dale A (1 de febrero de 2016). Integración de la escala en teledetección y SIG . Taylor & Francis. ISBN 9781482218268.OCLC 973767077  .
41. Robinson, Ws (abril de 2009). "Correlaciones ecológicas y el comportamiento de los individuos*". Revista Internacional de Epidemiología . 38 (2): 337–341. doi : 10.1093/ije/dyn357 . PMID  19179346.
42. Graham J. Upton y Bernard Fingelton: Análisis de datos espaciales mediante ejemplos Volumen 1: Patrones de puntos y datos cuantitativos John Wiley & Sons, Nueva York. 1985.
43. Harman HH (1960) Análisis factorial moderno , University of Chicago Press
44. Rummel RJ (1970) Análisis factorial aplicado . Evanston, ILL: Northwestern University Press.
45. Bell W & E Shevky (1955) Análisis del área social , Stanford University Press
46. Moser CA y W Scott (1961) Ciudades británicas: un estudio estadístico de sus diferencias sociales y económicas , Oliver y Boyd, Londres.
47. Berry BJ y F Horton (1971) Perspectivas geográficas sobre sistemas urbanos , John Wiley, NY.
48. Berry BJ y KB Smith eds (1972) Manual de clasificación de ciudades: métodos y aplicaciones , John Wiley, NY.
49. Ciceri MF (1974) Méthodes d'analyse multivariée dans la géographie anglo-saxonne , Université de Paris-1; descarga gratuita en http://www-ohp.univ-paris1.fr
50. Tucker LR (1964) « La extensión del análisis factorial a matrices tridimensionales », en Frederiksen N & H Gulliksen eds, Contribuciones a la psicología matemática , Holt, Rinehart y Winston, NY.
51. R. Coppi y S. Bolasco, eds. (1989), Análisis de datos multidireccionales , Elsevier, Amsterdam.
52. Cant, RG (1971). "Cambios en la localización de la manufactura en Nueva Zelanda 1957-1968: Una aplicación del análisis factorial de tres modos". New Zealand Geographer . 27 (1): 38–55. Bibcode :1971NZGeo..27...38C. doi :10.1111/j.1745-7939.1971.tb00636.x.
53. Marchand B (1986) El surgimiento de Los Ángeles, 1940-1970 , Pion Ltd, Londres
54. Brunsdon, C.; Fotheringham, AS; Charlton, ME (1996). "Regresión ponderada geográficamente: un método para explorar la no estacionariedad espacial". Análisis geográfico . 28 (4): 281–298. Código Bibliográfico :1996GeoAn..28..281B. doi : 10.1111/j.1538-4632.1996.tb00936.x .
55. Banerjee, Sudipto; Carlin, Bradley P.; Gelfand, Alan E. (2014), Modelado y análisis jerárquico de datos espaciales, segunda edición , Monografías sobre estadística y probabilidad aplicada (2.ª ed.), Chapman y Hall/CRC, ISBN 9781439819173
56. Bivand, Roger (20 de enero de 2021). «Vista de tareas de CRAN: análisis de datos espaciales» . Consultado el 21 de enero de 2021 .
57. Banerjee, Sudipto ; Gelfand, Alan E. ; Finley, Andrew O.; Sang, Huiyan (2008). "Modelos de procesos predictivos gaussianos para grandes conjuntos de datos espaciales". Revista de la Royal Statistical Society, Serie B . 70 (4): 825–848. doi :10.1111/j.1467-9868.2008.00663.x. PMC 2741335 . PMID  19750209. 
58. Datta, Abhirup; Banerjee, Sudipto; Finley, Andrew O.; Gelfand, Alan E. (2016). "Modelos de proceso gaussiano jerárquico de vecino más cercano para grandes conjuntos de datos geoestadísticos". Revista de la Asociación Estadounidense de Estadística . 111 (514): 800–812. arXiv : 1406.7343 . doi :10.1080/01621459.2015.1044091. PMC 5927603. PMID  29720777 . 
59. Morer I, Cardillo A, Díaz-Guilera A, Prignano L, Lozano S (2020). "Comparación de redes espaciales: un enfoque de talla única basado en la eficiencia". Physical Review . 101 (4): 042301. Bibcode :2020PhRvE.101d2301M. doi :10.1103/PhysRevE.101.042301. hdl : 2445/161417 . PMID  32422764. S2CID  49564277.
60. Gupta J, Molnar C, Xie Y, Knight J, Shekhar S (2021). "Redes neuronales profundas que tienen en cuenta la variabilidad espacial (SVANN): un enfoque general". ACM Transactions on Intelligent Systems and Technology . 12 (6): 1–21. doi :10.1145/3466688. S2CID  244786699.
61. Hagenauer J, Helbich M (2022). "Una red neuronal artificial ponderada geográficamente". Revista Internacional de Ciencias de la Información Geográfica . 36 (2): 215–235. Código Bibliográfico :2022IJGIS..36..215H. doi : 10.1080/13658816.2021.1871618 . S2CID  233883395.
62. Silva, EA; Clarke, KC (2002). "Calibración del modelo de crecimiento urbano SLEUTH para Lisboa y Oporto, Portugal". Computers, Environment and Urban Systems . 26 (6): 525–552. Bibcode :2002CEUS...26..525S. doi :10.1016/S0198-9715(01)00014-X.
63. Silva, EA (2003). "Complejidad, emergencia y modelos urbanos celulares: lecciones aprendidas de la aplicación de SLEUTH a dos áreas metropolitanas portuguesas". Estudios de Planificación Europea . 13 (1): 93–115. doi :10.1080/0965431042000312424. S2CID  197257.
64. Liu y Silva (2017). "Examen de la dinámica de la interacción entre el desarrollo de las industrias creativas y la estructura espacial urbana mediante modelos basados ​​en agentes: un estudio de caso de Nanjing, China". Estudios urbanos . 65 (5): 113–125. doi : 10.1177/0042098016686493 . S2CID  157318972.
65. Liu, Lun; Silva, Elisabete A.; Wu, Chunyang; Wang, Hui (2017). "Un método basado en el aprendizaje automático para la evaluación a gran escala de las cualidades del entorno urbano" (PDF) . Computers Environment and Urban Systems . 65 : 113–125. Bibcode :2017CEUS...65..113L. doi : 10.1016/j.compenvurbsys.2017.06.003 .
66. Honarkhah, M; Caers, J (2010). "Simulación estocástica de patrones utilizando modelado de patrones basado en la distancia". Geociencias matemáticas . 42 (5): 487–517. Código Bibliográfico :2010MaGeo..42..487H. doi :10.1007/s11004-010-9276-7. S2CID  73657847.
67. Tahmasebi, P.; Hezarkhani, A.; Sahimi, M. (2012). "Modelado geoestadístico de puntos múltiples basado en las funciones de correlación cruzada". Geociencias computacionales . 16 (3): 779–79742. Código Bibliográfico :2012CmpGe..16..779T. doi :10.1007/s10596-012-9287-1. S2CID  62710397.
68. Tahmasebi, P.; Sahimi, M. (2015). "Reconstrucción de materiales y medios desordenados no estacionarios: transformada de cuenca hidrográfica y función de correlación cruzada". Physical Review E . 91 (3): 032401. Bibcode :2015PhRvE..91c2401T. doi : 10.1103/PhysRevE.91.032401 . PMID  25871117.
69. Tahmasebi, P.; Sahimi, M. (2015). "Simulación geoestadística y reconstrucción de medios porosos mediante una función de correlación cruzada e integración de datos duros y blandos". Transporte en medios porosos . 107 (3): 871–905. Bibcode :2015TPMed.107..871T. doi :10.1007/s11242-015-0471-3. S2CID  123432975.
70. "Programa de posgrado en análisis espacial". Universidad Ryerson . Consultado el 17 de diciembre de 2015 .
71. geoespacial. Diccionario Collins de inglés, completo y sin abreviar, 11.ª edición. Consultado el 5 de agosto de 2012 en el sitio web CollinsDictionary.com: http://www.collinsdictionary.com/dictionary/english/geospatial
72. Léxico del siglo XXI de Dictionary.com Copyright © 2003-2010 Dictionary.com, LLC http://dictionary.reference.com/browse/geospatial
73. La red geoespacial: la fusión de espacios físicos y virtuales. Archivado el 2 de octubre de 2011 en Wayback Machine . Arno Scharl en la revista Receiver, otoño de 2008
74. Chen, Ruizhi; Guinness, Robert E. (2014). Computación geoespacial en dispositivos móviles (1.ª ed.). Norwood, MA: Artech House. pág. 228. ISBN 978-1-60807-565-2. Recuperado el 1 de julio de 2014 .
75. González, Ainhoa; Donnelly, Alison; Jones, Mike; Chrysoulakis, Nektarios; Lopes, Myriam (2012). "Un sistema de apoyo a la toma de decisiones para el metabolismo urbano sostenible en Europa". Environmental Impact Assessment Review . 38 : 109–119. doi :10.1016/j.eiar.2012.06.007.

Lectura adicional

• Abler, R., J. Adams y P. Gould (1971) Organización espacial: la visión del mundo del geógrafo , Englewood Cliffs, Nueva Jersey: Prentice-Hall.
• Anselin, L. (1995) "Indicadores locales de asociación espacial – LISA". Análisis geográfico, 27, 93–115.
• Awange, Joseph; Paláncz, Béla (2016). Cálculos algebraicos geoespaciales, teoría y aplicaciones, tercera edición . Nueva York: Springer. ISBN 978-3319254630.
• Banerjee, Sudipto; Carlin, Bradley P.; Gelfand, Alan E. (2014), Modelado y análisis jerárquico de datos espaciales, segunda edición , Monografías sobre estadística y probabilidad aplicada (2.ª ed.), Chapman y Hall/CRC, ISBN 9781439819173
• Benenson, I. y PM Torrens. (2004). Geosimulación: modelado de fenómenos urbanos basado en autómatas. Wiley.
• Fotheringham, AS, C. Brunsdon y M. Charlton (2000) Geografía cuantitativa: perspectivas sobre el análisis de datos espaciales , Sage.
• Fotheringham, AS y ME O'Kelly (1989) Modelos de interacción espacial: formulaciones y aplicaciones , Kluwer Academic
• Fotheringham, AS; Rogerson, PA (1993). "SIG y problemas analíticos espaciales". Revista Internacional de Sistemas de Información Geográfica . 7 : 3–19. doi :10.1080/02693799308901936.
• Goodchild, MF (1987). "Una perspectiva analítica espacial sobre los sistemas de información geográfica". Revista Internacional de Sistemas de Información Geográfica . 1 (4): 327–44. doi :10.1080/02693798708927820.
• MacEachren, AM y DRF Taylor (eds.) (1994) Visualización en cartografía moderna , Pergamon.
• Levine, N. (2010). CrimeStat: Un programa de estadísticas espaciales para el análisis de las ubicaciones de los incidentes delictivos . Versión 3.3. Ned Levine & Associates, Houston, TX y el Instituto Nacional de Justicia, Washington, DC. Cap. 1-17 + 2 capítulos de actualización
• Miller, HJ (2004). "La primera ley de Tobler y el análisis espacial". Anales de la Asociación de Geógrafos Estadounidenses . 94 (2): 284–289. doi :10.1111/j.1467-8306.2004.09402005.x. S2CID  19172678.
• Miller, HJ y J. Han (eds.) (2001) Minería de datos geográficos y descubrimiento de conocimiento , Taylor y Francis.
• O'Sullivan, D. y D. Unwin (2002) Análisis de información geográfica , Wiley.
• Parker, DC; Manson, SM; Janssen, MA ; Hoffmann, MJ; Deadman, P. (2003). "Sistemas multiagente para la simulación del cambio de uso y cobertura del suelo: una revisión". Anales de la Asociación de Geógrafos Estadounidenses . 93 (2): 314–337. CiteSeerX  10.1.1.109.1825 . doi :10.1111/1467-8306.9302004. S2CID  130096094.
• White, R.; Engelen, G. (1997). "Autómatas celulares como base del modelado regional dinámico integrado". Environment and Planning B: Planning and Design . 24 (2): 235–246. Bibcode :1997EnPlB..24..235W. doi :10.1068/b240235. S2CID  62516646.
• Scheldeman, X. y van Zonneveld, M. (2010). Manual de capacitación sobre análisis espacial de la diversidad y distribución de plantas. Bioversity International.
• Fisher MM, Leung Y (2001) Modelado geocomputacional: técnicas y aplicaciones. Springer Verlag, Berlín
• Fotheringham, S; Clarke, G; Abrahart, B (1997). "Geocomputación y SIG". Transactions in GIS . 2 (3): 199–200. doi :10.1111/j.1467-9671.1997.tb00010.x. S2CID  205576122.
• Openshaw S y Abrahart RJ (2000) GeoComputación. CRC Press
• Diappi Lidia (2004) Ciudades en evolución: geocomputación en la planificación territorial. Ashgate, Inglaterra
• Longley PA, Brooks SM, McDonnell R, Macmillan B (1998), Geocomputación, una introducción. John Wiley and Sons, Chichester
• Ehlen, J; Caldwell, DR; Harding, S (2002). "GeoComputación: ¿qué es?". Comput Environ and Urban Syst . 26 (4): 257–265. Bibcode :2002CEUS...26..257E. doi :10.1016/s0198-9715(01)00047-3.
• Gahegan, M (1999). "¿Qué es la geocomputación?". Transactions in GIS . 3 (3): 203–206. doi :10.1111/1467-9671.00017. S2CID  44656909.
• Murgante B., Borruso G., Lapucci A. (2009) "Geocomputación y planificación urbana" Estudios en Inteligencia Computacional , Vol. 176. Springer-Verlag, Berlín.
• Reis, José P.; Silva, Elisabete A.; Pinho, Paulo (2016). "Métricas espaciales para estudiar patrones urbanos en ciudades en crecimiento y en contracción". Geografía urbana . 37 (2): 246–271. doi :10.1080/02723638.2015.1096118. S2CID  62886095.
• Papadimitriou, F. (2002). "Modelización de indicadores e índices de complejidad del paisaje: un enfoque que utiliza SIG". Indicadores ecológicos . 2 (1–2): 17–25. Bibcode :2002EcInd...2...17P. doi :10.1016/S1470-160X(02)00052-3.
• Fischer M., Leung Y. (2010) "Modelado geocomputacional: técnicas y aplicaciones" Avances en la ciencia espacial. Springer-Verlag, Berlín.
• Murgante B., Borruso G., Lapucci A. (2011) "Geocomputación, sostenibilidad y planificación ambiental" Estudios en Inteligencia Computacional , Vol. 348. Springer-Verlag, Berlín.
• Tahmasebi, P.; Hezarkhani, A.; Sahimi, M. (2012). "Modelado geoestadístico de puntos múltiples basado en las funciones de correlación cruzada". Geociencias Computacionales . 16 (3): 779–79742. Bibcode :2012CmpGe..16..779T. doi :10.1007/s10596-012-9287-1. S2CID  62710397.
• Geza, Tóth; Áron, Kincses; Zoltán, Nagy (2014). Estructura espacial europea . Publicaciones académicas LAP LAMBERT. doi :10.13140/2.1.1560.2247.

Enlaces externos

• Comisión de Análisis y Modelado Geoespacial de la ACI
• Un recurso educativo sobre estadística espacial y geoestadística
• Una guía completa de principios, técnicas y herramientas de software.
• Desigualdades sociales y espaciales
• Centro Nacional de Información y Análisis Geográfico (NCGIA)
• Asociación Cartográfica Internacional (ACI): el organismo mundial para profesionales de la cartografía y la ciencia SIG