Singularidad BKL

General relativity model near the beginning of the universe

Un cuerpo esférico que experimenta una dinámica BKL (Mixmaster) caótica cercana a la singularidad según las reglas de la ecuación 35. La simulación se realizó en Mathematica con . inicial . ^{[nota 1]} ${\displaystyle u={\sqrt {13}}}$

Una singularidad de Belinski–Khalatnikov–Lifshitz (BKL) es un modelo de la evolución dinámica del universo cerca de la singularidad gravitacional inicial , descrita por una solución anisotrópica y caótica de la ecuación de campo de la gravitación de Einstein . ^[2] Según este modelo, el universo oscila caóticamente alrededor de una singularidad gravitacional en la que el tiempo y el espacio se vuelven iguales a cero o, equivalentemente, la curvatura del espacio-tiempo se vuelve infinitamente grande. Esta singularidad es físicamente real en el sentido de que es una propiedad necesaria de la solución, y aparecerá también en la solución exacta de esas ecuaciones. La singularidad no se crea artificialmente por las suposiciones y simplificaciones realizadas por las otras soluciones especiales como las soluciones de Friedmann–Lemaître–Robertson–Walker , cuasi-isotrópica y de Kasner .

El modelo lleva el nombre de sus autores Vladimir Belinski , Isaak Khalatnikov y Evgeny Lifshitz , que entonces trabajaban en el Instituto Landau de Física Teórica .

La imagen desarrollada por BKL tiene varios elementos importantes. Estos son:

• Cerca de la singularidad, la evolución de la geometría en diferentes puntos espaciales se desacopla de modo que las soluciones de las ecuaciones diferenciales parciales pueden aproximarse mediante soluciones de ecuaciones diferenciales ordinarias con respecto al tiempo para factores de escala espacial definidos adecuadamente. Esto se denomina conjetura BKL .
• Para la mayoría de los tipos de materia, el efecto de los campos de materia sobre la dinámica de la geometría se vuelve insignificante cerca de la singularidad. O, en palabras de John Wheeler , "la materia no importa" cerca de una singularidad. El trabajo original de BKL planteó un efecto insignificante para toda la materia, pero más tarde teorizaron que la "materia rígida" (ecuación de estado p = ε) equivalente a un campo escalar sin masa puede tener un efecto modificador sobre la dinámica cerca de la singularidad.
• Las ecuaciones diferenciales ordinarias que describen las asintóticas provienen de una clase de soluciones espacialmente homogéneas que constituyen la dinámica Mixmaster : un modelo oscilatorio y caótico complicado que exhibe propiedades similares a las discutidas por BKL.

El estudio de la dinámica del universo en las proximidades de la singularidad cosmológica se ha convertido en un campo de rápido desarrollo de la física teórica y matemática moderna. La generalización del modelo BKL a la singularidad cosmológica en modelos cosmológicos multidimensionales ( tipo Kaluza-Klein ) tiene un carácter caótico en los espacio-tiempos cuya dimensionalidad no es superior a diez, mientras que en los espacio-tiempos de dimensionalidades superiores un universo después de sufrir un número finito de oscilaciones entra en un régimen de contracción monótono de tipo Kasner. ^{[3] [4] [5]}

El desarrollo de los estudios cosmológicos basados ​​en modelos de supercuerdas ha revelado algunos aspectos nuevos de la dinámica en la vecindad de la singularidad. ^{[6] [7] [8]} En estos modelos, los mecanismos de cambio de las épocas de Kasner no son provocados por las interacciones gravitacionales sino por la influencia de otros campos presentes. Se demostró que los modelos cosmológicos basados ​​en seis modelos principales de supercuerdas más un modelo de supergravedad de once dimensiones exhiben la dinámica caótica de BKL hacia la singularidad. Se descubrió una conexión entre los modelos cosmológicos oscilatorios similares a BKL y una subclase especial de álgebras de Lie de dimensión infinita : las llamadas álgebras hiperbólicas de Kac-Moody . ^{[9] [10] [11]}

Introducción

La base de la cosmología moderna son las soluciones especiales de las ecuaciones de campo de Einstein encontradas por Alexander Friedmann en 1922-1924. El Universo se supone homogéneo (el espacio tiene las mismas propiedades métricas (medidas) en todos los puntos) e isótropo (el espacio tiene las mismas medidas en todas las direcciones). Las soluciones de Friedmann permiten dos posibles geometrías para el espacio: modelo cerrado con un espacio en forma de bola, arqueado hacia afuera ( curvatura positiva ) y modelo abierto con un espacio en forma de silla de montar, arqueado hacia adentro ( curvatura negativa ). En ambos modelos, el Universo no está quieto, está constantemente expandiéndose (haciéndose más grande) o contrayéndose (encogiéndose, haciéndose más pequeño). Esto fue confirmado por Edwin Hubble quien estableció el corrimiento al rojo de Hubble de las galaxias en retroceso. El consenso actual es que el modelo isótropo , en general, da una descripción adecuada del estado actual del Universo; sin embargo, la isotropía del Universo actual por sí misma no es una razón para esperar que sea adecuado para describir las primeras etapas de la evolución del Universo . Al mismo tiempo, es obvio que en el mundo real la homogeneidad es, en el mejor de los casos, sólo una aproximación. Incluso si se puede hablar de una distribución homogénea de la densidad de materia a distancias grandes en comparación con el espacio intergaláctico, esta homogeneidad desaparece a escalas más pequeñas. Por otro lado, el supuesto de homogeneidad va muy lejos en un aspecto matemático: hace que la solución sea altamente simétrica , lo que puede impartir propiedades específicas que desaparecen cuando se considera un caso más general.

Otra propiedad importante del modelo isótropo es la existencia inevitable de una singularidad temporal : el flujo del tiempo no es continuo, sino que se detiene o se invierte después de que el tiempo alcanza un valor muy grande o muy pequeño. Entre singularidades, el tiempo fluye en una dirección: alejándose de la singularidad ( flecha del tiempo ). En el modelo abierto, hay una singularidad temporal, por lo que el tiempo está limitado en un extremo pero ilimitado en el otro, mientras que en el modelo cerrado hay dos singularidades que limitan el tiempo en ambos extremos (el Big Bang y el Big Crunch ).

Las únicas propiedades físicamente interesantes de los espacio-tiempos (como las singularidades) son aquellas que son estables , es decir, aquellas propiedades que todavía ocurren cuando los datos iniciales son perturbados ligeramente. Es posible que una singularidad sea estable y, sin embargo, no tenga interés físico: la estabilidad es una condición necesaria pero no suficiente para la relevancia física. Por ejemplo, una singularidad podría ser estable solo en un vecindario de conjuntos de datos iniciales correspondientes a universos altamente anisotrópicos . Dado que el universo real es ahora aparentemente casi isotrópico, una singularidad de este tipo no podría ocurrir en nuestro universo. Una condición suficiente para que una singularidad estable sea de interés físico es el requisito de que la singularidad sea genérica (o general). En términos generales, una singularidad estable es genérica si ocurre cerca de cada conjunto de condiciones iniciales y los campos no gravitacionales están restringidos de alguna manera específica a campos "físicamente realistas" de modo que se supone que las ecuaciones de Einstein, varias ecuaciones de estado, etc., se mantienen en los espacio-tiempos evolucionados. Podría suceder que una singularidad sea estable bajo pequeñas variaciones de los verdaderos grados de libertad gravitacionales , y sin embargo no sea genérica porque la singularidad depende de alguna manera del sistema de coordenadas , o más bien de la elección de la hipersuperficie inicial a partir de la cual se desarrolla el espacio-tiempo.

Para un sistema de ecuaciones diferenciales no lineales , como las ecuaciones de Einstein , una solución general no está definida de forma inequívoca. En principio, puede haber múltiples integrales generales , y cada una de ellas puede contener solo un subconjunto finito de todas las condiciones iniciales posibles . Cada una de esas integrales puede contener todas las funciones independientes requeridas que, sin embargo, pueden estar sujetas a algunas condiciones (por ejemplo, algunas desigualdades ). La existencia de una solución general con una singularidad, por lo tanto, no excluye la existencia de otras soluciones generales adicionales que no contengan una singularidad. Por ejemplo, no hay razón para dudar de la existencia de una solución general sin una singularidad que describa un cuerpo aislado con una masa relativamente pequeña.

Es imposible encontrar una integral general para todo el espacio y para todo el tiempo. Sin embargo, esto no es necesario para resolver el problema: basta con estudiar la solución cerca de la singularidad. Esto resolvería también otro aspecto del problema: las características de la evolución de la métrica del espacio-tiempo en la solución general cuando alcanza la singularidad física, entendida como un punto donde la densidad de materia y los invariantes del tensor de curvatura de Riemann se hacen infinitos.

Existencia de la singularidad del tiempo físico

Uno de los principales problemas estudiados por el grupo de Landau (al que pertenece BKL) fue si los modelos cosmológicos relativistas contienen necesariamente una singularidad temporal o si la singularidad temporal es un artefacto de los supuestos utilizados para simplificar estos modelos. La independencia de la singularidad con respecto a los supuestos de simetría significaría que las singularidades temporales existen no sólo en las soluciones especiales, sino también en las generales de las ecuaciones de Einstein. Es razonable sugerir que si una singularidad está presente en la solución general, debe haber algunas indicaciones que se basan sólo en las propiedades más generales de las ecuaciones de Einstein, aunque esas indicaciones por sí mismas podrían ser insuficientes para caracterizar la singularidad.

Un criterio de generalidad de las soluciones es el número de funciones de coordenadas espaciales independientes que contienen. Estas incluyen sólo las funciones "físicamente independientes" cuyo número no puede reducirse mediante la elección de ningún sistema de referencia . En la solución general, el número de tales funciones debe ser suficiente para definir completamente las condiciones iniciales (distribución y movimiento de materia, distribución del campo gravitatorio ) en algún momento del tiempo elegido como inicial. Este número es cuatro para un espacio vacío (vacío), y ocho para un espacio lleno de materia y/o radiación. ^{[12] [13]}

Trabajos previos del grupo de Landau; ^{[14] [15] [16]} revisados ​​en ^[12] ) llevaron a la conclusión de que la solución general no contiene una singularidad física. Esta búsqueda de una clase más amplia de soluciones con una singularidad se ha hecho, esencialmente, mediante un método de ensayo y error, ya que faltaba un enfoque sistemático para el estudio de las ecuaciones de Einstein. Un resultado negativo, obtenido de esta manera, no es convincente por sí mismo; una solución con el grado necesario de generalidad lo invalidaría, y al mismo tiempo confirmaría cualquier resultado positivo relacionado con la solución específica.

En ese momento, la única indicación conocida de la existencia de singularidad física en la solución general estaba relacionada con la forma de las ecuaciones de Einstein escritas en un marco sincrónico , es decir, en un marco en el que el tiempo propio x ⁰ = t está sincronizado en todo el espacio; en este marco el elemento de distancia espacial dl está separado del intervalo de tiempo dt . ^{[nota 2]} La ecuación de Einstein

escrito en un marco sincrónico da un resultado en el que el determinante métrico g inevitablemente se vuelve cero en un tiempo finito independientemente de cualquier suposición sobre la distribución de la materia. ^{[12] [13]}

Sin embargo, los esfuerzos por encontrar una singularidad física general se abandonaron cuando se hizo evidente que la singularidad mencionada anteriormente está vinculada con una propiedad geométrica específica del marco sincrónico: el cruce de coordenadas de la línea de tiempo. Este cruce tiene lugar en algunas hipersuperficies circundantes que son análogas cuatridimensionales de las superficies cáusticas en óptica geométrica ; g se vuelve cero exactamente en este cruce. ^[16] Por lo tanto, aunque esta singularidad es general, es ficticia y no física; desaparece cuando se cambia el marco de referencia. Esto, aparentemente, disuadió a los investigadores de realizar más investigaciones en esta línea.

Pasaron varios años hasta que el interés por este problema volvió a aumentar cuando Penrose  (1965) publicó sus teoremas que vinculaban la existencia de una singularidad de carácter desconocido con algunos supuestos muy generales que no tenían nada en común con la elección de un sistema de referencia. Otros teoremas similares fueron descubiertos más tarde por Hawking ^{[17] [18]} y Geroch ^[19] (véase Teoremas de singularidad de Penrose-Hawking ). Esto reavivó el interés por la búsqueda de soluciones singulares.

Solución homogénea generalizada

En un espacio que es a la vez homogéneo e isótropo, la métrica está completamente determinada, dejando libre únicamente el signo de la curvatura. Suponiendo que solo hay homogeneidad espacial sin ninguna simetría adicional, como la isotropía, se deja considerablemente más libertad para elegir la métrica. Lo siguiente se refiere a la parte espacial de la métrica en un instante dado de tiempo t, suponiendo un marco sincrónico de modo que t sea el mismo tiempo sincronizado para todo el espacio.

La conjetura de BKL

En su trabajo de 1970, ^[2] BKL afirmó que a medida que uno se acerca a una singularidad, los términos que contienen derivadas temporales en las ecuaciones de Einstein dominan sobre aquellos que contienen derivadas espaciales . Esto se conoce desde entonces como la conjetura de BKL e implica que las ecuaciones diferenciales parciales (EDP) de Einstein se aproximan bien mediante ecuaciones diferenciales ordinarias (EDO), por lo que la dinámica de la relatividad general se vuelve efectivamente local y oscilatoria. La evolución temporal de los campos en cada punto espacial se aproxima bien mediante las cosmologías homogéneas en la clasificación de Bianchi.

Separando las derivadas temporales y espaciales en las ecuaciones de Einstein, por ejemplo, de la manera utilizada para la clasificación de espacios homogéneos , y luego fijando los términos que contienen derivadas espaciales iguales a cero, se puede definir la llamada teoría truncada del sistema (ecuaciones truncadas). ^[20] Luego, la conjetura de BKL se puede hacer más específica:

Conjetura débil : A medida que se acerca la singularidad, los términos que contienen derivadas espaciales en las ecuaciones de Einstein son despreciables en comparación con los términos que contienen derivadas temporales. Por lo tanto, a medida que se acerca la singularidad, las ecuaciones de Einstein se aproximan a las que se encuentran al establecer los términos derivados en cero. Por lo tanto, la conjetura débil dice que las ecuaciones de Einstein pueden aproximarse bien mediante las ecuaciones truncadas en la vecindad de la singularidad. Obsérvese que esto no implica que las soluciones de las ecuaciones completas de movimiento se aproximen a las soluciones de las ecuaciones truncadas a medida que se acerca la singularidad. Esta condición adicional se captura en la versión fuerte de la siguiente manera.

Conjetura fuerte : A medida que se aproxima la singularidad, las ecuaciones de Einstein se aproximan a las de la teoría truncada y, además, las soluciones de las ecuaciones completas se aproximan bien a las soluciones de las ecuaciones truncadas.

Al principio, la conjetura de BKL parecía dependiente de las coordenadas y bastante improbable. Barrow y Tipler, ^{[21] [22]} por ejemplo, entre las diez críticas a los estudios de BKL, incluyen la elección inapropiada (según ellos) del marco sincrónico como medio para separar las derivadas temporales y espaciales. La conjetura de BKL a veces fue reformulada en la literatura como una afirmación de que cerca de la singularidad solo las derivadas temporales son importantes. Tal afirmación, tomada al pie de la letra, es errónea o, en el mejor de los casos, engañosa ya que, como se muestra en el propio análisis de BKL, los gradientes espaciales del tensor métrico no pueden descuidarse para soluciones genéricas de la gravedad de Einstein pura en cuatro dimensiones espaciotemporales y, de hecho, juegan un papel crucial en la aparición del régimen oscilatorio. Sin embargo, existen reformulaciones de la teoría de Einstein en términos de nuevas variables que involucran los gradientes relevantes, por ejemplo en variables de tipo Ashtekar, para las cuales la afirmación sobre el papel dominante de las derivadas temporales es correcta. ^[20] Es cierto que en cada punto espacial se obtiene una descripción efectiva de la singularidad en términos de un sistema dinámico de dimensión finita descrito por ecuaciones diferenciales ordinarias con respecto al tiempo, pero los gradientes espaciales entran en estas ecuaciones de manera no trivial.

Análisis posteriores realizados por un gran número de autores han demostrado que la conjetura BKL puede hacerse precisa y, a día de hoy, existe un impresionante conjunto de pruebas numéricas y analíticas que la respaldan. ^[23] Es justo decir que todavía estamos bastante lejos de una prueba de la conjetura fuerte. Pero ha habido un progreso sobresaliente en modelos más simples. En particular, Berger, Garfinkle, Moncrief, Isenberg, Weaver y otros demostraron que, en una clase de modelos, a medida que se aproxima la singularidad, las soluciones de las ecuaciones de campo de Einstein completas se aproximan a las "dominadas por el término de velocidad" (truncadas) obtenidas al descuidar las derivadas espaciales. ^{[23] [24] [25] [26] [27]} Andersson y Rendall ^[28] demostraron que para la gravedad acoplada a un campo escalar sin masa o un fluido rígido, para cada solución a las ecuaciones truncadas existe una solución a las ecuaciones de campo completo que converge a la solución truncada a medida que se aproxima a la singularidad, incluso en ausencia de simetrías. Estos resultados se generalizaron para incluir también campos de calibración de forma p . ^[29] En estos modelos truncados la dinámica es más simple, lo que permite una declaración precisa de la conjetura que podría probarse. En el caso general, la evidencia más sólida hasta la fecha proviene de evoluciones numéricas. Berger y Moncrief ^[30] comenzaron un programa para analizar singularidades cosmológicas genéricas. Mientras que el trabajo inicial se centró en casos de simetría reducida, ^[31] más recientemente Garfinkle ^[32] realizó una evolución numérica de espacio-tiempos sin simetrías en la que, de nuevo, el comportamiento mixmaster es evidente. Finalmente, un estudio numérico del comportamiento de los campos de prueba cerca de la singularidad de un agujero negro de Schwarzschild ha proporcionado apoyo adicional a la conjetura. ^[33]

Solución de Kasner

Dinámica de las métricas de Kasner, ecuación 2, en coordenadas esféricas hacia la singularidad. El parámetro de Lifshitz-Khalatnikov es u = 2 (1/ u = 0,5) y la coordenada r es 2 p _α (1/ u )τ donde τ es el tiempo logarítmico: τ = ln t . ^{[nota 3]} La contracción a lo largo de los ejes es lineal y anisotrópica (sin caoticidad).

El enfoque BKL para espacios homogéneos anisotrópicos (en oposición a isótropos) comienza con una generalización de una solución particular exacta derivada por Kasner ^[34] para un campo en el vacío, en el que el espacio es homogéneo y tiene una métrica euclidiana que depende del tiempo según la métrica de Kasner.

( dl es el elemento de línea ; dx , dy , dz son desplazamientos infinitesimales en las tres dimensiones espaciales y t es el período de tiempo transcurrido desde un momento inicial t ₀ = 0). Aquí, p ₁ , p ₂ , p ₃ son tres números cualesquiera que satisfagan las siguientes condiciones de Kasner

Debido a estas relaciones, sólo uno de los tres números es independiente (dos ecuaciones con tres incógnitas ). Los tres números nunca son iguales; dos números son iguales sólo en los conjuntos de valores y (0, 0, 1). ^{[nota 4]} En todos los demás casos los números son diferentes, un número es negativo y los otros dos son positivos. Esto se demuestra parcialmente elevando al cuadrado ambos lados de la primera condición de la ecuación 3 y desarrollando el cuadrado: ${\textstyle (-{\frac {1}{3}},{\frac {2}{3}},{\frac {2}{3}})}$

${\displaystyle \left(p_{1}+p_{2}+p_{3}\right)^{2}=\left(p_{1}^{2}+p_{2}^{2}+p_{3}^{2}\right)+\left(2p_{1}p_{2}+2p_{2}p_{3}+2p_{1}p_{3}\right)=1}$

El término es igual a 1 en virtud de la segunda condición de la ecuación 3 y, por lo tanto, el término con los productos mixtos debe ser cero. Esto es posible si al menos uno de los p ₁ , p ₂ , p ₃ es negativo. ${\displaystyle \left(p_{1}^{2}+p_{2}^{2}+p_{3}^{2}\right)}$

Si los números se ordenan en orden creciente, p ₁ < p ₂ < p ₃ , cambian en los intervalos (Fig. 4)

Gráfica de p ₁ , p ₂ , p ₃ con un argumento 1/ u . Los números p ₁ ( u ) y p ₃ ( u ) son monótonamente crecientes mientras que p ₂ ( u ) es una función monótonamente decreciente de u .

La métrica de Kasner (ecuación 2) corresponde a un espacio plano homogéneo pero anisotrópico en el que todos los volúmenes aumentan con el tiempo de tal manera que las distancias lineales a lo largo de dos ejes y y z aumentan mientras que la distancia a lo largo del eje x disminuye. El momento t = 0 causa una singularidad en la solución; la singularidad en la métrica en t = 0 no puede evitarse mediante ninguna transformación del marco de referencia. En la singularidad, los invariantes del tensor de curvatura de cuatro dimensiones tienden al infinito. Una excepción es el caso p ₁ = р ₂ = 0, р ₃ = 1; estos valores corresponden a un espaciotiempo plano: la transformación t sh z = ζ, t ch z = τ convierte la métrica de Kasner ( ecuación 2 ) en galileana .

BKL parametriza los números p ₁ , p ₂ , p _{3 en términos de un único} parámetro independiente (real) u (parámetro de Lifshitz-Khalatnikov ^[35] ) de la siguiente manera

La parametrización del índice de Kasner parece misteriosa hasta que se piensa en las dos restricciones de los índices eq. 3 . Ambas restricciones fijan la escala general de los índices de modo que sólo sus proporciones pueden variar. Es natural elegir una de esas proporciones como un nuevo parámetro, lo que se puede hacer de seis maneras diferentes. Eligiendo u = u ₃₂ = p ₃ / p ₂ , por ejemplo, es trivial expresar las seis proporciones posibles en términos de él. Eliminando p ₃ = up ₂ primero, y luego usando la restricción lineal para eliminar p ₁ = 1 − p ₂ − up ₂ = 1 − (1 + u ) p ₂ , la restricción cuadrática se reduce a una ecuación cuadrática en p ₂

con raíces p ₂ = 0 (obvio) y p ₂ = (1 + u ) / (1 + u + u ² ), de donde p ₁ y p ₃ se obtienen por sustitución hacia atrás . Se pueden definir seis parámetros de este tipo u _ab = p _a / p _b , para los cuales p _c ≤ p _b ≤ p _a cuando ( c , b , a ) es una permutación cíclica de (1, 2, 3). ^[36]

Todos los diferentes valores de p ₁ , p ₂ , p ₃ ordenados como se indica arriba se obtienen con u dentro del rango u ≥ 1. Los valores u < 1 se llevan a este rango de acuerdo con

En la solución generalizada, la forma correspondiente a la ecuación 2 se aplica sólo a la métrica asintótica (la métrica cercana a la singularidad t = 0), respectivamente, a los términos mayores de su desarrollo en serie por potencias de t . En el sistema de referencia sincrónico se escribe en la forma de la ecuación 1 con un elemento de distancia espacial

dónde

Los vectores tridimensionales l , m , n definen las direcciones en las que la distancia espacial cambia con el tiempo mediante las leyes de potencia de la ecuación 8 . Estos vectores, así como los números p _l , p _m , p _n que, como antes, están relacionados por la ecuación 3 , son funciones de las coordenadas espaciales. Las potencias p _l , p _m , p _n no están ordenadas en orden creciente, reservándose los símbolos p ₁ , p ₂ , p ₃ para los números de la ecuación 5 que permanecen ordenados en orden creciente. El determinante de la métrica de la ecuación 7 es

donde v = l [ mn ]. Es conveniente introducir las siguientes magnitudes ^{[nota 5]}

La métrica espacial en la ecuación 7 es anisotrópica porque las potencias de t en la ecuación 8 no pueden tener los mismos valores. Al acercarse a la singularidad en t = 0, las distancias lineales en cada elemento espacial disminuyen en dos direcciones y aumentan en la tercera dirección. El volumen del elemento disminuye en proporción a t .

La métrica de Kasner se introduce en las ecuaciones de Einstein sustituyendo el tensor métrico respectivo γ _αβ de la ecuación 7 sin definir a priori la dependencia de a , b , c de t : ^{[nota 2]}

${\displaystyle \varkappa _{\alpha }^{\beta }={\frac {2{\dot {a}}}{a}}l_{\alpha }l^{\beta }+{\frac {2{\dot {b}}}{b}}m_{\alpha }m^{\beta }+{\frac {2{\dot {c}}}{c}}n_{\alpha }n^{\beta }}$

donde el punto sobre un símbolo designa la diferenciación con respecto al tiempo. La ecuación de Einstein , ecuación 11, toma la forma

Todos sus términos son de segundo orden para la gran cantidad 1/ t (en t → 0) . En las ecuaciones de Einstein , ecuación 12 , los términos de dicho orden aparecen solo a partir de términos que están diferenciados en el tiempo. Si los componentes de P _αβ no incluyen términos de orden superior a dos, entonces

donde los índices l , m , n designan componentes tensoriales en las direcciones l , m , n . ^[12] Estas ecuaciones junto con la ecuación 14 dan las expresiones ecuación 8 con potencias que satisfacen la ecuación 3 .

Sin embargo, la presencia de una potencia negativa entre las 3 potencias p _l , p _m , p _n da como resultado la aparición de términos de P _αβ con un orden mayor que t ⁻² . Si la potencia negativa es p _l ( p _l = p ₁ < 0), entonces P _αβ contiene la función de coordenadas λ y la ecuación 12 se convierte en

Aquí, los segundos términos son de orden t ^{−2( p _m + p _n − p _l )} donde p _m + p _n − p _l = 1 + 2 | p _l | > 1. ^{[nota 6] Para eliminar estos términos y restaurar la} ecuación métrica 7 , es necesario imponer a las funciones de coordenadas la condición λ = 0.

Las tres ecuaciones de Einstein restantes (ecuación 13) contienen únicamente derivadas temporales de primer orden del tensor métrico. Proporcionan tres relaciones independientes del tiempo que deben imponerse como condiciones necesarias a las funciones de coordenadas en la ecuación 7. Esto, junto con la condición λ = 0, da lugar a cuatro condiciones. Estas condiciones vinculan diez funciones de coordenadas diferentes: tres componentes de cada uno de los vectores l , m , n y una función en las potencias de t (cualquiera de las funciones p _l , p _m , p _n , que están vinculadas por las condiciones de la ecuación 3 ). Al calcular el número de funciones físicamente arbitrarias, debe tenerse en cuenta que el sistema sincrónico utilizado aquí permite transformaciones arbitrarias independientes del tiempo de las tres coordenadas espaciales. Por lo tanto, la solución final contiene en total 10 − 4 − 3 = 3 funciones físicamente arbitrarias, que es una menos de lo que se necesita para la solución general en el vacío.

El grado de generalidad alcanzado en este punto no se reduce con la introducción de la materia; la materia se escribe en la ecuación métrica 7 y aporta cuatro nuevas funciones de coordenadas necesarias para describir la distribución inicial de su densidad y los tres componentes de su velocidad. Esto hace posible determinar la evolución de la materia simplemente a partir de las leyes de su movimiento en un campo gravitatorio dado a priori, que son las ecuaciones hidrodinámicas .

donde u ⁱ es la velocidad de 4 dimensiones, ε y σ son las densidades de energía y entropía de la materia (cf. ^[37] y; ^[38] también; ^[39] para detalles véase ^[40] ). Para la ecuación de estado ultrarrelativista p = ε/3 la entropía σ ~ ε ^1/4 . Los términos principales en la ecuación 17 y la ecuación 18 son aquellos que contienen derivadas temporales . A partir de la ecuación 17 y los componentes espaciales de la ecuación 18 se tiene

${\displaystyle {\frac {\partial }{\partial t}}\left({\sqrt {-g}}u_{0}\varepsilon ^{\frac {3}{4}}\right)=0,\ 4\varepsilon \cdot {\frac {\partial u_{\alpha }}{\partial t}}+u_{\alpha }\cdot {\frac {\partial \varepsilon }{\partial t}}=0,}$

Resultando en

donde 'const' son cantidades independientes del tiempo. Además, a partir de la identidad u _i u ⁱ = 1 se tiene (porque todos los componentes covariantes de u _α son del mismo orden)

${\displaystyle u_{0}^{2}\approx u_{n}u^{n}={\frac {u_{n}^{2}}{c^{2}}},}$

donde u _n es el componente de velocidad a lo largo de la dirección de n que está conectado con la potencia más alta (positiva) de t (suponiendo que p _n = p ₃ ). De las relaciones anteriores, se deduce que

o

Las ecuaciones anteriores se pueden utilizar para confirmar que los componentes del tensor de tensión-energía-momento de la materia que se encuentran en el lado derecho de las ecuaciones

${\displaystyle R_{0}^{0}=T_{0}^{0}-{\frac {1}{2}}T,\ R_{\alpha }^{\beta }=T_{\alpha }^{\beta }-{\frac {1}{2}}\delta _{\alpha }^{\beta }T,}$

son, de hecho, de un orden inferior en 1/ t a los términos mayores en sus lados izquierdos. En las ecuaciones, la presencia de materia resulta únicamente en el cambio de relaciones impuestas sobre sus funciones de coordenadas constituyentes. ^[12] ${\displaystyle R_{\alpha }^{0}=T_{\alpha }^{0}}$

El hecho de que ε se vuelva infinito por la ley de la ecuación 21 confirma que en la solución de la ecuación 7 se trata de una singularidad física para cualquier valor de las potencias p ₁ , p ₂ , p ₃ exceptuando únicamente (0, 0, 1). Para estos últimos valores, la singularidad no es física y puede eliminarse mediante un cambio de sistema de referencia.

La singularidad ficticia correspondiente a las potencias (0, 0, 1) surge como resultado de que las coordenadas de la línea de tiempo se crucen sobre una " superficie focal " bidimensional. Como se señala en ^[12] , siempre se puede elegir un marco de referencia sincrónico de tal manera que este inevitable cruce de la línea de tiempo ocurra exactamente sobre dicha superficie (en lugar de una superficie cáustica tridimensional). Por lo tanto, debe existir una solución con tal singularidad ficticia simultánea para todo el espacio con un conjunto completo de funciones arbitrarias necesarias para la solución general. Cerca del punto t = 0 permite una expansión regular por potencias enteras de t . Para un análisis de este caso, véase ^{[41] .}

Modo oscilante hacia la singularidad

La solución general es, por definición, completamente estable; de ​​lo contrario, el Universo no existiría. Cualquier perturbación equivale a un cambio en las condiciones iniciales en un momento dado; como la solución general permite condiciones iniciales arbitrarias, la perturbación no es capaz de cambiar su carácter. Vistas desde este ángulo, las cuatro condiciones impuestas a las funciones de coordenadas en la solución de la ecuación 7 son de tipos diferentes: tres condiciones que surgen de las ecuaciones = 0 son "naturales"; son una consecuencia de la estructura de las ecuaciones de Einstein. Sin embargo, la condición adicional λ = 0 que causa la pérdida de una función derivada, es de un tipo completamente diferente: la inestabilidad causada por perturbaciones puede romper esta condición. La acción de tal perturbación debe llevar al modelo a otro modo, más general. La perturbación no puede considerarse pequeña: una transición a un nuevo modo excede el rango de perturbaciones muy pequeñas. ${\displaystyle R_{\alpha }^{0}}$

El análisis del comportamiento del modelo bajo acción perturbativa, realizado por BKL, delinea un modo oscilatorio complejo al acercarse a la singularidad. ^{[2] [42] [43] [44]} No pudieron dar todos los detalles de este modo en el marco amplio del caso general. Sin embargo, BKL explicó las propiedades y el carácter más importantes de la solución en modelos específicos que permiten un estudio analítico de largo alcance.

Estos modelos se basan en una métrica espacial homogénea de un tipo particular. Suponer una homogeneidad del espacio sin ninguna simetría adicional deja una gran libertad en la elección de la métrica. Todos los espacios homogéneos (pero anisotrópicos) posibles se clasifican, según Bianchi , en varios tipos Bianchi (Tipo I a IX) . ^[45] (véase también Solución homogénea generalizada) BKL investiga solo espacios de los tipos Bianchi VIII y IX.

Si la métrica tiene la forma de la ecuación 7 , para cada tipo de espacios homogéneos existe alguna relación funcional entre los vectores de referencia l , m , n y las coordenadas espaciales. La forma específica de esta relación no es importante. El hecho importante es que para los espacios de Tipo VIII y IX, las cantidades λ, μ, ν ecuación 10 son constantes mientras que todos los productos "mixtos" l rot m , l rot n , m rot l , etc. son ceros. Para los espacios de Tipo IX, las cantidades λ, μ, ν tienen el mismo signo y se puede escribir λ = μ = ν = 1 (el cambio simultáneo de signo de las 3 constantes no cambia nada). Para los espacios de Tipo VIII, 2 constantes tienen un signo opuesto al signo de la tercera constante; se puede escribir, por ejemplo, λ = − 1, μ = ν = 1. ^{[nota 7]}

El estudio del efecto de la perturbación en el "modo de Kasner" se limita, por tanto, a un estudio del efecto de los términos que contienen λ en las ecuaciones de Einstein. Los espacios de tipo VIII y IX son los modelos más adecuados para dicho estudio. Puesto que las 3 cantidades λ, μ, ν en esos tipos de Bianchi difieren de cero, la condición λ = 0 no se cumple independientemente de qué dirección l , m , n tenga dependencia temporal de ley de potencia negativa .

Las ecuaciones de Einstein para los modelos espaciales Tipo VIII y Tipo IX son ^{[46] [nota 2]}

(los componentes restantes , , , , , son idénticos a ceros). Estas ecuaciones contienen sólo funciones del tiempo; esta es una condición que debe cumplirse en todos los espacios homogéneos. Aquí, las ecuaciones 22 y 23 son exactas y su validez no depende de lo cerca que uno esté de la singularidad en t = 0. ^{[nota 8]} ${\displaystyle R_{l}^{0}}$ ${\displaystyle R_{m}^{0}}$ ${\displaystyle R_{n}^{0}}$ ${\displaystyle R_{l}^{m}}$ ${\displaystyle R_{l}^{n}}$ ${\displaystyle R_{m}^{n}}$

Las derivadas temporales en las ecuaciones 22 y 23 toman una forma más simple si ΰ , b , c se sustituyen por sus logaritmos α, β, γ:

sustituyendo la variable t por τ según:

Entonces (los subíndices denotan diferenciación por τ):

Sumando las ecuaciones ec. 26 y sustituyendo en el lado izquierdo la suma (α + β + γ) _{τ τ} según la ec. 27 , se obtiene una ecuación que contiene sólo primeras derivadas que es la primera integral del sistema ec. 26 :

Esta ecuación cumple el papel de una condición de unión impuesta al estado inicial de la ecuación 26. El modo de Kasner de la ecuación 8 es una solución de la ecuación 26 cuando se ignoran todos los términos en los lados derechos. Pero tal situación no puede continuar (en t → 0) indefinidamente porque entre esos términos siempre hay algunos que crecen. Por lo tanto, si la potencia negativa está en la función a ( t ) ( p _l = p ₁ ) entonces la perturbación del modo de Kasner surgirá por los términos λ ² a ⁴ ; el resto de los términos decrecerán con la disminución de t . Si solo se dejan los términos crecientes en los lados derechos de la ecuación 26 , se obtiene el sistema:

(compárese la ecuación 16 ; a continuación se sustituye λ ² = 1). La solución de estas ecuaciones debe describir la evolución métrica desde el estado inicial, en el que se describe por la ecuación 8 con un conjunto dado de potencias (con p _l < 0); sea p _l = р ₁ , p _m = р ₂ , p _n = р ₃ de modo que

Entonces

donde Λ es constante. Las condiciones iniciales para la ecuación 29 se redefinen como

Las ecuaciones 29 se integran fácilmente; la solución que satisface la condición 32 es

donde b ₀ y c ₀ son dos constantes más.

Se puede ver fácilmente que la asintótica de las funciones ecuación 33 en t → 0 es ecuación 30. Las expresiones asintóticas de estas funciones y la función t (τ) en τ → −∞ son ^{[nota 9]}

${\displaystyle a\sim e^{-\Lambda p_{1}\tau },\ b\sim e^{\Lambda (p_{2}+2p_{1})\tau },\ c\sim e^{\Lambda (p_{3}+2p_{1})\tau },\ t\sim e^{\Lambda (1+2p_{1})\tau }.}$

Expresando a , b , c como funciones de t , se tiene

dónde

Entonces

Lo anterior muestra que la perturbación actúa de tal manera que cambia un modo de Kasner con otro modo de Kasner, y en este proceso la potencia negativa de t cambia de dirección l a dirección m : si antes era p _l < 0, ahora es p' _m < 0. Durante este cambio la función a ( t ) pasa por un máximo y b ( t ) pasa por un mínimo; b , que antes era decreciente, ahora aumenta: a de creciente se vuelve decreciente; y el decreciente c ( t ) decrece aún más. La perturbación misma (λ ² a ^4α en la ecuación 29 ), que antes era creciente, ahora comienza a decrecer y desaparecer. La evolución posterior causa de manera similar un aumento en la perturbación de los términos con μ ² (en lugar de λ ² ) en la ecuación 26 , siguiente cambio del modo de Kasner, y así sucesivamente.

Es conveniente escribir la regla de sustitución de potencia de la ecuación 35 con la ayuda de la parametrización de la ecuación 5 :

La mayor de las dos potencias positivas sigue siendo positiva.

BKL llama a este cambio de potencia negativa entre direcciones una época de Kasner . La clave para entender el carácter de la evolución métrica al acercarse a la singularidad es exactamente este proceso de alternancia de épocas de Kasner con cambio de potencias p _l , p _m , p _n por la regla de la ecuación 37 .

Las alternancias sucesivas de la ecuación 37 con el cambio de la potencia negativa p ₁ entre las direcciones l y m (épocas de Kasner) continúan por agotamiento de toda la parte de la u inicial hasta el momento en que u < 1. El valor u < 1 se transforma en u > 1 según la ecuación 6 ; en este momento la potencia negativa es p _l o p _m mientras que p _n se convierte en el menor de dos números positivos ( p _n = p ₂ ). La siguiente serie de épocas de Kasner cambia entonces la potencia negativa entre las direcciones n y l o entre n y m . En un valor inicial arbitrario ( irracional ) de u este proceso de alternancia continúa sin límites. ^{[nota 10]}

En la solución exacta de las ecuaciones de Einstein, las potencias p _l , p _m , p _n pierden su sentido preciso original. Esta circunstancia introduce cierta "borrosidad" en la determinación de estos números (y junto con ellos, en el parámetro u ) que, aunque pequeña, hace que carezca de sentido el análisis de cualesquiera valores definidos (por ejemplo, racionales ) de u . Por lo tanto, sólo estas leyes que se refieren a valores arbitrarios irracionales de u tienen algún significado particular.

Los períodos mayores en los que las escalas de las distancias espaciales a lo largo de dos ejes oscilan mientras que las distancias a lo largo del tercer eje disminuyen monótonamente, se llaman eras ; los volúmenes disminuyen según una ley próxima a ~ t . En la transición de una era a la siguiente, la dirección en la que las distancias disminuyen monótonamente , cambia de un eje a otro. El orden de estas transiciones adquiere el carácter asintótico de un proceso aleatorio . El mismo orden aleatorio también es característico de la alternancia de las longitudes de las eras sucesivas (por longitud de era, BKL entiende el número de épocas de Kasner que contiene una era, y no un intervalo de tiempo).

A cada era ( s -ésima era) corresponden una serie de valores del parámetro u partiendo del mayor, , y pasando por los valores − 1, − 2, ..., llegando al menor, < 1. Entonces ${\displaystyle u_{\max }^{(s)}}$ ${\displaystyle u_{\max }^{(s)}}$ ${\displaystyle u_{\max }^{(s)}}$ ${\displaystyle u_{\min }^{(s)}}$

es decir, k ^{( s )} = [ ] donde los corchetes significan la parte entera del valor. El número k ^{( s )} es la longitud de la era, medida por el número de épocas de Kasner que contiene la era. Para la siguiente era ${\displaystyle u_{\max }^{(s)}}$

En la serie ilimitada de números u , compuesta por estas reglas, hay valores infinitesimalmente pequeños (pero nunca cero) x ^{( s )} y longitudes correspondientemente infinitamente grandes k ^{( s )} .

Las series de eras se vuelven más densas a medida que se aproximan a t = 0. Sin embargo, la variable natural para describir el curso temporal de esta evolución no es el tiempo mundial t , sino su logaritmo, ln t , por el cual todo el proceso de alcanzar la singularidad se extiende hasta −∞.

Según la ecuación 33 , una de las funciones a , b , c , que pasa por un máximo durante una transición entre épocas de Kasner, en el pico de su máximo es

donde se supone que a _max es grande comparado con b ₀ y c ₀ ; en la ecuación 38 u es el valor del parámetro en la época de Kasner antes de la transición. Se puede ver desde aquí que los picos de máximos consecutivos durante cada era se reducen gradualmente. De hecho, en la siguiente época de Kasner este parámetro tiene el valor u' = u − 1, y Λ se sustituye de acuerdo con la ecuación 36 con Λ' = Λ(1 − 2| p ₁ ( u )|). Por lo tanto, la relación de 2 máximos consecutivos es

${\displaystyle {\frac {a'_{\max }}{a_{\max }}}=\left[{\frac {p_{1}(u-1)}{p_{1}(u)}}\left(1-2|p_{1}(u)|\right)\right]^{\frac {1}{2}};}$

Y finalmente

Las anteriores son soluciones a ecuaciones de Einstein en el vacío. En cuanto al modo puro de Kasner, la materia no cambia las propiedades cualitativas de esta solución y puede escribirse en ella sin tener en cuenta su reacción en el campo. Sin embargo, si uno hace esto para el modelo en discusión, entendido como una solución exacta de las ecuaciones de Einstein, la imagen resultante de la evolución de la materia no tendría un carácter general y sería específica para la alta simetría inminente al modelo actual. Matemáticamente, esta especificidad está relacionada con el hecho de que para la geometría espacial homogénea discutida aquí, los componentes del tensor de Ricci son idénticamente ceros y, por lo tanto, las ecuaciones de Einstein no permitirían el movimiento de la materia (lo que da componentes del tensor de energía-momento de tensión no nulos ). En otras palabras, el marco sincrónico también debe estar en co-movimiento con respecto a la materia. Si uno sustituye en la ecuación 19 u _α = 0, u ⁰ = 1, se convierte en ε ~ ( abc ) ^−4/3 ~ t ^−4/3 . ${\displaystyle R_{\alpha }^{0}}$ ${\displaystyle T_{\alpha }^{0}}$

Esta dificultad se evita si se incluyen en el modelo sólo los términos mayores de la métrica límite (en t → 0) y se escribe en él una materia con una distribución inicial arbitraria de densidades y velocidades. Entonces el curso de la evolución de la materia está determinado por sus leyes generales de movimiento, ecuación 17 y ecuación 18, que dan como resultado la ecuación 21. Durante cada época de Kasner, la densidad aumenta según la ley

donde p ₃ es, como arriba, el mayor de los números p ₁ , p ₂ , p ₃ . La densidad de materia aumenta monótonamente durante toda la evolución hacia la singularidad.

Evolución métrica

Valores u muy grandes corresponden a potencias de Kasner

que están cerca de los valores (0, 0, 1). Dos valores que están cerca de cero, también están cerca uno del otro, y por lo tanto los cambios en dos de los tres tipos de "perturbaciones" (los términos con λ, μ y ν en los lados derechos de la ecuación 26 ) también son muy similares. Si al comienzo de una era tan larga estos términos están muy cerca en valores absolutos en el momento de transición entre dos épocas de Kasner (o se hacen artificialmente así asignando condiciones iniciales), entonces permanecerán cerca durante la mayor parte de la duración de toda la era. En este caso (BKL lo llama el caso de pequeñas oscilaciones ), el análisis basado en la acción de un tipo de perturbaciones se vuelve incorrecto; uno debe tener en cuenta el efecto simultáneo de dos tipos de perturbaciones.

Dos perturbaciones

Consideremos una era larga, durante la cual dos de las funciones a , b , c (sean a y b ) experimentan pequeñas oscilaciones mientras que la tercera función ( c ) decrece monótonamente. La última función rápidamente se vuelve pequeña; consideremos la solución justo en la región donde uno puede ignorar c en comparación con a y b . Los cálculos se realizan primero para el modelo espacial Tipo IX sustituyendo en consecuencia λ = μ = ν = 1. ^[43]

Después de ignorar la función c , las primeras 2 ecuaciones ec. 26 dan

y la ecuación 28 se puede utilizar como una tercera ecuación, que toma la forma

La solución de la ecuación 44 se escribe en la forma

${\displaystyle \alpha +\beta ={\frac {2a_{0}^{2}}{\xi _{0}}}\left(\tau -\tau _{0}\right)+2\ln a_{0},}$

donde α ₀ , ξ ₀ son constantes positivas y τ ₀ es el límite superior de la era para la variable τ. Es conveniente introducir además una nueva variable (en lugar de τ)

Entonces

Las ecuaciones 45 y 46 se transforman introduciendo la variable χ = α − β:

La disminución de τ de τ ₀ a −∞ corresponde a una disminución de ξ de ξ ₀ a 0. La era larga con a y b cercanos (es decir, con χ pequeño), considerada aquí, se obtiene si ξ ₀ es una cantidad muy grande. De hecho, en ξ grande la solución de la ecuación 49 en la primera aproximación por 1/ξ es

donde A es constante; el multiplicador hace que χ sea una cantidad pequeña, por lo que puede sustituirse en la ecuación 49 por sh 2χ ≈ 2χ. ^{[nota 11]} ${\displaystyle {\tfrac {1}{\sqrt {\xi }}}}$

De la ecuación 50 se obtiene

${\displaystyle \gamma _{\xi }={\frac {1}{4}}\xi \left(2\chi _{\xi }^{2}+\chi ^{2}\right)=A^{2},\ \gamma =A^{2}\left(\xi -\xi _{0}\right)+\mathrm {const} .}$

Después de determinar α y β a partir de la ecuación 48 y la ecuación 51 y expandir e ^α y e ^β en serie de acuerdo con la aproximación anterior, se obtiene finalmente: ^{[nota 12]}

La relación entre la variable ξ y el tiempo t se obtiene por integración de la definición dt = abc d τ que da

La constante c ₀ (el valor de с en ξ = ξ ₀ ) debería ser ahora c ₀ α ₀ · ${\displaystyle \ll }$

Espacio de tipo VIII (abierto) de Bianchi sometido a una dinámica BKL (Mixmaster) caótica cercana a la singularidad según las reglas de la ecuación 35 con . La singularidad se encuentra en el punto central de la superficie hiperboloide. ${\displaystyle u={\sqrt {13}}}$

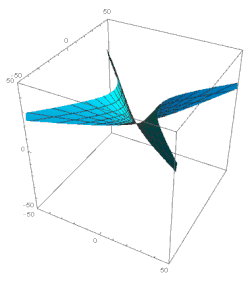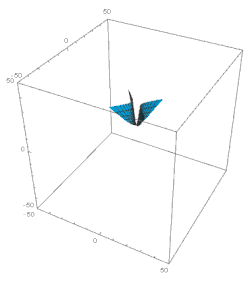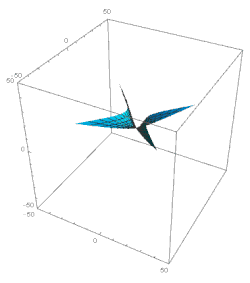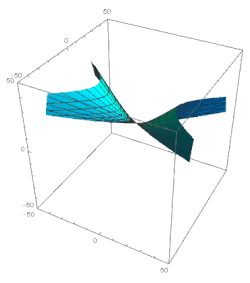
Consideremos ahora el dominio ξ 1. Aquí los términos principales en la solución de la ecuación 49 son: ${\displaystyle \ll }$

${\displaystyle \chi =\alpha -\beta =k\ln \xi +\mathrm {const} ,\,}$

donde k es una constante en el rango − 1 < k < 1; esta condición asegura que el último término en la ecuación 49 sea pequeño (sh 2χ contiene ξ ^{2 k} y ξ ^{−2 k} ). Luego, después de determinar α, β y t , se obtiene

Este es nuevamente un modo de Kasner con la potencia t negativa presente en la función c ( t ). ^{[nota 13]}

Estos resultados muestran una evolución cualitativamente similar a la descrita anteriormente. Durante un largo período de tiempo que corresponde a un gran valor decreciente de ξ, las dos funciones a y b oscilan, permaneciendo cercanas en magnitud ; en el mismo tiempo, ambas funciones a y b decrecen lentamente ( ). El período de oscilaciones es constante por la variable ξ : Δξ = 2π (o, lo que es lo mismo, con un período constante por tiempo logarítmico: Δ ln t = 2π Α ² ). La tercera función, c , decrece monótonamente por una ley cercana a c = c ₀ t / t ₀ . ${\displaystyle {\tfrac {a-b}{a}}\sim {\tfrac {1}{\sqrt {\xi }}}}$ ${\displaystyle \sim {\sqrt {\xi }}}$

Esta evolución continúa hasta que ξ ≈1 y las fórmulas ec. 52 y ec. 53 ya no son aplicables. Su duración temporal corresponde al cambio de t desde t ₀ hasta el valor t ₁ , relacionado con ξ ₀ según

La relación entre ξ y t durante este tiempo se puede presentar en la forma

Después de eso, como se ve en la ecuación 55 , la función decreciente c comienza a aumentar mientras que las funciones a y b comienzan a disminuir. Esta época de Kasner continúa hasta que los términos c ² / a ² b ² en la ecuación 22 se convierten en ~ t ² y comienza una siguiente serie de oscilaciones.

La ley para el cambio de densidad durante la larga era en discusión se obtiene mediante la sustitución de la ecuación 52 en la ecuación 20 :

Cuando ξ cambia de ξ ₀ a ξ ≈1, la densidad aumenta veces. ${\displaystyle \xi _{0}^{2}}$

Se debe destacar que aunque la función c ( t ) cambia según una ley, cercana a c ~ t , la ecuación métrica 52 no corresponde a una métrica de Kasner con potencias (0, 0, 1). Esta última corresponde a una solución exacta encontrada por Taub ^[47] que está permitida por las ecuaciones 26 – 27 y en la que

donde p , δ ₁ , δ ₂ son constantes. En la región asintótica τ → −∞, se puede obtener de aquí a = b = const, c = const. t después de la sustitución е ^рτ = t . En esta métrica, la singularidad en t = 0 no es física.

Describamos ahora el estudio análogo del modelo Tipo VIII, sustituyendo en las ecuaciones 26' –' 28 λ = −1, μ = ν = 1. ^[44]

Si durante la era larga, la función monótonamente decreciente es a , nada cambia en el análisis anterior: ignorando a ² en el lado derecho de las ecuaciones 26 y 28 , se vuelve a las mismas ecuaciones 49 y 50 (con notación alterada). Sin embargo, ocurren algunos cambios si la función monótonamente decreciente es b o c ; sea c .

Como antes, se tiene la ecuación 49 con los mismos símbolos y, por lo tanto, las expresiones anteriores ecuación 52 para las funciones a (ξ) y b (ξ), pero la ecuación 50 se reemplaza por

El término principal en general ξ ahora se convierte en

${\displaystyle \gamma _{\xi }\approx {\frac {1}{8}}\xi \cdot 2,\quad \gamma \approx {\frac {1}{8}}\left(\xi ^{2}-\xi _{0}^{2}\right),}$

de modo que

El valor de c en función del tiempo t es nuevamente c = c ₀ t / t ₀ pero la dependencia temporal de ξ cambia. La duración de una era larga depende de ξ ₀ según

Por otra parte, el valor ξ ₀ determina el número de oscilaciones de las funciones a y b durante una era (igual a ξ ₀ /2π). Dada la longitud de una era en tiempo logarítmico (es decir, con una razón dada t ₀ / t ₁ ), el número de oscilaciones para el Tipo VIII será, en términos generales, menor que para el Tipo IX. Para el período de oscilaciones se obtiene ahora Δ ln t = πξ/2; al contrario que en el Tipo IX, el período no es constante a lo largo de la larga era, y disminuye lentamente junto con ξ.

El dominio de los pequeños tiempos

Las eras largas violan el curso "regular" de la evolución, lo que dificulta el estudio de la evolución de intervalos de tiempo que abarcan varias eras. Sin embargo, se puede demostrar que estos casos "anormales" aparecen en la evolución espontánea del modelo hacia un punto singular en los tiempos asintóticamente pequeños t a distancias suficientemente grandes de un punto de partida con condiciones iniciales arbitrarias. Incluso en eras largas, ambas funciones oscilatorias durante las transiciones entre épocas de Kasner siguen siendo tan diferentes que la transición ocurre bajo la influencia de una sola perturbación. Todos los resultados de esta sección se relacionan igualmente con modelos de los tipos VIII y IX. ^[48]

Durante cada época de Kasner abc = Λ t , es decir α + β + γ = ln Λ + ln t . Al cambiar de una época (con un valor dado del parámetro u ) a la siguiente época, la constante Λ se multiplica por 1 + 2 p ₁ = (1 – u + u ² )/(1 + u + u ² ) < 1. Por lo tanto, tiene lugar una disminución sistemática de Λ. Pero es esencial que el valor medio (con respecto a las longitudes k de las eras) de toda la variación de ln Λ durante una era sea finito. En realidad, la divergencia del valor medio podría deberse solo a un aumento demasiado rápido de esta variación con el aumento de k . Para un valor grande del parámetro u , ln(1 + 2 p ₁ ) ≈ −2/ u . Para un k grande, el valor máximo u ^(max) = k + x ≈ k. Por lo tanto, la variación total de ln Λ durante una era está dada por una suma de la forma

${\displaystyle \sum \ln \left(1+2p_{1}\right)=\dots +{\frac {1}{k-2}}+{\frac {1}{k-1}}+{\frac {1}{k}}}$

con sólo los términos que corresponden a grandes valores de u escritos. Cuando k aumenta esta suma aumenta como ln k . Pero la probabilidad de aparición de una era de una gran duración k disminuye como 1/ k ₂ según la ecuación 76 ; por lo tanto, el valor medio de la suma anterior es finito. En consecuencia, la variación sistemática de la cantidad ln Λ a lo largo de un gran número de eras será proporcional a este número. Pero se ve en la ecuación 85 que con t → 0 el número s aumenta simplemente como ln |ln t |. Por lo tanto, en el límite asintótico de t arbitrariamente pequeño, el término ln Λ puede de hecho despreciarse en comparación con ln t . En esta aproximación ^{[nota 14]}

donde Ω denota el "tiempo logarítmico"

y el proceso de transición de época puede considerarse como una serie de breves destellos temporales. Las magnitudes de los máximos de las funciones de escala oscilantes también están sujetas a una variación sistemática. De la ecuación 39 para u ≫ 1 se deduce que . De la misma manera que se hizo anteriormente para la cantidad ln Λ, se puede deducir que la disminución media en la altura de los máximos durante una era es finita y la disminución total a lo largo de un gran número de eras aumenta con t → 0 simplemente como ln Ω. Al mismo tiempo, la disminución de los mínimos, y por la misma razón el aumento de la amplitud de las oscilaciones, proceden ( ecuación 77 ) proporcional a Ω. En correspondencia con la aproximación adoptada, se desprecia la disminución de los máximos en comparación con el aumento de las amplitudes, de modo que α _max = 0, β _max = 0, γ _max = 0 para los valores máximos de todas las funciones oscilantes y las cantidades α, β, γ pasan sólo por valores negativos que están conectados entre sí en cada instante de tiempo por la relación ecuación 63 . ${\displaystyle a_{\max }^{\prime }-a_{\max }\approx -1/2u}$

Variación de α, β y γ en función del tiempo logarítmico Ω durante una era. Las líneas discontinuas verticales indican alteraciones de las épocas de Kasner, correspondientes a los segmentos lineales de las curvas. En la parte superior se indican los valores del parámetro u que determinan los exponentes de Kasner. La última época tiene una duración mayor si x es pequeño. En la primera época de la siguiente era, γ comienza a aumentar y α se convierte en una función monótonamente decreciente.

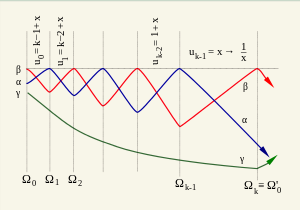
Considerando tal cambio instantáneo de épocas, los períodos de transición se ignoran como pequeños en comparación con la longitud de la época; esta condición se cumple en realidad. ^{[nota 15]} El reemplazo de los máximos α, β y γ con ceros requiere que las cantidades ln (| p ₁ |Λ) sean pequeñas en comparación con las amplitudes de oscilaciones de las respectivas funciones. Como se mencionó anteriormente, durante las transiciones entre eras, los valores | p ₁ | pueden llegar a ser muy pequeños mientras que su magnitud y probabilidad de ocurrencia no están relacionadas con las amplitudes de oscilación en el momento respectivo. Por lo tanto, en principio, es posible alcanzar valores | p ₁ | tan pequeños que se viole la condición anterior (máximos cero). Tal caída drástica de α _max puede conducir a varias situaciones especiales en las que la transición entre épocas de Kasner por la regla de la ecuación 37 se vuelve incorrecta (incluidas las situaciones descritas anteriormente). Estas situaciones "peligrosas" podrían romper las leyes utilizadas para el análisis estadístico a continuación. Sin embargo, como se mencionó, la probabilidad de tales desviaciones converge asintóticamente a cero; esta cuestión se analizará más adelante.

Considere una era que contiene k épocas de Kasner con un parámetro u que recorre los valores

y sean α y β las funciones oscilantes durante esta era (Fig. 4). ^{[nota 16]}

Los momentos iniciales de las épocas de Kasner con parámetros u _n son Ω _n . En cada momento inicial, uno de los valores α o β es cero, mientras que el otro tiene un mínimo. Los valores α o β en mínimos consecutivos, es decir, en momentos Ω _n son

(sin distinguir mínimos α y β). Los valores δ _n que miden esos mínimos en las respectivas unidades Ω _n pueden oscilar entre 0 y 1. La función γ decrece monótonamente durante esta era; según la ecuación 63 su valor en el momento Ω _n es

Durante la época que comienza en el momento Ω _n y termina en el momento Ω _{n +1} una de las funciones α o β aumenta desde −δ _n Ω _n hasta cero mientras que la otra decrece desde 0 hasta −δ _{n +1} Ω _{n +1} por leyes lineales, respectivamente:

${\displaystyle \mathrm {const} +|p_{1}(u_{n})|\Omega \,}$y ${\displaystyle \mathrm {const} -p_{2}(u_{n})\Omega \,}$

resultando en la relación de recurrencia

y para la longitud de la época logarítmica

donde, para abreviar, f ( u ) = 1 + u + u ² . La suma de las n longitudes de época se obtiene mediante la fórmula

De la ecuación 68 se desprende que |α _n+1 | > |α _n |, es decir, las amplitudes de oscilación de las funciones α y β aumentan durante toda la era aunque los factores δ _n puedan ser pequeños. Si el mínimo al comienzo de una era es profundo, los mínimos siguientes no se harán más superficiales; en otras palabras, el residuo |α — β| en el momento de la transición entre las épocas de Kasner sigue siendo grande. Esta afirmación no depende de la longitud de la era k porque las transiciones entre épocas están determinadas por la regla común de la ecuación 37 también para las eras largas.

La última amplitud de oscilación de las funciones α o β en una era dada está relacionada con la amplitud de la primera oscilación por la relación |α _{k −1} | = |α ₀ | ( k + x ) / (1 + x ). Incluso en k ' s tan pequeños como varias unidades x puede ignorarse en comparación con k de modo que el aumento de las amplitudes de oscilación de α y β se vuelve proporcional a la longitud de la era. Para las funciones a = e ^α y b = e ^β esto significa que si la amplitud de sus oscilaciones al comienzo de una era era A ₀ , al final de esta era la amplitud se convertirá en . ${\displaystyle A_{0}^{k/(1+x)}}$

La longitud de las épocas de Kasner (en tiempo logarítmico) también aumenta dentro de una era dada; es fácil calcular a partir de la ecuación 69 que Δ _{n +1} > Δ _n . ^{[nota 17]} La ​​longitud total de la era es

(el término con 1/ x surge de la última, k -ésima, época cuya longitud es grande en x pequeño ; cf. Fig. 2). El momento Ω _n en el que termina la k -ésima época de una era dada es al mismo tiempo el momento Ω' ₀ del comienzo de la siguiente era.

En la primera época de Kasner de la nueva era, la función γ es la primera en ascender desde el valor mínimo γ _k = − Ω _k (1 − δ _k ) que alcanzó en la era anterior; este valor cumple el papel de amplitud de partida δ' ₀ Ω' ₀ para la nueva serie de oscilaciones. Se obtiene fácilmente que:

Es evidente que δ' ₀ Ω' ₀ > δ ₀ Ω ₀ . Incluso con valores k no muy grandes, el aumento de amplitud es muy significativo: la función c = e ^γ comienza a oscilar desde una amplitud . Dejamos de lado por ahora la cuestión de los casos "peligrosos" antes mencionados de reducción drástica del límite superior de oscilación. ${\displaystyle A_{0}'\sim A_{0}^{k^{2}}}$

Según la ecuación 40, el aumento de la densidad de materia durante las primeras ( k − 1) épocas viene dado por la fórmula

${\displaystyle \ln \left({\frac {\varepsilon _{n+1}}{\varepsilon _{n}}}\right)=2\left[1-p_{3}(u_{n})\right]\Delta _{n+1}.}$

Para la última época k de una era dada, en u = x < 1 la mayor potencia es p ₂ ( x ) (no p ₃ ( x ) ). Por lo tanto, para el aumento de densidad a lo largo de toda la era se obtiene

Por lo tanto, incluso con valores k no muy grandes , . Durante la siguiente era (con una longitud k ' ) la densidad aumentará más rápido debido a la mayor amplitud inicial A ₀ ': , etc. Estas fórmulas ilustran el pronunciado aumento de la densidad de la materia. ${\displaystyle \varepsilon _{0}'/\varepsilon _{0}\sim A_{0}^{2k}}$ ${\displaystyle \varepsilon _{0}''/\varepsilon _{0}'\sim A_{0}'^{2k''}\sim A_{0}^{2k^{2}k'}}$

Análisis estadístico cerca de la singularidad

La sucesión de longitudes de eras k ^{( s )} , medida por el número de épocas de Kasner contenidas en ellas, adquiere asintóticamente el carácter de un proceso aleatorio. Lo mismo se aplica también a la sucesión de los intercambios de los pares de funciones oscilantes al pasar de una era a la siguiente (depende de si los números k ^{( s )} son pares o impares). Una fuente de esta estocasticidad es la regla de las ecuaciones 41-42 según la cual la transición de una era a la siguiente está determinada en una sucesión numérica infinita de valores u . Esta regla establece, en otras palabras, que si toda la sucesión infinita comienza con un cierto valor inicial , entonces las longitudes de las eras k ⁽⁰⁾ , k ⁽¹⁾ , ..., son los números en el desarrollo fraccionario continuo ${\displaystyle u_{\max }^{(0)}=k^{(0)}+x^{(0)}}$

Esta expansión corresponde a la transformación de aplicación del intervalo [0, 1] sobre sí mismo por la fórmula Tx = {1/ x }, es decir, x _{s +1} = {1/ x _s }. Esta transformación pertenece a las llamadas transformaciones de expansión del intervalo [0, 1], es decir, transformaciones x → f ( x ) con | f′ ( x )| > 1. Tales transformaciones poseen la propiedad de inestabilidad exponencial: si tomamos inicialmente dos puntos cercanos, su distancia mutua aumenta exponencialmente bajo las iteraciones de las transformaciones. Es bien sabido que la inestabilidad exponencial conduce a la aparición de fuertes propiedades estocásticas.

Es posible pasar a una descripción probabilística de dicha secuencia considerando no un valor inicial definido x ⁽⁰⁾ sino los valores x ⁽⁰⁾ = x distribuidos en el intervalo de 0 a 1 de acuerdo con una cierta ley de distribución probabilística w ₀ ( x ). Entonces los valores de x ^(s) que terminan cada era también tendrán distribuciones que siguen ciertas leyes w _s (x) . Sea w _s (x)dx la probabilidad de que la s -ésima era termine con el valor que se encuentra en un intervalo especificado dx . ${\displaystyle u_{\max }^{(s)}=x}$

El valor x ^(s) = x , que pone fin a la era s -ésima, puede resultar de valores iniciales (para esta era) , donde k = 1, 2, ...; estos valores de corresponden a los valores x ^{( s –1)} = 1/( k + x ) para la era precedente. Teniendo esto en cuenta, se puede escribir la siguiente relación de recurrencia, que expresa la distribución de las probabilidades w _s (x) en términos de la distribución w _{s –1} ( x ): ${\displaystyle u_{\max }^{(s)}=x+k}$ ${\displaystyle u_{\max }^{(s)}}$

${\displaystyle w_{s}(x)dx=\sum _{k=1}^{\infty }w_{s-1}\left({\frac {1}{k+x}}\right)\left\vert d{\frac {1}{k+x}}\right\vert }$

o

Si la distribución w _s ( x ) tiende con el aumento de s a una distribución límite estacionaria (independiente de s ) w ( x ), entonces esta última debería satisfacer una ecuación obtenida de la ecuación 73c al eliminar los índices de las funciones w _{s −1} ( x ) y w _s ( x ). Esta ecuación tiene una solución

(normalizado a la unidad y llevado al primer orden de x ). ^{[nota 18]}

Para que la era s -ésima tenga una longitud k , la era anterior debe terminar con un número x en el intervalo entre 1/( k + 1) y 1/ k . Por lo tanto, la probabilidad de que la era tenga una longitud k es igual a (en el límite estacionario)

En valores grandes de k

Al relacionar las propiedades estadísticas del modelo cosmológico con las propiedades ergódicas de la transformación x _{s + 1} = {1/ x _s } debe mencionarse un punto importante. En una secuencia infinita de números x construida de acuerdo con esta regla, se observarán valores arbitrariamente pequeños (pero nunca nulos) de x correspondientes a longitudes arbitrariamente grandes k. Tales casos pueden (¡de ninguna manera necesariamente!) dar lugar a ciertas situaciones específicas en las que la noción de eras, como de secuencias de épocas de Kasner que se intercambian entre sí de acuerdo con la regla eq. 37 , pierde su significado (aunque el modo oscilatorio de evolución del modelo aún persiste). Una situación "anómala" de este tipo puede manifestarse, por ejemplo, en la necesidad de retener en el lado derecho de la eq. 26 términos no sólo con una de las funciones a , b , c (digamos, a ⁴ ), como es el caso en el intercambio "regular" de las épocas de Kasner, sino simultáneamente con dos de ellas (digamos, a ⁴ , b ⁴ , a ² b ² ).

Al salir de una serie de oscilaciones "anómalas" se restablece una sucesión de eras regulares. El análisis estadístico del comportamiento del modelo, que se basa enteramente en iteraciones regulares de las transformaciones de la ecuación 42, se corrobora mediante un teorema importante: la probabilidad de aparición de casos anómalos tiende asintóticamente a cero a medida que el número de iteraciones s → ∞ (es decir, el tiempo t → 0), lo que se demuestra al final de esta sección. La validez de esta afirmación se debe en gran medida a una tasa muy rápida de aumento de las amplitudes de oscilación durante cada era y especialmente en la transición de una era a la siguiente.

El proceso de relajación del modelo cosmológico al régimen estadístico "estacionario" (con t → 0 a partir de un "instante inicial" dado) es menos interesante, sin embargo, que las propiedades de este régimen mismo, teniendo debidamente en cuenta las leyes concretas de la variación de las características físicas del modelo durante las eras sucesivas.

Una idea de la velocidad a la que se establece la distribución estacionaria se obtiene del siguiente ejemplo. Supongamos que los valores iniciales x ⁽⁰⁾ se distribuyen en un intervalo estrecho de ancho δ x ⁽⁰⁾ alrededor de un número definido. A partir de la relación de recurrencia de la ecuación 73c (o directamente de la expansión de la ecuación 73a ) es fácil concluir que los anchos de las distribuciones w _s ( x ) (alrededor de otros números definidos) serán entonces iguales a

(esta expresión es válida sólo en la medida en que defina cantidades δ x ^(s) ≪ 1).

El valor medio , calculado a partir de esta distribución, diverge logarítmicamente. Para una secuencia, cortada en un número muy grande, pero todavía finito N , se tiene . La utilidad de la media en este caso es muy limitada debido a su inestabilidad: debido a la lenta disminución de W ( k ), las fluctuaciones en k divergen más rápido que su media. Una característica más adecuada de esta secuencia es la probabilidad de que un número elegido al azar de ella pertenezca a una era de longitud K donde K es grande. Esta probabilidad es ln K / ln N . Es pequeña si . A este respecto, se puede decir que un número elegido al azar de la secuencia dada pertenece a la era larga con una alta probabilidad. ${\displaystyle {\bar {k}}}$ ${\displaystyle {\bar {k}}\sim \ln N}$ ${\displaystyle 1\ll K\ll N}$

Es conveniente promediar expresiones que dependen simultáneamente de k ^{( s )} y x ^{( s )} . Como ambas cantidades se derivan de la misma cantidad x ^{( s –1)} (que termina la era precedente), de acuerdo con la fórmula k ^{( s )} + x ^{( s )} = 1/ x ^{( s –1)} , sus distribuciones estadísticas no pueden considerarse independientes. La distribución conjunta W _s ( k , x ) dx de ambas cantidades se puede obtener a partir de la distribución w _{s –1} ( x ) dx haciendo en esta última la sustitución x → 1/( x + k ). En otras palabras, la función W _s ( k , x ) está dada por la misma expresión bajo el signo de suma en el lado derecho de la ecuación 73c . En el límite estacionario, tomando w de la ecuación 74 , se obtiene

La suma de esta distribución sobre k nos lleva de nuevo a la ecuación 74 , y la integración con respecto a dx a la ecuación 75 .

Las fórmulas recurrentes que definen las transiciones entre eras se reescriben con el índice s que numera las eras sucesivas (¡no las épocas de Kasner en una era dada!), comenzando desde alguna era ( s = 0) definida como inicial. Ω ^{( s )} y ε ^{( s )} son, respectivamente, el momento inicial y la densidad de materia inicial en la s -ésima era; δ ^{( s )} Ω ^{( s )} es la amplitud de oscilación inicial de ese par de funciones α, β, γ, que oscila en la era dada: k ^{( s )} es la longitud de la s -ésima era, y x ^{( s )} determina la longitud (número de épocas de Kasner) de la siguiente era según k ^{( s +1)} = [1/ x ^{( s )} ]. Según las ecuaciones 71 – 73

(ξ ^{( s )} se introduce en la ecuación 77 para su uso posterior).

Las cantidades δ ^{( s )} tienen una distribución estadística estacionaria estable P (δ) y un valor medio estable (pequeñas fluctuaciones relativas). Para su determinación, KL ^[48] en coautoría con Ilya Lifshitz , hermano de Evgeny Lifshitz, utilizó (con las debidas reservas) un método aproximado basado en el supuesto de independencia estadística de la cantidad aleatoria δ ^{( s )} y de las cantidades aleatorias k ^{( s )} , x ^{( s )} . Para la función P (δ) se estableció una ecuación integral que expresaba el hecho de que las cantidades δ ^{( s +1)} y δ ^{( s )} interconectadas por la relación eq. 78 tienen la misma distribución; esta ecuación se resolvió numéricamente. En un trabajo posterior, Khalatnikov et al. ^[49] demostraron que la distribución P (δ) en realidad se puede encontrar exactamente mediante un método analítico (ver Fig. 5 ).

Para las propiedades estadísticas en el límite estacionario, es razonable introducir la llamada extensión natural de la transformación Tx = {1/ x } continuándola sin límite hasta índices negativos. Dicho de otro modo, se trata de una transición desde una secuencia infinita unilateral de los números ( x ₀ , x ₁ , x ₂ , ...), conectados por las igualdades Tx = {1/ x }, a una secuencia "doblemente infinita" X = (..., x ₋₁ , x ₀ , x ₁ , x ₂ , ...) de los números que están conectados por las mismas igualdades para todo –∞ < s < ∞. Por supuesto, dicha expansión no es única en el sentido literal de la palabra (ya que x _{s –1} no está determinado unívocamente por x _s ), pero todas las propiedades estadísticas de la secuencia extendida son uniformes en toda su longitud, es decir, son invariantes con respecto a un desplazamiento arbitrario (y x ₀ pierde su significado de condición "inicial"). La sucesión X es equivalente a una sucesión de números enteros K = (..., k ₋₁ , k ₀ , k ₁ , k ₂ , ...), construida por la regla k _s = [1/ x _{s –1} ]. Inversamente, todo número de X está determinado por los números enteros de K como fracción continua infinita.

(La conveniencia de introducir la notación con un índice desplazado en 1 se hará evidente a continuación). Para la notación concisa, la fracción continua se denota simplemente mediante la enumeración (entre corchetes) de sus denominadores; entonces la definición de puede escribirse como ${\displaystyle x_{s+1}^{+}}$ ${\displaystyle x_{s}^{+}}$

Las cantidades inversas se definen mediante una fracción continua con una secuencia retrógrada (en la dirección de índices decrecientes) de denominadores.

La relación de recurrencia de la ecuación 78 se transforma introduciendo temporalmente la notación η _s = (1 − δ _s )/δ _s . Entonces la ecuación 78 se puede reescribir como

${\displaystyle \eta _{s+1}={\frac {1}{\eta _{s}x_{s-1}+k_{s}}}}$

Por iteración se obtiene una fracción continua infinita

${\displaystyle \eta _{s+1}x_{s}=\left[k_{s},k_{s-1},\dots \right]=x_{s+1}^{-}}$

Por lo tanto y finalmente ${\displaystyle \eta _{s}=x_{s}^{-}/x_{s}^{+}}$

Esta expresión para δ _s contiene sólo dos (en lugar de las tres en ^[48] ) cantidades aleatorias y , cada una de las cuales asume valores en el intervalo [0, 1]. ${\displaystyle x_{s}^{+}}$ ${\displaystyle x_{s}^{-}}$

De la definición de la ecuación 79c se deduce que . Por lo tanto, el desplazamiento de toda la secuencia X en un paso hacia la derecha significa una transformación conjunta de las cantidades y de acuerdo con ${\displaystyle 1/x_{s}^{-}=x_{s}^{-}+k_{s}=x_{s}^{-}+\left[1/x_{s}^{+}\right]}$ ${\displaystyle x_{s}^{+}}$ ${\displaystyle x_{s}^{-}}$

Se trata de una aplicación biunívoca en el cuadrado unitario . Por lo tanto, ahora tenemos una transformación biunívoca de dos cantidades en lugar de una transformación no biunívoca Tx = {1/ x } de una cantidad.

Las cantidades y tienen una distribución estacionaria conjunta P ( x ⁺ , x ⁻ ). Como la ecuación 79e es una transformación biunívoca, la condición para que la distribución sea estacionaria se expresa simplemente mediante una ecuación de función ${\displaystyle x_{s}^{+}}$ ${\displaystyle x_{s}^{-}}$

donde J es el jacobiano de la transformación.

Un desplazamiento de la secuencia X en un paso da lugar a la siguiente transformación T del cuadrado unitario:

${\displaystyle x^{\prime }={\frac {1}{x}},\quad y^{\prime }={\frac {1}{{\frac {1}{x}}+y}}}$

(con , , cf. ecuación 79e ). La densidad P ( x , y ) define la medida invariante para esta transformación. Es natural suponer que P ( x , y ) es una función simétrica de x e y . Esto significa que la medida es invariante con respecto a la transformación S ( x , y ) = ( y , x ) y, por lo tanto, con respecto al producto ST con ST ( x , y ) = ( x″ , y″ ) y ${\displaystyle x\equiv x_{0}^{+}}$ ${\displaystyle y\equiv x_{0}^{-}}$

${\displaystyle x''={\frac {1}{{\frac {1}{x}}+y}},\quad y''={\frac {1}{x}}}$

Evidentemente ST tiene una primera integral H = 1/ x + y . En la recta H = const ≡ c la transformación tiene la forma

${\displaystyle {\frac {1}{x''}}=\left[{\frac {1}{x}}\right]+y=\left[{\frac {1}{x}}\right]+c-{\frac {1}{x}}=c-\left\{{\frac {1}{x}}\right\}}$

Por lo tanto, la densidad de medida invariante de ST debe tener la forma

${\displaystyle f(c)\ dc\ d{\frac {1}{x}}=f\left({\frac {1}{x}}+y\right){\frac {1}{x^{2}}}dx\ dy}$

Teniendo en cuenta la simetría P ( x , y )= P ( y , x ), esto se convierte en f ( c )= c ⁻² y, por lo tanto (después de la normalización)

(su integración sobre x ⁺ o x ^– produce la función w ( x ) eq. 74 ). La reducción de la transformación a una función biunívoca ya fue utilizada por Chernoff y Barrow ^[50] y obtuvieron una fórmula de la forma de la eq. 79g pero para otras variables; su artículo no contiene aplicaciones a los problemas que se consideran en Khalatnikov et al. ^[49]

La exactitud de la ecuación 79g se puede verificar también mediante un cálculo directo; el jacobiano de la transformación de la ecuación 79e es

${\displaystyle J={\frac {\partial \left(x_{s+1}^{+},x_{s+1}^{-}\right)}{\partial \left(x_{s}^{+},x_{s}^{-}\right)}}={\frac {\partial x_{s+1}^{+}}{\partial x_{s}^{+}}}{\frac {\partial x_{s+1}^{-}}{\partial x_{s}^{-}}}=\left({\frac {x_{s+1}^{+}}{x_{s}^{+}}}\right)^{2}}$

(en su cálculo hay que tener en cuenta que ). ${\displaystyle \left[1/x_{s}^{+}\right]+\left\{1/x_{s}^{+}\right\}=1/x_{s}^{+}}$

Función de distribución de probabilidad P (δ). Línea roja: función exacta de la ecuación 79h . Línea azul: solución aproximada de la ecuación integral en. ^[48] Ambas curvas parecen ser sorprendentemente similares y las medias de ambas distribuciones son 0,50. ^{[nota 19]}

Puesto que por la ecuación 79d δ _s se expresa en términos de las cantidades aleatorias x ⁺ y x ⁻ , el conocimiento de su distribución conjunta permite calcular la distribución estadística P (δ) integrando P ( x ⁺ , x ⁻ ) sobre una de las variables con un valor constante de δ. Debido a la simetría de la función de la ecuación 79g con respecto a las variables x ⁺ y x ⁻ , P (δ) = P (1 − δ), es decir, la función P (δ) es simétrica con respecto al punto δ = 1/2. Entonces

${\displaystyle P(\delta )\ d\delta =d\delta \int _{0}^{1}P\left(x^{+},{\frac {x^{+}\delta }{1-\delta }}\right)\left({\frac {\partial x^{-}}{\partial \delta }}\right)_{x^{+}}dx^{+}}$

Al evaluar esta integral (para 0 ≤ δ ≤ 1/2 y luego hacer uso de la simetría antes mencionada), finalmente

El valor medio = 1/2 es el resultado de la simetría de la función P (δ). Por lo tanto, el valor medio de la amplitud inicial (en cada época) de las oscilaciones de las funciones α, β, γ aumenta en Ω/2. ${\displaystyle {\bar {\delta }}}$

La relación estadística entre grandes intervalos de tiempo Ω y el número de eras s contenidas en ellos se encuentra mediante la aplicación repetida de la ecuación 77 :

Sin embargo, el promedio directo de esta ecuación no tiene sentido: debido a la lenta disminución de la función W ( k ) eq. 76 , los valores promedio de la cantidad exp ξ ^{( s )} son inestables en el sentido anterior – las fluctuaciones aumentan incluso más rápidamente que el valor medio en sí mismo con el aumento de la región de promedio. Esta inestabilidad se elimina tomando el logaritmo: el intervalo de tiempo "doblemente logarítmico"

se expresa por la suma de cantidades ξ ^{( p )} que tienen una distribución estadística estable. El valor medio de τ es . Para calcularlo , tenga en cuenta que la ecuación 77 se puede reescribir como ${\displaystyle {\bar {\tau }}=s{\bar {\xi }}}$ ${\displaystyle {\bar {\xi }}}$

Para la distribución estacionaria , y en virtud de la simetría de la función P (δ) también . Por lo tanto ${\displaystyle {\overline {\ln x_{s}}}={\overline {\ln x_{s-1}}}}$ ${\displaystyle {\overline {\ln \delta _{s}}}={\overline {\ln \left(\delta _{s+1}\right)}}}$

${\displaystyle {\bar {\xi }}=-2{\overline {\ln x}}=-2\int _{0}^{1}w(x)\ln x\ dx={\frac {\pi ^{2}}{6\ln 2}}=2.37}$

( w ( x ) de la ecuación 74 ). Por lo tanto

que determina el intervalo de tiempo medio doblemente logarítmico que contiene s eras sucesivas.

Para s grandes, el número de términos en la suma de la ecuación 81 es grande y, según los teoremas generales de la teoría ergódica, los valores de τ _s se distribuyen según la ley de Gauss con la densidad ${\displaystyle {\overline {\tau _{s}}}}$

El cálculo de la varianza D _τ es más complicado, ya que no solo se necesita conocer y sino también las correlaciones . El cálculo se puede simplificar reordenando los términos en la suma de la ecuación 81 . Al utilizar la ecuación 81a, la suma se puede reescribir como ${\displaystyle {\bar {\xi }}}$ ${\displaystyle {\overline {\xi ^{2}}}}$ ${\displaystyle {\overline {\xi _{p}\xi _{p\prime }}}}$

${\displaystyle \sum _{p=1}^{s}\xi _{p}=\ln \prod _{p=1}^{s}{\frac {\delta _{p}}{\left(1-\delta _{p+1}\right)x_{p}x_{p-1}}}=\ln \prod _{p=1}^{s}{\frac {\delta _{p}}{\left(1-\delta _{p}\right)x_{p-1}^{2}}}+\ln {\frac {x_{0}}{x_{s}}}+\ln {\frac {1-\delta _{1}}{1-\delta _{s+1}}}}$

Los dos últimos términos no aumentan con el aumento de s ; estos términos se pueden omitir ya que las leyes limitantes para s grandes son dominantes. Entonces

(se toma en cuenta la expresión ec. 79d para δ _p ). Con la misma precisión (es decir, hasta los términos que no aumentan con s ) la igualdad

es válida. En efecto, en virtud de la ecuación 79e

${\displaystyle x_{p+1}^{+}+{\frac {1}{x_{p+1}^{-}}}={\frac {1}{x_{p}^{+}}}+x_{p}^{-}}$

y por lo tanto

${\displaystyle \ln \left(1+x_{p+1}^{+}x_{p+1}^{-}\right)-\ln x_{p+1}^{-}=\ln \left(1+x_{p}^{+}x_{p}^{-}\right)-\ln x_{p}^{+}}$

Sumando esta identidad sobre p se obtiene la ecuación 82c . Finalmente, nuevamente con la misma precisión se cambia x _p bajo el signo de suma y, por lo tanto, se representa τ _s como ${\displaystyle x_{p}^{+}}$

La varianza de esta suma en el límite de s grande es

Se tiene en cuenta que en virtud de la homogeneidad estadística de la secuencia X las correlaciones dependen únicamente de las diferencias | p − p ′|. El valor medio ; el cuadrado medio ${\displaystyle {\overline {\eta _{p}\eta _{p\prime }}}}$ ${\displaystyle {\bar {\eta }}={\bar {\xi }}}$

${\displaystyle {\overline {\eta ^{2}}}=4\int _{0}^{1}w(x)\ln ^{2}x\ dx={\frac {6\xi (3)}{\ln 2}}=10.40}$

Teniendo en cuenta también los valores de las correlaciones con p = 1, 2, 3 (calculados numéricamente) se obtiene el resultado final D _{τ s} = (3,5 ± 0,1) s . ${\displaystyle {\overline {\eta _{0}\eta _{p}}}}$

Al aumentar s la fluctuación relativa tiende a cero cuando s ^−1/2 . En otras palabras, la relación estadística de la ecuación 82 se vuelve casi cierta para valores grandes de s . Esto permite invertir la relación, es decir, representarla como la dependencia del número promedio de eras s _τ que se intercambian en un intervalo dado τ del tiempo logarítmico doble: ${\displaystyle D_{{\tau }_{s}}/{\overline {\tau _{s}}}}$

La distribución estadística de los valores exactos de s _τ alrededor de su media también es gaussiana con la varianza

${\displaystyle D_{s_{\tau }}=3.5{\frac {{\overline {s_{\tau }}}^{3}}{\tau ^{2}}}=0.26\tau }$

La distribución estadística respectiva está dada por la misma distribución gaussiana en la que la variable aleatoria ahora es s _τ en un τ dado:

Desde este punto de vista, la fuente del comportamiento estadístico es la arbitrariedad en la elección del punto de inicio del intervalo τ superpuesto a la secuencia infinita de las eras intercambiadas.

Con respecto a la densidad de materia, la ecuación 79 se puede reescribir teniendo en cuenta la ecuación 80 en la forma

${\displaystyle \ln \ln {\frac {\varepsilon ^{(s+1)}}{\varepsilon ^{(s)}}}=\eta _{s}+\sum _{p=0}^{s-1}\xi _{p},\quad \eta _{s}=\ln \left[2\delta ^{(s)}\left(k^{(s)}+x^{(s)}-1\right)\Omega ^{(0)}\right]}$

y luego, para el cambio total de energía durante s eras,

El término con la suma por p da la contribución principal a esta expresión porque contiene un exponente con una gran potencia. Dejando solo este término y promediando la ecuación 87 , se obtiene en su lado derecho la expresión que coincide con la ecuación 82 ; todos los demás términos en la suma (también términos con η _s en sus potencias) conducen solo a correcciones de un orden relativo 1/ s . Por lo tanto, ${\displaystyle s{\bar {\xi }}}$

En virtud del carácter casi cierto de la relación entre τ _s y s la ecuación 88 puede escribirse como

${\displaystyle {\overline {\ln \ln \left(\varepsilon _{\tau }/\varepsilon ^{(0)}\right)}}=\tau \quad {\text{or}}\quad {\overline {\ln \ln \left(\varepsilon ^{(s)}/\varepsilon ^{(0)}\right)}}=2.1s,}$

que determina el valor del logaritmo doble del incremento de densidad promediado por intervalos de tiempo doblemente logarítmicos dados τ o por un número dado de eras s .

Estas relaciones estadísticas estables existen específicamente para intervalos de tiempo doblemente logarítmicos y para el aumento de la densidad. Para otras características, por ejemplo, ln (ε ^{( s )} /ε ⁽⁰⁾ ) o Ω ^(s) / Ω ⁽⁰⁾ = exp τ _s, la fluctuación relativa aumenta exponencialmente con el aumento del rango de promedio, lo que anula el significado estable del término valor medio.

El origen de la relación estadística de la ecuación 88 se puede rastrear ya desde la ley inicial que rige la variación de la densidad durante las épocas individuales de Kasner. Según la ecuación 21 , durante toda la evolución tenemos

${\displaystyle \ln \ln \varepsilon (t)={\text{const}}+\ln \Omega +\ln 2(1-p_{3}(t)),}$

con 1 − p ₃ ( t ) cambiando de época en época, recorriendo valores en el intervalo de 0 a 1. El término ln Ω = ln ln (1/ t ) aumenta monótonamente; por otro lado, el término ln2(1 − p ₃ ) puede asumir valores grandes (comparables con ln Ω) solo cuando aparecen valores de p ₃ muy cercanos a la unidad (es decir, muy pequeños | p ₁ |). Estos son precisamente los casos "peligrosos" que perturban el curso regular de la evolución expresado por las relaciones recurrentes eq. 77 – eq. 79 .

Queda por demostrar que tales casos no se dan en realidad en el régimen límite asintótico. La evolución espontánea del modelo comienza en un instante determinado en el que se especifican de manera arbitraria determinadas condiciones iniciales. Por tanto, por "asintótico" se entiende un régimen suficientemente alejado del instante inicial elegido.

Los casos peligrosos son aquellos en los que aparecen valores excesivamente pequeños del parámetro u = x (y por tanto también | p ₁ | ≈ x ) al final de una era. Un criterio para la selección de tales casos es la desigualdad

donde | α ^{( s )} | es la profundidad mínima inicial de las funciones que oscilan en era s (sería más apropiado elegir la amplitud final, pero eso sólo fortalecería el criterio de selección).

El valor de x ⁽⁰⁾ en la primera era está determinado por las condiciones iniciales. Son peligrosos los valores en el intervalo δ x ⁽⁰⁾ ~ exp ( − |α ⁽⁰⁾ | ), y también en intervalos que podrían dar lugar a casos peligrosos en las próximas eras. Para que x ^{( s )} caiga en el intervalo peligroso δ x ^{( s )} ~ exp ( − | α ^{( s )} | ), el valor inicial x ⁽⁰⁾ debe estar en un intervalo de un ancho δ x ⁽⁰⁾ ~ δ x ^{( s )} / k ^{(1)^2} ... k ^{( s )^2} . ^[51] Por lo tanto, a partir de un intervalo unitario de todos los valores posibles de x ⁽⁰⁾ , aparecerán casos peligrosos en partes λ de este intervalo:

(la suma interna se toma sobre todos los valores k ⁽¹⁾ , k ⁽²⁾ , ... , k ^{( s )} desde 1 hasta ∞). Es fácil demostrar que esta era converge al valor λ 1 cuyo orden de magnitud está determinado por el primer término en la ecuación 90 . Esto se puede demostrar mediante una fuerte mayoración de la era para la que se sustituye | α ^{( s )} | = (s + 1) | α ⁽⁰⁾ |, independientemente de las longitudes de las eras k ⁽¹⁾ , k ⁽²⁾ , ... (De hecho | α ^{( s )} | aumenta mucho más rápido; incluso en el caso más desfavorable k ⁽¹⁾ = k ⁽²⁾ = ... = 1 los valores de | α ^{( s )} | aumentan a medida que q ^s | α ⁽⁰⁾ | con q > 1.) Observando que ${\displaystyle \ll }$

${\displaystyle \sum _{k}{\frac {1}{k^{(1)^{2}}k^{(2)^{2}}\dots k^{(s)^{2}}}}=\left(\pi ^{2}/6\right)^{s}}$

uno obtiene

${\displaystyle \lambda =\exp \left(\left|-\alpha ^{(0)}\right|\right)\sum _{s=0}^{\infty }\left[\left(\pi ^{2}/6\right)\exp \left(\left|-\alpha ^{(0)}\right|\right)\right]^{s}\approx \exp \left(\left|-\alpha ^{(0)}\right|\right).}$

Si el valor inicial de x ⁽⁰⁾ se encuentra fuera de la región peligrosa λ no habrá casos peligrosos. Si se encuentra dentro de esta región, se producen casos peligrosos, pero al completarse, el modelo reanuda una evolución "regular" con un nuevo valor inicial que solo ocasionalmente (con una probabilidad λ) puede entrar en el intervalo peligroso. Los casos peligrosos repetidos ocurren con probabilidades λ ² , λ ³ , ... , que convergen asintóticamente a cero.

Solución general con pequeñas oscilaciones

En los modelos anteriores, la evolución de la métrica cerca de la singularidad se estudia en el ejemplo de métricas espaciales homogéneas. De la característica de esta evolución se desprende claramente que la construcción analítica de la solución general para una singularidad de este tipo debe realizarse por separado para cada uno de los componentes básicos de la evolución: para las épocas de Kasner, para el proceso de transición entre épocas causado por "perturbaciones", para eras largas con dos perturbaciones actuando simultáneamente. Durante una época de Kasner (es decir, con pequeñas perturbaciones), la métrica viene dada por la ecuación 7 sin la condición λ = 0.

BKL desarrolló además un modelo independiente de la distribución de la materia (homogéneo o no homogéneo) para eras largas con pequeñas oscilaciones. La dependencia temporal de esta solución resulta ser muy similar a la del caso particular de los modelos homogéneos; este último puede obtenerse a partir del modelo independiente de la distribución mediante una elección especial de las funciones arbitrarias contenidas en él. ^[52]

Es conveniente, sin embargo, construir la solución general en un sistema de coordenadas algo diferente del marco de referencia sincrónico: g _0α = 0 como en el marco sincrónico, pero en lugar de g ₀₀ = 1 ahora es g ₀₀ = − g ₃₃ . Definiendo nuevamente el tensor espacial métrico γ _αβ = − g _αβ se tiene, por lo tanto

La coordenada espacial especial se escribe como x ³ = z y la coordenada temporal se escribe como x ⁰ = ξ (como diferente del tiempo propio t ); se demostrará que ξ corresponde a la misma variable definida en modelos homogéneos. La diferenciación por ξ y z se designa, respectivamente, por punto y prima. Los índices latinos a , b , c toman los valores 1, 2, correspondientes a las coordenadas espaciales x ¹ , x ² que también se escribirán como x , y . Por lo tanto, la métrica es

La solución requerida debe satisfacer las desigualdades

(Estas condiciones especifican que una de las funciones a ² , b ² , c ² es pequeña en comparación con las otras dos, lo que también era el caso con los modelos homogéneos).

La desigualdad ec. 94 significa que los componentes γ _{a 3} son pequeños en el sentido de que en cualquier proporción de los desplazamientos dx ^a y dz , los términos con productos dx ^a dz pueden omitirse en el cuadrado del elemento de longitud espacial dl ² . Por lo tanto, la primera aproximación a una solución es una métrica ec. 92 con γ _{a 3} = 0: ^{[nota 20]}

Se puede convencer fácilmente calculando los componentes del tensor de Ricci , , , utilizando la ecuación métrica 95 y la condición de la ecuación 93 de que todos los términos que contienen derivadas por coordenadas x ^a son pequeños comparados con los términos con derivadas por ξ y z (su razón es ~ γ ₃₃ / γ _ab ). En otras palabras, para obtener las ecuaciones de la aproximación principal, γ ₃₃ y γ _ab en la ecuación 95 deben diferenciarse como si no dependieran de x ^a . Designando ${\displaystyle R_{0}^{0}}$ ${\displaystyle R_{3}^{0}}$ ${\displaystyle R_{3}^{3}}$ ${\displaystyle R_{a}^{b}}$

Se obtienen las siguientes ecuaciones: ^{[nota 21]}

La subida y bajada del índice se realiza aquí con la ayuda de γ _ab . Las cantidades y λ son las contracciones y por lo tanto ${\displaystyle \varkappa }$ ${\displaystyle \varkappa _{a}^{a}}$ ${\displaystyle \lambda _{a}^{a}}$

En cuanto a los componentes del tensor de Ricci , , según este cálculo son idénticamente cero. En la siguiente aproximación (es decir, teniendo en cuenta los pequeños γ _{a 3} y las derivadas por x , y ), determinan las cantidades γ _{a 3} a partir de los ya conocidos γ ₃₃ y γ _ab . ${\displaystyle R_{a}^{0}}$ ${\displaystyle R_{a}^{3}}$

La contracción de la ecuación 97 da , y, por lo tanto, ${\displaystyle G^{\prime \prime }+{\ddot {G}}=0}$

Different cases are possible depending on the G variable. In the above case g⁰⁰ = γ³³ ${\displaystyle \gg }$ γ^ab and ${\displaystyle N\approx g^{00}\left({\dot {G}}\right)^{2}-\gamma ^{33}\left(G^{\prime }\right)^{2}=4\gamma ^{33}{\dot {f}}_{1}{\dot {f}}_{2}}$. The case N > 0 (quantity N is time-like) leads to time singularities of interest. Substituting in eq. 101 f₁ = 1/2 (ξ + z) sin y, f₂ = 1/2 (ξ − z) sin y results in G of type

This choice does not diminish the generality of conclusions; it can be shown that generality is possible (in the first approximation) just on account of the remaining permissible transformations of variables. At N < 0 (quantity N is space-like) one can substitute G = z which generalizes the well-known Einstein–Rosen metric.^[53] At N = 0 one arrives at the Robinson–Bondi wave metric^[54] that depends only on ξ + z or only on ξ − z (cf. ^[55]). The factor sin y in eq. 102 is put for convenient comparison with homogeneous models. Taking into account eq. 102, equations eq. 97 – eq. 99 become

The principal equations are eq. 103 defining the γ_ab components; then, function ψ is found by a simple integration of eq. 104–eq. 105.

The variable ξ runs through the values from 0 to ∞. The solution of eq. 103 is considered at two boundaries, ξ ${\displaystyle \gg }$ 1 and ${\displaystyle \ll }$ 1. At large ξ values, one can look for a solution that takes the form of a 1 / √ξ decomposition:

whereby

(equation 107 needs condition 102 to be true). Substituting eq. 103 in eq. 106, one obtains in the first order

where quantities a^ac constitute a matrix that is inverse to matrix a_ac. The solution of eq. 108 has the form

where l_a, m_a, ρ, are arbitrary functions of coordinates x, y bound by condition eq. 110 derived from eq. 107.

To find higher terms of this decomposition, it is convenient to write the matrix of required quantities γ_ab in the form

where the symbol ~ means matrix transposition. Matrix H is symmetric and its trace is zero. Presentation eq. 111 ensures symmetry of γ_ab and fulfillment of condition eq. 102. If exp H is substituted with 1, one obtains from eq. 111 γ_ab = ξa_ab with a_ab from eq. 109. In other words, the first term of γ_ab decomposition corresponds to H = 0; higher terms are obtained by powers decomposition of matrix H whose components are considered small.

The independent components of matrix H are written as σ and φ so that

Substituting eq. 111 in eq. 103 and leaving only terms linear by H, one derives for σ and φ

${\displaystyle {\ddot {\sigma }}+\xi ^{-1}{\dot {\sigma }}-\sigma ^{\prime \prime }=0,}$

If one tries to find a solution to these equations as Fourier series by the z coordinate, then for the series coefficients, as functions of ξ, one obtains Bessel equations. The major asymptotic terms of the solution at large ξ are^{[note 22]}

${\displaystyle \sigma ={\frac {1}{\sqrt {\xi }}}\sum _{n=-\infty }^{\infty }\left(A_{1n}e^{in\omega \xi }+B_{1n}e^{-in\omega \xi }\right)e^{in\omega z},}$

${\displaystyle \omega _{n}^{2}=n^{2}\omega ^{2}+4\rho ^{2}.}$

Coefficients A and B are arbitrary complex functions of coordinates x, y and satisfy the necessary conditions for real σ and φ; the base frequency ω is an arbitrary real function of x, y. Now from eq. 104–eq. 105 it is easy to obtain the first term of the function ψ:

(this term vanishes if ρ = 0; in this case the major term is the one linear for ξ from the decomposition: ψ = ξq (x, y) where q is a positive function^[56]).

Therefore, at large ξ values, the components of the metric tensor γ_ab oscillate upon decreasing ξ on the background of a slow decrease caused by the decreasing ξ factor in eq. 111. The component γ₃₃ = e^ψ decreases quickly by a law close to exp (ρ²ξ²); this makes it possible for condition eq. 93.^{[note 23]}

Next BKL consider the case ξ ${\displaystyle \ll }$ 1. The first approximation to a solution of eq. 103 is found by the assumption (confirmed by the result) that in these equations terms with derivatives by coordinates can be left out:

This equation together with the condition eq. 102 gives

where λ_a, μ_a, s₁, s₂ are arbitrary functions of all 3 coordinates x, y, z, which are related with other conditions

Equations eq. 104–eq. 105 give now

The derivatives ${\displaystyle {\lambda _{a}^{b}}^{\prime }}$, calculated by eq. 118, contain terms ~ ξ^{4s₁ − 2} and ~ ξ^{4s₂ − 2} while terms left in eq. 117 are ~ ξ⁻². Therefore, application of eq. 103 instead of eq. 117 is permitted on conditions s₁ > 0, s₂ > 0; hence 1 − ${\displaystyle s_{1}^{2}-s_{2}^{2}}$ > 0.

Thus, at small ξ oscillations of functions γ_ab cease while function γ₃₃ begins to increase at decreasing ξ. This is a Kasner mode and when γ₃₃ is compared to γ_ab, the above approximation is not applicable.

In order to check the compatibility of this analysis, BKL studied the equations ${\displaystyle R_{\alpha }^{0}}$ = 0, ${\displaystyle R_{\alpha }^{3}}$ = 0, and, calculating from them the components γ_a3, confirmed that the inequality eq. 94 takes place. This study^[52] showed that in both asymptotic regions the components γ_a3 were ~ γ₃₃. Therefore, correctness of inequality eq. 93 immediately implies correctness of inequality eq. 94.

This solution contains, as it should for the general case of a field in vacuum, four arbitrary functions of the three space coordinates x, y, z. In the region ξ ${\displaystyle \ll }$ 1 these functions are, e.g., λ₁, λ₂, μ₁, s₁. In the region ξ ${\displaystyle \gg }$ 1 the four functions are defined by the Fourier series by coordinate z from eq. 115 with coefficients that are functions of x, y; although Fourier series decomposition (or integral?) characterizes a special class of functions, this class is large enough to encompass any finite subset of the set of all possible initial conditions.

The solution contains also a number of other arbitrary functions of the coordinates x, y. Such two-dimensional arbitrary functions appear, generally speaking, because the relationships between three-dimensional functions in the solutions of the Einstein equations are differential (and not algebraic), leaving aside the deeper problem about the geometric meaning of these functions. BKL did not calculate the number of independent two-dimensional functions because in this case it is hard to make unambiguous conclusions since the three-dimensional functions are defined by a set of two-dimensional functions (cf.^[52] for more details).^{[note 24]}

Finally, BKL go on to show that the general solution contains the particular solution obtained above for homogeneous models.

Substituting the basis vectors for Bianchi Type IX homogeneous space in eq. 7 the space-time metric of this model takes the form

When c² ${\displaystyle \ll }$ a², b², one can ignore c² everywhere except in the term c² dz². To move from the synchronous frame used in eq. 121 to a frame with conditions eq. 91, the transformation dt = c dξ/2 and substitution z → z/2 are done. Assuming also that χ ≡ ln (a/b) ${\displaystyle \ll }$ 1, one obtains from eq. 121 in the first approximation:

Similarly, with the basis vectors of Bianchi Type VIII homogeneous space, one obtains

According to the analysis of homogeneous spaces above, in both cases ab = ξ (simplifying ${\displaystyle a_{0}^{2}}$ = ξ₀) and χ is from eq. 51; function c (ξ) is given by formulae eq. 53 and eq. 61, respectively, for models of Types IX and VIII.

Identical metric for Type VIII is obtained from eq. 112, eq. 115, eq. 116 choosing two-dimensional vectors l_a and m_a in the form

and substituting

To obtain the metric for Type IX, one should substitute

(for calculation of c (ξ) the approximation in eq. 116 is not sufficient and the term in ψ linear by ξ is calculated^[56])

This analysis was done for empty space. Including matter does not make the solution less general and does not change its qualitative characteristics.^[56][52]

A limitation of great importance for the general solution is that all 3-dimensional functions contained in the metrics eq. 122 and eq. 123 should have a single and common characteristic change interval. Only this allows to approximate in the Einstein equations all metric spatial component derivatives with simple products of these components by a characteristic wave numbers which results in ordinary differential equations of the type obtained for the Type IX homogeneous model. This is the reason for the coincidence between homogeneous and general solutions.

It follows that both Type IX model and its generalisation contain an oscillatory mode with a single spatial scale of an arbitrary magnitude which is not selected among others by any physical conditions. However, it is known that in non-linear systems with infinite degrees of freedom such mode is unstable and partially dissipates to smaller oscillations. In the general case of small perturbations with an arbitrary spectrum, there will always be some whose amplitudes will increase feeding upon the total process energy. As a result, a complicated picture arises of multi-scale movements with certain energy distribution and energy exchange between oscillations of different scales. It doesn't occur only in the case when the development of small-scale oscillations is impossible because of physical conditions. For the latter, some natural physical length must exist which determines the minimal scale at which energy exits from a system with dynamical degrees of freedom (which, for example, occurs in a liquid with a certain viscosity). However, there is no innate physical scale for a gravitational field in vacuum, and, therefore, there is no impediment for the development of oscillations of arbitrarily small scales.^[57]

Conclusions

BKL describe singularities in the cosmologic solution of Einstein equations that have a complicated oscillatory character. Although these singularities have been studied primarily on spatially homogeneous models, there are convincing reasons to assume that singularities in the general solution of Einstein equations have the same characteristics; this circumstance makes the BKL model important for cosmology.

A basis for such statement is the fact that the oscillatory mode in the approach to singularity is caused by the single perturbation that also causes instability in the generalized Kasner solution. A confirmation of the generality of the model is the analytic construction for long era with small oscillations. Although this latter behavior is not a necessary element of metric evolution close to the singularity, it has all principal qualitative properties: metric oscillation in two spatial dimensions and monotonous change in the third dimension with a certain perturbation of this mode at the end of some time interval. However, the transitions between Kasner epochs in the general case of non-homogeneous spatial metric have not been elucidated in details.

The problem connected with the possible limitations upon space geometry caused by the singularity was left aside for further study. It is clear from the outset, however, that the original BKL model is applicable to both finite or infinite space; this is evidenced by the existence of oscillatory singularity models for both closed and open spacetimes.

The oscillatory mode of the approach to singularity gives a new aspect to the term 'finiteness of time'. Between any finite moment of the world time t and the moment t = 0 there is an infinite number of oscillations. In this sense, the process acquires an infinite character. Instead of time t, a more adequate variable for its description is ln t by which the process is extended to ${\displaystyle -\infty }$.

BKL consider metric evolution in the direction of decreasing time. The Einstein equations are symmetric in respect to the time sign so that a metric evolution in the direction of increasing time is equally possible. However, these two cases are fundamentally different because past and future are not equivalent in the physical sense. Future singularity can be physically meaningful only if it is possible at arbitrary initial conditions existing in a previous moment. Matter distribution and fields in some moment in the evolution of Universe do not necessarily correspond to the specific conditions required for the existence of a given special solution to the Einstein equations.

The choice of solutions corresponding to the real world is related to profound physical requirements which is impossible to find using only the existing relativity theory and which can be found as a result of future synthesis of physical theories. Thus, it may turn out that this choice singles out some special (e.g., isotropic) type of singularity. Nevertheless, it is more natural to assume that because of its general character, the oscillatory mode should be the main characteristic of the initial evolutionary stages.

In this respect, of considerable interest is the property of the "Mixmaster" model shown by Misner,^[58] related to propagation of light signals. In the isotropic model, a "light horizon" exists, meaning that for each moment of time, there is some longest distance, at which exchange of light signals and, thus, a causal connection, is impossible: the signal cannot reach such distances for the time since the singularity t = 0.

Signal propagation is determined by the equation ds = 0. In the isotropic model near the singularity t = 0 the interval element is ${\displaystyle ds^{2}=dt^{2}-2td{\bar {l}}^{2}}$, where ${\displaystyle d{\bar {l}}^{2}}$ is a time-independent spatial differential form.^[59] Substituting ${\displaystyle t=\eta ^{2}/2}$ yields

The "distance" ${\displaystyle \Delta {\bar {l}}}$ reached by the signal is

Since η, like t, runs through values starting from 0, up to the "moment" η signals can propagate only at the distance ${\displaystyle \Delta {\bar {l}}\leq \eta }$ which fixes the farthest distance to the horizon.

The existence of a light horizon in the isotropic model poses a problem in the understanding of the origin of the presently observed isotropy in the relic radiation. According to the isotropic model, the observed isotropy means isotropic properties of radiation that comes to the observer from such regions of space that can not be causally connected with each other. The situation in the oscillatory evolution model near the singularity can be different.

For example, in the homogeneous model for Type IX space, a signal is propagated in a direction in which for a long era, scales change by a law close to ~ t. The square of the distance element in this direction is dl² = t² ${\displaystyle {\bar {l}}^{2}}$, and the respective element of the four-dimensional interval is ${\displaystyle ds^{2}=dt^{2}-t^{2}{\bar {l}}^{2}}$. The substitution ${\displaystyle t=e^{\eta }}$ puts this in the form

and for the signal propagation one has equation of the type eq. 128 again. The important difference is that the variable η runs now through values starting from ${\displaystyle -\infty }$ (if metric eq. 129 is valid for all t starting from t = 0).

Therefore, for each given "moment" η are found intermediate intervals Δη sufficient for the signal to cover each finite distance.

In this way, during a long era a light horizon is opened in a given space direction. Although the duration of each long era is still finite, during the course of the world evolution eras change an infinite number of times in different space directions. This circumstance makes one expect that in this model a causal connection between events in the whole space is possible. Because of this property, Misner named this model "Mixmaster universe" by a brand name of a dough-blending machine.

As time passes and one goes away from the singularity, the effect of matter on metric evolution, which was insignificant at the early stages of evolution, gradually increases and eventually becomes dominant. It can be expected that this effect will lead to a gradual "isotropisation" of space as a result of which its characteristics come closer to the Friedman model which adequately describes the present state of the Universe.

Finally, BKL pose the problem about the feasibility of considering a "singular state" of a world with infinitely dense matter on the basis of the existing relativity theory. The physical application of the Einstein equations in their present form in these conditions can be made clear only in the process of a future synthesis of physical theories and in this sense the problem can not be solved at present.

It is important that the gravitational theory itself does not lose its logical cohesion (i.e., does not lead to internal controversies) at whatever matter densities. In other words, this theory is not limited by the conditions that it imposes, which could make logically inadmissible and controversial its application at very large densities; limitations could, in principle, appear only as a result of factors that are "external" to the gravitational theory. This circumstance makes the study of singularities in cosmological models formally acceptable and necessary in the frame of existing theory.

Notes

1. A similar animated simulation by David Garfinkle can be found in.^[1]
2. The convention used by BKL is the same as in the Landau & Lifshitz (1988) book. The Latin indices run through the values 0, 1, 2, 3; Greek indices run through the space values 1, 2, 3. The metric g_ik has the signature (+ − − −); γ_αβ = −g_αβ is the 3-dimensional space metric tensor. BKL use a system of units, in which the speed of light and the Einstein gravitational constant are equal to 1.
3. The expression for r is derived by logarithming the power coefficients in the metric: ln [t^2p_α(1/u)] = 2p_α(1/u) ln t.
4. When (p₁, p₂, p₃) = (0, 0, 1) the spacetime metric eq. 1 with dl² from eq. 2 transforms to Galilean metric with the substitution t sh z = ζ, t ch z = τ, that is, the singularity is fictional and the spacetime is flat.
5. Here and below all symbols for vector operations (vector products, the operations rot, grad, etc.) should be understood in a very formal way as operations over the covariant components of the vectors l, m, n such that are performed in Cartesian coordinates x¹, x², x³.
6. Excepting the case (p₁, p₂, p₃) = (0, 0, 1), in which the metric singularity is fictitious.
7. The constants λ, μ, ν are the so-called structural constants of the space movement group.
8. In their exact form, the Einstein equations for homogeneous space contain, in general, 6 different functions of time γ_ab(t) in the metric. The fact that in the present case a consistent system of exact equations is obtained for the metric which contains only 3 functions of time (γ₁₁ = а², γ₂₂ = b², γ₃₃ = c²) is related to a symmetry that leads to the disappearance of 6 Ricci tensor components.
9. The asymptotic values of α_τ, β_τ, γ_τ at τ → −∞ can be found without fully solving eq. 29. It suffices to note that the first of these equations has a form of a "particle" moving in one dimension in the field of an exponential potential wall with α playing the role of a constant. In this analogy, the Kasner mode refers to a free movement with constant velocity α_τ = Λp₁. After reflection from the wall, the particle moves freely with velocity α_τ = −Λp₁. Also noting that from eq. 29 α_τ + β_τ = const, and α_τ + γ_τ = const, one can see that β_τ and γ_τ take the values β_τ = Λ(p₂ − 2p₁), γ_τ = Λ(p₃ − 2p₁).
10. Introduction of non-diagonal components of γ_ab(t) imparts some new features to the BKL model: rotations of axes corresponding to the Kasner epoch powers; this problem is studied in Belinsky, Khalatnikov & Lifshitz (1971)
11. The constant in the sine argument, of course, is not necessarily the same as ξ₀ in eq. 47 and eq. 48; however, making them the same does not change in any way the solution character.
12. In a more precise calculation, a slowly changing logarithmic term appears in the sine argument, and a multiplier appears in front the exponent in the expression for с(ξ), see Belinsky, Khalatnikov & Lifshitz 1970, Appendix B.
13. If in eq. 49, one substitutes sh 2χ with 2χ and solves it for all values of ξ, one obtains χ = c₁J₀(ξ) + c₂N₀(ξ) where J₀, N₀ are Bessel functions of the I and II kind. This solution interpolates between the two limiting cases and allows to relate by an order of magnitude the constant parameters in eq. 52 and eq. 55.
14. Since a, b, c have the dimension of length, their logarithms are defined only up to an additive constant which depends on the choice of the length units; in this sense eq. 63 has a conditional meaning corresponding to a certain choice of the zero value of α, β, γ.
15. According to eq. 32, transitions are large with small |p₁| (i. e. large u) and are ≈1/|p₁| ~ u. But even in this case Δ_n ~ u_n |α_n| ${\displaystyle \gg }$ u_n
16. Fixing the limits of the era according to eq. 64 is meaningful because in such case the era contains all epochs in which the third function, γ(t) decreases monotonously. If the era is defined by the sequence of u values from k + x to 1 + x, then the monotonous decrease of γ(t) will continue during the first epoch of the next era.
17. Epoch lengths are great in comparison to transitions between epochs. According to eq. 33 transition lengths are great at small |p₁| (i.e. large u) and are ∝ 1/|p₁| ∝ u. But even in this case Δ_n ∝ u_n|α_n| ${\displaystyle \gg }$ u_n.
18. Equation 74 was known already to Gauss, and an equation of type eq. 73c was considered in this connection by Rodion Kuzmin (see Gauss–Kuzmin distribution). Further information on the chaotic behaviour and entropy of continued fractions in Linas Vepstas. 2008. Entropy of Continued Fractions (Gauss-Kuzmin Entropy)
19. The plot of the function P(δ) in Fig. 2 in Lifshitz, Lifshitz & Khalatnikov 1970 is incorrect for several reasons. Apparently some errors were admitted in preparing the program for numerical solution of the integral equation. Also a "forced" reduction of the values P(0) and P(1) was performed in view of the incorrect footnote in Lifshitz, Lifshitz & Khalatnikov 1970, Sec. 4. The finite probability of the value δ = 0 does not mean the possibility of the initial amplitude of oscillation becoming zero (which would be in contradiction to the regular course of evolution shown in Fig. 4). From eq. 78 δ_s+1 tends to zero with x_s → 0 proportional to x_s; but the amplitude is given by the product δ_s+1Ω_s+1, which tends to a finite limit since the expression eq. 77 contains a term with 1/x_s.
20. Note that this metric allows arbitrary transformations of type ξ′ + z″ = f₁ (ξ + z), ξ′ − z′ = f₂ (ξ − z), x′^a = f^a (x¹, x²).
21. The equation ${\displaystyle R_{0}^{0}+R_{3}^{3}=0}$ is a direct result of eq. 97–eq. 99 if ${\displaystyle {\dot {G}}\neq 0}$ or ${\displaystyle G^{\prime }\neq 0}$. The case ${\displaystyle {\dot {G}}=G^{\prime }=0}$ does not require a special treatment: it can be shown that the spacetime metric in this case converges (in first approximation) to Galilean.
22. It is possible to look for a solution in the form of Fourier integrals; this issue has not been studied in detail. Therefore, BKL do not require Fourier series decomposition as a mandatory condition for the coordinate dependence of functions σ and φ
23. Squared H terms in eq. 103 result only in small (≈1/ξ) corrections in σ and φ. Calculation with cubic terms leads to appearance of a weak dependence of A, B from ξ that can be presented as an appearance of logarithmic phases in the oscillating factors in eq. 115. These calculations for the case ρ = 0 are given in Belinsky & Khalatnikov (1970, Appendix B) (cf. the analogous situation for homogeneous models, Belinsky, Khalatnikov & Lifshitz (1970, Appendix B)).
24. The regular decomposition of the general solution of Einstein equations contains (in addition to the four three-dimensional functions) three independent functions of two coordinates (cf. Petrov 1969, Ch. 40; Lifshitz & Khalatnikov (1963, Appendix A))

References

1. Garfinkle, David (2007). "Of singularities and breadmaking". Einstein Online. Band 03. Max Planck Institute for Gravitational Physics. 03–1014. Retrieved 2020-10-15.
2. Belinsky, Khalatnikov & Lifshitz 1970
3. Demaret, Henneaux & Spindel 1985.
4. Demaret et al. 1986.
5. Demaret, de Rop & Henneaux 1989.
6. Damour & Henneaux 2000.
7. Damour et al. 2001.
8. Damour, Henneaux & Nicolai 2003.
9. Kac 1983.
10. Damour 2015.
11. Henneaux, Persson & Spindel 2008.
12. Lifshitz & Khalatnikov 1963
13. Landau & Lifshitz 1988, Ch. 97
14. Lifshitz & Khalatnikov 1961a.
15. Lifshitz & Khalatnikov 1961b.
16. Lifshitz, Sudakov & Khalatnikov 1961
17. Hawking 1965.
18. Hawking & Ellis 1968.
19. Geroch 1966.
20. Ashtekar, Henderson & Sloan 2011
21. Barrow & Tipler 1979.
22. Barrow & Tipler 1981.
23. Berger 2002
24. Garfinkle 2004.
25. Berger & Moncrief 1993.
26. Berger et al. 1998.
27. Weaver, Isenberg & Berger 1998.
28. Andersson & Rendall 2001.
29. Damour et al. 2002.
30. Berger & Moncrief 1998.
31. Berger & Moncrief 2000.
32. Garfinkle 2007.
33. Saotome, Akhoury & Garfinkle 2010.
34. Kasner 1921.
35. Rugh 1994.
36. Bini, Cherubini & Jantzen 2007.
37. Landau & Lifshitz 1988, Ch. 117, Problem 3.
38. Landau & Lifshitz 1987, Ch. 134, eq. 134.15.
39. Misner, Thorne & Wheeler 1973, p. 564.
40. Nelson 1981.
41. Belinsky & Khalatnikov 1966.
42. Khalatnikov & Lifshitz 1970.
43. Belinsky & Khalatnikov 1969a
44. Lifshitz & Khalatnikov 1970
45. Belinsky, Khalatnikov & Lifshitz 1970, Appendix C.
46. Lifshitz & Khalatnikov 1963, Appendix C.
47. Taub 1951.
48. Lifshitz, Lifshitz & Khalatnikov 1970
49. Khalatnikov et al. 1985
50. Chernoff & Barrow 1983.
51. Belinsky, Khalatnikov & Lifshitz 1970, Appendix A.
52. Belinsky & Khalatnikov 1970
53. Einstein & Rosen 1937.
54. Bondi, Pirani & Robinson 1959.
55. Landau & Lifshitz 1988, Ch. 109.
56. Belinsky & Khalatnikov 1969b
57. Belinsky 1992.
58. Misner 1969.
59. Landau & Lifshitz 1988, Ch. 103–105.

Bibliography

• Andersson, Lars; Rendall, Alan D. (2001). "Quiescent cosmological singularities". Communications in Mathematical Physics. 218 (3): 479–511. arXiv:gr-qc/0001047. Bibcode:2001CMaPh.218..479A. doi:10.1007/s002200100406. S2CID 16167683.
• Ashtekar, Abhay; Henderson, Adam; Sloan, David (2011). "Hamiltonian formulation of the Belinskii-Khalatnikov-Lifshitz conjecture". Physical Review D. 83 (8): 084024. arXiv:1102.3474. Bibcode:2011PhRvD..83h4024A. doi:10.1103/PhysRevD.83.084024. S2CID 119888235.
• Barrow, John D.; Tipler, Frank J. (1979). "Analysis of the generic singularity studies by Belinskii, Khalatnikov, and Lifshitz". Physics Reports. 56 (7): 371–402. Bibcode:1979PhR....56..371B. doi:10.1016/0370-1573(79)90097-8.
• Barrow, John D.; Tipler, Frank J. (1981). "Generic singularity studies revisited". Physics Letters. 82A (9): 441–445. doi:10.1016/B978-0-08-036364-6.50050-8.
• Belinsky, Vladimir A.; Khalatnikov, I.M. (1966). "A general solution of the gravitational equations with a simultaneous fictitious singularity". JETP. 49 (3): 1000. Bibcode:1966JETP...22..694B.
• Belinsky, Vladimir A.; Khalatnikov, I.M. (1969a). "On the nature of the singularities in the general solution of the gravitational equations". JETP. 56: 1700.
• Belinsky, Vladimir A.; Khalatnikov, I.M. (1969b). "General solution of the gravitational equations with a physical singularity". JETP. 57: 2163.
• Belinsky, Vladimir A.; Khalatnikov, Isaak M.; Lifshitz, Evgeny M. (1970). "Колебательный режим приближения к особой точке в релятивистской космологии". Uspekhi Fizicheskikh Nauk. 102 (11): 463–500. Bibcode:1970UsFiN.102..463B. doi:10.3367/ufnr.0102.197011d.0463.; English translation in Belinskii, V.A.; Khalatnikov, I.M.; Lifshitz, E.M. (1970). "Oscillatory Approach to a Singular Point in the Relativistic Cosmology". Advances in Physics. 19 (80): 525–573. Bibcode:1970AdPhy..19..525B. doi:10.1080/00018737000101171.
• Belinsky, Vladimir A.; Khalatnikov, Isaak M. (1970). "General solution of the gravitational equations with a physical oscillatory singularity". JETP. 59: 314. Bibcode:1971JETP...32..169B.
• Belinsky, Vladimir A.; Khalatnikov, I.M.; Lifshitz, E.M. (1971). "The oscillatory mode of approach to a singularity in homogeneous cosmological models with rotating axes". JETP. 60 (6): 1969–1979.
• Belinsky, V.A. (1992). "Turbulence of a Gravitational Field near a Cosmological Singularity". JETP Letters. 56 (9): 437–440.
• Belinski, Vladimir; Henneaux, Marc (2018). The Cosmological Singularity. Cambridge University Press. arXiv:1404.3864. Bibcode:2018cosm.book.....B. doi:10.1017/9781107239333. ISBN 978-1-107-04747-1.
• Berger, Beverly; Moncrief, Vincent (1993). "Numerical investigation of cosmological singularities". Physical Review D. 48 (10): 4676–4687. arXiv:gr-qc/9307032. Bibcode:1993PhRvD..48.4676B. doi:10.1103/PhysRevD.48.4676. PMID 10016121. S2CID 450414.
• Berger, Beverly K.; Moncrief, Vincent (1998). "Numerical evidence that the singularity in polarized U(1) symmetric cosmologies on T³ × R is velocity dominated". Physical Review D. 57 (12): 7235–7240. arXiv:gr-qc/9801078. Bibcode:1998PhRvD..57.7235B. doi:10.1103/PhysRevD.57.7235. S2CID 119539705.
• Berger, Beverly; Garfinkle, David; Isenberg, James; Moncrief, Vincent; Weaver, Marsha (1998). "The singularity in generic gravitational collapse is spacelike, local, and oscillatory". Modern Physics Letters A. 13 (19): 1565–1573. arXiv:gr-qc/9805063. Bibcode:1998MPLA...13.1565B. doi:10.1142/S0217732398001649. S2CID 118889710.
• Berger, Beverly K.; Moncrief, Vincent (2000). "Signature for local Mixmaster dynamics in U(1) symmetric cosmologies". Physical Review D. 62 (123501): 123501. arXiv:gr-qc/0006071. Bibcode:2000PhRvD..62l3501B. doi:10.1103/PhysRevD.62.123501. S2CID 10389665.
• Berger, Beverly K (2002). "Numerical Approaches to Spacetime Singularities". Living Reviews in Relativity. 5 (1): 1. arXiv:gr-qc/0201056. Bibcode:2002LRR.....5....1B. doi:10.12942/lrr-2002-1. PMC 5256073. PMID 28179859.
• Bini, Donato; Cherubini, Christian; Jantzen, Robert (2007). "The Lifshitz-Khalatnikov Kasner index parametrization and the Weyl tensor". Il Nuovo Cimento B. 122 (5): 521–536. arXiv:0710.4902. Bibcode:2007NCimB.122..521B. doi:10.1393/ncb/i2007-10396-4. S2CID 15854390.
• Bini, Donato; Cherubini, Christian; Geralico, Andrea; Jantzen, Robert T. (2009). "Electrocardiogram of the Mixmaster Universe". Classical and Quantum Gravity. 26 (2): 025012. arXiv:0808.0828. Bibcode:2009CQGra..26b5012B. doi:10.1088/0264-9381/26/2/025012. S2CID 14552653.
• Bondi, Herman; Pirani, F.A.E.; Robinson, I. (1959). "Gravitational Waves in General Relativity. III. Exact Plane Waves". Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences. 251 (1267): 519–533. Bibcode:1959RSPSA.251..519B. doi:10.1098/rspa.1959.0124. JSTOR 100727. S2CID 122766998.
• Chernoff, David F.; Barrow, J.D. (1983). "Chaos in the Mixmaster Universe". Physical Review Letters. 50 (2): 134–137. Bibcode:1983PhRvL..50..134C. doi:10.1103/PhysRevLett.50.134.
• Damour, Thibault; Henneaux, Marc (2000). "Chaos in superstring cosmology". Physical Review Letters. 85 (5): 920–923. arXiv:hep-th/0003139. Bibcode:2000PhRvL..85..920D. doi:10.1103/PhysRevLett.85.920. PMID 10991439. S2CID 10752273.
• Damour, Thibault; Henneaux, Marc; Julia, Bernard; Nicolai, Hermann (2001). "Hyperbolic Kac–Moody algebras and chaos in Kaluza-Klein models". Physics Letters B. 509 (3–4): 323–330. arXiv:hep-th/0103094. Bibcode:2001PhLB..509..323D. doi:10.1016/S0370-2693(01)00498-1. S2CID 16964946.
• Damour, Thibault; Henneaux, Marc; Nicolai, Hermann (2003). "Cosmological billiards". Classical and Quantum Gravity. 20 (9): R145–R200. CiteSeerX 10.1.1.262.7733. doi:10.1088/0264-9381/20/9/201. S2CID 250877925.
• Damour, Thibault; Henneaux, Marc; Rendall, Alan D.; Weaver, Marsha (2002). "Kasner-like behaviour for subcritical Einstein-matter systems". Annales Henri Poincaré. 3 (6): 1049–1111. arXiv:gr-qc/0202069. Bibcode:2002AnHP....3.1049D. doi:10.1007/s000230200000. S2CID 17092394.
• Demaret, Jacques; Henneaux, Marc; Spindel, Philipe (1985). "Non-oscillatory behaviour in vacuum Kaluza–Klein cosmologies". Physics Letters. 164B (1–3): 27–29. Bibcode:1985PhLB..164...27D. doi:10.1016/0370-2693(85)90024-3.
• Demaret, Jacques; Hanquin, Jean-Luc; Henneaux, Marc; Spindel, Philipe; Taormina, Anna (1986). "The fate of the Mixmaster behaviour in vacuum inhomogeneous Kaluza-Klein cosmological models". Physics Letters B. 175 (2): 129–132. Bibcode:1986PhLB..175..129D. doi:10.1016/0370-2693(86)90701-X.
• Demaret, Jacques; de Rop, Yves; Henneaux, Marc (1989). "Are Kaluza-Klein models of the Universe chaotic?". International Journal of Theoretical Physics. 28 (9): 1067–1079. Bibcode:1989IJTP...28.1067D. doi:10.1007/BF00670349. S2CID 121065247.
• Einstein, Albert; Rosen, Nathan (1937). "On gravitational waves". Journal of the Franklin Institute. 223 (1): 43–54. Bibcode:1937FrInJ.223...43E. doi:10.1016/S0016-0032(37)90583-0.
• Frasca, Marco (2006). "Strong coupling expansion for general relativity". International Journal of Modern Physics D. 15 (9): 1373–1386. arXiv:hep-th/0508246. Bibcode:2006IJMPD..15.1373F. doi:10.1142/S0218271806009091. S2CID 15369171.
• Garfinkle, David (2004). "Numerical Simulations of Generic Singularities". Phys. Rev. Lett. 93 (16): 161101. arXiv:gr-qc/0312117. Bibcode:2004PhRvL..93p1101G. doi:10.1103/PhysRevLett.93.161101. PMID 15524970. S2CID 37917240.
• Garfinkle, David (2007). "Numerical simulations of general gravitational singularities". Classical and Quantum Gravity. 24 (12): 295–306. arXiv:0808.0160. Bibcode:2007CQGra..24S.295G. doi:10.1088/0264-9381/24/12/S19. S2CID 16899122.
• Geroch, Robert P. (1966). "Singularities in Closed Universes". Physical Review Letters. 17 (8): 445–447. Bibcode:1966PhRvL..17..445G. doi:10.1103/PhysRevLett.17.445.
• Góźdź, Andrzej; Pędrak, Aleksandra; Piechocki, Włodzimierz (2023). "Quantum dynamics corresponding to the chaotic BKL scenario". The European Physical Journal C. 83 (2): 150. arXiv:2204.11274. Bibcode:2023EPJC...83..150G. doi:10.1140/epjc/s10052-023-11284-6. S2CID 254044770.
• Hawking, Stephen W. (1965). "Occurrence of Singularities in Open Universes". Physical Review Letters. 15 (17): 689–690. Bibcode:1965PhRvL..15..689H. doi:10.1103/PhysRevLett.15.689.
• Hawking, Stephen W.; Ellis, G.F.R. (1968). "The Cosmic Black-Body Radiation and the Existence of Singularities in Our Universe". Astrophysical Journal. 152: 25. Bibcode:1968ApJ...152...25H. doi:10.1086/149520.
• Heinzle, J. Mark; Uggla, Claes; Röhr, Niklas (2009). "The cosmological billiard attractor". Adv. Theor. Math. Phys. 13 (2): 293–407. arXiv:gr-qc/0702141. Bibcode:2007gr.qc.....2141H. doi:10.4310/ATMP.2009.v13.n2.a1. S2CID 119470976.
• Henneaux, Marc; Persson, Daniel; Spindel, Philippe (2008). "Spacelike Singularities and Hidden Symmetries of Gravity". Living Reviews in Relativity. 11 (1): 1. arXiv:0710.1818. Bibcode:2008LRR....11....1H. doi:10.12942/lrr-2008-1. PMC 5255974. PMID 28179821.
• Kac, Victor G. (1983). Infinite dimensional Lie algebras: an introduction. Progress in Mathematics. Vol. 44. Basel: Birkhäuser. p. 245. doi:10.1007/978-1-4757-1382-4. ISBN 9780817631185.
• Kasner, Edward (1921). "Geometrical Theorems on Einstein's Cosmological Equations". American Journal of Mathematics. 43 (4): 217–221. Bibcode:1921AmJM...43..217K. doi:10.2307/2370192. JSTOR 2370192.
• Khalatnikov, Isaak M.; Lifshitz, E.M.; Khanin, K.M.; Shchur, L.N.; Sinai, Ya.G. (1985). "On the stochasticity in relativistic cosmology". Journal of Statistical Physics. 38 (1–2): 97–114. Bibcode:1985JSP....38...97K. doi:10.1007/BF01017851. S2CID 120521834.
• Khalatnikov, Isaak M.; Kamenshchik, Aleksander Yu. (2008). "Lev Landau and the problem of singularities in cosmology". Physics-Uspekhi. 51 (6): 609–616. arXiv:0803.2684. Bibcode:2008PhyU...51..609K. doi:10.1070/PU2008v051n06ABEH006550. S2CID 14878079.
• Khalatnikov, I.M.; Lifshitz, E.M. (1970). "General Cosmological Solution of the Gravitational Equations with a Singularity in Time". Physical Review Letters. 24 (2): 76. Bibcode:1970PhRvL..24...76K. doi:10.1103/PhysRevLett.24.76.
• Landau, Lev D.; Lifshitz, Evgeny M. (1988). Classical Theory of Fields. Course of Theoretical Physics. Vol. 2 (7th ed.). Moscow: Nauka. ISBN 978-5-02-014420-0.
• Landau, Lev D.; Lifshitz, Evgeny M. (1987). Fluid Mechanics. Course of Theoretical Physics. Vol. 6 (2nd ed.). Butterworth-Heinemann. ISBN 978-0-08-033933-7.
• Lifshitz, Evgeny M.; I.M. Khalatnikov (1961). "On the singularities of cosmological solutions of the gravitational equations.I". JETP. 39: 149.
• Lifshitz, Evgeny M.; I.M. Khalatnikov (1961). "On the singularities of cosmological solutions of the gravitational equations.II". JETP. 39: 800.
• Lifshitz, Evgeny M.; Sudakov, V.V.; Khalatnikov, I.M. (1961). "Singularities of cosmological solutions of the gravitational equations.III". JETP. 40: 1847.; Physical Review Letters, 6, 311 (1961)
• Lifshitz, Evgeny M.; Khalatnikov, Isaak M. (1963). "Проблемы релятивистской космологии". Uspekhi Fizicheskikh Nauk. 80 (7): 391–438. doi:10.3367/UFNr.0080.196307d.0391.; English translation in Lifshitz, E.M.; Khalatnikov, I.M. (1963). "Problems in the Relativistic Cosmology". Advances in Physics. 12 (46): 185. Bibcode:1963AdPhy..12..185L. doi:10.1080/00018736300101283.
• Lifshitz, Evgeny M.; Khalatnikov, Isaak M. (1970). "Oscillatory mode of approach to a singularity in the open cosmological model". JETP Letters. 11: 200–203.
• Lifshitz, E.M.; Lifshitz, I.M.; Khalatnikov, I.M. (1970). "Asymptotic analysis of oscillatory mode of approach to a singularity in homogeneous cosmological models". JETP. 59: 322.
• Misner, Ch. W. (1969). "Mixmaster Universe". Physical Review Letters. 22 (20): 1071–1074. Bibcode:1969PhRvL..22.1071M. doi:10.1103/PhysRevLett.22.1071.
• Misner, Charles W.; Thorne, Kip S.; Wheeler, John Archibald (1973). Gravitation. San Francisco: W.H. Freeman. ISBN 978-0-7167-0334-1.^{[dead link]}
• Nelson, Robert A. (1981). "Coordinate-dependent 3 + 1 formulation of the General Relativity equations for a perfect fluid". General Relativity and Gravitation. 13 (6): 569–580. Bibcode:1981GReGr..13..569N. doi:10.1007/BF00757243. S2CID 122196359.
• Penrose, Roger (1965). "Gravitational Collapse and Space-Time Singularities". Physical Review Letters. 14 (3): 57–59. Bibcode:1965PhRvL..14...57P. doi:10.1103/PhysRevLett.14.57.
• Petrov, Alexey Z. (1969). Einstein Spaces. Oxford: Pergamon Press. ISBN 978-0-08-012315-8.
• Rugh, Svend E. (1994). "Chaos in the Einstein Equations -- characterization and importance?". Deterministic Chaos in General Relativity. Kananaskis, Alberta, Canada: Springer Science+Business Media New York. pp. 359–422. doi:10.1007/978-1-4757-9993-4. ISBN 978-1-4757-9995-8.
• Saotome, Ryo; Akhoury, Ratindranath; Garfinkle, David (2010). "Examining gravitational collapse with test scalar fields". Classical and Quantum Gravity. 27 (165019): 165019. arXiv:1004.3569. Bibcode:2010CQGra..27p5019S. doi:10.1088/0264-9381/27/16/165019. S2CID 55229333.
• Taub, A.H. (1951). "Empty space-times admitting a three parameter group of motions". Annals of Mathematics. Second Series. 53 (3): 472–490. Bibcode:1951AnMat..53..472T. doi:10.2307/1969567. ISSN 0003-486X. JSTOR 1969567. MR 0041565.
• Thorne, Kip (1994). Black Holes and Time Warps: Einstein's Outrageous Legacy. W W Norton. ISBN 978-0-393-31276-8.]; Kip Thorne (2015). Geometrodynamics: The Nonlinear Dynamics of Curved Spacetime (Video lecture). The Van Leer Jerusalem Institute.
• Uggla, Claes; van Elst, Henk; Wainwright, John; Ellis, George F.R. (2003). "Past attractor in inhomogeneous cosmology". Physical Review D. 68 (10): 103502. arXiv:gr-qc/0304002. Bibcode:2003PhRvD..68j3502U. doi:10.1103/PhysRevD.68.103502. S2CID 53635765.
• Weaver, Marsha; Isenberg, James; Berger, Beverly K. (1998). "Mixmaster behavior in inhomogeneous cosmological spacetimes". Physical Review Letters. 80 (14): 2984–2987. arXiv:gr-qc/9712055. Bibcode:1998PhRvL..80.2984W. doi:10.1103/PhysRevLett.80.2984. S2CID 119467400.
• Damour, Thibault (19 November 2015). The Structure of Cosmological Singularities (Video lecture). Institut Henri Poincaré.