
Según la leyenda, Pitágoras descubrió los fundamentos de la afinación musical al escuchar los sonidos de cuatro martillos de herrero , que producían consonancia y disonancia cuando se golpeaban simultáneamente. Según Nicómaco en su Enchiridion harmonices del siglo II d. C. , [1] Pitágoras se dio cuenta de que el martillo A producía consonancia con el martillo B cuando se golpeaban juntos, y el martillo C producía consonancia con el martillo A, pero los martillos B y C producían disonancia entre sí. El martillo D producía una consonancia tan perfecta con el martillo A que parecían estar "cantando" la misma nota. Pitágoras corrió a la herrería para descubrir por qué, y encontró que la explicación estaba en las proporciones de peso. Los martillos pesaban 12, 9, 8 y 6 libras respectivamente. Los martillos A y D estaban en una proporción de 2:1, que es la proporción de la octava . Los martillos B y C pesaban 8 y 9 libras. Sus proporciones con el martillo D eran (12:8 = 3:2 = quinta perfecta ) y (12:9 = 4:3 = cuarta perfecta ). El espacio entre B y C tiene una proporción de 9:8, que es igual a la nota musical entera, o intervalo de tono entero ( ).
La leyenda es, al menos con respecto a los martillos, demostrablemente falsa. Probablemente se trate de un cuento popular de Oriente Medio. [2] Estas proporciones son, de hecho, relevantes para la longitud de las cuerdas (por ejemplo, la de un monocordio ): utilizando estos intervalos fundadores, es posible construir la escala cromática y la escala diatónica básica de siete tonos utilizada en la música moderna, y Pitágoras bien podría haber influido en el descubrimiento de estas proporciones (de ahí que a veces se las denomine afinación pitagórica ), pero las proporciones no tienen la misma relación con el peso del martillo y los tonos producidos por ellos. [3] [4] Sin embargo, los cinceles accionados por martillo con la misma sección transversal muestran una proporción exacta entre la longitud o el peso y la frecuencia propia . [5]
Fuentes anteriores mencionan el interés de Pitágoras por la armonía y la proporción. Jenócrates (siglo IV a. C.), aunque no menciona la historia del herrero, hasta donde sabemos, describió el interés de Pitágoras en términos generales: "Pitágoras descubrió también que los intervalos en la música no surgen al margen del número, pues son una interrelación de cantidad con cantidad. Así que se propuso investigar bajo qué condiciones surgen los intervalos concordantes y los discordantes, y todo lo que está bien o mal afinado". [6] Cualesquiera que sean los detalles del descubrimiento de la relación entre la música y la proporción, se lo considera [7] como la primera descripción matemática empíricamente segura de un hecho físico. Como tal, es un símbolo de, y tal vez conduzca a, la concepción pitagórica de las matemáticas como el modus operandi de la naturaleza . [8] Como Aristóteles escribiría más tarde, "los pitagóricos construyen todo el universo a partir de números". [9] El Micrólogo de Guido de Arezzo repite la leyenda en el capítulo XX. [10]
Según la versión más antigua registrada [11] de la leyenda, Pitágoras, que vivió en el siglo VI a. C., buscaba una herramienta para medir las percepciones acústicas, de forma similar a cómo se miden las cantidades geométricas con un compás o las pesas con una balanza. Al pasar por una fragua donde cuatro (según una versión posterior, cinco) artesanos trabajaban con martillos, notó que cada golpe producía tonos de diferente tono , lo que daba lugar a armonías cuando se emparejaban. Pudo distinguir octava , quinta y cuarta . Solo un par, que formaba el intervalo entre cuarta y quinta (una segunda mayor ), lo percibió como disonante . Emocionado, corrió a la fragua para realizar experimentos. Allí, descubrió que la diferencia de tono no dependía de la forma del martillo, la posición del hierro golpeado o la fuerza del golpe. Más bien, podía asociar los tonos con los pesos de los martillos, que midió con precisión. Luego regresó a casa para continuar con los experimentos.
Colgó cuatro cuerdas de igual longitud, igual fuerza e igual torsión en sucesión en una clavija sujeta en diagonal a la esquina de las paredes, dándoles pesos diferentes mediante la fijación de pesos diferentes en la parte inferior. Luego golpeó las cuerdas en pares, y resonaron las mismas armonías que en la fragua. La cuerda con la carga más pesada de doce unidades, cuando se emparejó con la cuerda menos cargada que llevaba seis unidades, produjo una octava. Por lo tanto, era evidente que la octava se basaba en la relación 12:6, o 2:1. La cuerda más tensa produjo una quinta con la segunda cuerda más floja (ocho unidades), y una cuarta con la segunda cuerda más tensa (nueve unidades). De esto, se dedujo que la quinta se basaba en la relación 12:8, o 3:2, y la cuarta en la relación 12:9, o 4:3. Nuevamente, la relación de la segunda cuerda más tensa con respecto a la más floja, con 9:6, o 3:2, dio como resultado una quinta, y la relación de la segunda más floja con respecto a la más floja, con 8:6, o 4:3, dio como resultado una cuarta. Para el intervalo disonante entre la quinta y la cuarta, se reveló que se basaba en la relación 9:8, que coincidía con las mediciones de peso realizadas en la fragua. La octava resultó ser el producto de la quinta y la cuarta:
Pitágoras extendió luego el experimento a diversos instrumentos, experimentó con vasijas, flautas, triángulos , el monocordio , etc., encontrando siempre las mismas proporciones numéricas. Finalmente, introdujo la terminología comúnmente utilizada para el oído relativo.
Con la invención del monocordio para investigar y demostrar las armonías de pares de cuerdas con diferentes proporciones de longitudes enteras, se dice que Pitágoras introdujo un medio conveniente para ilustrar el fundamento matemático de la teoría musical que descubrió. El monocordio, llamado κανών (kanōn) en griego y regula en latín, es una caja resonante con una cuerda estirada sobre ella. Una escala de medición está unida a la caja. El dispositivo está equipado con un puente móvil, que permite dividir la longitud vibrante de la cuerda; la división se puede determinar con precisión utilizando la escala de medición. Esto permite la medición de intervalos. A pesar del nombre "monocordio", que significa "de una cuerda", también hubo monocordios de varias cuerdas que podían producir intervalos simultáneos. Sin embargo, no está claro cuándo se inventó el monocordio. Walter Burkert data este logro en una época posterior a la era de Aristóteles , quien aparentemente no conocía el dispositivo; por lo tanto, se introdujo mucho después de la muerte de Pitágoras. [12] Por otra parte, Leonid Zhmud sugiere que Pitágoras probablemente realizó su experimento, que condujo al descubrimiento de las proporciones numéricas, utilizando el monocordio. [13]
Hípaso de Metaponto , un pitagórico temprano (finales del siglo VI y principios del V a. C.), realizó investigaciones cuantitativas sobre los intervalos musicales. El experimento atribuido a Hípaso, que implicaba placas circulares de diferentes espesores que oscilaban libremente, es físicamente correcto, a diferencia de los supuestos experimentos de Pitágoras. No está claro si Arquitas de Tarento , un pitagórico importante de los siglos V/IV a. C., realizó experimentos relevantes. Probablemente era más un teórico que un practicante de la música, pero se refirió a las observaciones acústicas de sus predecesores. Los ejemplos musicales que cita en apoyo de su teoría acústica involucran instrumentos de viento; no menciona experimentos con instrumentos de cuerda o cuerdas individuales. Arquitas partió de la hipótesis errónea de que el tono depende de la velocidad de propagación del sonido y de la fuerza del impacto sobre el cuerpo que lo produce; en realidad, la velocidad del sonido es constante en un medio dado, y la fuerza solo afecta al volumen. [14]
Walter Burkert opina que, a pesar de su imposibilidad física, la leyenda no debe considerarse una invención arbitraria, sino que tiene un significado que se puede encontrar en la mitología griega . Los Dáctilos ideos , los inventores míticos de la herrería, fueron también, según el mito, los inventores de la música. Así pues, ya existía una tradición muy antigua que asociaba la herrería con la música, en la que los herreros míticos eran representados como poseedores del secreto de la música mágica. Burkert ve la leyenda de Pitágoras en los herreros como una transformación y racionalización tardía del antiguo mito de los Dáctilos: En la leyenda de Pitágoras, los herreros ya no aparecen como poseedores de un antiguo conocimiento mágico, sino que, sin pretenderlo, se convierten, aunque sin saberlo, en "maestros" de Pitágoras. [15]
En la Alta Edad Media , Isidoro de Sevilla se refirió al herrero bíblico Tubal como el inventor de la música; autores posteriores lo siguieron en esto. Esta tradición muestra una vez más la idea de una relación entre la herrería y la música, que también aparece en mitos y leyendas no europeos. [16] Tubal era el medio hermano de Jubal , quien era considerado el antepasado de todos los músicos. Ambos eran hijos de Lamec y, por lo tanto, nietos de Caín . En algunas tradiciones cristianas de la Edad Media, Jubal, que observaba a su hermano Tubal, era equiparado con Pitágoras. [17]
Otra explicación es la que propone Jørgen Raasted, siguiendo a Leonid Zhmud. La hipótesis de Raasted afirma que el punto de partida de la formación de la leyenda fue un informe sobre los experimentos de Hippasus. Hippasus utilizó vasos llamados "sphaírai". Esta palabra se confundió por error con "sphýrai" (martillos) debido a un error del escriba, y en lugar del nombre de Hippasus se utilizó el de Pitágoras como el creador de los experimentos. De ahí surgió la leyenda de la forja. [18]
Los números enteros 6, 8, 9 y 12, en relación al tono más bajo (número 12), corresponden a los intervalos puros de cuarta (número 9), quinta (número 8) y octava (número 6) en adelante:
El oído humano percibe estos intervalos puros como si no tuvieran pulsaciones , ya que el volumen de los tonos no varía. En las partituras musicales , estos cuatro tonos pitagóricos pueden expresarse, por ejemplo, con la secuencia melódica do' – fa' – sol' – do":

Si esta secuencia de tonos no se considera desde el tono más bajo, sino desde el más alto (número 6), también resultan los siguientes intervalos: una cuarta (número 8), una quinta (número 9) y una octava (número 12), en este caso, sin embargo, hacia abajo:
La quinta y la octava aparecen en relación con el tono fundamental en la serie armónica natural, pero no así la cuarta ni su equivalente en octava. Este intervalo de cuarta aparece en los instrumentos de viento metal sin válvula conocidos desde la antigüedad y en los sobretonos armónicos de los instrumentos de cuerda.
La investigación posterior de los intervalos formados por octavas, quintas y cuartas, y sus múltiplos, condujo finalmente de las escalas diatónicas con siete tonos diferentes ( escala heptatónica ) en la afinación pitagórica a una escala cromática con doce tonos. Los intervalos de Wolf en la afinación pitagórica planteaban un problema: en lugar de las quintas puras La♭-Mi♭ y Re♭-La♭, sonaban las quintas Sol♯-Mi♭ y Do♯-La♭, que estaban desafinadas por la coma pitagórica .
Con la llegada de la polifonía en la segunda mitad del siglo XV, además de la octava y la quinta, la tercera pura se volvió crucial para las tríadas mayores y menores. Aunque esta afinación no podía realizarse en un teclado de doce notas, podía lograrse bien en el temperamento de tono medio. Su desventaja era que no todas las tonalidades del círculo de quintas eran tocables. Para remediar esta deficiencia, se introdujeron las afinaciones temperadas, aunque con la desventaja de que la tercera pura sonaba más áspera en algunas tonalidades. Hoy en día, la mayoría de los instrumentos están afinados en temperamento igual con 12 teclas, de modo que las octavas son perfectamente puras, las quintas son casi puras y las terceras suenan ásperas.
En música, los cuatro tonos armónicos pitagóricos desempeñan un papel destacado en la escala pentatónica, en particular en los grados primero, cuarto, quinto y octavo de las escalas diatónicas (sobre todo en las mayores y menores) y en la composición de cadencias como tonos fundamentales de tónica, subdominante y dominante. Esta secuencia de tonos aparece a menudo en cadencias con los acordes correspondientes:

Los cuatro tonos pitagóricos aparecen en muchas composiciones. Los primeros tonos de las antífonas medievales "Ad te levavi" y "Factus est repentinamente" consisten esencialmente en los cuatro tonos pitagóricos, con la excepción de algunos adornos y notas altas. [19]
Otro ejemplo es el comienzo de la Passacaglia en do menor de Johann Sebastian Bach. El tema consta de quince tonos, de los cuales un total de diez tonos y, sobre todo, los cuatro últimos tonos se derivan de la secuencia.
Tono absoluto de los martillos
La frecuencia de resonancia de los martillos de acero que pueden ser movidos por manos humanas está generalmente en el rango ultrasónico y por lo tanto es inaudible. Pitágoras no podría haber percibido estos tonos, especialmente cuando los martillos tenían una diferencia de tono de una octava.
Frecuencia de vibración en función del peso del martillo
La frecuencia de vibración de un cuerpo sólido que oscila libremente, como por ejemplo una onda longitudinal , no suele ser proporcional a su peso o volumen, sino que es proporcional a su longitud, que varía con una geometría similar solo con la raíz cúbica del volumen.
Para los martillos pitagóricos, se aplican los siguientes números de relación para una geometría similar (valores en unidades arbitrarias):
El tono en relación con la tensión de la cuerda
La suposición de que la frecuencia de vibración de una cuerda es proporcional a la tensión no es correcta. Más bien, la frecuencia de vibración es proporcional a la raíz cuadrada de la tensión. Para duplicar la frecuencia de vibración, se debe aplicar cuatro veces la tensión y, por lo tanto, se debe colgar un peso cuatro veces más pesado en una cuerda.
El hecho de que un tono con la frecuencia fundamental esté en consonancia con un segundo tono con un múltiplo entero (con y ) de esta frecuencia fundamental es inmediatamente evidente por el hecho de que los máximos y mínimos de las vibraciones del tono son sincrónicos en el tiempo, pero también se puede explicar de la siguiente manera:
La frecuencia de pulsación de los dos tonos que suenan simultáneamente se calcula matemáticamente a partir de la diferencia entre las frecuencias de estos dos tonos y se puede escuchar como un tono combinado:
(ver Descripción matemática del ritmo ).
Esta diferencia es en sí misma una relación entera con la frecuencia fundamental :
Para todos los múltiplos enteros de la frecuencia fundamental del segundo tono, existen también múltiplos enteros de la frecuencia de pulsación (véase la tabla de la derecha), de modo que todos los tonos suenan consonantes.
Incluso para dos tonos cuyas frecuencias están en una razón racional de a , existe una consonancia. La frecuencia del segundo tono viene dada por:
En consecuencia, la frecuencia de batido de los dos tonos que suenan simultáneamente viene dada por:
En estas condiciones, la frecuencia fundamental es siempre un múltiplo entero de la frecuencia de batido (véase la tabla de la derecha), por lo que no se produce disonancia .
Para estimar un bloque de metal, consideremos un prisma rectangular homogéneo con una longitud máxima y hecho de un material con una velocidad del sonido . Para el modo de vibración a lo largo de su lado más largo ( oscilación longitudinal ), tiene la frecuencia natural más baja con antinodos en ambos extremos y un nodo en el medio. [20]
.
Por lo tanto, el tono es independiente de la masa y del área de la sección transversal del prisma, y el área de la sección transversal puede incluso variar. Además, la fuerza y la velocidad al golpear el cuerpo tampoco influyen. Al menos este hecho corresponde a la observación atribuida a Pitágoras de que el tono percibido no dependía de las manos (y, por lo tanto, de las fuerzas) de los artesanos.
Los cuerpos con una geometría más compleja , como campanas , tazas o cuencos , que incluso pueden estar llenos de líquidos, tienen frecuencias naturales que requieren descripciones físicas considerablemente más elaboradas, ya que no solo se debe considerar la forma sino también el espesor de la pared o incluso el lugar de impacto. En estos casos, también pueden excitarse y ser audibles oscilaciones transversales .

Un mazo de gran tamaño (la velocidad del sonido en el acero es de aproximadamente 5000 metros por segundo) con una longitud de cabeza de 0,2 metros tiene una frecuencia natural de 12,5 kilohercios. Con una sección transversal cuadrada de 0,1 metros cuadrados (0,1 metros por 0,1 metros), tendría una masa inusualmente grande de casi 16 kilogramos con una densidad de 7,86 gramos por centímetro cúbico. Las frecuencias superiores a aproximadamente 15 kilohercios ya no son percibidas por muchas personas (véase el umbral auditivo ); por lo tanto, la frecuencia natural de un martillo tan grande es apenas audible. Los martillos con cabezas más cortas tienen frecuencias naturales aún más altas que, por lo tanto, son inaudibles.
Un gran yunque de acero con una longitud de 0,5 metros tiene una frecuencia natural de sólo 5 kilohercios y, por lo tanto, es fácilmente audible.
Existen diversas composiciones en las que el compositor especifica el uso de yunques como instrumentos musicales. Especialmente conocidas son las dos óperas del drama musical El anillo del nibelungo de Richard Wagner :
Los materiales con una velocidad de sonido menor que el acero, como el granito o el latón , producen frecuencias aún más bajas con una geometría congruente. En cualquier caso, los yunques no se mencionan en los primeros relatos y los sonidos audibles de los yunques se atribuyen a los martillos en las versiones posteriores de la leyenda.


Es posible comparar varillas de metal, como los cinceles que utilizan los albañiles o las cuñas para romper piedras, para llegar a una observación similar a la atribuida a Pitágoras, a saber, que la frecuencia de vibración de las herramientas es proporcional a su peso . Si las varillas de metal, despreciando los bordes cortantes cónicos, tienen todas la misma área de sección transversal uniforme A pero diferentes longitudes l , entonces su peso es proporcional a la longitud y, por lo tanto, también a la frecuencia de vibración, siempre que las varillas de metal se exciten a vibraciones longitudinales mediante golpes a lo largo del eje longitudinal (se pueden encontrar buenos ejemplos en el recuadro de la derecha). [21]
Para los osciladores de flexión, como los diapasones o las placas de los metalófonos , se aplican condiciones y leyes diferentes; por lo tanto, estas consideraciones no se aplican a ellos.

Las cuerdas pueden fijarse en dos extremos, cada uno sobre un puente . A diferencia de un sólido con vibraciones longitudinales, los dos puentes establecen las condiciones de contorno para dos puntos nodales de vibración; por lo tanto, el nodo vibracional se ubica en el medio.
La frecuencia natural y, por lo tanto, el tono de las cuerdas con longitud no son proporcionales a la tensión , sino a la raíz cuadrada de la tensión. Además, la frecuencia aumenta con un mayor peso de tracción y, por lo tanto, una mayor tensión, en lugar de disminuir: [22]
Sin embargo, la frecuencia de vibración es inversamente proporcional a la longitud de la cuerda a tensión constante, lo que puede demostrarse directamente con el monocordio , supuestamente inventado por Pitágoras.

La primera mención del descubrimiento de Pitágoras de la base matemática de los intervalos musicales se encuentra en el platónico Jenócrates (siglo IV a. C.); como solo se trata de una cita de una obra perdida de este pensador, no está claro si conocía la leyenda de la forja. [23] En el siglo IV a. C. ya se expresaban críticas a la teoría pitagórica de los intervalos, aunque sin referencia a la leyenda de Pitágoras; el filósofo y teórico musical Aristóxeno la consideraba falsa.

La versión más antigua registrada de la leyenda fue presentada siglos después de la época de Pitágoras por el neopitagórico Nicómaco de Gerasa , quien en el siglo I o II d. C. documentó la historia en su Harmonikḗ Encheirídion ("Manual de armonía"). Se basó en el filósofo Filolao , un pitagórico del siglo V a. C., para su representación de las proporciones numéricas en la teoría musical. [24]
El famoso matemático y teórico musical Ptolomeo (siglo II d. C.) conocía el método de pesaje transmitido por la leyenda, pero lo rechazó. Sin embargo, no reconoció la falsedad de los experimentos de pesaje; solo criticó sus inexactitudes en comparación con las mediciones precisas en el monocordio. [25] Es probable que no obtuviera su conocimiento de la tradición legendaria de Nicómaco, sino de una fuente más antigua, hoy perdida. [26]
El teórico musical de la época imperial, Gaudencio , describió la leyenda en su Harmonikḗ Eisagōgḗ ("Introducción a la armonía"), en una versión ligeramente más corta que la de Nicómaco. El filósofo neoplatónico Jámblico de Calcis , que trabajó como profesor de filosofía a finales del siglo III y principios del IV, escribió una biografía de Pitágoras titulada Sobre la vida pitagórica , en la que reprodujo la leyenda del herrero en la versión de Nicómaco.
En la primera mitad del siglo V, el escritor Macrobio discutió extensamente la leyenda del herrero en su comentario al Somnium Scipionis de Cicerón , que describió de manera similar a Nikomachos. [27]

El libro de texto De institutione musica ("Introducción a la música"), escrito a principios del siglo VI, que tuvo la mayor repercusión entre los teóricos de la música antigua que retomaron esta narración, fue el de Boecio , en el que describe inicialmente los esfuerzos de Pitágoras por comprender en la fragua y luego en casa. [28] No está claro si se basó en el relato de Nikómaco o en otra fuente. En contraste con toda la tradición anterior, habla de cinco martillos en lugar de los cuatro que suponían los autores anteriores. Afirma que Pitágoras rechazó el quinto martillo porque resultaba en disonancia con todos los demás martillos. Según el relato de Boecio (al igual que con Macrobio), Pitágoras puso a prueba su suposición inicial de que la diferencia en el sonido se debía a la diferente fuerza en los brazos de los hombres haciendo que los herreros intercambiaran los martillos, lo que llevó a su refutación. En cuanto a los experimentos en casa de Pitágoras, Boecio escribe que el filósofo primero colgó cuerdas con pesos iguales a los de los martillos en la fragua y luego experimentó con tubos y copas, y todos los experimentos arrojaron los mismos resultados que los iniciales con los martillos. Utilizando la leyenda como base, Boecio aborda la cuestión de la fiabilidad de las percepciones sensoriales en términos de ciencia y epistemología. El punto crucial es que Pitágoras fue impulsado inicialmente por la percepción sensorial para formular su pregunta e hipótesis, y a través de la prueba empírica de hipótesis, llegó a una certeza irrefutable. El camino hacia el conocimiento iba desde la percepción sensorial a la hipótesis inicial, que resultó ser errónea, luego a la formación de una opinión correcta y finalmente a su verificación. Boecio reconoce la necesidad y el valor de la percepción sensorial y la formación de una opinión en el camino hacia la comprensión, aunque como platónico , es inherentemente escéptico de la percepción sensorial debido a su propensión al error. Para él, el conocimiento genuino surge sólo cuando se capta la regularidad, lo que permite al investigador emanciparse de su dependencia inicial de la percepción sensorial poco fiable. El juicio del investigador no debe basarse únicamente en el juicio sensorial derivado de la experiencia empírica, sino que sólo debe emitirse una vez que haya encontrado una regla mediante la deliberación que le permita situarse más allá del ámbito del posible engaño sensorial. [29]
En el siglo VI, el erudito Casiodoro escribió en sus Institutiones que Gaudencio atribuyó los inicios «de la música» a Pitágoras en su relato de la leyenda del herrero. Se refería a la teoría musical, como también lo había hecho Jámblico, quien, con referencia al relato del herrero y a los experimentos allí descritos, se había referido a Pitágoras como el inventor «de la música». [30]
En la Alta Edad Media , Isidoro de Sevilla mencionó la leyenda del herrero en sus Etimologías , que se convirtieron en una obra de referencia fundamental para los cultos de la Edad Media. Mencionó brevemente la leyenda, adoptando la redacción de Casiodoro y también designando a Pitágoras como el inventor de la música. [31] Como Casiodoro e Isidoro eran autoridades de primer orden en la Edad Media, se extendió la idea de que Pitágoras había descubierto la ley fundamental de la música y, por lo tanto, había sido su fundador. A pesar de estas afirmaciones tan generales, los teóricos de la música medieval asumieron que la música había existido antes de Pitágoras y que la "invención de la música" se refería al descubrimiento de sus principios. [32]
En el siglo IX, el musicólogo Aureliano de Réomé contó la leyenda en su Musica disciplina ("Teoría de la música"). El relato de Aureliano fue seguido en el siglo X por Regino de Prüm en su obra De harmonica institutione ("Introducción a la teoría armónica"). Ambos enfatizaron que Pitágoras había tenido la oportunidad de hacer su descubrimiento en la fragua del herrero por una providencia divina. [33] En la antigüedad, Nicómaco y Jámblico ya habían hablado de una providencia demoníaca , y Boecio la había transformado en un decreto divino.
En el siglo XI el material legendario fue procesado en la Carmina Cantabrigiensia . [34]

En la primera mitad del siglo XI, Guido de Arezzo , el teórico musical más famoso de la Edad Media, contó la leyenda del herrero en el capítulo final de su Micrologus , basándose en la versión de Boecio, a quien nombró específicamente. Guido comentó al principio: Tampoco nadie habría descubierto nada cierto sobre este arte (la música) si, al final, la bondad divina no hubiera provocado el siguiente evento a instancias suyas. Atribuyó el hecho de que los martillos pesaran 12, 9, 8 y 6 unidades y, por lo tanto, produjeran un sonido armonioso a la providencia de Dios. [35] También mencionó que Pitágoras, a partir de su descubrimiento, había inventado el monocordio, pero no entró en detalles sobre sus propiedades.
La obra De musica de Johannes Cotto (también conocido como John Cotton o Johannes Afflighemensis) fue ilustrada con la escena del herrero alrededor de 1250 por un iluminador de libros anónimo en la abadía cisterciense de Aldersbach . [36]
Entre los teóricos musicales medievales que contaron la leyenda de la forja según la versión de Boecio se encontraban también Juan Gil de Zámora (Johannes Aegidius von Zamora), activo a finales del siglo XIII y principios del XIV, Johannes de Muris y Simon Tunstede en el siglo XIV, y Adam von Fulda en el umbral del periodo moderno temprano en el siglo XV.
Como oponente de la concepción pitagórica, que sostenía que las consonancias se basaban en ciertas proporciones numéricas, Johannes de Grocheio surgió en el siglo XIII, partiendo de una perspectiva aristotélica. Aunque afirmó explícitamente que Pitágoras había descubierto los principios de la música, y contó la leyenda de la fragua citando a Boecio, a quien consideraba digno de confianza, rechazó la teoría pitagórica de la consonancia, que quería reducir a una expresión meramente metafórica. [37]


Franchino Gaffurio publicó en Nápoles en 1480 su obra Theoricum opus musice discipline (Teoría teórica de la música), que fue revisada y republicada en 1492 con el título Theorica musice (Teoría de la música). En ella presentó una versión de la leyenda de la fragua que superaba en detalle a todas las anteriores. Basó su versión en la de Boecio y añadió un sexto martillo para incluir en la narración el mayor número posible de tonos de la octava. En cuatro representaciones pictóricas presentó instrumentos musicales o generadores de sonido, cada uno con seis tonos armónicos, e indicó en las etiquetas los números 4, 6, 8, 9, 12 y 16 asociados a los tonos. Además de las cuatro proporciones tradicionales de la leyenda (6, 8, 9 y 12), añadió 4 y 16, que representan un tono una quinta más bajo y otro tono una cuarta más alto. La secuencia completa de tonos se extiende ahora no sólo sobre una, sino sobre dos octavas. Estos números corresponden, por ejemplo, a los tonos fa – do' – fa' – sol' – do" – fa:
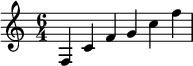
El pintor Erhard Sanßdorffer recibió en 1546 el encargo de crear un fresco en el castillo de Büdingen, en Hesse, que se encuentra bien conservado y que, como un compendio, representa la historia de la música a partir de la forja de Pitágoras. [38]
Gioseffo Zarlino también contó la leyenda en su obra Le istitutioni harmoniche ("Los fundamentos de la armonía"), que publicó en 1558; al igual que Gaffurio, basó su relato en la versión de Boecio. [39]
El teórico musical Vincenzo Galilei, padre de Galileo Galilei, publicó en 1589 su tratado Discorso intorno all'opere di messer Gioseffo Zarlino ("Discurso sobre las obras del señor Gioseffo Zarlino"), que iba dirigido contra las opiniones de su maestro Zarlino. En él, señalaba que la información de la leyenda sobre la carga de las cuerdas con pesos no es exacta.[1]

En 1626, el Thesaurus philopoliticus de Daniel Meisner presentó un grabado en cobre titulado "Duynkirchen" de Eberhard Kieser, que representa únicamente a tres herreros en un yunque. El epígrafe en latín y alemán dice:[2]
Unos años más tarde, el asunto se aclaró definitivamente cuando Galileo Galilei y Marin Mersenne descubrieron las leyes de las vibraciones de las cuerdas. En 1636, Mersenne publicó su Harmonie universelle, en la que explicaba el error físico de la leyenda: la frecuencia de vibración no es proporcional a la tensión, sino a su raíz cuadrada.[3]
Varios compositores incorporaron esta temática en sus obras, entre ellos Georg Muffat a finales del siglo XVII. [40] y Rupert Ignaz Mayr . [41]
Incluso en el siglo XIX, Hegel asumió la exactitud física de las supuestas medidas mencionadas en la leyenda de Pitágoras en sus conferencias sobre la historia de la filosofía. [42]
Werner Heisenberg destacó en un ensayo publicado por primera vez en 1937 que el "descubrimiento de la determinación matemática de la armonía" pitagórico se basa en "la idea del poder significativo de las estructuras matemáticas", una "idea fundamental que la ciencia exacta moderna ha heredado de la antigüedad"; el descubrimiento atribuido a Pitágoras pertenece "a los impulsos más fuertes de la ciencia humana en general". [43]
Más recientemente, se han publicado relatos en los que se reproduce la leyenda acríticamente sin hacer referencia a su falsedad física e histórica. [44] Por ejemplo, en el libro de no ficción El quinto martillo: Pitágoras y la disarmonía del mundo de Daniel Heller-Roazen . [45]
los pitagóricos construyen todo el universo a partir de números.
Erant antiquitus instrumenta incerta. et canentium multitudo sed ceca. Nullus enim hominum uocum diferenciadas. et simphoniae descripciónem poterat aliqua argumentatione colligere. neque posset unquam certum aliquid de hac arte cognoscere. nisi diuina pietas tandem quod sequitur suo nutu disponeret. Cum Phitagoras quidam magnus philosophus forte iter ageret. uentum est ad fabricam. in qua super unam incudem quinque mallei feriebant. Quorum suauem miratus concordiam philosophus accessit. primumque in manuum uarietate sperans [f.20r] uim soni ac modulationis existere. mutauit malleos. Quo facto. sua uis quemque secuta est. Subtracto itaque uno qui dissonus erat a ceteris. alios ponderauit. Mirumque in modum diuino nutu primus .XII. segundo .VIII. tercio .VIII. cuarto .VI. nescio quibus ponderibus appendebant. Cognouit itaque in numerorum proporcionale et collatione musicae uersari scientiam. Erat enim ea constitutio in quattuor malleis. quae modo est in quattuor litteris .ADEa Denique si A habeat .XII. y D VIIII. sintque quaternarii in pro passu. habebit .A. en .XII. ternarios .IIII. et D. en .VIII. ternarios .III. Ecce diatessaron. Rursus cum habeat A .XII. si tenea E. VIII. cuaternarios passus tres habebit .A. duos uero E. et diapente patet. Sint iterum .XII en A. et .VI. in alteram a. Senarius medietas est duodenarii. sicut et a acuta alterius A medietate colligitur. Adest ergo diapasón. Cum igitur ipsa .a. ad D. diatessaron ad e diapente. alteri uero a diapasón reddit. D quoque ad e tonum. ad utrumque A a diatessaron. et diapente sonat. Et E etiam ad D. tonum utrique Aa diapente et diatessaron mandat. a uero acuta cum A diapasón. cum D diapente. cum E diatessaron sonat. quae in supra dictis numeris curiosus perscrutator inuenit. Hinc enim incipiens Boetius panditor huius artis. multam miramque et difficillimam huius artis cum numerorum proporcionale concordiam demonstrauit. [f.20v] ¿Quid plura? Per supra dictas species uces ordinans. monocordum primus ille Phitagoras quattuor neruorum composuit. in quo quia non est lasciuia. sed diligenter aperta artis notitia. sapientibus en la comuna placuit. atque usque in hunc diem ars paulatim crescendo conualuit. ipso doctore sempre humanas tenebras illustrante. cuius summa sapientia per cuncta uiget secula.