Onda estacionaria

Onda que permanece en una posición constante

Animación de una onda estacionaria ( roja ) creada por la superposición de una onda que se desplaza hacia la izquierda ( azul ) y otra que se desplaza hacia la derecha ( verde )

En física , una onda estacionaria , también conocida como onda estacionaria , es una onda que oscila en el tiempo pero cuyo perfil de amplitud pico no se mueve en el espacio. La amplitud pico de las oscilaciones de la onda en cualquier punto del espacio es constante con respecto al tiempo, y las oscilaciones en diferentes puntos a lo largo de la onda están en fase . Las ubicaciones en las que el valor absoluto de la amplitud es mínimo se denominan nodos , y las ubicaciones en las que el valor absoluto de la amplitud es máximo se denominan antinodos.

Las ondas estacionarias fueron descritas científicamente por primera vez por Michael Faraday en 1831. Faraday observó ondas estacionarias en la superficie de un líquido en un recipiente vibrante . ^{[1] [2]} Franz Melde acuñó el término "onda estacionaria" (en alemán: stehende Welle o Stehwelle ) alrededor de 1860 y demostró el fenómeno en su experimento clásico con cuerdas vibrantes. ^{[3] [4] [5] [6]}

Este fenómeno puede ocurrir porque el medio se mueve en dirección opuesta al movimiento de la onda, o puede surgir en un medio estacionario como resultado de la interferencia entre dos ondas que viajan en direcciones opuestas. La causa más común de las ondas estacionarias es el fenómeno de resonancia , en el que las ondas estacionarias se producen dentro de un resonador debido a la interferencia entre ondas reflejadas de ida y vuelta a la frecuencia de resonancia del resonador .

Para ondas de igual amplitud que viajan en direcciones opuestas, en promedio no hay propagación neta de energía .

Medio en movimiento

• Kayakistas surfeando en una ola estacionaria en Great Falls Park
• Desembocadura del río Carmelo : Se forman ondas estacionarias donde el río Carmelo se encuentra con el Océano Pacífico.

Como ejemplo del primer tipo, en determinadas condiciones meteorológicas se forman ondas estacionarias en la atmósfera al abrigo de las cadenas montañosas, ondas que suelen ser aprovechadas por los pilotos de planeadores .

Las ondas estacionarias y los saltos hidráulicos también se forman en rápidos de ríos de corriente rápida y corrientes de marea como el maelstrom de Saltstraumen . Un requisito para esto en las corrientes de ríos es un agua que fluye con poca profundidad en la que la inercia del agua vence a su gravedad debido a la velocidad de flujo supercrítico ( número de Froude : 1,7 – 4,5, superando 4,5 resulta en una onda estacionaria directa ^[7] ) y, por lo tanto, no es frenada significativamente por el obstáculo ni empujada hacia un lado. Muchas olas estacionarias de ríos son populares para surfear en ríos .

Ondas opuestas

Como ejemplo del segundo tipo, una onda estacionaria en una línea de transmisión es una onda en la que la distribución de corriente , voltaje o intensidad de campo se forma por la superposición de dos ondas de la misma frecuencia que se propagan en direcciones opuestas. El efecto es una serie de nodos ( desplazamiento cero ) y antinodos ( desplazamiento máximo ) en puntos fijos a lo largo de la línea de transmisión. Una onda estacionaria de este tipo puede formarse cuando una onda se transmite a un extremo de una línea de transmisión y se refleja desde el otro extremo por un desajuste de impedancia , es decir , una discontinuidad, como un circuito abierto o un cortocircuito . ^[8] El fallo de la línea para transferir energía a la frecuencia de onda estacionaria normalmente dará como resultado una distorsión de atenuación .

En la práctica, las pérdidas en la línea de transmisión y otros componentes hacen que nunca se consiga una reflexión perfecta ni una onda estacionaria pura. El resultado es una onda estacionaria parcial , que es una superposición de una onda estacionaria y una onda viajera. El grado en que la onda se asemeja a una onda estacionaria pura o a una onda viajera pura se mide mediante la relación de ondas estacionarias (SWR). ^[9]

Otro ejemplo son las ondas estacionarias en mar abierto , formadas por olas con el mismo período que se mueven en direcciones opuestas. Estas pueden formarse cerca de centros de tormentas o por la reflexión de un oleaje en la costa, y son la fuente de microbaromos y microsismos .

Descripción matemática

En esta sección se consideran casos representativos unidimensionales y bidimensionales de ondas estacionarias. En primer lugar, un ejemplo de una cuerda de longitud infinita muestra cómo ondas idénticas que viajan en direcciones opuestas interfieren para producir ondas estacionarias. A continuación, dos ejemplos de cuerdas de longitud finita con diferentes condiciones de contorno demuestran cómo las condiciones de contorno restringen las frecuencias que pueden formar ondas estacionarias. A continuación, el ejemplo de las ondas sonoras en una tubería demuestra cómo se pueden aplicar los mismos principios a las ondas longitudinales con condiciones de contorno análogas.

Las ondas estacionarias también pueden ocurrir en resonadores bidimensionales o tridimensionales . Con ondas estacionarias en membranas bidimensionales como parches de tambor , ilustradas en las animaciones anteriores, los nodos se convierten en líneas nodales, líneas en la superficie en la que no hay movimiento, que separan regiones que vibran con fase opuesta. Estos patrones de líneas nodales se denominan figuras de Chladni . En resonadores tridimensionales, como cajas de sonido de instrumentos musicales y resonadores de cavidad de microondas , hay superficies nodales. Esta sección incluye un ejemplo de onda estacionaria bidimensional con un límite rectangular para ilustrar cómo extender el concepto a dimensiones superiores.

Onda estacionaria en una cuerda de longitud infinita

Para comenzar, considere una cuerda de longitud infinita a lo largo del eje x que puede estirarse transversalmente en la dirección y .

Para una onda armónica que viaja hacia la derecha a lo largo de la cuerda, el desplazamiento de la cuerda en la dirección y en función de la posición x y el tiempo t es ^[10]

${\displaystyle y_{\text{R}}(x,t)=y_{\text{max}}\sin \left({2\pi x \over \lambda }-\omega t\right).}$

El desplazamiento en la dirección y para una onda armónica idéntica que viaja hacia la izquierda es

${\displaystyle y_{\text{L}}(x,t)=y_{\text{max}}\sin \left({2\pi x \over \lambda }+\omega t\right),}$

dónde

• y _max es la amplitud del desplazamiento de la cuerda para cada onda,
• ω es la frecuencia angular o equivalentemente 2π veces la frecuencia f ,
• λ es la longitud de onda de la onda.

Para ondas idénticas que viajan hacia la derecha y hacia la izquierda en la misma cuerda, el desplazamiento total de la cuerda es la suma de y _R e y _L ,

${\displaystyle y(x,t)=y_{\text{R}}+y_{\text{L}}=y_{\text{max}}\sin \left({2\pi x \over \lambda }-\omega t\right)+y_{\text{max}}\sin \left({2\pi x \over \lambda }+\omega t\right).}$

Utilizando la identidad trigonométrica de suma y producto , ${\displaystyle \sin a+\sin b=2\sin \left({a+b \over 2}\right)\cos \left({a-b \over 2}\right)}$

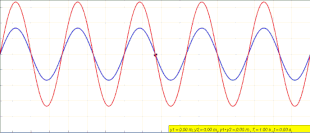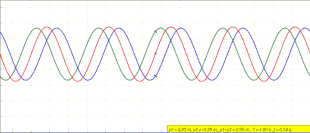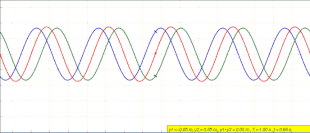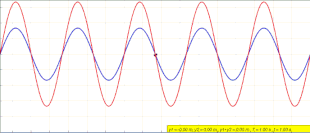
La ecuación ( 1 ) no describe una onda viajera. En cualquier posición x , y ( x , t ) simplemente oscila en el tiempo con una amplitud que varía en la dirección x como . ^[10] La animación al comienzo de este artículo representa lo que está sucediendo. A medida que la onda azul que viaja hacia la izquierda y la onda verde que viaja hacia la derecha interfieren, forman la onda roja estacionaria que no viaja y, en cambio, oscila en el mismo lugar. ${\displaystyle 2y_{\text{max}}\sin \left({2\pi x \over \lambda }\right)}$

Como la cuerda tiene una longitud infinita, no tiene ninguna condición límite para su desplazamiento en cualquier punto a lo largo del eje x . Como resultado, se puede formar una onda estacionaria a cualquier frecuencia.

En posiciones en el eje x que son múltiplos pares de un cuarto de longitud de onda,

${\displaystyle x=\ldots ,-{3\lambda \over 2},\;-\lambda ,\;-{\lambda \over 2},\;0,\;{\lambda \over 2},\;\lambda ,\;{3\lambda \over 2},\ldots }$

La amplitud es siempre cero. Estas posiciones se denominan nodos . En las posiciones del eje x que son múltiplos impares de un cuarto de longitud de onda

${\displaystyle x=\ldots ,-{5\lambda \over 4},\;-{3\lambda \over 4},\;-{\lambda \over 4},\;{\lambda \over 4},\;{3\lambda \over 4},\;{5\lambda \over 4},\ldots }$

La amplitud es máxima, con un valor de dos veces la amplitud de las ondas que viajan hacia la derecha y hacia la izquierda que interfieren para producir este patrón de onda estacionaria. Estas ubicaciones se denominan antinodos . La distancia entre dos nodos o antinodos consecutivos es la mitad de la longitud de onda, λ /2.

Onda estacionaria en una cuerda con dos extremos fijos

A continuación, considere una cuerda con extremos fijos en x = 0 y x = L . La cuerda tendrá algo de amortiguamiento a medida que se estira por ondas viajeras, pero suponga que el amortiguamiento es muy pequeño. Suponga que en el extremo fijo x = 0 se aplica una fuerza sinusoidal que impulsa la cuerda hacia arriba y hacia abajo en la dirección y con una pequeña amplitud a una frecuencia f . En esta situación, la fuerza impulsora produce una onda que viaja hacia la derecha. Esa onda se refleja en el extremo fijo derecho y viaja de regreso a la izquierda, se refleja nuevamente en el extremo fijo izquierdo y viaja de regreso a la derecha, y así sucesivamente. Finalmente, se alcanza un estado estable donde la cuerda tiene ondas que viajan hacia la derecha y hacia la izquierda idénticas como en el caso de longitud infinita y la potencia disipada por amortiguamiento en la cuerda es igual a la potencia suministrada por la fuerza impulsora, por lo que las ondas tienen una amplitud constante.

La ecuación ( 1 ) todavía describe el patrón de onda estacionaria que se puede formar en esta cuerda, pero ahora la ecuación ( 1 ) está sujeta a condiciones de contorno donde y = 0 en x = 0 y x = L porque la cuerda está fija en x = L y porque asumimos que la fuerza impulsora en el extremo fijo x = 0 tiene una amplitud pequeña. Comprobando los valores de y en los dos extremos,

${\displaystyle y(0,t)=0,}$

${\displaystyle y(L,t)=2y_{\text{max}}\sin \left({2\pi L \over \lambda }\right)\cos(\omega t)=0.}$

Ondas estacionarias en una cuerda: el modo fundamental y los primeros 5 armónicos .

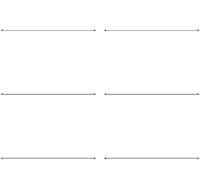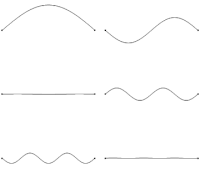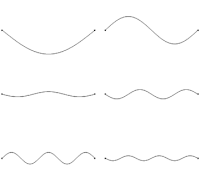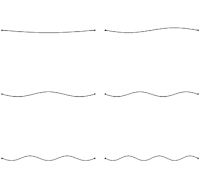
Esta condición de contorno tiene la forma de la formulación de Sturm-Liouville . La última condición de contorno se satisface cuando se da L , por lo que la condición de contorno restringe la longitud de onda de las ondas estacionarias a ^[11] ${\displaystyle \sin \left({2\pi L \over \lambda }\right)=0}$

${\displaystyle n=1,2,3,\ldots }$

Las ondas solo pueden formar ondas estacionarias en esta cuerda si tienen una longitud de onda que satisface esta relación con L . Si las ondas viajan con velocidad v a lo largo de la cuerda, entonces, equivalentemente, la frecuencia de las ondas estacionarias está restringida a ^{[11] [12]}

${\displaystyle f={\frac {v}{\lambda }}={\frac {nv}{2L}}.}$

La onda estacionaria con n = 1 oscila a la frecuencia fundamental y tiene una longitud de onda que es el doble de la longitud de la cuerda. Los valores enteros más altos de n corresponden a modos de oscilación llamados armónicos o sobretonos . Cualquier onda estacionaria en la cuerda tendrá n + 1 nodos, incluidos los extremos fijos, y n antinodos.

Para comparar los nodos de este ejemplo con la descripción de los nodos para ondas estacionarias en la cuerda de longitud infinita, la ecuación ( 2 ) se puede reescribir como

${\displaystyle \lambda ={\frac {4L}{n}},}$

${\displaystyle n=2,4,6,\ldots }$

En esta variación de la expresión para la longitud de onda, n debe ser par. Al multiplicar en cruz, vemos que, como L es un nodo, es un múltiplo par de un cuarto de longitud de onda.

${\displaystyle L={\frac {n\lambda }{4}},}$

${\displaystyle n=2,4,6,\ldots }$

Este ejemplo demuestra un tipo de resonancia y las frecuencias que producen ondas estacionarias pueden denominarse frecuencias resonantes . ^{[11] [13] [14]}

Onda estacionaria en una cuerda con un extremo fijo

Análisis transitorio de una onda viajera amortiguada que se refleja en un límite

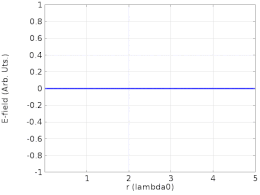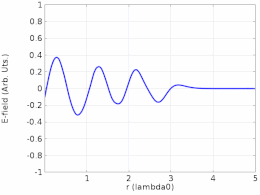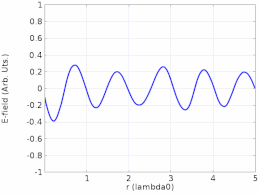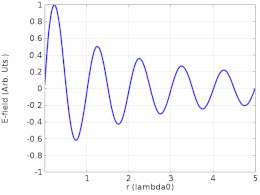
A continuación, considere la misma cuerda de longitud L , pero esta vez solo está fija en x = 0 . En x = L , la cuerda es libre de moverse en la dirección y . Por ejemplo, la cuerda podría estar atada en x = L a un anillo que puede deslizarse libremente hacia arriba y hacia abajo por un poste. La cuerda nuevamente tiene una pequeña amortiguación y es impulsada por una pequeña fuerza impulsora en x = 0 .

En este caso, la ecuación ( 1 ) todavía describe el patrón de onda estacionaria que se puede formar en la cuerda, y la cuerda tiene la misma condición de contorno de y = 0 en x = 0. Sin embargo, en x = L donde la cuerda puede moverse libremente debería haber un antinodo con amplitud máxima de y . De manera equivalente, esta condición de contorno del "extremo libre" se puede expresar como ∂y/∂x = 0 en x = L , que tiene la forma de la formulación de Sturm–Liouville . La intuición para esta condición de contorno ∂y/∂x = 0 en x = L es que el movimiento del "extremo libre" seguirá al del punto a su izquierda.

Revisando la ecuación ( 1 ), para x = L la mayor amplitud de y ocurre cuando ∂y/∂x = 0 , o

${\displaystyle \cos \left({2\pi L \over \lambda }\right)=0.}$

Esto da como resultado un conjunto de longitudes de onda diferente al del ejemplo de los dos extremos fijos. Aquí, la longitud de onda de las ondas estacionarias está restringida a

${\displaystyle \lambda ={\frac {4L}{n}},}$

${\displaystyle n=1,3,5,\ldots }$

De manera equivalente, la frecuencia está restringida a

${\displaystyle f={\frac {nv}{4L}}.}$

En este ejemplo, n solo toma valores impares. Como L es un antinodo, es un múltiplo impar de un cuarto de longitud de onda. Por lo tanto, el modo fundamental en este ejemplo solo tiene un cuarto de un ciclo sinusoidal completo: cero en x = 0 y el primer pico en x = L ; el primer armónico tiene tres cuartos de un ciclo sinusoidal completo, y así sucesivamente.

Este ejemplo también demuestra un tipo de resonancia y las frecuencias que producen ondas estacionarias se denominan frecuencias resonantes .

Onda estacionaria en una tubería

Considere una onda estacionaria en una tubería de longitud L. El aire dentro de la tubería sirve como medio para las ondas sonoras longitudinales que viajan hacia la derecha o hacia la izquierda a través de la tubería. Mientras que las ondas transversales en la cuerda de los ejemplos anteriores varían en su desplazamiento perpendicular a la dirección del movimiento de la onda, las ondas que viajan a través del aire en la tubería varían en términos de su presión y desplazamiento longitudinal a lo largo de la dirección del movimiento de la onda. La onda se propaga comprimiendo y expandiendo alternativamente el aire en segmentos de la tubería, lo que desplaza el aire ligeramente de su posición de reposo y transfiere energía a los segmentos vecinos a través de las fuerzas ejercidas por las presiones de aire altas y bajas alternas. ^[15] Se pueden escribir ecuaciones similares a las de la onda en una cuerda para el cambio en la presión Δ p debido a una onda que viaja hacia la derecha o hacia la izquierda en la tubería.

${\displaystyle \Delta p_{\text{R}}(x,t)=p_{\text{max}}\sin \left({2\pi x \over \lambda }-\omega t\right),}$

${\displaystyle \Delta p_{\text{L}}(x,t)=p_{\text{max}}\sin \left({2\pi x \over \lambda }+\omega t\right),}$

dónde

• p _max es la amplitud de presión o el aumento o disminución máxima de la presión del aire debido a cada onda,
• ω es la frecuencia angular o equivalentemente 2π veces la frecuencia f ,
• λ es la longitud de onda de la onda.

Si ondas idénticas que viajan hacia la derecha y hacia la izquierda viajan a través de la tubería, la superposición resultante se describe mediante la suma

${\displaystyle \Delta p(x,t)=\Delta p_{\text{R}}(x,t)+\Delta p_{\text{L}}(x,t)=2p_{\text{max}}\sin \left({2\pi x \over \lambda }\right)\cos(\omega t).}$

Esta fórmula para la presión tiene la misma forma que la ecuación ( 1 ), por lo que se forma una onda de presión estacionaria que está fija en el espacio y oscila en el tiempo.

Si el extremo de una tubería está cerrado, la presión es máxima, ya que el extremo cerrado de la tubería ejerce una fuerza que restringe el movimiento del aire. Esto corresponde a un antinodo de presión (que es un nodo para los movimientos moleculares, porque las moléculas cerca del extremo cerrado no pueden moverse). Si el extremo de la tubería está abierto, las variaciones de presión son muy pequeñas, lo que corresponde a un nodo de presión (que es un antinodo para los movimientos moleculares, porque las moléculas cerca del extremo abierto pueden moverse libremente). ^{[16] [17]} La ​​ubicación exacta del nodo de presión en un extremo abierto está en realidad ligeramente más allá del extremo abierto de la tubería, por lo que la longitud efectiva de la tubería para el propósito de determinar las frecuencias de resonancia es ligeramente más larga que su longitud física. ^[18] Esta diferencia de longitud se ignora en este ejemplo. En términos de reflexiones, los extremos abiertos reflejan parcialmente las ondas de regreso a la tubería, lo que permite que se libere algo de energía al aire exterior. Idealmente, los extremos cerrados reflejan la onda completa en la otra dirección. ^{[18] [19]}

Consideremos primero un tubo que está abierto en ambos extremos, por ejemplo, un tubo de órgano abierto o una flauta dulce . Dado que la presión debe ser cero en ambos extremos abiertos, las condiciones de contorno son análogas a la cuerda con dos extremos fijos,

${\displaystyle \Delta p(0,t)=0,}$

${\displaystyle \Delta p(L,t)=2p_{\text{max}}\sin \left({2\pi L \over \lambda }\right)\cos(\omega t)=0,}$

que sólo ocurre cuando la longitud de onda de las ondas estacionarias es ^[18]

${\displaystyle \lambda ={\frac {2L}{n}},}$

${\displaystyle n=1,2,3,\ldots ,}$

o equivalentemente cuando la frecuencia es ^{[18] [20]}

${\displaystyle f={\frac {nv}{2L}},}$

donde v es la velocidad del sonido .

A continuación, considere una tubería que está abierta en x = 0 (y por lo tanto tiene un nodo de presión) y cerrada en x = L (y por lo tanto tiene un antinodo de presión). La condición de contorno de "extremo libre" cerrado para la presión en x = L se puede expresar como ∂(Δp)/∂x = 0 , que tiene la forma de la formulación de Sturm–Liouville . La intuición para esta condición de contorno ∂(Δp)/∂x = 0 en x = L es que la presión del extremo cerrado seguirá la del punto a su izquierda. Ejemplos de esta configuración incluyen una botella y un clarinete . Esta tubería tiene condiciones de contorno análogas a la cuerda con un solo extremo fijo. Sus ondas estacionarias tienen longitudes de onda restringidas a ^[18]

${\displaystyle \lambda ={\frac {4L}{n}},}$

${\displaystyle n=1,3,5,\ldots ,}$

o equivalentemente la frecuencia de las ondas estacionarias está restringida a ^{[21] [20]}

${\displaystyle f={\frac {nv}{4L}}.}$

Para el caso en que un extremo está cerrado, n solo toma valores impares, tal como en el caso de la cadena fija en un solo extremo.

Representación molecular de una onda estacionaria con n = 2 para una tubería cerrada en ambos extremos. Considerando el desplazamiento longitudinal, las moléculas en los extremos y las moléculas en el medio no son desplazadas por la onda, lo que representa nodos de desplazamiento longitudinal. A medio camino entre los nodos hay antinodos de desplazamiento longitudinal donde las moléculas son desplazadas al máximo. Considerando la presión, las moléculas son comprimidas y expandidas al máximo en los extremos y en el medio, lo que representa antinodos de presión. A medio camino entre los antinodos hay nodos de presión donde las moléculas no son comprimidas ni expandidas a medida que se mueven.

Hasta ahora, la onda se ha escrito en términos de su presión como función de la posición x y el tiempo. Alternativamente, la onda se puede escribir en términos de su desplazamiento longitudinal del aire, donde el aire en un segmento de la tubería se mueve hacia atrás y hacia adelante ligeramente en la dirección x a medida que varía la presión y las ondas viajan en una o ambas direcciones. El cambio en la presión Δ p y el desplazamiento longitudinal s están relacionados como ^[22]

${\displaystyle \Delta p=-\rho v^{2}{\frac {\partial s}{\partial x}},}$

donde ρ es la densidad del aire. En términos de desplazamiento longitudinal, los extremos cerrados de las tuberías corresponden a nodos ya que el movimiento del aire está restringido y los extremos abiertos corresponden a antinodos ya que el aire es libre de moverse. ^{[18] [23]} Un fenómeno similar, más fácil de visualizar, ocurre en las ondas longitudinales que se propagan a lo largo de un resorte. ^[24]

También podemos considerar una tubería que está cerrada en ambos extremos. En este caso, ambos extremos serán antinodos de presión o, equivalentemente, ambos extremos serán nodos de desplazamiento. Este ejemplo es análogo al caso en el que ambos extremos están abiertos, excepto que el patrón de onda estacionaria tiene un desplazamiento de fase de π ⁄ 2 a lo largo de la dirección x para desplazar la ubicación de los nodos y antinodos. Por ejemplo, la longitud de onda más larga que resuena (el modo fundamental) es nuevamente el doble de la longitud de la tubería, excepto que los extremos de la tubería tienen antinodos de presión en lugar de nodos de presión. Entre los extremos hay un nodo de presión. En el caso de dos extremos cerrados, la longitud de onda nuevamente está restringida a

${\displaystyle \lambda ={\frac {2L}{n}},}$

${\displaystyle n=1,2,3,\ldots ,}$

y la frecuencia se restringe nuevamente a

${\displaystyle f={\frac {nv}{2L}}.}$

Un tubo de Rubens proporciona una forma de visualizar las variaciones de presión de las ondas estacionarias en un tubo con dos extremos cerrados. ^[25]

Onda estacionaria 2D con un límite rectangular

A continuación, considere las ondas transversales que pueden moverse a lo largo de una superficie bidimensional dentro de un límite rectangular de longitud L _x en la dirección x y longitud L _y en la dirección y . Ejemplos de este tipo de onda son las ondas de agua en una piscina o las ondas en una lámina rectangular que se ha tensado. Las ondas desplazan la superficie en la dirección z , donde z = 0 se define como la altura de la superficie cuando está quieta.

En dos dimensiones y coordenadas cartesianas, la ecuación de onda es

${\displaystyle {\frac {\partial ^{2}z}{\partial t^{2}}}\;=\;c^{2}\left({\frac {\partial ^{2}z}{\partial x^{2}}}+{\frac {\partial ^{2}z}{\partial y^{2}}}\right),}$

dónde

• z ( x , y , t ) es el desplazamiento de la superficie,
• c es la velocidad de la onda.

Para resolver esta ecuación diferencial, primero resolvamos su transformada de Fourier , con

${\displaystyle Z(x,y,\omega )=\int _{-\infty }^{\infty }z(x,y,t)e^{-i\omega t}dt.}$

Tomando la transformada de Fourier de la ecuación de onda,

${\displaystyle {\frac {\partial ^{2}Z}{\partial x^{2}}}+{\frac {\partial ^{2}Z}{\partial y^{2}}}=-{\frac {\omega ^{2}}{c^{2}}}Z(x,y,\omega ).}$

Este es un problema de valores propios donde las frecuencias corresponden a valores propios que a su vez corresponden a modos específicos de frecuencia o funciones propias. Específicamente, esta es una forma de la ecuación de Helmholtz y se puede resolver mediante la separación de variables . ^[26] Supongamos

${\displaystyle Z=X(x)Y(y).}$

Dividiendo la ecuación de Helmholtz por Z ,

${\displaystyle {\frac {1}{X(x)}}{\frac {\partial ^{2}X}{\partial x^{2}}}+{\frac {1}{Y(y)}}{\frac {\partial ^{2}Y}{\partial y^{2}}}+{\frac {\omega ^{2}}{c^{2}}}=0.}$

Esto conduce a dos ecuaciones diferenciales ordinarias acopladas. El término x es igual a una constante con respecto a x que podemos definir como

${\displaystyle {\frac {1}{X(x)}}{\frac {\partial ^{2}X}{\partial x^{2}}}=(ik_{x})^{2}.}$

Resolviendo para X ( x ),

${\displaystyle X(x)=A_{k_{x}}e^{ik_{x}x}+B_{k_{x}}e^{-ik_{x}x}.}$

Esta dependencia de x es sinusoidal (recordando la fórmula de Euler) , con constantes A _{k x} y B _{k x} determinadas por las condiciones de contorno. Asimismo, el término y es igual a una constante con respecto a y que podemos definir como

${\displaystyle {\frac {1}{Y(y)}}{\frac {\partial ^{2}Y}{\partial y^{2}}}=(ik_{y})^{2}=k_{x}^{2}-{\frac {\omega ^{2}}{c^{2}}},}$

y la relación de dispersión para esta onda es por lo tanto

${\displaystyle \omega =c{\sqrt {k_{x}^{2}+k_{y}^{2}}}.}$

Resolviendo la ecuación diferencial para el término y ,

${\displaystyle Y(y)=C_{k_{y}}e^{ik_{y}y}+D_{k_{y}}e^{-ik_{y}y}.}$

Al multiplicar estas funciones entre sí y aplicar la transformada de Fourier inversa, z ( x , y , t ) es una superposición de modos donde cada modo es el producto de funciones sinusoidales para x , y y t .

${\displaystyle z(x,y,t)\sim e^{\pm ik_{x}x}e^{\pm ik_{y}y}e^{\pm i\omega t}.}$

Las constantes que determinan las funciones sinusoidales exactas dependen de las condiciones de contorno y de las condiciones iniciales. Para ver cómo se aplican las condiciones de contorno, considere un ejemplo como la hoja que se ha tensado donde z ( x , y , t ) debe ser cero en todo el contorno rectangular. Para la dependencia de x , z ( x , y , t ) debe variar de manera que pueda ser cero tanto en x = 0 como en x = L _x para todos los valores de y y t . Como en el ejemplo unidimensional de la cuerda fija en ambos extremos, la función sinusoidal que satisface esta condición de contorno es

${\displaystyle \sin {k_{x}x},}$

con k _x restringido a

${\displaystyle k_{x}={\frac {n\pi }{L_{x}}},\quad n=1,2,3,\dots }$

De la misma manera, la dependencia y de z ( x , y , t ) debe ser cero tanto en y = 0 como en y = L _y , lo cual se satisface mediante

${\displaystyle \sin {k_{y}y},\quad k_{y}={\frac {m\pi }{L_{y}}},\quad m=1,2,3,\dots }$

Restringir los números de onda a estos valores también restringe las frecuencias que resuenan.

${\displaystyle \omega =c\pi {\sqrt {\left({\frac {n}{L_{x}}}\right)^{2}+\left({\frac {m}{L_{y}}}\right)^{2}}}.}$

Si las condiciones iniciales para z ( x , y ,0) y su derivada temporal ż ( x , y ,0) se eligen de modo que la dependencia t sea una función coseno, entonces las ondas estacionarias para este sistema toman la forma

${\displaystyle z(x,y,t)=z_{\text{max}}\sin \left({\frac {n\pi x}{L_{x}}}\right)\sin \left({\frac {m\pi y}{L_{y}}}\right)\cos \left(\omega t\right).}$

${\displaystyle n=1,2,3,\dots \quad m=1,2,3,\dots }$

Por lo tanto, las ondas estacionarias dentro de este límite rectangular fijo oscilan en el tiempo a ciertas frecuencias resonantes parametrizadas por los números enteros n y m . Como oscilan en el tiempo, no se desplazan y su variación espacial es sinusoidal tanto en la dirección x como en la y, de modo que satisfacen las condiciones de contorno. El modo fundamental, n = 1 y m = 1 , tiene un único antinodo en el medio del rectángulo. Al variar n y m se obtienen patrones bidimensionales complicados pero predecibles de nodos y antinodos dentro del rectángulo. ^[27]

A partir de la relación de dispersión, en ciertas situaciones, diferentes modos (es decir, diferentes combinaciones de n y m) pueden resonar a la misma frecuencia aunque tengan formas diferentes para su dependencia de x e y . Por ejemplo, si el límite es cuadrado, L _x = L _y , los modos n = 1 y m = 7 , n = 7 y m = 1 , y n = 5 y m = 5 resuenan todos a

${\displaystyle \omega ={\frac {c\pi }{L_{x}}}{\sqrt {50}}.}$

Recordando que ω determina el valor propio en la ecuación de Helmholtz anterior, el número de modos correspondientes a cada frecuencia se relaciona con la multiplicidad de la frecuencia como un valor propio.

Relación de ondas estacionarias, fase y transferencia de energía

Si las dos ondas viajeras que se mueven en direcciones opuestas no tienen la misma amplitud, no se cancelarán completamente en los nodos, los puntos donde las ondas están desfasadas 180°, por lo que la amplitud de la onda estacionaria no será cero en los nodos, sino simplemente mínima. La relación de ondas estacionarias (SWR) es la relación entre la amplitud en el antinodo (máxima) y la amplitud en el nodo (mínima). Una onda estacionaria pura tendrá una SWR infinita. También tendrá una fase constante en cualquier punto del espacio (pero puede sufrir una inversión de 180° cada medio ciclo). Una SWR finita, distinta de cero, indica una onda que es parcialmente estacionaria y parcialmente viajera. Tales ondas se pueden descomponer en una superposición de dos ondas: un componente de onda viajera y un componente de onda estacionaria. Una SWR de uno indica que la onda no tiene un componente estacionario; es puramente una onda viajera, ya que la relación de amplitudes es igual a 1. ^[28]

Una onda estacionaria pura no transfiere energía desde la fuente al destino. ^[29] Sin embargo, la onda sigue estando sujeta a pérdidas en el medio. Dichas pérdidas se manifestarán como una ROE finita, lo que indica que un componente de onda viajera sale de la fuente para suplir las pérdidas. Aunque la ROE ahora es finita, todavía puede darse el caso de que ninguna energía llegue al destino porque el componente viajero está puramente supliendo las pérdidas. Sin embargo, en un medio sin pérdidas, una ROE finita implica una transferencia definida de energía al destino.

Ejemplos

Un ejemplo fácil de entender las ondas estacionarias es el de dos personas que sacuden los extremos de una cuerda para saltar . Si lo hacen al mismo tiempo, la cuerda puede formar un patrón regular de ondas que oscilan hacia arriba y hacia abajo, con puntos estacionarios a lo largo de la cuerda donde esta está casi quieta (nodos) y puntos donde el arco de la cuerda es máximo (antinodos).

Resonancia acústica

Inicialmente se pensó que la formación de nubes hexagonales en el polo norte de Saturno se debía a ondas estacionarias de Rossby . ^[30] Sin embargo, esta explicación ha sido cuestionada recientemente. ^[31]

Las ondas estacionarias también se observan en medios físicos como cuerdas y columnas de aire. Cualquier onda que viaja a lo largo del medio se reflejará de vuelta cuando llegue al final. Este efecto es más notorio en los instrumentos musicales donde, en varios múltiplos de la frecuencia natural de una cuerda vibrante o una columna de aire , se crea una onda estacionaria, lo que permite identificar armónicos . Los nodos se producen en los extremos fijos y los antinodos en los extremos abiertos. Si se fija en un solo extremo, solo están disponibles los armónicos impares. En el extremo abierto de una tubería, el antinodo no estará exactamente en el extremo, ya que se altera por su contacto con el aire y, por lo tanto, se utiliza la corrección de extremo para colocarlo exactamente. La densidad de una cuerda afectará la frecuencia a la que se producirán los armónicos; cuanto mayor sea la densidad, menor debe ser la frecuencia para producir una onda estacionaria del mismo armónico.

Luz visible

Las ondas estacionarias también se observan en medios ópticos como guías de ondas ópticas y cavidades ópticas . Los láseres utilizan cavidades ópticas en forma de un par de espejos enfrentados, que constituyen un interferómetro Fabry-Pérot . El medio de ganancia en la cavidad (como un cristal ) emite luz de manera coherente , excitando ondas estacionarias de luz en la cavidad. ^[32] La longitud de onda de la luz es muy corta (en el rango de nanómetros , 10 ⁻⁹ m), por lo que las ondas estacionarias son de tamaño microscópico. Un uso para las ondas de luz estacionarias es medir distancias pequeñas, utilizando planos ópticos .

Rayos X

La interferencia entre haces de rayos X puede formar un campo de ondas estacionarias de rayos X (XSW). ^[33] Debido a la corta longitud de onda de los rayos X (menos de 1 nanómetro), este fenómeno se puede explotar para medir eventos a escala atómica en superficies de materiales . La XSW se genera en la región donde un haz de rayos X interfiere con un haz difractado de una superficie de monocristal casi perfecta o un reflejo de un espejo de rayos X. Al ajustar la geometría del cristal o la longitud de onda de los rayos X, la XSW se puede trasladar en el espacio, lo que provoca un cambio en la fluorescencia de rayos X o el rendimiento de fotoelectrones de los átomos cerca de la superficie. Este cambio se puede analizar para señalar la ubicación de una especie atómica particular en relación con la estructura cristalina subyacente o la superficie del espejo. El método XSW se ha utilizado para aclarar los detalles a escala atómica de los dopantes en semiconductores, ^[34] la adsorción atómica y molecular en superficies, ^[35] y las transformaciones químicas involucradas en la catálisis . ^[36]

Ondas mecánicas

Las ondas estacionarias se pueden inducir mecánicamente en un medio sólido mediante resonancia. Un ejemplo fácil de entender es el de dos personas que sacuden cada extremo de una cuerda para saltar. Si se sacuden en sincronía, la cuerda formará un patrón regular con nodos y antinodos y parecerá estacionaria, de ahí el nombre de onda estacionaria. De manera similar, se puede imponer una onda estacionaria sobre una viga en voladizo mediante la aplicación de una excitación de base. En este caso, el extremo libre se mueve la mayor distancia lateralmente en comparación con cualquier ubicación a lo largo de la viga. Un dispositivo de este tipo se puede utilizar como sensor para rastrear cambios en la frecuencia o fase de la resonancia de la fibra. Una aplicación es como dispositivo de medición para metrología dimensional . ^{[37] [38]}

Ondas sísmicas

Las ondas superficiales estacionarias en la Tierra se observan como oscilaciones libres de la Tierra .

Ondas de Faraday

La onda de Faraday es una onda estacionaria no lineal en la interfaz aire-líquido inducida por la inestabilidad hidrodinámica. Puede utilizarse como plantilla líquida para ensamblar materiales a microescala. ^[39]

Seiches

Una seiche es un ejemplo de onda estacionaria en un cuerpo de agua cerrado. Se caracteriza por el comportamiento oscilatorio del nivel del agua en cada extremo del cuerpo y, por lo general, tiene un punto nodal cerca del centro del cuerpo donde se observa muy poco cambio en el nivel del agua. Debe distinguirse de una simple marejada ciclónica donde no hay oscilación presente. En lagos de gran tamaño, el período de tales oscilaciones puede ser de entre minutos y horas, por ejemplo, el período longitudinal del lago de Ginebra es de 73 minutos y su seiche transversal tiene un período de alrededor de 10 minutos, ^[40] mientras que se puede observar que el lago Huron tiene resonancias con períodos de entre 1 y 2 horas. ^[41] Véase Seiches de lagos . ^{[42] [43] [44]}

Véase también

Ondas

• Índice de artículos sobre olas :
• Punto anfidrómico
• Clapotis
• Modo longitudinal
• Bloqueo de modo
• Ritmo metacrónico
• Modos de sala resonante
• Seiche
• Trompeta
• El tubo de Kundt
• Ecuación de onda

Electrónica

• Índice de artículos de electrónica :
• Resonador de cavidad
• Impedancia característica
• Cimática
• Impedancia
• Modo normal

Notas

1. Alwyn Scott (ed), Enciclopedia de ciencia no lineal , pág. 683, Routledge, 2006 ISBN  1135455589 .
2. Theodore Y. Wu, "Estabilidad de ondas no lineales sostenidas resonantemente", Inestabilidad no lineal de flujos no paralelos: Simposio IUTAM Potsdam, Nueva York , pág. 368, Springer, 2012 ISBN 3642850847 . 
3. Melde, Franz. Ueber einige krumme Flächen, welche von Ebenen, paralelo einer bestimmten Ebene, durchschnitten, als Durchschnittsfigur einen Kegelschnitt liefern: Disertación inaugural... Koch, 1859.
4. Melde, Franz. "Ueber die Erregung stehender Wellen eines fadenförmigen Körpers." Annalen der Physik 185, núm. 2 (1860): 193–215.
5. Melde, Franz. Die Lehre von den Schwingungscurven...: mit einem Atlas von 11 Tafeln in Steindruck. JA Barth, 1864.
6. Melde, Franz. "Akustische Experimentaluntersuchungen". Annalen der Physik 257, núm. 3 (1884): 452–470.
7. Dietsche, Daniela (31 de diciembre de 2014). "Surfbare Wechselsprünge | Espazium". www.espazium.ch (en alemán) . Consultado el 13 de enero de 2022 .
8.  Este artículo incorpora material de dominio público de la Norma Federal 1037C. Administración de Servicios Generales . Archivado desde el original el 22 de enero de 2022.
9. Blackstock, David T. (2000), Fundamentos de acústica física , Wiley–IEEE, pág. 141, ISBN 0-471-31979-1
10. Halliday, Resnick y Walker 2005, pág. 432.
11. Halliday, Resnick y Walker 2005, pág. 434.
12. Serway y Faughn 1992, pág. 472.
13. Serway y Faughn 1992, págs. 475-476.
14. Resonancia de cuerdas. Sonido y música digital. 21 de mayo de 2014. ID de video de YouTube: oZ38Y0K8e-Y . Consultado el 22 de agosto de 2020 .
15. Halliday, Resnick y Walker 2005, pág. 450.
16. Nave, CR (2016). "Ondas estacionarias". HyperPhysics. Universidad Estatal de Georgia . Consultado el 23 de agosto de 2020 .
17. Calles 2010, pág. 6.
18. Halliday, Resnick y Walker 2005, pág. 457.
19. Calles 2010, pág. 15.
20. Serway y Faughn 1992, pág. 478.
21. Halliday, Resnick y Walker 2005, pág. 458.
22. Halliday, Resnick y Walker 2005, pág. 451.
23. Serway y Faughn 1992, pág. 477.
24. Thomas-Palmer, Jonathan (16 de octubre de 2019). Demostración de ondas estacionarias longitudinales. Física de volteos. El evento ocurre en 4:11. ID de video de YouTube: 3QbmvunlQR0 . Consultado el 23 de agosto de 2020 .
25. Mould, Steve (13 de abril de 2017). Una mejor descripción de la resonancia. YouTube. El evento ocurre a las 6:04. ID del video de YouTube: dihQuwrf9yQ . Consultado el 23 de agosto de 2020 .
26. Weisstein, Eric W. "Ecuación diferencial de Helmholtz: coordenadas cartesianas". MathWorld: un recurso web de Wolfram . Consultado el 2 de enero de 2021 .
27. Gallis, Michael R. (15 de febrero de 2008). Patrones de ondas estacionarias en 2D (límites fijos rectangulares). Animaciones para física y astronomía. Universidad Estatal de Pensilvania. También disponible como ID de video de YouTube: NMlys8A0_4s . Consultado el 28 de diciembre de 2020 .
28. RS Rao, Ingeniería de microondas , págs. 153-154, PHI Learning, 2015 ISBN 8120351592 . 
29. KA Tsokos, Física para el Diploma del IB , p. 251, Cambridge University Press, 2010 ISBN 0521138213 . 
30. Una interpretación dinámica de ondas de la región polar de Saturno Archivado el 21 de octubre de 2011 en Wayback Machine , M. Allison, DA Godfrey, RF Beebe, Science vol. 247, pág. 1061 (1990)
31. Barbosa Aguiar, Ana C. (2010). "Un modelo de laboratorio del hexágono polar norte de Saturno". Icarus . 206 (2): 755–763. Bibcode :2010Icar..206..755B. doi :10.1016/j.icarus.2009.10.022.
32. Pedrotti, Frank L.; Pedrotti, Leno M. (2017). Introducción a la óptica (3.ª ed.). Cambridge University Press . ISBN 978-1-108-42826-2.
33. Batterman, Boris W.; Cole, Henderson (1964). "Difracción dinámica de rayos X por cristales perfectos". Reseñas de Física Moderna . 36 (3): 681–717. Bibcode :1964RvMP...36..681B. doi :10.1103/RevModPhys.36.681.
34. Batterman, Boris W. (1969). "Detección de sitios de átomos extraños por su dispersión de fluorescencia de rayos X". Physical Review Letters . 22 (14): 703–705. Código Bibliográfico :1969PhRvL..22..703B. doi :10.1103/PhysRevLett.22.703.
35. Golovchenko, JA; Patel, JR; Kaplan, DR; Cowan, PL; Bedzyk, MJ (1982). "Solución al problema de registro de superficies utilizando ondas estacionarias de rayos X" (PDF) . Physical Review Letters . 49 (8): 560–563. Bibcode :1982PhRvL..49..560G. doi :10.1103/PhysRevLett.49.560.
36. Feng, Z.; Kim, C.-Y.; Elam, JW; Ma, Q.; Zhang, Z.; Bedzyk, MJ (2009). "Observación directa a escala atómica de la dinámica de cationes inducida por rédox en un catalizador monocapa soportado por óxido: WO _x /α-Fe ₂ O ₃ (0001)". J. Am. Chem. Soc . 131 (51): 18200–18201. doi :10.1021/ja906816y. PMID  20028144.
37. Bauza, Marcin B.; Hocken, Robert J.; Smith, Stuart T.; Woody, Shane C. (2005). "Desarrollo de una punta de sonda virtual con una aplicación a características de microescala de alta relación de aspecto". Review of Scientific Instruments . 76 (9): 095112–095112–8. Bibcode :2005RScI...76i5112B. doi :10.1063/1.2052027.
38. "Ingeniería de precisión y soluciones de fabricación – IST Precision". www.insitutec.com . Archivado desde el original el 31 de julio de 2016 . Consultado el 28 de abril de 2018 .
39. Chen, Pu (2014). "Ensamblaje a microescala dirigido por plantilla basada en líquido". Materiales avanzados . 26 (34): 5936–5941. doi :10.1002/adma.201402079. PMC 4159433 . PMID  24956442. 
40. Lemmin, Ulrich (2012), "Seiches superficiales", en Bengtsson, Lars; Herschy, Reginald W.; Fairbridge, Rhodes W. (eds.), Enciclopedia de lagos y embalses , Enciclopedia de ciencias de la Tierra, Springer Países Bajos, págs. 751–753, doi :10.1007/978-1-4020-4410-6_226, ISBN 978-1-4020-4410-6
41. "Marejada ciclónica en el lago Hurón el 13 de julio de 1995". NOAA. Archivado desde el original el 16 de septiembre de 2008. Consultado el 1 de enero de 2023 .
42. Korgen, Ben (febrero de 2000). "Bonanza para el lago Superior: los seiches hacen más que mover agua". seagrant.umn.edu . Universidad de Minnesota Duluth . Archivado desde el original el 27 de diciembre de 2007.
43. "Seiche". www.soest.hawaii.edu . Archivado desde el original el 26 de enero de 2019 . Consultado el 1 de enero de 2023 .
44. Johnson, Scott K. (30 de junio de 2013). «Un terremoto en Japón literalmente provocó olas en Noruega». Ars Technica . Archivado desde el original el 30 de julio de 2022. Consultado el 1 de enero de 2023 .

Referencias

• Halliday, David; Resnick, Robert; Walker, Jearl (2005). Fundamentos de física (7.ª ed.). John Wiley & Sons. ISBN 0-471-42959-7.
• Serway, Raymond A.; Faughn, Jerry S. (1992). Física universitaria (3.ª ed.). Saunders College Publishing. ISBN 0-03-076377-0.
• Streets, J. (2010). "Capítulo 16 – Superposición y ondas estacionarias" (PDF) . Departamento de Física. PHYS122 Fundamentos de Física II. Universidad de Maryland . Consultado el 23 de agosto de 2020 .

Enlaces externos

• Medios relacionados con Ondas estacionarias en Wikimedia Commons