Ley de Titius-Bode

Hipótesis desacreditada sobre las órbitas de los planetas del Sistema Solar

La ley de Titius-Bode (a veces denominada simplemente ley de Bode ) es una predicción formularia de la distancia entre los planetas en cualquier sistema planetario dado . La fórmula sugiere que, extendiéndose hacia afuera, cada planeta debería estar aproximadamente al doble de distancia del Sol que el anterior. La hipótesis anticipó correctamente las órbitas de Ceres (en el cinturón de asteroides ) y Urano , pero falló como predictor de la órbita de Neptuno . Lleva el nombre de Johann Daniel Titius y Johann Elert Bode .

Trabajos posteriores de Mary Adela Blagg y DE Richardson revisaron significativamente la fórmula original y realizaron predicciones que fueron validadas posteriormente por nuevos descubrimientos y observaciones. Son estas reformulaciones las que ofrecen "las mejores representaciones fenomenológicas de las distancias con las que investigar el significado teórico de las leyes de tipo Titius-Bode". ^[1]

Formulación original

La ley relaciona el semieje mayor de cada planeta hacia afuera del Sol en unidades tales que el semieje mayor de la Tierra es igual a 10: ${\displaystyle ~a_{n}~}$

${\displaystyle ~a=4+x~}$

donde tal que, con excepción del primer paso, cada valor es el doble del valor anterior. Existe otra representación de la fórmula: ${\displaystyle ~x=0,3,6,12,24,48,96,192,384,768\ldots ~}$

${\displaystyle ~a=4+3\times 2^{n}~}$

donde Los valores resultantes se pueden dividir por 10 para convertirlos en unidades astronómicas ( AU ), dando como resultado la expresión: ${\displaystyle ~n=-\infty ,0,1,2,\ldots ~.}$

${\displaystyle a=0.4+0.3\times 2^{n}~.}$

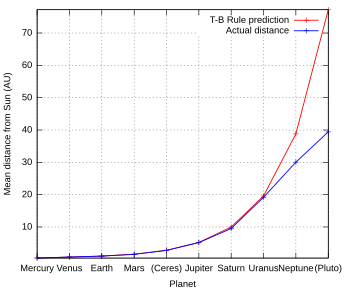
En el caso de los planetas más alejados, más allá de Saturno , se predice que cada planeta estará aproximadamente al doble de distancia del Sol que el objeto anterior. Mientras que la ley de Titius-Bode predice que Saturno , Urano , Neptuno y Plutón se encuentran aproximadamente a 10, 20, 39 y 77  UA , los valores reales están más cerca de 10, 19, 30 y 40  UA . ^[a]

Origen e historia

Juan Daniel Ticio (1729-1796)

Johann Elert Bode (1747-1826)

La primera mención de una serie que se aproxima a la ley de Bode se encuentra en un libro de texto de D. Gregory (1715): ^[2]

"... suponiendo que la distancia de la Tierra al Sol se divida en diez partes iguales, de éstas la distancia de Mercurio será unas cuatro, la de Venus siete, la de Marte quince, la de Júpiter cincuenta y dos y la de Saturno noventa y cinco." ^[3]

Una frase similar, probablemente parafraseada de Gregory (1715), ^{[2] [3]} aparece en una obra publicada por C. Wolff en 1724.

En 1764, C. Bonnet escribió: ^[4]

“Conocemos diecisiete planetas [es decir, los planetas mayores y sus satélites] que entran en la composición de nuestro sistema solar; pero no estamos seguros de que no haya más.” ^{[4] [3]}

En su traducción de la obra de Bonnet de 1766, J. D. Titius añadió dos párrafos propios a la declaración anterior. Las inserciones se colocaron en la parte inferior de la página 7 y en la parte superior de la página 8. El nuevo párrafo no se encuentra en el texto original en francés de Bonnet ni en las traducciones de la obra al italiano y al inglés.

El texto insertado por Titius consta de dos partes. La primera explica la sucesión de distancias planetarias al Sol:

Observad las distancias de los planetas entre sí y reconoced que casi todos están separados entre sí en una proporción que corresponde a sus magnitudes corporales. Dividid la distancia del Sol a Saturno en 100 partes; Mercurio está separado del Sol por cuatro de esas partes, Venus por 4+3=7 de esas partes, la Tierra por 4+6=10, Marte por 4+12=16. Pero observad que de Marte a Júpiter hay una desviación de esta progresión tan exacta. De Marte sigue un espacio de 4+24=28 de esas partes, pero hasta ahora no se ha avistado allí ningún planeta. Pero ¿debía el Señor Arquitecto haber dejado vacío ese espacio? De ningún modo. Supongamos, pues, que este espacio pertenece sin duda a los satélites de Marte aún no descubiertos, añadamos también que quizá Júpiter tenga todavía alrededor de sí algunos más pequeños que no han sido avistados todavía por ningún telescopio. Junto a este espacio aún inexplorado para nosotros se eleva la esfera de influencia de Júpiter en 4+48=52 partes; y la de Saturno en 4+96=100 partes. ^{[ cita requerida ]}

En 1772, JE Bode , que entonces tenía veinticinco años, publicó un compendio astronómico, ^[5] en el que incluyó la siguiente nota a pie de página, citando a Titius (en ediciones posteriores): ^{[b] [6]}

Este último punto parece deducirse, en particular, de la asombrosa relación que guardan los seis planetas conocidos en sus distancias al Sol. Supongamos que la distancia del Sol a Saturno es de 100, entonces Mercurio está separado del Sol por 4 partes de ese mismo número. Venus está a 4+3=7. La Tierra a 4+6=10. Marte a 4+12=16. Ahora viene una brecha en esta progresión tan ordenada. Después de Marte sigue un espacio de 4+24=28 partes, en el que todavía no se ha visto ningún planeta. ¿Puede uno creer que el Fundador del universo haya dejado este espacio vacío? Ciertamente no. De aquí llegamos a la distancia de Júpiter de 4+48=52 partes, y finalmente a la de Saturno de 4+96=100 partes. ^[6]

Estas dos afirmaciones, a pesar de su peculiar expresión y de los radios utilizados para las órbitas, parecen provenir de un antiguo algoritmo de un cosmista . ^[c]

Se encontraron muchos precedentes que datan de antes del siglo XVII. ^{[ cita requerida ]} Titius fue discípulo del filósofo alemán CF von Wolf (1679-1754), y la segunda parte del texto que Titius insertó en la obra de Bonnet se encuentra en un libro de von Wolf (1723), ^[7] lo que sugiere que Titius aprendió la relación de él. La literatura del siglo XX sobre la ley de Titius-Bode atribuye la autoría a von Wolf. ^{[ cita requerida ]} Una versión anterior fue escrita por D. Gregory (1702), ^[8] en la que la sucesión de distancias planetarias 4, 7, 10, 16, 52 y 100 se convirtió en una progresión geométrica con razón 2. Esta es la fórmula newtoniana más cercana, que también fue citada por Benjamin Martin (1747) ^[9] y Tomàs Cerdà (c. 1760) ^[10] años antes de la traducción ampliada de Titius del libro de Bonnet al alemán (1766). Durante los siguientes dos siglos, los autores posteriores continuaron presentando sus propias versiones modificadas, aparentemente sin tener conocimiento de trabajos anteriores. ^[1]

Titius y Bode esperaban que la ley condujera al descubrimiento de nuevos planetas y, de hecho, el descubrimiento de Urano y Ceres (cuyas distancias se ajustan bien a la ley) contribuyó a la fama de la ley. Sin embargo, la distancia de Neptuno era muy discrepante y, de hecho, Plutón (que ya no se considera un planeta) se encuentra a una distancia media que corresponde aproximadamente a la que la ley de Titius-Bode predijo para el próximo planeta a partir de Urano.

Cuando se publicó originalmente, la ley se cumplía aproximadamente con todos los planetas conocidos en ese momento (es decir, desde Mercurio hasta Saturno ), con un espacio entre el cuarto y el quinto planeta. Vikarius (Johann Friedrich) Wurm (1787) propuso una versión modificada de la Ley de Titius-Bode que tenía en cuenta los satélites entonces conocidos de Júpiter y Saturno, y predecía mejor la distancia de Mercurio. ^[11]

La ley de Titius-Bode se consideró interesante, pero sin gran importancia, hasta el descubrimiento de Urano en 1781, que encaja en la serie casi exactamente. Basándose en este descubrimiento, Bode instó a sus contemporáneos a buscar un quinto planeta. Ceres , el objeto más grande del cinturón de asteroides , fue encontrado en la posición predicha por Bode en 1801.

La ley de Bode fue ampliamente aceptada en ese momento, hasta que en 1846 se descubrió a Neptuno en un lugar que no se ajusta a la ley. Al mismo tiempo, debido a la gran cantidad de asteroides descubiertos en el cinturón , Ceres ya no era un planeta importante. En 1898, el astrónomo y lógico CS Peirce utilizó la ley de Bode como un ejemplo de razonamiento falaz. ^[12]

El descubrimiento de Plutón en 1930 complicó aún más la cuestión: aunque no se encontraba en la posición prevista por la ley de Bode, sí se encontraba muy cerca de la posición que la ley había designado para Neptuno. El descubrimiento posterior del cinturón de Kuiper –y en particular del objeto Eris , que es más masivo que Plutón, pero no se ajusta a la ley de Bode– desacreditó aún más la fórmula. ^[13]

Datos

La ley de Titius-Bode predice que habrá planetas a distancias específicas en unidades astronómicas , que pueden compararse con los datos observados para los planetas y dos planetas enanos en el Sistema Solar:

Representación gráfica de los ocho planetas, Plutón y Ceres frente a las diez primeras distancias previstas.

¹ Para un valor de k grande , cada distancia de la regla de Titius-Bode es aproximadamente el doble del valor anterior. Por lo tanto, se puede encontrar un planeta arbitrario dentro del −25% al ​​+50% de una de las posiciones predichas. Para un valor de k pequeño , las distancias predichas no se duplican por completo, por lo que el rango de desviación potencial es menor. Nótese que el semieje mayor es proporcional a la potencia 2/3 del período orbital . Por ejemplo, los planetas en una resonancia orbital 2:3 (como los plutinos en relación con Neptuno ) variarán en distancia en (2/3) ^2/3 = −23,69% y +31,04% en relación entre sí.
² Ceres y Plutón son planetas enanos en lugar de planetas mayores .

Formulación de Blagg

En 1913, MA Blagg , astrónoma de Oxford, revisó la ley. ^[14] Analizó las órbitas del sistema planetario y las de los sistemas de satélites de los gigantes gaseosos exteriores, Júpiter, Saturno y Urano. Examinó el logaritmo de las distancias, tratando de encontrar la mejor diferencia "promedio".

La función de corrección empírica   f   introducida en la reformulación de Blagg de la ley de Titius-Bode.

Su análisis dio como resultado una fórmula diferente:

${\displaystyle \ {\mathsf {distance}}=A\cdot {\bigl [}\ B+f\left(\alpha +n\ \beta \right)\ {\bigr ]}\ {\bigl (}\ 1.7275\ {\bigr )}^{n}~.}$

Obsérvese en particular que en la fórmula de Blagg, la ley del Sistema Solar se representaba mejor mediante una progresión en 1,7275 , en lugar del valor original 2 utilizado por Titius, Bode y otros.

Blagg examinó el sistema de satélites de Júpiter , Saturno y Urano , y descubrió la misma relación de progresión 1,7275 en cada uno.

Sin embargo, la forma final de la función de corrección   f   no se presentó en el artículo de Blagg de 1913, ya que Blagg señaló que las cifras empíricas presentadas eran solo para fines ilustrativos. La forma empírica se proporcionó en forma de gráfico (la razón por la que los puntos de la curva coinciden tanto con los datos empíricos, para los objetos descubiertos antes de 1913, es que son los datos empíricos).

Resultó difícil encontrar una fórmula que se ajustara a la curva empírica. El análisis de Fourier de la forma dio como resultado la siguiente aproximación de siete términos: ^[14]

$${\displaystyle {\begin{aligned}\ f{\bigl (}\ \theta \ {\bigr )}\;=\;0.4594\;+\;\;&0.396\ \cos \!{\bigl (}\ \theta -27.4^{\circ }\ {\bigr )}\;+\;0.168\ \cos \!{\bigl (}\ 2\ (\ \theta -60.4^{\circ })\ {\bigr )}\;+\;0.062\ \cos \!{\bigl (}\ 3\ (\ \theta -28.1^{\circ })\ {\bigr )}\;+\;\\\;+\;\;&0.053\ \cos \!{\bigl (}\ 4\ (\ \theta -77.2^{\circ })\ {\bigr )}\;+\;0.009\ \cos \!{\bigl (}\ 5\ (\ \theta -22^{\circ })\ {\bigr )}\;+\;0.012\ \cos \!{\bigl (}\ 7\ (\ \theta -40.4^{\circ })\ {\bigr )}~.\end{aligned}}}$$

Después de un análisis más profundo, Blagg proporcionó la siguiente fórmula más simple; sin embargo, el precio de la forma más simple es que produce un ajuste menos preciso a los datos empíricos. Blagg la presentó en una forma no normalizada en su artículo, lo que deja ambiguos los tamaños relativos de A , B y f   ; se muestra aquí en forma normalizada (es decir, esta versión de   f   se escala para producir valores que van de 0 a 1 , inclusive): ^[15]

$${\displaystyle \ f{\bigl (}\ \theta \ {\bigr )}\;=\;0.249\;+\;0.860\ \left({\frac {\ \cos \ \Psi \ }{\ 3-\cos \!\left(\ 2\ \Psi \ \right)\ }}\;+\;{\frac {1}{\ 6-4\ \cos \!\left(\ 2\ \Psi -60^{\circ }\right)\ }}\right)\ ,}$$

dónde ${\displaystyle \ \Psi \equiv \theta -27.5^{\circ }~.}$

Ninguna de estas fórmulas para la función   f   se utiliza en los cálculos siguientes: Los cálculos aquí se basan en un gráfico de la función   f   que se dibujó en base a datos observados.

Su artículo fue publicado en 1913, y fue olvidado hasta 1953, cuando AE Roy lo encontró mientras investigaba otro problema. ^[16] Roy señaló que la propia Blagg había sugerido que su fórmula podría dar distancias medias aproximadas de otros cuerpos aún sin descubrir en 1913. Desde entonces, se habían descubierto seis cuerpos en tres sistemas examinados por Blagg: Plutón , Sinope ( Júpiter IX ), Lysithea ( J X ), Carme ( J XI ), Ananke ( J XII ) y Miranda ( Urano V ).

Roy descubrió que los seis cuerpos coincidían perfectamente. Esto podría haber sido una exageración: de estos seis cuerpos, cuatro compartían posiciones con objetos que ya se conocían en 1913; en cuanto a los otros dos, había una sobrestimación de aproximadamente el 6% para Plutón; y más tarde, se hizo evidente una subestimación del 6% para Miranda. ^[15]

Comparación de la formulación de Blagg con la observación

Los cuerpos entre paréntesis no se conocían en 1913, cuando Blagg escribió su artículo. Algunas de las distancias calculadas en los sistemas de Saturno y Urano no son muy precisas. Esto se debe a que los bajos valores de la constante B en la tabla anterior las hacen muy sensibles a la forma exacta de la función   f  .

Formulación de Richardson

En un artículo de la revista Popular Astronomy de 1945 , ^[17] el escritor científico DE Richardson aparentemente llegó de forma independiente a la misma conclusión que Blagg: que la razón de progresión es 1,728 en lugar de 2. Su ley de espaciamiento tiene la forma:

$${\displaystyle \ R_{n}={\bigl (}\ 1.728\ {\bigr )}^{n}\ \varrho _{n}(\theta _{n})\ ,}$$

donde es una función oscilatoria con período , que representa distancias desde un origen descentrado a puntos en una elipse. ${\displaystyle \varrho _{n}}$ ${\displaystyle 2\pi }$ ${\displaystyle \varrho _{n}}$

Inercia histórica

Nieto, quien realizó la primera revisión integral moderna de la Ley de Titius-Bode, ^[18] señaló que "la influencia psicológica de la Ley en la astronomía ha sido tal que la gente siempre ha tendido a considerar su forma original como aquella en la que basar las teorías". Fue enfático en que "las teorías futuras deben librarse del sesgo de intentar explicar una relación de progresión de 2":

Una cosa que debe enfatizarse es que el sesgo histórico hacia una razón de progresión de 2 debe abandonarse . Debe quedar claro que la primera formulación de Titius (con su primer término asimétrico) debe considerarse como una buena primera estimación . Ciertamente, no debe verse necesariamente como la mejor estimación a la que referirse para las teorías. Pero en astronomía el peso de la historia es pesado... A pesar del hecho de que el número 1,73 es mucho mejor, los astrónomos se aferran al número original 2. ^[1]

Explicaciones teóricas

No existe ninguna explicación teórica sólida que sustente la ley de Titius-Bode, pero es posible que, dada una combinación de resonancia orbital y escasez de grados de libertad , cualquier sistema planetario estable tenga una alta probabilidad de satisfacer una relación de tipo Titius-Bode. Dado que puede tratarse de una coincidencia matemática en lugar de una "ley de la naturaleza", a veces se la denomina regla en lugar de "ley". ^[19] El astrofísico Alan Boss afirma que es sólo una coincidencia, y la revista científica planetaria Icarus ya no acepta artículos que intenten proporcionar versiones mejoradas de la "ley". ^[13]

La resonancia orbital de los principales cuerpos en órbita crea regiones alrededor del Sol que están libres de órbitas estables a largo plazo. Los resultados de las simulaciones de formación planetaria respaldan la idea de que un sistema planetario estable elegido al azar probablemente satisfaga una ley de Titius-Bode. ^[20]

Dubrulle y Graner ^{[21] [22]} demostraron que las reglas de distancia de ley de potencia pueden ser una consecuencia de los modelos de nubes colapsantes de sistemas planetarios que poseen dos simetrías: invariancia rotacional (es decir, la nube y su contenido son axialmente simétricos) e invariancia de escala (es decir, la nube y su contenido se ven iguales en todas las escalas). Esta última es una característica de muchos fenómenos que se considera que desempeñan un papel en la formación planetaria, como la turbulencia.

Sistemas de satélites naturales y sistemas exoplanetarios

Sólo hay un número limitado de sistemas disponibles en los que se puede probar actualmente la ley de Bode; dos planetas solares tienen suficientes lunas grandes que probablemente se formaron en un proceso similar al que formó los planetas: los cuatro satélites grandes de Júpiter y el satélite interior más grande (es decir, Amaltea ) se aferran a un espaciado regular, pero no de Titius-Bode, con los cuatro satélites más internos bloqueados en períodos orbitales que son cada uno el doble del siguiente satélite interior. De manera similar, las lunas grandes de Urano tienen un espaciado regular pero no de Titius-Bode. ^[23] Sin embargo, según Martin Harwit

"Una nueva redacción de esta ley nos permite incluir no sólo las órbitas planetarias alrededor del Sol, sino también las órbitas de las lunas alrededor de sus planetas progenitores". ^[24]

La nueva formulación se conoce como “ ley de Dermott ”.

De los recientes descubrimientos de sistemas planetarios extrasolares, pocos tienen suficientes planetas conocidos como para comprobar si se aplican reglas similares. Un intento con 55 Cancri sugirió la ecuación

${\displaystyle ~a_{n}=0.0142\cdot \mathrm {e} ^{\left(\,0.9975\,n\,\right)}=0.0142\cdot {\bigl (}\,2.7115\,{\bigr )}^{n}~,}$

y controvertidamente ^[25] predice un planeta no descubierto o un campo de asteroides para al menos 2  UA . ^[26] Además, el período orbital y el semieje mayor del planeta más interno en el sistema 55 Cancri se han revisado en gran medida (de 2,817 días a 0,737 días y de 0,038  UA a 0,016  UA , respectivamente) desde la publicación de estos estudios. ^[27] ${\displaystyle ~n=5~}$

Investigaciones astronómicas recientes sugieren que los sistemas planetarios alrededor de otras estrellas pueden seguir leyes similares a las de Titius-Bode. ^{[28] [29]} Bovaird y Lineweaver (2013) ^[30] aplicaron una relación generalizada de Titius-Bode a 68 sistemas de exoplanetas que contienen cuatro o más planetas. Demostraron que el 96% de estos sistemas de exoplanetas se adhieren a una relación generalizada de Titius-Bode en un grado similar o mayor que el Sistema Solar. Se predicen las ubicaciones de exoplanetas potencialmente no detectados en cada sistema. ^[30]

Investigaciones posteriores detectaron 5 candidatos a planetas de los 97 planetas predichos para los 68 sistemas planetarios. El estudio mostró que el número real de planetas podría ser mayor. Se desconocen las tasas de aparición de planetas del tamaño de Marte y Mercurio, por lo que muchos planetas podrían pasarse por alto debido a su pequeño tamaño. Otras posibles razones que pueden explicar las aparentes discrepancias incluyen planetas que no transitan la estrella o circunstancias en las que el espacio predicho está ocupado por discos circunestelares . A pesar de este tipo de concesiones, el número de planetas encontrados con las predicciones de la ley de Titius-Bode fue menor de lo esperado. ^[31]

En un artículo de 2018, se propuso la idea de un hipotético octavo planeta alrededor de TRAPPIST-1 llamado "TRAPPIST-1i", utilizando la ley de Titius-Bode. TRAPPIST-1i tenía una predicción basada exclusivamente en la ley de Titius-Bode con un período orbital de 27,53 ± 0,83 días . ^[32]

Finalmente, las estadísticas brutas de las órbitas exoplanetarias apuntan fuertemente a un cumplimiento general de las leyes tipo Titius-Bode (con aumento exponencial de los semiejes mayores en función del índice planetario) en todos los sistemas exoplanetarios; al hacer un histograma ciego de los semiejes mayores orbitales para todos los exoplanetas conocidos para los cuales se conoce esta magnitud, ^[33] y compararlo con lo que debería esperarse si los planetas se distribuyen de acuerdo a las leyes tipo Titius-Bode, se obtiene un grado significativo de acuerdo (es decir, 78%) ^{[34] .}

Véase también

• Ley de Dermott
• Faetón (planeta hipotético)
• Espiral logarítmica
• El potencial de Lennard-Jones
• Misterio cosmográfico

Notas al pie

1. El espaciado parece pasar de la complicada serie de Titius a un espaciado igual simple a partir de Saturno, siendo Neptuno el primer planeta importante que no se ajusta a la regla de Titius-Bode.
2. La nota a pie de página de Bode inicialmente no tenía fuentes, pero en versiones posteriores se le atribuye a Titius, y en las memorias de Bode se refiere a Titius, reconociendo claramente la prioridad de Titius.
3. Los cosistas eran expertos en cálculos de todo tipo y eran empleados por comerciantes y hombres de negocios para resolver problemas contables complejos. Su nombre deriva de la palabra italiana cosa , que significa "cosa", porque utilizaban símbolos para representar una cantidad desconocida, de forma similar a la forma en que los matemáticos modernos utilizan los símbolos. Los solucionadores de problemas profesionales de esta era inventaron sus propios métodos ingeniosos para realizar cálculos y hacían todo lo posible por mantener estos métodos en secreto para mantener la reputación de ser la única persona capaz de resolver un problema en particular. ^{[ cita requerida ]} ${\displaystyle \,x\;.}$

Referencias

1. Nieto, Michael Martin (1970). "Conclusiones sobre la ley de Titius-Bode de las distancias planetarias". Astron. Astrophys . 8 : 105–111. Bibcode :1970A&A.....8..105N.
2. Gregory, D. (1715). Los elementos de la astronomía .
3. "¿Dónde deberían estar los planetas? La ley de proporcionalidades". Amanecer. Archivado desde el original el 7 de marzo de 2016 . Consultado el 16 de marzo de 2018 .
4. Bonnet, C. (1764). Contemplación de la naturaleza (en francés).
5. Bode, Johann Elert (1772). Anleitung zur Kenntniss des gestirnten Himmels [ Manual para conocer el cielo estrellado ] (en alemán) (2ª ed.).
6. Hoskin, Michael (26 de junio de 1992). «La ley de Bodes y el descubrimiento de Ceres». Observatorio Astronomico di Palermo «Giuseppe S. Vaiana» . Consultado el 5 de julio de 2007 .
7. von Wolf, CF (1723). Vernünftige Gedanken von den Wirkungen der Natur (en alemán).
8. Gregorio, David (1702). Astronomiae physicae et geométricae elementa (en latín).
9. Martín, Benjamín (1747). Filosofía Británica .
10. Cerdà, Tomás (hacia 1760). Tratado de Astronomía (en español).
11. Sierpe, Vikarius (Johann Friedrich) (1787). Bode, JE (ed.). "Verschiedene astronomische Bemerkungen und eine Abhandlung über mögliche Planeten und Kometen unsers Sonnensystems". Astronomisches Jahrbuch . 15 . Hofbuchdrucker, Berlín: George Jacob Decker, Königl: 162–73.
12. Peirce, CS ; Ketner, Kenneth Laine (1992). Razonamiento y lógica de las cosas. Las conferencias de Cambridge de 1898. Harvard University Press . pp. 194–196. ISBN 978-0-674-74966-5.Página del catálogo HUP Archivado el 2 de enero de 2010 en Wayback Machine .
13. Boss, Alan (octubre de 2006). "Pregúntale a Astro". Astronomía . Vol. 30, núm. 10. pág. 70.
14. Blagg, MA (1913). "Sobre un sustituto sugerido para la ley de Bode". Monthly Notices of the Royal Astronomical Society . 73 : 414–22. Bibcode :1913MNRAS..73..414B. doi : 10.1093/mnras/73.6.414 .
15. Lobban, GG; Roy, AE ; Brown, JC (octubre de 1982). "Una revisión de la fórmula de Blagg a la luz de los anillos y lunas planetarias recientemente descubiertos". Revista de la Asociación Astronómica Británica . 92 (6): 260–263. Código Bibliográfico :1982JBAA...92..260L.
16. Malcolm, Roy (1955). "¿Es la ley de Bode una coincidencia?". Astounding Science Fiction . LV (5).
17. Richardson, DE (1945). "Distancias de los planetas al Sol y de los satélites a sus primarios en los sistemas de satélites de Júpiter, Saturno y Urano". Astronomía popular . Vol. 53. págs. 14–26.
18. Nieto, Michael Martin (1972). La ley de Titius-Bode de las distancias planetarias: su historia y teoría (1.ª ed.). Pergamon Press. doi :10.1016/C2013-0-02478-4. ISBN 978-0-08-016784-8.
19. Carroll, Bradley W.; Ostlie, Dale A. (2007). Introducción a la astrofísica moderna. Pearson Addison-Wesley. págs. 716-717. ISBN 978-0-8053-0402-2.
20. Wayne Hayes; Scott Tremaine (octubre de 1998). "Ajuste de sistemas planetarios aleatorios seleccionados a las leyes de Titius-Bode" (PDF) . Icarus . 135 (2): 549. arXiv : astro-ph/9710116 . Bibcode :1998Icar..135..549H. CiteSeerX 10.1.1.27.8254 . doi :10.1006/icar.1998.5999. S2CID  15015134. 
21. F. Graner ; B. Dubrulle (1994). "Leyes de Titius-Bode en el sistema solar. Parte I: La invariancia de escala lo explica todo". Astronomía y astrofísica . 282 (1): 262–268. Bibcode :1994A&A...282..262G.
22. B. Dubrulle ; F. Graner (1994). "Leyes de Titius-Bode en el sistema solar. Parte II: Construye tu propia ley a partir de modelos de disco". Astronomía y Astrofísica . 282 (1): 269–276. Bibcode :1994A&A...282..269D.
23. Cohen, Howard L. (mayo de 1996). "The Titius-Bode relationship revisited". FirstLight (artículo del boletín mensual). Gainesville, FL: Alachua Astronomy Club. Archivado desde el original el 28 de septiembre de 2007. Consultado el 24 de febrero de 2008 , a través de Florida Stars (floridastars.org).
24. Harwit, Martin (1998). Conceptos astrofísicos. Springer. Págs. 27-29. ISBN. 9780387949437– a través de Google Books.
25. Kotliarov, Ivan (21 de junio de 2008). "La ley de Titius-Bode revisada pero no revivida". arXiv : 0806.3532 [physics.space-ph].
26. Poveda, Arcadio y Lara, Patricia (2008). "El sistema exoplanetario de 55 Cancri y la ley de Titus-Bode" (PDF) . Revista Mexicana de Astronomía y Astrofísica (44): 243–246.
27. Dawson, Rebekah I.; Fabrycky, Daniel C. (2010). "Planetas con velocidad radial desaliasados. Un nuevo período corto para la supertierra 55 Cnc e". Astrophysical Journal . 722 (1): 937–953. arXiv : 1005.4050 . Código Bibliográfico :2010ApJ...722..937D. doi :10.1088/0004-637X/722/1/937. S2CID  118592734.
28. "Sección 8.2: ¿Leyes extrasolares similares a las de Titius-Bode?" (PDF) . Observatorio Europeo Austral (ESO.org) (Nota de prensa). La búsqueda HARPS de planetas extrasolares australes. 23 de agosto de 2010. Consultado el 24 de agosto de 2010 .
29. Lara, Patricia (2012). Sobre la ley estructural de los sistemas exoplanetarios . ICNAAM 2012: Conferencia Internacional de Análisis Numérico y Matemática Aplicada. Actas de la Conferencia AIP. Vol. 1479. págs. 2356–2359. Bibcode :2012AIPC.1479.2356L. doi :10.1063/1.4756667.
30. Bovaird, Timothy; Lineweaver, Charles H. (2013). "Predicciones de exoplanetas basadas en la relación generalizada de Titius-Bode". Monthly Notices of the Royal Astronomical Society . 435 (2): 1126. arXiv : 1304.3341 . Bibcode :2013MNRAS.435.1126B. doi : 10.1093/mnras/stt1357 .
31. Huang, Chelsea X.; Bakos, Gaspár Á. (9 de mayo de 2014). "Prueba de las predicciones de la ley de Titius-Bode para sistemas multiplanetarios de Kepler". Avisos mensuales de la Real Sociedad Astronómica . 442 (1): 674–681. arXiv : 1405.2259 . Código Bib : 2014MNRAS.442..674H. doi : 10.1093/mnras/stu906 .
32. Kipping, David (2018). "Predicción de la órbita de TRAPPIST-1i". Notas de investigación de la Sociedad Astronómica Estadounidense . 2 (3): 136. arXiv : 1807.10835 . Código Bibliográfico :2018RNAAS...2..136K. doi : 10.3847/2515-5172/aad6e8 . S2CID:  119005201.
33. Ballesteros, FJ; Fernández-Soto, A.; Martínez, VJ (2019). "Buceando en exoplanetas: ¿Son los mares de agua los más comunes?". Astrobiología . 19 (5): 642–654. Bibcode :2019AsBio..19..642B. doi :10.1089/ast.2017.1720. hdl : 10261/213115 . PMID  30789285. S2CID  73498809.
34. Lara, Patricia; Cordero-Tercero, Guadalupe; Allen, Christine (2020). "La confiabilidad de la relación Titius-Bode y sus implicaciones para la búsqueda de exoplanetas". Publicaciones de la Sociedad Astronómica de Japón . 72 (2). arXiv : 2003.05121 . doi :10.1093/pasj/psz146.

Lectura adicional

• Matthews, Robert (9 de abril de 1994). "La mano fantasmal que separó los planetas". New Scientist . pág. 13.
• Perdijk, HJR "La ley de Titius-Bode explicada". Plantas y planetas. Archivado desde el original el 15 de julio de 2014. Consultado el 26 de enero de 2024 en kpn.nl.{{cite web}}: CS1 maint: URL no apta ( enlace )— místico y especulativo; ref. diagramas faltantes en el archivo
• Parés i Farràs, Ramon, Dr. (2016). Distancias planetarias y ley de Titius-Bode [Distancias planetarias y la ley de Titius-Bode] (PDF) (ensayo de astronomía popular) (en español) . Consultado el 26 de enero de 2024 a través de wix.com.{{cite report}}: CS1 maint: multiple names: authors list (link)— Combinación de la historia de las mediciones de distancias y el desarrollo de la ley de Titius, astrónomos notables involucrados y exposición mediante gráficos y proporciones simples de las distancias planetarias y satelitales modernas