Resistencia a la rodadura

Fuerza que resiste el movimiento cuando un cuerpo rueda sobre una superficie

Figura 1 Rueda dura rodando sobre una superficie blanda y deformándola, lo que da como resultado que la fuerza de reacción R de la superficie tenga un componente que se opone al movimiento. ( W es una carga vertical sobre el eje, F es una fuerza de remolque aplicada al eje, r es el radio de la rueda y se supone que tanto la fricción con el suelo como la fricción en el eje son insignificantes, por lo que no se muestran. La rueda está rodando hacia la izquierda a velocidad constante). Nótese que R es la fuerza resultante de la presión no uniforme en la superficie de contacto de la rueda con la calzada. Esta presión es mayor hacia la parte delantera de la rueda debido a la histéresis.

La resistencia a la rodadura , a veces llamada fricción de rodadura o arrastre de rodadura , es la fuerza que se opone al movimiento cuando un cuerpo (como una pelota , un neumático o una rueda ) rueda sobre una superficie. Es causada principalmente por efectos no elásticos ; es decir, no toda la energía necesaria para la deformación (o movimiento) de la rueda, la plataforma, etc., se recupera cuando se elimina la presión. Dos formas de esto son las pérdidas por histéresis (ver a continuación) y la deformación permanente (plástica) del objeto o la superficie (por ejemplo, el suelo). Tenga en cuenta que el deslizamiento entre la rueda y la superficie también da como resultado la disipación de energía. Aunque algunos investigadores han incluido este término en la resistencia a la rodadura, algunos sugieren que este término de disipación debe tratarse por separado de la resistencia a la rodadura porque se debe al par aplicado a la rueda y al deslizamiento resultante entre la rueda y el suelo, que se llama pérdida por deslizamiento o resistencia al deslizamiento. ^[1] Además, solo la llamada resistencia al deslizamiento implica fricción , por lo tanto, el nombre "fricción de rodadura" es hasta cierto punto un nombre inapropiado.

De manera análoga a la fricción por deslizamiento , la resistencia a la rodadura se expresa a menudo como un coeficiente multiplicado por la fuerza normal. Este coeficiente de resistencia a la rodadura es generalmente mucho menor que el coeficiente de fricción por deslizamiento. ^[2]

Cualquier vehículo con ruedas que se desplace por inercia irá disminuyendo gradualmente su velocidad debido a la resistencia a la rodadura, incluida la de los cojinetes, pero un vagón de tren con ruedas de acero que se desplace sobre raíles de acero rodará más lejos que un autobús de la misma masa con neumáticos de caucho que se desplace sobre asfalto . Los factores que contribuyen a la resistencia a la rodadura son la (cantidad de) deformación de las ruedas, la deformación de la superficie de la calzada y el movimiento debajo de la superficie. Otros factores contribuyentes incluyen el diámetro de la rueda, ^[3] la carga sobre la rueda, la adherencia a la superficie, el deslizamiento y el microdeslizamiento relativo entre las superficies de contacto. Las pérdidas debidas a la histéresis también dependen en gran medida de las propiedades del material de la rueda o neumático y de la superficie. Por ejemplo, un neumático de caucho tendrá una mayor resistencia a la rodadura en una carretera pavimentada que una rueda de ferrocarril de acero sobre un raíl de acero. Además, la arena en el suelo dará más resistencia a la rodadura que el hormigón . El único factor de resistencia a la rodadura no depende de la velocidad.

Causa primaria

Distribución asimétrica de la presión entre cilindros rodantes debido al comportamiento del material viscoelástico (rodamiento hacia la derecha). ^[4]

La causa principal de la resistencia a la rodadura de los neumáticos es la histéresis : ^[5]

Característica de un material deformable, en la que la energía de deformación es mayor que la energía de recuperación. El compuesto de caucho de un neumático presenta histéresis. A medida que el neumático gira bajo el peso del vehículo, experimenta ciclos repetidos de deformación y recuperación, y disipa la pérdida de energía por histéresis en forma de calor. La histéresis es la principal causa de pérdida de energía asociada con la resistencia a la rodadura y se atribuye a las características viscoelásticas del caucho.

— Academia Nacional de Ciencias ^[6]

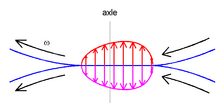
Este principio fundamental se ilustra en la figura de los cilindros rodantes. Si se presionan entre sí dos cilindros iguales, la superficie de contacto es plana. En ausencia de fricción superficial, las tensiones de contacto son normales (es decir, perpendiculares) a la superficie de contacto. Considere una partícula que entra en el área de contacto por el lado derecho, viaja a través de la zona de contacto y sale por el lado izquierdo. Inicialmente, su deformación vertical aumenta, a la que se opone la resistencia del efecto de histéresis. Por lo tanto, se genera una presión adicional para evitar la interpenetración de las dos superficies. Más tarde, su deformación vertical disminuye, a la que se opone nuevamente el efecto de histéresis. En este caso, esto disminuye la presión que se necesita para mantener separados los dos cuerpos.

La distribución de la presión resultante es asimétrica y se desplaza hacia la derecha. La línea de acción de la fuerza vertical (agregada) ya no pasa por los centros de los cilindros. Esto significa que se genera un momento que tiende a retardar el movimiento de balanceo.

Los materiales que tienen un gran efecto de histéresis, como el caucho, que rebotan lentamente, exhiben más resistencia a la rodadura que los materiales con un pequeño efecto de histéresis que rebotan más rápido y de manera más completa, como el acero o la sílice . Los neumáticos de baja resistencia a la rodadura generalmente incorporan sílice en lugar de negro de carbono en sus compuestos de banda de rodadura para reducir la histéresis de baja frecuencia sin comprometer la tracción. ^[7] Tenga en cuenta que los ferrocarriles también tienen histéresis en la estructura de la plataforma de la carretera. ^[8]

Definiciones

En sentido amplio, la "resistencia a la rodadura" específica (para vehículos) es la fuerza por unidad de peso del vehículo necesaria para mover el vehículo sobre terreno llano a una velocidad lenta constante donde la resistencia aerodinámica (resistencia del aire) es insignificante y también donde no hay fuerzas de tracción (motor) ni frenos aplicados. En otras palabras, el vehículo se movería por inercia si no fuera por la fuerza para mantener una velocidad constante. ^[9] Este sentido amplio incluye la resistencia de los cojinetes de las ruedas, la energía disipada por la vibración y la oscilación tanto de la plataforma de la carretera como del vehículo, y el deslizamiento de la rueda sobre la superficie de la plataforma de la carretera (pavimento o raíl).

Pero existe un sentido aún más amplio que incluiría la energía desperdiciada por el deslizamiento de las ruedas debido al par aplicado desde el motor. Esto incluye el aumento de potencia requerida debido al aumento de la velocidad de las ruedas, donde la velocidad tangencial de la(s) rueda(s) motrices se vuelve mayor que la velocidad del vehículo debido al deslizamiento. Dado que la potencia es igual a la fuerza multiplicada por la velocidad y la velocidad de la rueda ha aumentado, la potencia requerida ha aumentado en consecuencia.

La "resistencia a la rodadura" pura de un tren es la que se produce debido a la deformación y al posible deslizamiento menor en el contacto entre la rueda y la carretera. ^[10] En el caso de un neumático de caucho, se produce una pérdida de energía análoga en todo el neumático, pero se sigue llamando "resistencia a la rodadura". En sentido amplio, la "resistencia a la rodadura" incluye la resistencia de los cojinetes de las ruedas, la pérdida de energía por la vibración tanto de la plataforma de la carretera (y de la tierra que se encuentra debajo) como del propio vehículo, y por el deslizamiento de la rueda, el contacto entre la carretera y los raíles. Los libros de texto sobre ferrocarriles parecen cubrir todas estas fuerzas de resistencia, pero no denominan a su suma "resistencia a la rodadura" (sentido amplio) como se hace en este artículo. Simplemente suman todas las fuerzas de resistencia (incluida la resistencia aerodinámica) y denominan a la suma resistencia básica del tren (o algo similar). ^[11]

Dado que la resistencia a la rodadura del ferrocarril en sentido amplio puede ser varias veces mayor que la resistencia a la rodadura pura ^[12], los valores informados pueden estar en serio conflicto, ya que pueden basarse en diferentes definiciones de "resistencia a la rodadura". Los motores del tren deben, por supuesto, proporcionar la energía necesaria para superar esta resistencia a la rodadura en sentido amplio.

En el caso de los neumáticos, la resistencia a la rodadura se define como la energía que consume un neumático por unidad de distancia recorrida. También se denomina fricción de rodadura o resistencia al rodamiento. Es una de las fuerzas que actúan para oponerse al movimiento del conductor. La razón principal es que cuando los neumáticos están en movimiento y tocan la superficie, esta cambia de forma y provoca la deformación del neumático. ^[13]

En el caso de los vehículos de carretera, se disipa cierta energía al sacudir la calzada (y la tierra que se encuentra debajo de ella), al sacudir el propio vehículo y al deslizar los neumáticos. Pero, aparte de la potencia adicional requerida debido al par motor y a la fricción de los cojinetes de las ruedas, no parece que se haya investigado la resistencia a la rodadura no pura, posiblemente porque la resistencia a la rodadura "pura" de un neumático de caucho es varias veces superior a las resistencias ignoradas. ^[14]

Coeficiente de resistencia a la rodadura

El "coeficiente de resistencia a la rodadura" se define mediante la siguiente ecuación: ^[6] donde $${\displaystyle \ F=C_{rr}N}$$

• ${\displaystyle F}$es la fuerza de resistencia a la rodadura (mostrada como en la figura 1), ${\displaystyle R}$
• ${\displaystyle C_{rr}}$es el coeficiente de resistencia a la rodadura adimensional o coeficiente de fricción de rodadura ( CRF ), y
• ${\displaystyle N}$es la fuerza normal , la fuerza perpendicular a la superficie sobre la que rueda la rueda.

${\displaystyle C_{rr}}$es la fuerza necesaria para empujar (o remolcar) un vehículo con ruedas hacia adelante (a velocidad constante sobre una superficie nivelada, o pendiente cero, con resistencia del aire cero) por unidad de fuerza de peso. Se supone que todas las ruedas son iguales y soportan un peso idéntico. Por lo tanto: significa que solo se necesitarían 0,01 libras para remolcar un vehículo que pesa una libra. Para un vehículo de 1000 libras, se necesitaría 1000 veces más fuerza de remolque, es decir, 10 libras. Se podría decir que está en lb(fuerza de remolque)/lb(peso del vehículo). Dado que esta lb/lb es fuerza dividida por fuerza, es adimensional. Multiplíquelo por 100 y obtendrá el porcentaje (%) del peso del vehículo necesario para mantener una velocidad lenta y constante. se multiplica a menudo por 1000 para obtener las partes por mil, que es lo mismo que kilogramos (kg fuerza) por tonelada métrica (tonelada = 1000 kg), ^[15] que es lo mismo que libras de resistencia por 1000 libras de carga o Newtons/kilo-Newton, etc. Para los ferrocarriles estadounidenses, tradicionalmente se ha utilizado lb/tonelada; esto es simplemente . Por lo tanto, todas son simplemente medidas de resistencia por unidad de peso del vehículo. Si bien todas son "resistencias específicas", a veces se las llama simplemente "resistencia" aunque en realidad son un coeficiente (ratio) o un múltiplo del mismo. Si se utilizan libras o kilogramos como unidades de fuerza, la masa es igual al peso (en la gravedad de la Tierra, un kilogramo de masa pesa un kilogramo y ejerce un kilogramo de fuerza), por lo que se podría afirmar que también es la fuerza por unidad de masa en dichas unidades. El sistema SI utilizaría N/tonelada (N/T, N/t), que es y es fuerza por unidad de masa, donde g es la aceleración de la gravedad en unidades SI (metros por segundo al cuadrado). ^[16] ${\displaystyle \ C_{rr}=0.01}$ ${\displaystyle C_{rr}}$ ${\displaystyle C_{rr}}$ ${\displaystyle C_{rr}}$ ${\displaystyle 2000C_{rr}}$ ${\displaystyle C_{rr}}$ ${\displaystyle 1000gC_{rr}}$

Lo anterior muestra que la resistencia es proporcional a la velocidad, las cargas, el par motor, la rugosidad de la superficie, el diámetro, el inflado/desgaste de los neumáticos, etc., pero no muestra explícitamente ninguna variación con ellos, ya que varía en función de esos factores. De la definición anterior podría parecer que la resistencia a la rodadura es directamente proporcional al peso del vehículo, pero no es así. ${\displaystyle C_{rr}}$ ${\displaystyle C_{rr}}$ ${\displaystyle C_{rr}}$

Medición

Existen al menos dos modelos populares para calcular la resistencia a la rodadura.

1. "Coeficiente de resistencia a la rodadura (RRC). El valor de la fuerza de resistencia a la rodadura dividido por la carga de la rueda. La Sociedad de Ingenieros Automotrices (SAE) ha desarrollado prácticas de prueba para medir el RRC de los neumáticos. Estas pruebas ( SAE J1269 y SAE J2452 ) se realizan generalmente ^{[ cita requerida ]} en neumáticos nuevos. Cuando se miden utilizando estas prácticas de prueba estándar, la mayoría de los neumáticos nuevos para pasajeros han informado RRC que van desde 0,007 a 0,014". ^[6] En el caso de los neumáticos de bicicleta, se alcanzan valores de 0,0025 a 0,005. ^[17] Estos coeficientes se miden en rodillos, con medidores de potencia en superficies de carretera o con pruebas de desaceleración. En los dos últimos casos, se debe restar el efecto de la resistencia del aire o realizar las pruebas a velocidades muy bajas.
2. El coeficiente de resistencia a la rodadura b , que tiene la dimensión de longitud , es aproximadamente (debido a la aproximación de ángulo pequeño de ) igual al valor de la fuerza de resistencia a la rodadura multiplicado por el radio de la rueda dividido por la carga de la rueda. ^[3] ${\displaystyle \cos(\theta )=1}$
3. La norma ISO 18164:2005 se utiliza para probar la resistencia a la rodadura en Europa.

Los resultados de estas pruebas pueden ser difíciles de obtener para el público en general, ya que los fabricantes prefieren publicitar la "comodidad" y el "rendimiento".

Fórmulas físicas

El coeficiente de resistencia a la rodadura de una rueda rígida lenta sobre una superficie perfectamente elástica, no ajustada a la velocidad, se puede calcular mediante ^{[18] [ cita requerida ]} donde $${\displaystyle C_{rr}={\sqrt {z/d}}}$$

• ${\displaystyle z}$es la profundidad del hundimiento
• ${\displaystyle d}$es el diámetro de la rueda rígida

La fórmula empírica para ruedas de vagones mineros de hierro fundido sobre rieles de acero es: ^[19] donde ${\displaystyle C_{rr}}$ $${\displaystyle C_{rr}=0.0048(18/D)^{\frac {1}{2}}(100/W)^{\frac {1}{4}}={\frac {0.0643988}{\sqrt[{4}]{WD^{2}}}}}$$

• ${\displaystyle D}$es el diámetro de la rueda en pulgadas
• ${\displaystyle W}$¿Es la carga sobre la rueda en libras-fuerza?

Como alternativa al uso de C r r {\displaystyle C_{rr}} se puede utilizar , que es un coeficiente de resistencia a la rodadura o coeficiente de fricción de rodadura diferente con dimensión de longitud. Se define mediante la siguiente fórmula: ^[3] donde ${\displaystyle b}$ $${\displaystyle F={\frac {Nb}{r}}}$$

• ${\displaystyle F}$es la fuerza de resistencia a la rodadura (mostrada en la figura 1),
• ${\displaystyle r}$es el radio de la rueda,
• ${\displaystyle b}$es el coeficiente de resistencia a la rodadura o coeficiente de fricción de rodadura con dimensión de longitud, y
• ${\displaystyle N}$es la fuerza normal (igual a W , no R , como se muestra en la figura 1).

La ecuación anterior, donde la resistencia es inversamente proporcional al radio, parece estar basada en la desacreditada "ley de Coulomb" (ni la ley del cuadrado inverso de Coulomb ni la ley de fricción de Coulomb) ^{[ cita requerida ]} . Véase dependencia del diámetro. Igualando esta ecuación con la fuerza por el coeficiente de resistencia a la rodadura y despejando para , se obtiene = . Por lo tanto, si una fuente da el coeficiente de resistencia a la rodadura ( ) como un coeficiente adimensional, se puede convertir a , que tiene unidades de longitud, multiplicando por el radio de la rueda . ${\displaystyle r}$ ${\displaystyle b}$ ${\displaystyle b}$ ${\displaystyle C_{rr}r}$ ${\displaystyle C_{rr}}$ ${\displaystyle b}$ ${\displaystyle C_{rr}}$ ${\displaystyle r}$

Ejemplos de coeficientes de resistencia a la rodadura

Tabla de ejemplos de coeficientes de resistencia a la rodadura: [3]

Por ejemplo, en la gravedad terrestre, un automóvil de 1000 kg sobre asfalto necesitará una fuerza de alrededor de 100  newtons para rodar (1000 kg × 9,81 m/s ² × 0,01 = 98,1 N).

Dependencia del diámetro

Diligencias y ferrocarriles

Según Dupuit (1837), la resistencia a la rodadura (de carruajes con ruedas de madera y neumáticos de hierro) es aproximadamente inversamente proporcional a la raíz cuadrada del diámetro de la rueda. ^[34] Esta regla se ha verificado experimentalmente para ruedas de hierro fundido (de 8″ a 24″ de diámetro) sobre raíles de acero ^[35] y para ruedas de carruajes del siglo XIX. ^[33] Pero hay otras pruebas sobre ruedas de carruajes que no concuerdan. ^[33] La teoría de un cilindro rodando sobre una calzada elástica también da esta misma regla ^[36] Estas contradicen pruebas anteriores (1785) de Coulomb sobre cilindros de madera rodantes, donde Coulomb informó que la resistencia a la rodadura era inversamente proporcional al diámetro de la rueda (conocida como "ley de Coulomb"). ^[37] Sin embargo, esta "ley de Coulomb" controvertida (o mal aplicada) todavía se encuentra en los manuales.

Neumáticos

En el caso de neumáticos sobre pavimento duro, se informa que el efecto del diámetro sobre la resistencia a la rodadura es insignificante (dentro de un rango práctico de diámetros). ^{[38] [39]}

Dependencia del par aplicado

El par motor necesario para superar la resistencia a la rodadura y mantener una velocidad constante en terreno llano (sin resistencia del aire) se puede calcular mediante: donde ${\displaystyle T}$ ${\displaystyle R_{r}}$ $${\displaystyle T={\frac {V_{s}}{\Omega }}R_{r}}$$

• ${\displaystyle V_{s}}$es la velocidad lineal del cuerpo (en el eje), y
• ${\displaystyle \Omega }$su velocidad de rotación.

Cabe destacar que normalmente no es igual al radio del cuerpo rodante como resultado del deslizamiento de la rueda. ^{[40] [41] [42]} El deslizamiento entre la rueda y el suelo ocurre inevitablemente siempre que se aplica un par de accionamiento o de frenado a la rueda. ^{[43] [44]} En consecuencia, la velocidad lineal del vehículo difiere de la velocidad circunferencial de la rueda. Es de destacar que el deslizamiento no ocurre en las ruedas motrices, que no están sujetas al par de accionamiento, en diferentes condiciones excepto el frenado. Por lo tanto, la resistencia a la rodadura, es decir, la pérdida por histéresis, es la principal fuente de disipación de energía en las ruedas o ejes motrices, mientras que en las ruedas y ejes motrices la resistencia al deslizamiento, es decir, la pérdida debido al deslizamiento de la rueda, juega el papel al igual que la resistencia a la rodadura. ^[45] La importancia de la resistencia a la rodadura o al deslizamiento depende en gran medida de la fuerza de tracción , el coeficiente de fricción, la carga normal, etc. ^[46] ${\displaystyle V_{s}/\Omega }$

Todas las ruedas

El "par aplicado" puede ser un par motor aplicado por un motor (a menudo a través de una transmisión ) o un par de frenado aplicado por los frenos (incluido el frenado regenerativo ). Dichos pares dan como resultado una disipación de energía (por encima de la debida a la resistencia básica a la rodadura de un vehículo que rueda libremente, es decir, excepto la resistencia al deslizamiento). Esta pérdida adicional se debe en parte al hecho de que hay cierto deslizamiento de la rueda y, en el caso de los neumáticos, hay una mayor flexión de las paredes laterales debido al par. El deslizamiento se define de modo que un deslizamiento del 2 % significa que la velocidad circunferencial de la rueda motriz supera la velocidad del vehículo en un 2 %.

Un pequeño porcentaje de deslizamiento puede dar como resultado una resistencia al deslizamiento mucho mayor que la resistencia básica a la rodadura. Por ejemplo, en el caso de los neumáticos, un deslizamiento del 5 % puede traducirse en un aumento del 200 % de la resistencia a la rodadura. ^[47] Esto se debe en parte a que la fuerza de tracción aplicada durante este deslizamiento es muchas veces mayor que la fuerza de resistencia a la rodadura y, por lo tanto, se aplica mucha más potencia por unidad de velocidad (recuerde que potencia = fuerza x velocidad, de modo que la potencia por unidad de velocidad es simplemente fuerza). Por lo tanto, un pequeño aumento porcentual de la velocidad circunferencial debido al deslizamiento puede traducirse en una pérdida de potencia de tracción que puede incluso superar la pérdida de potencia debida a la resistencia básica (ordinaria) a la rodadura. En el caso de los ferrocarriles, este efecto puede ser incluso más pronunciado debido a la baja resistencia a la rodadura de las ruedas de acero.

Se ha demostrado que, en el caso de un automóvil de pasajeros, cuando la fuerza de tracción es aproximadamente el 40 % de la tracción máxima, la resistencia al deslizamiento es casi igual a la resistencia básica a la rodadura (pérdida por histéresis). Pero, en el caso de una fuerza de tracción igual al 70 % de la tracción máxima, la resistencia al deslizamiento se vuelve diez veces mayor que la resistencia básica a la rodadura. ^[1]

Ruedas de acero para ferrocarril

Para aplicar cualquier tracción a las ruedas, se requiere cierto deslizamiento de las ruedas. ^[48] Para los trenes que suben una pendiente, este deslizamiento normalmente es del 1,5% al ​​2,5%.

El deslizamiento (también conocido como deslizamiento ) normalmente es aproximadamente directamente proporcional al esfuerzo de tracción . Una excepción es si el esfuerzo de tracción es tan alto que la rueda está cerca de deslizarse sustancialmente (más de un pequeño porcentaje como se discutió anteriormente), entonces el deslizamiento aumenta rápidamente con el esfuerzo de tracción y ya no es lineal. Con un esfuerzo de tracción ligeramente mayor aplicado, la rueda gira sin control y la adherencia disminuye, lo que hace que la rueda gire aún más rápido. Este es el tipo de deslizamiento que se observa a simple vista: el deslizamiento de, digamos, el 2% para la tracción solo se observa con instrumentos. Un deslizamiento tan rápido puede resultar en un desgaste o daño excesivos.

Neumáticos

La resistencia a la rodadura aumenta considerablemente con el par aplicado. Con pares elevados, que aplican una fuerza tangencial a la carretera de aproximadamente la mitad del peso del vehículo, la resistencia a la rodadura puede triplicarse (un aumento del 200 %). ^[47] Esto se debe en parte a un deslizamiento de aproximadamente el 5 %. El aumento de la resistencia a la rodadura con el par aplicado no es lineal, sino que aumenta a un ritmo más rápido a medida que el par aumenta.

Dependencia de la carga de la rueda

Ruedas de acero para ferrocarril

El coeficiente de resistencia a la rodadura, Crr, disminuye significativamente a medida que aumenta el peso del vagón por rueda. ^[49] Por ejemplo, un vagón de carga vacío tenía aproximadamente el doble de Crr que un vagón cargado (Crr=0,002 frente a Crr=0,001). Esta misma "economía de escala" se muestra en las pruebas de vagones de ferrocarril de minas. ^[50] El Crr teórico para una rueda rígida que rueda sobre una plataforma elástica muestra que Crr es inversamente proporcional a la raíz cuadrada de la carga. ^[36]

Si Crr depende de la carga de la rueda según una regla de raíz cuadrada inversa, entonces para un aumento de la carga del 2% solo se produce un aumento del 1% en la resistencia a la rodadura. ^[51]

Neumáticos

En el caso de los neumáticos, la dirección del cambio de Crr (coeficiente de resistencia a la rodadura) depende de si el inflado del neumático aumenta o no con el aumento de la carga. ^[52] Se informa que, si la presión de inflado aumenta con la carga según un "programa" (indefinido), entonces un aumento del 20% en la carga disminuye Crr en un 3%. Pero, si la presión de inflado no cambia, entonces un aumento del 20% en la carga da como resultado un aumento del 4% en Crr. Por supuesto, esto aumentará la resistencia a la rodadura en un 20% debido al aumento de la carga más 1,2 x 4% debido al aumento de Crr, lo que resulta en un aumento del 24,8% en la resistencia a la rodadura. ^[53]

Dependencia de la curvatura de la calzada

General

Cuando un vehículo ( vehículo de motor o tren ) toma una curva, la resistencia a la rodadura suele aumentar. Si la curva no está peraltada de forma que se contrarreste exactamente la fuerza centrífuga con una fuerza centrípeta igual y opuesta debido al peralte, entonces habrá una fuerza lateral desequilibrada neta sobre el vehículo. Esto dará como resultado un aumento de la resistencia a la rodadura. El peralte también se conoce como "peralte" o "inclinación" (que no debe confundirse con la inclinación de un raíl ). En el caso de los ferrocarriles, esto se denomina resistencia a la curva , pero en el caso de las carreteras se ha denominado (al menos una vez) resistencia a la rodadura debido a las curvas .

Sonido

La fricción de rodadura genera energía sonora (vibratoria), ya que la energía mecánica se convierte en esta forma de energía debido a la fricción. Uno de los ejemplos más comunes de fricción de rodadura es el movimiento de los neumáticos de los vehículos de motor en una carretera , un proceso que genera sonido como subproducto. ^[54] El sonido generado por los neumáticos de automóviles y camiones cuando ruedan (especialmente perceptible a velocidades de autopista) se debe principalmente a la percusión de las bandas de rodadura de los neumáticos y a la compresión (y posterior descompresión) del aire capturado temporalmente dentro de las bandas de rodadura. ^[55]

Factores que influyen en los neumáticos

Varios factores afectan la magnitud de la resistencia al rodamiento que genera un neumático:

• Como se mencionó en la introducción: radio de la rueda, velocidad de avance, adherencia a la superficie y microdeslizamiento relativo.
• Material: el uso de diferentes rellenos y polímeros en la composición de los neumáticos puede mejorar la tracción y reducir la histéresis. Una forma habitual de reducir la resistencia a la rodadura es sustituir parte del negro de carbono por sílice-silano, un material más caro. ^[6] Se ha demostrado que el uso de materiales exóticos, como la nanoarcilla, reduce la resistencia a la rodadura en neumáticos de caucho de alto rendimiento. ^[56] También se pueden utilizar disolventes para hinchar los neumáticos macizos, lo que reduce la resistencia a la rodadura. ^[57]
• Dimensiones: la resistencia al rodamiento en los neumáticos está relacionada con la flexión de las paredes laterales y el área de contacto del neumático ^[58] Por ejemplo, a la misma presión, los neumáticos de bicicleta más anchos se flexionan menos en las paredes laterales a medida que ruedan y, por lo tanto, tienen una menor resistencia al rodamiento (aunque una mayor resistencia del aire). ^[58]
• Grado de inflado: una presión más baja en los neumáticos produce una mayor flexión de las paredes laterales y una mayor resistencia a la rodadura. ^[58] Esta conversión de energía en las paredes laterales aumenta la resistencia y también puede provocar sobrecalentamiento y puede haber jugado un papel en los infames accidentes de vuelco del Ford Explorer .
• El inflado excesivo de los neumáticos (como los de una bicicleta) puede no reducir la resistencia general a la rodadura, ya que el neumático puede saltar y rebotar sobre la superficie de la carretera. Se sacrifica la tracción y la fricción general de rodadura puede no reducirse a medida que cambia la velocidad de rotación de la rueda y aumenta el deslizamiento. ^{[ cita requerida ]}
• La deflexión de la pared lateral no es una medida directa de la fricción de rodadura. Un neumático de alta calidad con una carcasa de alta calidad (y flexible) permitirá una mayor flexión por pérdida de energía que un neumático barato con una pared lateral rígida. ^{[ cita requerida ]} Nuevamente, en una bicicleta, un neumático de calidad con una carcasa flexible seguirá rodando más fácilmente que un neumático barato con una carcasa rígida. De manera similar, como se indica en los neumáticos para camiones de Goodyear, un neumático con una carcasa que "ahorra combustible" beneficiará el ahorro de combustible a lo largo de muchas vidas útiles de la banda de rodadura (es decir, recauchutado), mientras que un neumático con un diseño de banda de rodadura que "ahorra combustible" solo se beneficiará hasta que la banda de rodadura se desgaste.
• En los neumáticos, el grosor y la forma de la banda de rodadura tienen mucho que ver con la resistencia a la rodadura. Cuanto más gruesa y contorneada sea la banda de rodadura, mayor será la resistencia a la rodadura ^[58]. Por lo tanto, los neumáticos de bicicleta "más rápidos" tienen muy poca banda de rodadura y los camiones pesados ​​obtienen el mejor ahorro de combustible a medida que la banda de rodadura del neumático se desgasta.
• Los efectos del diámetro parecen ser insignificantes, siempre que el pavimento sea duro y el rango de diámetros sea limitado. Véase la dependencia del diámetro.
• Prácticamente todos los récords mundiales de velocidad se han conseguido con ruedas relativamente estrechas, ^{[ cita requerida ]} probablemente debido a su ventaja aerodinámica a alta velocidad, que es mucho menos importante a velocidades normales.
• Temperatura: tanto en neumáticos sólidos como neumáticos, se ha descubierto que la resistencia a la rodadura disminuye a medida que aumenta la temperatura (dentro de un rango de temperaturas: es decir, hay un límite superior para este efecto) ^{[59] [60]} Para un aumento de temperatura de 30 °C a 70 °C, la resistencia a la rodadura disminuyó en un 20-25%. ^[61] Los corredores calientan sus neumáticos antes de la carrera, pero esto se utiliza principalmente para aumentar la fricción de los neumáticos en lugar de disminuir la resistencia a la rodadura.

Ferrocarriles: componentes de la resistencia a la rodadura

En un sentido amplio, la resistencia a la rodadura se puede definir como la suma de componentes ^[62] ):

1. Pérdidas de par en los cojinetes de las ruedas.
2. Resistencia a la rodadura pura.
3. Deslizamiento de la rueda sobre el carril.
4. Pérdida de energía en la plataforma de la carretera (y en la tierra).
5. Pérdida de energía por oscilación del material rodante ferroviario.

Las pérdidas de par en los cojinetes de las ruedas se pueden medir como una resistencia a la rodadura en la llanta de la rueda, Crr. Los ferrocarriles normalmente utilizan cojinetes de rodillos que son cilíndricos (Rusia) ^[63] o cónicos (Estados Unidos). ^[64] La resistencia a la rodadura específica en los cojinetes varía tanto con la carga de la rueda como con la velocidad. ^[65] La resistencia a la rodadura de los cojinetes de las ruedas es más baja con cargas elevadas en los ejes y velocidades intermedias de 60 a 80 km/h con un Crr de 0,00013 (carga por eje de 21 toneladas). Para vagones de mercancías vacíos con cargas por eje de 5,5 toneladas, Crr sube a 0,00020 a 60 km/h, pero a una velocidad baja de 20 km/h aumenta a 0,00024 y a una velocidad alta (para trenes de mercancías) de 120 km/h es 0,00028. El Crr obtenido anteriormente se suma al Crr de los otros componentes para obtener el Crr total para las ruedas.

Comparación de la resistencia a la rodadura de vehículos de carretera y trenes

La resistencia a la rodadura de las ruedas de acero sobre los raíles de acero de un tren es mucho menor que la de las ruedas de caucho de un automóvil o un camión. El peso de los trenes varía mucho; en algunos casos pueden ser mucho más pesados ​​por pasajero o por tonelada neta de carga que un automóvil o un camión, pero en otros casos pueden ser mucho más ligeros.

Como ejemplo de un tren de pasajeros muy pesado, en 1975, los trenes de pasajeros de Amtrak pesaban un poco más de 7 toneladas por pasajero, ^[66] lo que es mucho más pesado que el promedio de un poco más de una tonelada por pasajero para un automóvil. Esto significa que, en el caso de un tren de pasajeros de Amtrak en 1975, gran parte del ahorro de energía que se obtuvo gracias a la menor resistencia a la rodadura se perdió debido a su mayor peso.

Un ejemplo de tren de pasajeros de alta velocidad muy ligero es el Shinkansen de la serie N700 , que pesa 715 toneladas y transporta 1323 pasajeros, lo que da como resultado un peso por pasajero de aproximadamente media tonelada. Este menor peso por pasajero, combinado con la menor resistencia a la rodadura de las ruedas de acero sobre raíles de acero, significa que un Shinkansen N700 es mucho más eficiente energéticamente que un automóvil típico.

En el caso del transporte de mercancías, CSX realizó una campaña publicitaria en 2013 afirmando que sus trenes de mercancías mueven "una tonelada de mercancías a 436 millas con un galón de combustible", mientras que algunas fuentes afirman que los camiones mueven una tonelada de mercancías a unas 130 millas por galón de combustible, lo que indica que los trenes son más eficientes en general.

Véase también

• Coeficiente de fricción
• Neumáticos de baja resistencia a la rodadura
• Maglev ( Levitación magnética , eliminación del rodamiento y, por tanto, de la resistencia al rodamiento)
• Cojinete de elementos rodantes

Referencias

1. Sina, Naser; Esfahanian, Vahid; Yazdi, Mohammad Reza Hairi; Azadi, Shahram (18 de abril de 2018). "SAE MOBILUS". SAE International Journal of Passenger Cars - Mechanical Systems . 11 (2): 167–176. doi :10.4271/06-11-02-0014 . Consultado el 19 de abril de 2021 .
2. Peck, William Guy (1859). Elementos de mecánica: para uso de universidades, academias y escuelas secundarias. AS Barnes & Burr: Nueva York. pág. 135. Consultado el 9 de octubre de 2007. La fricción de rodadura es menor que la fricción de deslizamiento.
3. Hibbeler, RC (2007). Ingeniería mecánica: estática y dinámica (undécima edición). Pearson, Prentice Hall. pp. 441–442. ISBN 9780132038096.
4. "Guía de usuario de CONTACT, Contacto rodante y deslizante con fricción. Informe técnico TR09-03 versión v16.1. VORtech, 2016" (PDF) . Consultado el 11 de julio de 2017 .
5. Manual sobre la resistencia a la rodadura de neumáticos Clark, Samuel Kelly; Dodge, Richard N. 1979
6. "Neumáticos y economía de combustible de vehículos de pasajeros: informar a los consumidores, mejorar el rendimiento - Informe especial 286. Academia Nacional de Ciencias, Junta de Investigación del Transporte, 2006" (PDF) . Consultado el 11 de agosto de 2007 .
7. Tyres-Online: Los beneficios del sílice en el diseño de neumáticos Archivado el 4 de febrero de 2013 en Wayback Machine
8. Astakhov, pág. 85
9. Un ejemplo de tal uso para los ferrocarriles se encuentra aquí.
10. Deev, pág. 79. Hay, pág. 68
11. Астахов, Capítulo. IV, pág. 73+; Деев, secta. 5,2 p. 78+; Hay, cap. 6 "Resistencia del tren" pág. 67+
12. Астахов, Fig. 4.14, pág. 107
13. "Resistencia a la rodadura y ahorro de combustible" (PDF) . Archivado desde el original (PDF) el 8 de abril de 2016.
14. Si se asumiera que los coeficientes de resistencia (Crr) para los vehículos de motor fueran los mismos que para los trenes, entonces para los trenes las resistencias ignoradas tomadas en conjunto tienen un Crr de aproximadamente 0,0004 (ver Астахов, Fig. 4.14, p.107 a 20 km/h y suponga un Crr total = 0,0010 basado en la Fig. 3.8, p.50 (cojinetes lisos) y ajuste para cojinetes de rodillos basado en un delta Crr de 0,00035 como se lee en las Figs. 4.2 y 4.4 en las pp. 74, 76). Compare este Crr de 0,0004 con los Crr de los neumáticos de los vehículos de motor de al menos 10 veces más altos según "Ejemplos de coeficientes de resistencia a la rodadura" en este artículo
15. Астахов utiliza kgf/tonelada en todo su libro.
16. Deev utiliza la notación N/T. Véanse las páginas 78-84.
17. Willett, Kraig. "Roller Data" (Datos de rodillos). www.biketechreview.com . Consultado el 5 de agosto de 2017 .
18. Guiggiani, Massimo (5 de mayo de 2018). La ciencia de la dinámica de vehículos . Springer Cham. pág. 22. ISBN 978-3-319-73220-6.
19. Hersey, ecuación (2), pág. 83
20. Astakhov, pág. 81.
21. "Coeficientes de fricción en cojinetes". Coeficientes de fricción . Consultado el 7 de febrero de 2012 .
22. ETH - PAC-Car II vs PAC-Car I - Técnicas
23. Roche, Schinkel, Storey, Humphris y Guelden, "La velocidad de la luz". ISBN 0-7334-1527-X 
24. Hay, Fig. 6-2 p.72 (no se utiliza el peor caso mostrado de 0,0036 porque es probable que sea erróneo)
25. Астахов, Figs. 3.8, 3.9, 3.11, págs. 50-55; Figs. 2.3, 2.4 págs. 35-36. (El peor caso es 0,0024 para una carga por eje de 5,95 toneladas con cojinetes lisos (de fricción, no de rodillos) obsoletos)
26. Астахов, Fig. 2.1, p.22
27. Hersey, Tabla 6, pág. 267
28. "Datos del rodillo" (PDF) .
29. Crr para neumáticos de camiones grandes según Michelin
30. Anexo 1, Parte A. Neumáticos de la categoría C1 (turismos) del Reglamento (UE) 2020/740 del Parlamento Europeo y del Consejo, de 25 de mayo de 2020, sobre el etiquetado de los neumáticos en relación con la eficiencia de combustible y otros parámetros
31. Informe Sello Verde 2003
32. Gillespie ISBN 1-56091-199-9 p117 
33. Baker, Ira O., "Tratado sobre caminos y pavimentos". Nueva York, John Wiley, 1914. Stagecoach: Tabla 7, pág. 28. Diámetro: págs. 22-23. Este libro informa sobre unos cientos de valores de resistencia a la rodadura para varios vehículos de tracción animal en diversas condiciones, principalmente a partir de datos del siglo XIX.
34. Hersey, apartado: "El fin de la edad oscura", p. 261
35. Hersey, subsección: "Fricción de rodadura estática", p.266.
36. Williams, 1994, Cap. "Contactos rodantes", ecuación 11.1, pág. 409.
37. Hersey, apartado: "Coulomb sobre cilindros de madera", pág. 260
38. Oficina Nacional de Normas de EE. UU., Fig. 1.13
39. Algunos ^{[¿ quiénes? ]} piensan que las ruedas de neumáticos más pequeños, en igualdad de condiciones, tienden a tener una mayor resistencia a la rodadura que las ruedas más grandes. Sin embargo, en algunas pruebas de laboratorio, como los resultados de la prueba Greenspeed (fecha de acceso = 2007-10-27), las ruedas más pequeñas parecieron tener pérdidas similares o menores que las ruedas grandes, pero estas pruebas se realizaron haciendo rodar las ruedas contra un tambor de diámetro pequeño, lo que teóricamente eliminaría la ventaja de las ruedas de diámetro grande, haciendo que las pruebas sean irrelevantes para resolver este problema. Otro contraejemplo de la afirmación de que las ruedas más pequeñas tienen una mayor resistencia a la rodadura se puede encontrar en el área de las carreras de velocidad máxima en cajas de jabón. En esta carrera, las velocidades han aumentado a medida que los diámetros de las ruedas han disminuido hasta en un 50%. Esto podría sugerir que la resistencia a la rodadura puede no estar aumentando significativamente con un diámetro menor dentro de un rango práctico, si se ha controlado alguna de las muchas variables involucradas. Ver la página de discusión .
40. Zéhil, Gérard-Philippe; Gavin, Henri P. (2013). "Formulación tridimensional de elementos de contorno de una capa viscoelástica incompresible de espesor finito aplicada a la resistencia a la rodadura de una esfera rígida". Revista internacional de sólidos y estructuras . 50 (6): 833–842. doi : 10.1016/j.ijsolstr.2012.11.020 .
41. Zéhil, Gérard-Philippe; Gavin, Henri P. (2013). "Algoritmos simples para resolver problemas de contacto rodante por fricción en estado estacionario en dos y tres dimensiones". Revista internacional de sólidos y estructuras . 50 (6): 843–852. doi : 10.1016/j.ijsolstr.2012.11.021 .
42. Zéhil, Gérard-Philippe; Gavin, Henri P. (2013). "Enfoques simplificados para la resistencia al rodamiento viscoelástico". Revista internacional de sólidos y estructuras . 50 (6): 853–862. doi : 10.1016/j.ijsolstr.2012.09.025 .
43. Sina, Naser; Esfahanian, Vahid; Yazdi, Mohammad Reza Hairi; Azadi, Shahram (18 de abril de 2018). "SAE MOBILUS". SAE International Journal of Passenger Cars - Mechanical Systems . 11 (2): 167–176. doi :10.4271/06-11-02-0014 . Consultado el 19 de abril de 2021 .
44. Sina, Naser; Hairi Yazdi, Mohammad Reza; Esfahanian, Vahid (1 de marzo de 2020). "Un nuevo método para mejorar la eficiencia energética del vehículo: minimización de la pérdida de potencia de los neumáticos". Actas de la Institución de Ingenieros Mecánicos, Parte D: Revista de Ingeniería Automotriz . 234 (4): 1153–1166. doi :10.1177/0954407019861241. ISSN  0954-4070. S2CID  199099736.
45. Sina, Naser; Nasiri, Sayyad; Karkhaneh, Vahid (1 de noviembre de 2015). "Efectos de las cargas resistivas y la presión de inflado de los neumáticos en las pérdidas de potencia de los neumáticos y las emisiones de CO2 en condiciones del mundo real". Applied Energy . 157 : 974–983. doi :10.1016/j.apenergy.2015.04.010. ISSN  0306-2619.
46. Sina, Naser; Esfahanian, Vahid; Yazdi, Mohammad Reza Hairi; Azadi, Shahram (18 de abril de 2018). "SAE MOBILUS". SAE International Journal of Passenger Cars - Mechanical Systems . 11 (2): 167–176. doi :10.4271/06-11-02-0014 . Consultado el 19 de abril de 2021 .
47. Roberts, Fig. 17: "Efecto de la transmisión del par en la resistencia a la rodadura", pág. 71
48. Деев, p.30 incluyendo la ecuación (2.7) y la figura 2.3
49. Астахов, Figs. 3.8, 3.9, 3.11, págs. 50-55. Hay, Fig. 60-2, pág. 72 muestra los mismos fenómenos pero tiene valores más altos para Crr y no se informa aquí desde que los ferrocarriles en 2011 [1]. afirmaban aproximadamente el mismo valor que Астахов
50. Hersey, Tabla 6, pág. 267
51. Según esta suposición, donde es la fuerza de resistencia a la rodadura y es la fuerza de carga normal sobre la rueda debido al peso del vehículo, y es una constante. Se puede demostrar fácilmente mediante la diferenciación de con respecto a utilizando esta regla que ${\displaystyle F=kN^{0.5}}$ ${\displaystyle F}$ ${\displaystyle N}$ ${\displaystyle k}$ ${\displaystyle F}$ ${\displaystyle N}$ ${\displaystyle {\operatorname {d} N \over N}=2{\operatorname {d} F \over F}}$
52. Roberts, págs. 60-61.
53. [2] Relación entre la presión de los neumáticos y la fuerza de resistencia a la rodadura a distintas velocidades del vehículo | Apiwat Suyabodha | Departamento de Ingeniería Automotriz, Universidad de Rangsit, Lak-hok, Pathumthani, Tailandia | 2017
54. Hogan, C. Michael (1973). "Análisis del ruido en las carreteras". Contaminación del agua, el aire y el suelo . 2 (3): 387–392. Bibcode :1973WASP....2..387H. doi :10.1007/BF00159677. S2CID  109914430.
55. Stachowiak, Gwidon W.; Batchelor, Andrew William (2000). Tribología de ingeniería (2.ª ed.). Oxford: Butterworth-Heinemann. ISBN 978-0-7506-7304-4.
56. http://144.206.159.178/ft/200/607426/12614863.pdf ^{[ enlace muerto permanente ]}
57. http://www.rubberchemtechnol.org/resource/1/rctea4/v3/i1/p19_s1?isAuthorized=no ^{[ enlace muerto permanente ]}
58. "Neumáticos Schwalbe: resistencia a la rodadura".
59. Centro de información sobre bicicletas reclinadas y vehículos propulsados ​​por humanos
60. Oficina Nacional de Normas de EE. UU. p.? y Williams p.?
61. Roberts, "Efecto de la temperatura", p.59
62. Astakhov, pág. 74. Aunque Astakhov enumera estos componentes, no le da un nombre a la suma.
63. Шадур. Л. A. (editor). Вагоны (en ruso) (Vagones de ferrocarril). Москва, Транспорт, 1980. págs. 122 y figs. VI.1 pág. 123 VI.2 pág. 125
64. Association of American Railroads, Mechanical Division "Car and Locomotive Encyclopedia", Nueva York, Simmons-Boardman, 1974. Sección 14: "Cojinetes y muñones de ejes". Casi todos los anuncios de esta sección son de cojinetes de tipo cónico.
65. Астахов, figura 4.2, pág. 76
66. Estadísticas de los ferrocarriles de clase I en los Estados Unidos, años 1965 a 1975: Resumen estadístico. Washington DC, Asociación de Ferrocarriles Estadounidenses, Departamento de Economía y Finanzas. Véase la tabla de Amtrak, pág. 16. Para obtener las toneladas por pasajero, divida las toneladas-milla (incluidas las locomotoras) por las millas-pasajeros. Para obtener las toneladas brutas/toneladas netas, divida las toneladas-milla brutas (incluidas las locomotoras) (en la tabla de "estadísticas operativas" por las toneladas-millas de ingresos (de la tabla de "Tráfico de carga").

• Астахов П.Н. (en ruso) "Сопротивление движению железнодорожного подвижного состава" (Resistencia al movimiento del material rodante ferroviario) Труды ЦНИИ МПС (ISSN 0372-3305). Выпуск 311 (Vol.311). - Moscú: Tranvía, 1966. – 178 pp., registro permanente en la Universidad de California en Berkeley (en 2012, el texto completo estaba en Internet, pero en Estados Unidos estaba bloqueado)
• Деев В.В., Ильин Г.А., Афонин Г.С. (en ruso) "Тяга поездов" (Tracción de trenes) Учебное пособие. - М.: Транспорт, 1987. - 264 págs.
• Hay, William W. "Ingeniería ferroviaria" Nueva York, Wiley 1953
• Hersey, Mayo D. , "Rolling Friction" Transactions of the ASME , abril de 1969, págs. 260-275 y Journal of Lubrication Technology , enero de 1970, págs. 83-88 (un artículo dividido entre dos revistas) A excepción de la "Introducción histórica" ​​y un estudio de la literatura, se trata principalmente de pruebas de laboratorio de ruedas de hierro fundido de ferrocarriles mineros de diámetros de 8″ a 24 realizadas en la década de 1920 (casi medio siglo de retraso entre el experimento y la publicación).
• Hoerner, Sighard F., "Arrastre fluidodinámico", publicado por el autor, 1965. (El capítulo 12 es "Vehículos terrestres" e incluye resistencia al rodamiento (trenes, automóviles, camiones).)
• Roberts, GB, "Pérdida de potencia en los neumáticos", Conferencia Internacional del Caucho, Washington, DC 1959.
• Oficina Nacional de Normas de EE. UU., "Mecánica de neumáticos", Monografía n.° 132, 1969-1970.
• Williams, JA 'Tribología de ingeniería'. Oxford University Press, 1994.

Enlaces externos

• Resistencia a la rodadura y ahorro de combustible
• Temperatura vs resistencia a la rodadura
• Prueba de deslizamiento simple para medir Crr en automóviles y motocicletas
• Umbrales de resistencia a la rodadura