Giro peraltado

Inclination of road or surface other than flat

Un viraje peraltado (o viraje en pendiente ) es un viraje o cambio de dirección en el que el vehículo se inclina o se ladea, generalmente hacia el interior del viraje. En el caso de una carretera o un ferrocarril, esto suele deberse a que la plataforma de la carretera tiene una pendiente descendente transversal hacia el interior de la curva. El ángulo de inclinación es el ángulo en el que el vehículo está inclinado sobre su eje longitudinal con respecto a la horizontal.

Encender superficies planas

Si el ángulo de inclinación es cero, la superficie es plana y la fuerza normal es vertical hacia arriba. La única fuerza que mantiene al vehículo girando en su trayectoria es la fricción o tracción . Esta debe ser lo suficientemente grande como para proporcionar la fuerza centrípeta , una relación que se puede expresar como una desigualdad, suponiendo que el automóvil se desplaza en un círculo de radio : ${\displaystyle r}$

${\displaystyle \mu mg>{mv^{2} \over r}.}$

La expresión del lado derecho es la aceleración centrípeta multiplicada por la masa, la fuerza necesaria para girar el vehículo. El lado izquierdo es la fuerza de fricción máxima, que es igual al coeficiente de fricción multiplicado por la fuerza normal. Reordenando la velocidad máxima en curvas es ${\displaystyle \mu }$

${\displaystyle v<{\sqrt {r\mu g}}.}$

Tenga en cuenta que puede ser el coeficiente de fricción estática o dinámica. En el último caso, cuando el vehículo patina en una curva, la fricción está en su límite y las desigualdades se convierten en ecuaciones. Esto también ignora efectos como la carga aerodinámica , que puede aumentar la fuerza normal y la velocidad en las curvas. ${\displaystyle \mu }$

Curva peraltada sin fricción

Panel superior: Pelota en una pista circular peraltada que se mueve con velocidad constante ; Panel inferior: Fuerzas sobre la pelota. La fuerza resultante o neta sobre la pelota, que se obtiene mediante la suma vectorial de la fuerza normal ejercida por la carretera y la fuerza vertical debida a la gravedad, debe ser igual a la fuerza requerida para la aceleración centrípeta, determinada por la necesidad de recorrer una trayectoria circular. ${\displaystyle v}$

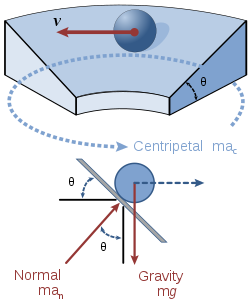
A diferencia de un vehículo que se desplaza a lo largo de un círculo plano, los bordes inclinados añaden una fuerza adicional que mantiene al vehículo en su trayectoria y evita que un automóvil sea "arrastrado hacia" o "empujado hacia fuera" del círculo (o que una rueda de ferrocarril se mueva lateralmente hasta casi rozar la pestaña de la rueda ). Esta fuerza es el componente horizontal de la fuerza normal del vehículo (N). En ausencia de fricción, la fuerza normal es la única que actúa sobre el vehículo en la dirección del centro del círculo. Por lo tanto, según la segunda ley de Newton, podemos establecer el componente horizontal de la fuerza normal igual a la masa multiplicada por la aceleración centrípeta: ^[1]

${\displaystyle {mv^{2} \over r}=N\sin \theta }$

Como no hay movimiento en la dirección vertical, la suma de todas las fuerzas verticales que actúan sobre el sistema debe ser cero. Por lo tanto, podemos establecer el componente vertical de la fuerza normal del vehículo igual a su peso: ^[1]

${\displaystyle N\cos \theta =mg}$

Resolviendo la ecuación anterior para la fuerza normal y sustituyendo este valor en nuestra ecuación anterior, obtenemos:

${\displaystyle {mv^{2} \over r}={mg\tan \theta }}$

Esto es equivalente a:

${\displaystyle {v^{2} \over r}={g\tan \theta }}$

Resolviendo la velocidad tenemos:

${\displaystyle v={\sqrt {rg\tan \theta }}}$

Esto proporciona la velocidad que, en ausencia de fricción y con un ángulo de inclinación y un radio de curvatura determinados , garantizará que el vehículo permanezca en su trayectoria designada. La magnitud de esta velocidad también se conoce como "velocidad nominal" (o "velocidad de equilibrio" para los ferrocarriles) de un giro o curva. ^[2] Observe que la velocidad nominal de la curva es la misma para todos los objetos masivos, y una curva que no esté inclinada tendrá una velocidad nominal de 0.

Curva peraltada con fricción

Una curva muy pronunciada en una rampa que conecta la Ruta Estatal 92 de California en dirección este con la Interestatal 880 en dirección norte en Hayward, California .

Los ciclistas toman una curva cerrada cuesta abajo en el Beanpot Criterium en la Universidad Tufts.

Al considerar los efectos de la fricción en el sistema, una vez más debemos tener en cuenta en qué dirección apunta la fuerza de fricción. Al calcular una velocidad máxima para nuestro automóvil, la fricción apuntará hacia abajo de la pendiente y hacia el centro del círculo. Por lo tanto, debemos sumar el componente horizontal de la fricción al de la fuerza normal. La suma de estas dos fuerzas es nuestra nueva fuerza neta en la dirección del centro de la curva (la fuerza centrípeta):

${\displaystyle \underbrace {{mv^{2} \over r}=N\sin \theta } _{\text{Frictionless formula}}+\underbrace {\mu _{s}N\cos \theta } _{\text{Friction term}}}$

Una vez más, no hay movimiento en la dirección vertical, lo que nos permite igualar entre sí todas las fuerzas verticales opuestas. Estas fuerzas incluyen el componente vertical de la fuerza normal que apunta hacia arriba y tanto el peso del automóvil como el componente vertical de fricción que apunta hacia abajo:

${\displaystyle \underbrace {N\cos \theta =mg} _{\text{Frictionless formula}}+\underbrace {\mu _{s}N\sin \theta } _{\text{Friction term}}}$

Al resolver la ecuación anterior para la masa y sustituir este valor en nuestra ecuación anterior obtenemos:

${\displaystyle {\frac {{\frac {N\cos \theta -\mu _{s}N\sin \theta }{g}}v^{2}}{r}}=N\sin \theta +\mu _{s}N\cos \theta }$

Resolviendo obtenemos: ${\displaystyle v}$

${\displaystyle v_{\mathrm {max} }={\sqrt {rg\left(\sin \theta +\mu _{s}\cos \theta \right) \over \cos \theta -\mu _{s}\sin \theta }}={\sqrt {rg{\frac {\tan \theta +\mu _{s}}{1-\mu _{s}\tan \theta }}}}={\sqrt {rg\tan(\theta +\theta _{\mathrm {crit} })}}}$

Donde es el ángulo crítico, tal que . Esta ecuación proporciona la velocidad máxima para el automóvil con el ángulo de inclinación, el coeficiente de fricción estática y el radio de curvatura dados. Mediante un análisis similar de la velocidad mínima, se obtiene la siguiente ecuación: ${\displaystyle \theta _{\mathrm {crit} }}$ ${\displaystyle \tan \theta _{\mathrm {crit} }=\mu _{s}}$

${\displaystyle v_{\mathrm {min} }={\sqrt {rg\left(\sin \theta -\mu _{s}\cos \theta \right) \over \cos \theta +\mu _{s}\sin \theta }}={\sqrt {rg{\frac {\tan \theta -\mu _{s}}{1+\mu _{s}\tan \theta }}}}={\sqrt {rg\tan(\theta -\theta _{\mathrm {crit} })}}}$

Aviso

${\displaystyle {\frac {v_{\mathrm {min} }}{v_{\mathrm {max} }}}={\sqrt {\frac {\tan(\theta -\theta _{\mathrm {crit} })}{\tan(\theta +\theta _{\mathrm {crit} })}}}}$

La diferencia en este último análisis surge al considerar la dirección de la fricción para la velocidad mínima del automóvil (hacia el exterior del círculo). En consecuencia, se realizan operaciones opuestas al insertar la fricción en las ecuaciones para fuerzas en las direcciones centrípeta y vertical.

Las curvas mal peraltadas aumentan el riesgo de salida de la calzada y de colisiones frontales. Se puede esperar que una deficiencia del 2% en el peralte (por ejemplo, un 4% de peralte en una curva que debería tener un 6%) aumente la frecuencia de colisiones en un 6%, y una deficiencia del 5% la aumentará en un 15%. ^[3] Hasta ahora, los ingenieros de carreteras no han tenido herramientas eficientes para identificar curvas mal peraltadas y diseñar acciones de mitigación pertinentes en la carretera. Un perfilógrafo moderno puede proporcionar datos tanto de la curvatura de la carretera como de la pendiente transversal (ángulo de inclinación). En el proyecto EU Roadex III se desarrolló una demostración práctica de cómo evaluar curvas mal peraltadas. Consulte el documento de referencia vinculado a continuación.

Giro peraltado en aeronáutica

Douglas DC-3 se inclina para hacer un giro a la izquierda.

Cuando una aeronave de ala fija está realizando un viraje (cambiando su dirección), la aeronave debe inclinarse hasta una posición inclinada de modo que sus alas estén en ángulo hacia la dirección deseada del viraje. Una vez completado el viraje, la aeronave debe volver a la posición de alas niveladas para reanudar el vuelo recto. ^[4]

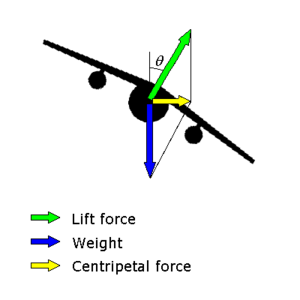
Cuando un vehículo en movimiento realiza un giro, es necesario que las fuerzas que actúan sobre el vehículo se sumen para formar una fuerza neta hacia adentro, para provocar una aceleración centrípeta . En el caso de un avión que realiza un giro, la fuerza que provoca la aceleración centrípeta es el componente horizontal de la sustentación que actúa sobre el avión.

En vuelo recto y nivelado, la sustentación que actúa sobre el avión actúa verticalmente hacia arriba para contrarrestar el peso del avión que actúa hacia abajo. Si el avión va a continuar en vuelo nivelado (es decir, a una altitud constante ), el componente vertical debe seguir siendo igual al peso del avión y, por lo tanto, el piloto debe tirar hacia atrás de la palanca para aplicar los elevadores para inclinar el morro hacia arriba y, por lo tanto, aumentar el ángulo de ataque , lo que genera un aumento en la sustentación del ala. La sustentación total (ahora en ángulo) es mayor que el peso del avión. El exceso de sustentación es el componente horizontal de la sustentación total, que es la fuerza neta que hace que el avión acelere hacia adentro y ejecute el viraje.

Diagrama vectorial que muestra la sustentación y el peso que actúan sobre una aeronave de ala fija durante un viraje inclinado. La fuerza amarilla que se muestra representa la fuerza resultante neta que causa la aceleración centrípeta.

Porque la aceleración centrípeta es:

${\displaystyle a={v^{2} \over r}}$

Durante un viraje equilibrado en el que el ángulo de inclinación es 1, la sustentación actúa en un ángulo que se aleja de la vertical. Resulta útil dividir la sustentación en un componente vertical y un componente horizontal. ${\displaystyle \theta }$ ${\displaystyle \theta }$

La segunda ley de Newton en dirección horizontal se puede expresar matemáticamente como:

${\displaystyle L\sin \theta ={mv^{2} \over r}}$

dónde:

${\displaystyle L}$¿Es la sustentación la que actúa sobre el avión?

${\displaystyle \theta }$es el ángulo de inclinación del avión

${\displaystyle m}$es la masa de la aeronave

${\displaystyle v}$es la verdadera velocidad aerodinámica del avión

${\displaystyle r}$es el radio del giro

En vuelo recto y nivelado, la sustentación es igual al peso de la aeronave. En vuelo con viraje, la sustentación supera el peso de la aeronave y es igual al peso de la aeronave ( ) dividido por el coseno del ángulo de inclinación: ${\displaystyle g}$

${\displaystyle L={mg \over {\cos \theta }}}$

¿Dónde está la intensidad del campo gravitacional? ${\displaystyle g}$

Ahora se puede calcular el radio del giro: ^[5]

${\displaystyle r={v^{2} \over {g\tan \theta }}}$

Esta fórmula demuestra que el radio de giro es proporcional al cuadrado de la velocidad aerodinámica real del avión . A mayor velocidad aerodinámica, el radio de giro es mayor y, a menor velocidad aerodinámica, menor.

Esta fórmula también muestra que el radio de giro disminuye con el ángulo de inclinación. Con un ángulo de inclinación más alto, el radio de giro es menor y con un ángulo de inclinación más bajo, el radio es mayor.

En un viraje inclinado a una altitud constante, el factor de carga es igual a . Podemos ver que el factor de carga en vuelo recto y nivelado es , ya que , y para generar suficiente sustentación para mantener una altitud constante, el factor de carga debe acercarse al infinito a medida que el ángulo de inclinación se acerca y se acerca a . Esto es físicamente imposible, porque las limitaciones estructurales de la aeronave o la resistencia física de los ocupantes se superarán mucho antes de eso. ${\displaystyle {\frac {1}{\cos \theta }}}$ ${\displaystyle 1}$ ${\displaystyle \cos(0)=1}$ ${\displaystyle 90^{\circ }}$ ${\displaystyle \cos \theta }$ ${\displaystyle 0}$

Giro peraltado en atletismo

La mayoría de las pistas cubiertas tienen curvas peraltadas, ya que son más pequeñas que las pistas al aire libre . Las curvas cerradas de estas pistas pequeñas suelen estar peraltadas para permitir que los atletas se inclinen hacia adentro y neutralicen la fuerza centrífuga mientras corren por la curva; la inclinación es especialmente notoria en las pruebas de velocidad . ^[6]

• 
  Los velocistas se inclinan para tomar una curva en una pista cubierta peraltada

Véase también

• Ángulo de inclinación
• Peralte (carretera/ferrocarril)
• Fuerza de Coriolis (percepción)
• Fuerza centrípeta
• fuerza g
• Carreras en pista ovalada

Referencias

1. Serway, pág. 143
2. Beer, Ferdinand P. ; Johnston, E. Russell (11 de julio de 2003). Mecánica vectorial para ingenieros: dinámica . Ciencia/Ingeniería/Matemáticas (7.ª ed.). McGraw-Hill. ISBN 978-0-07-293079-5.
3. DW Harwood, et al., Predicción del desempeño de seguridad esperado de las carreteras rurales de dos carriles , Turner-Fairbank Highway Research Center, McLean, Virginia, diciembre de 2000, página 39, https://www.fhwa.dot.gov/publications/research/safety/99207/99207.pdf
4. Administración Federal de Aviación (2007). Enciclopedia de conocimientos aeronáuticos para pilotos. Oklahoma City, OK: Skyhorse Publishing Inc. Figura 3-21. ISBN 978-1-60239-034-8.
5. Clancy, LJ, Ecuación 14.9
6. Greene, Peter (febrero de 1987). "Correr con curvas peraltadas". Journal of Biomechanics . 20 (7): 667–80. doi :10.1016/0021-9290(87)90033-9. PMID  3654665.

Lectura adicional

Vehículos de superficie

• Serway, Raymond. Física para científicos e ingenieros. Cengage Learning, 2010.
• Cuestiones de salud y seguridad, proyecto Roadex III de la UE sobre cuestiones de salud y seguridad planteadas por redes de carreteras en mal estado.

Aeronáutica

• Kermode, AC (1972) Mecánica del vuelo , Capítulo 8, 10.ª edición, Longman Group Limited, Londres ISBN 0-582-23740-8 
• Clancy, LJ (1975), Aerodinámica , Pitman Publishing Limited, Londres ISBN 0-273-01120-0 
• Hurt, HH Jr, (1960), Aerodinámica para aviadores navales , una reimpresión de National Flightshop, Florida

Enlaces externos

Vehículos de superficie

• http://hyperphysics.phy-astr.gsu.edu/hbase/mechanics/imgmech/carbank.gif
• https://web.archive.org/web/20051222173550/http://whitts.alioth.net/
• http://www.batesville.k12.in.us/physics/PHYNET/Mechanics/Circular%20Motion/banked_no_friction.htm

Aeronáutica

• NASA: Orientación sobre los giros en pendiente
• aerospaceweb.org: Ángulo de inclinación y G (matemáticas)
• Manual de conocimientos aeronáuticos para pilotos

https://edu-physics.com/2021/05/08/how-banking-of-road-will-help-the-vehicle-to-travel-along-a-circular-path-2/