Desigualdad isoperimétrica

Desigualdad geométrica que establece un límite inferior en el área de superficie de un conjunto dado su volumen

En matemáticas, la desigualdad isoperimétrica es una desigualdad geométrica que involucra el perímetro de un conjunto y su volumen. En el espacio -dimensional, la desigualdad limita el área de superficie o perímetro de un conjunto por su volumen , ${\displaystyle n}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle \operatorname {per} (S)}$ ${\displaystyle S\subset \mathbb {R} ^{n}}$ ${\displaystyle \operatorname {vol} (S)}$

${\displaystyle \operatorname {per} (S)\geq n\operatorname {vol} (S)^{(n-1)/n}\,\operatorname {vol} (B_{1})^{1/n}}$,

donde es una esfera unitaria . La igualdad se cumple sólo cuando es una esfera en . ${\displaystyle B_{1}\subset \mathbb {R} ^{n}}$ ${\displaystyle S}$ ${\displaystyle \mathbb {R} ^{n}}$

En un plano, es decir, cuando , la desigualdad isoperimétrica relaciona el cuadrado de la circunferencia de una curva cerrada y el área de una región plana que encierra. Isoperimétrico significa literalmente "que tiene el mismo perímetro ". Específicamente en , la desigualdad isoperimétrica establece, para la longitud L de una curva cerrada y el área A de la región plana que encierra, que ${\displaystyle n=2}$ ${\displaystyle \mathbb {R} ^{2}}$

${\displaystyle L^{2}\geq 4\pi A,}$

y esa igualdad se cumple si y sólo si la curva es un círculo.

El problema isoperimétrico consiste en determinar una figura plana de la mayor área posible cuyo límite tenga una longitud especificada. ^{[1] El} problema de Dido, estrechamente relacionado , pide una región del área máxima delimitada por una línea recta y un arco curvilíneo cuyos puntos finales pertenecen a esa línea. Lleva el nombre de Dido , la legendaria fundadora y primera reina de Cartago . La solución al problema isoperimétrico viene dada por una circunferencia y ya era conocida en la Antigua Grecia . Sin embargo, la primera prueba matemática rigurosa de este hecho no se obtuvo hasta el siglo XIX. Desde entonces se han encontrado muchas otras pruebas.

El problema isoperimétrico se ha extendido de múltiples maneras, por ejemplo, a curvas en superficies y regiones en espacios de dimensiones superiores. Quizás la manifestación física más familiar de la desigualdad isoperimétrica tridimensional es la forma de una gota de agua. Es decir, una gota normalmente adoptará una forma redonda simétrica. Dado que la cantidad de agua en una gota es fija, la tensión superficial fuerza a la gota a adoptar una forma que minimice su área de superficie, es decir, una esfera redonda.

El problema isoperimétrico en el avión.

Si una región no es convexa, se puede "invertir" una "abolladura" en su límite para aumentar el área de la región manteniendo el perímetro sin cambios.

Una forma alargada se puede hacer más redonda manteniendo fijo su perímetro y aumentando su área.

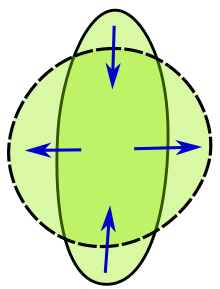
El problema isoperimétrico clásico se remonta a la antigüedad. ^[2] El problema se puede plantear de la siguiente manera: Entre todas las curvas cerradas en el plano de perímetro fijo, ¿qué curva (si la hay) maximiza el área de su región cerrada? Se puede demostrar que esta pregunta es equivalente al siguiente problema: entre todas las curvas cerradas en el plano que encierra un área fija, ¿qué curva (si la hay) minimiza el perímetro?

Este problema está conceptualmente relacionado con el principio de mínima acción en física , en el sentido de que puede reformularse: ¿cuál es el principio de acción que encierra la mayor área, con la mayor economía de esfuerzo? El filósofo y científico del siglo XV, el cardenal Nicolás de Cusa , consideraba que la acción rotacional , el proceso mediante el cual se genera un círculo , era el reflejo más directo, en el ámbito de las impresiones sensoriales, del proceso mediante el cual se crea el universo. El astrónomo y astrólogo alemán Johannes Kepler invocó el principio isoperimétrico al discutir la morfología del sistema solar, en Mysterium Cosmographicum ( El misterio sagrado del cosmos , 1596).

Aunque el círculo parece ser una solución obvia al problema, demostrar este hecho es bastante difícil. El primer avance hacia la solución lo realizó el geómetra suizo Jakob Steiner en 1838, utilizando un método geométrico posteriormente denominado simetrización de Steiner . ^[3] Steiner demostró que si existía una solución, entonces debía ser el círculo. La demostración de Steiner fue completada más tarde por varios otros matemáticos.

Steiner comienza con algunas construcciones geométricas de fácil comprensión; por ejemplo, se puede demostrar que cualquier curva cerrada que encierre una región que no sea completamente convexa puede modificarse para incluir más área, "invirtiendo" las áreas cóncavas para que se vuelvan convexas. Además, se puede demostrar que cualquier curva cerrada que no sea completamente simétrica puede "inclinarse" para que incluya más área. La única forma que es perfectamente convexa y simétrica es el círculo, aunque esto, en sí mismo, no representa una prueba rigurosa del teorema isoperimétrico (ver enlaces externos).

En un avión

La solución al problema isoperimétrico generalmente se expresa en forma de una desigualdad que relaciona la longitud L de una curva cerrada y el área A de la región plana que encierra. La desigualdad isoperimétrica establece que

${\displaystyle 4\pi A\leq L^{2},}$

y que la igualdad se cumple si y sólo si la curva es un círculo. El área de un disco de radio R es πR ² y la circunferencia del círculo es 2 πR , por lo que ambos lados de la desigualdad son iguales a 4 π ² R ² en este caso.

Se han encontrado decenas de pruebas de la desigualdad isoperimétrica. En 1902, Hurwitz publicó una breve prueba utilizando la serie de Fourier que se aplica a curvas rectificables arbitrarias (que no se supone que sean suaves). E. Schmidt realizó en 1938 una elegante prueba directa basada en la comparación de una curva cerrada simple y suave con un círculo apropiado. Utiliza únicamente la fórmula de la longitud del arco , expresión para el área de una región plana del teorema de Green y el método de Cauchy. Desigualdad de Schwarz .

Para una curva cerrada dada, el cociente isoperimétrico se define como la relación entre su área y la del círculo que tiene el mismo perímetro. Esto es igual a

${\displaystyle Q={\frac {4\pi A}{L^{2}}}}$

y la desigualdad isoperimétrica dice que Q ≤ 1. De manera equivalente, la relación isoperimétrica L ² / A es al menos 4 π para cada curva.

El cociente isoperimétrico de un n -gón regular es

${\displaystyle Q_{n}={\frac {\pi }{n\tan(\pi /n)}}.}$

Sea una curva cerrada convexa regular suave. Entonces la desigualdad isoperimétrica mejorada establece lo siguiente ${\displaystyle C}$

${\displaystyle L^{2}\geqslant 4\pi A+8\pi \left|{\widetilde {A}}_{0.5}\right|,}$

donde denotan la longitud de , el área de la región delimitada por y el área orientada de la cáustica de Wigner de , respectivamente, y la igualdad se cumple si y solo si es una curva de ancho constante . ^[4] ${\displaystyle L,A,{\widetilde {A}}_{0.5}}$ ${\displaystyle C}$ ${\displaystyle C}$ ${\displaystyle C}$ ${\displaystyle C}$

en una esfera

Sea C una curva cerrada simple en una esfera de radio 1. Denotemos por L la longitud de C y por A el área encerrada por C. La desigualdad isoperimétrica esférica establece que

${\displaystyle L^{2}\geq A(4\pi -A),}$

y que la igualdad se cumple si y sólo si la curva es un círculo. De hecho, existen dos formas de medir el área esférica encerrada por una curva cerrada simple, pero la desigualdad es simétrica con respecto a tomar el complemento.

Esta desigualdad fue descubierta por Paul Lévy (1919) quien también la extendió a dimensiones superiores y superficies generales. ^[5]

En el caso más general de radio arbitrario R , se sabe ^[6] que

${\displaystyle L^{2}\geq 4\pi A-{\frac {A^{2}}{R^{2}}}.}$

en r n

La desigualdad isoperimétrica establece que una esfera tiene la superficie más pequeña por volumen dado. Dado un conjunto acotado con área de superficie y volumen , la desigualdad isoperimétrica establece ${\displaystyle S\subset \mathbb {R} ^{n}}$ ${\displaystyle \operatorname {per} (S)}$ ${\displaystyle \operatorname {vol} (S)}$

${\displaystyle \operatorname {per} (S)\geq n\operatorname {vol} (S)^{(n-1)/n}\,\operatorname {vol} (B_{1})^{1/n},}$

¿ Dónde está una bola unitaria ? La igualdad se cumple cuando hay una pelota en . Bajo restricciones adicionales en el conjunto (como convexidad , regularidad , límite suave ), la igualdad se cumple solo para una bola. Pero en general la situación es más complicada. El resultado relevante de Schmidt (1949, sección 20.7) (para una prueba más sencilla, véase Baebler (1957)) se aclara en Hadwiger (1957, sección 5.2.5) de la siguiente manera. Un conjunto extremo consta de una bola y una "corona" que no contribuye ni al volumen ni a la superficie. Es decir, la igualdad se cumple para un conjunto compacto si y sólo si contiene una bola cerrada tal que y. Por ejemplo, la "corona" puede ser una curva. ${\displaystyle B_{1}\subset \mathbb {R} ^{n}}$ ${\displaystyle S}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle S}$ ${\displaystyle S}$ ${\displaystyle B}$ ${\displaystyle \operatorname {vol} (B)=\operatorname {vol} (S)}$ ${\displaystyle \operatorname {per} (B)=\operatorname {per} (S).}$

La prueba de la desigualdad se sigue directamente de la desigualdad de Brunn-Minkowski entre un conjunto y una bola con radio , es decir . Llevando la desigualdad de Brunn-Minkowski a la potencia , restando de ambos lados, dividiéndolos por y tomando el límite como (Osserman (1978); Federer (1969, §3.2.43)). ${\displaystyle S}$ ${\displaystyle \epsilon }$ ${\displaystyle B_{\epsilon }=\epsilon B_{1}}$ ${\displaystyle n}$ ${\displaystyle \operatorname {vol} (S)}$ ${\displaystyle \epsilon }$ ${\displaystyle \epsilon \to 0.}$

En total generalidad (Federer 1969, §3.2.43), la desigualdad isoperimétrica establece que para cualquier conjunto cuyo cierre tenga medida de Lebesgue finita ${\displaystyle S\subset \mathbb {R} ^{n}}$

${\displaystyle n\,\omega _{n}^{1/n}L^{n}({\bar {S}})^{(n-1)/n}\leq M_{*}^{n-1}(\partial S)}$

donde es el contenido de Minkowski ( n -1)-dimensional , L ⁿ es la medida de Lebesgue n -dimensional y ω _n es el volumen de la bola unitaria en . Si el límite de S es rectificable , entonces el contenido de Minkowski es la medida de Hausdorff ( n -1)-dimensional . ${\displaystyle M_{*}^{n-1}}$ ${\displaystyle \mathbb {R} ^{n}}$

La desigualdad isoperimétrica n -dimensional es equivalente (para dominios suficientemente suaves) a la desigualdad de Sobolev con constante óptima: ${\displaystyle \mathbb {R} ^{n}}$

${\displaystyle \left(\int _{\mathbb {R} ^{n}}|u|^{n/(n-1)}\right)^{(n-1)/n}\leq n^{-1}\omega _{n}^{-1/n}\int _{\mathbb {R} ^{n}}|\nabla u|}$

para todos . ${\displaystyle u\in W^{1,1}(\mathbb {R} ^{n})}$

En variedades Hadamard

Los colectores Hadamard son colectores completos simplemente conectados con curvatura no positiva. Así generalizan el espacio euclidiano , que es una variedad de Hadamard con curvatura cero. En los años 1970 y principios de los 80, Thierry Aubin , Misha Gromov , Yuri Burago y Viktor Zalgaller conjeturaron que la desigualdad isoperimétrica euclidiana ${\displaystyle \mathbb {R} ^{n}}$

${\displaystyle \operatorname {per} (S)\geq n\operatorname {vol} (S)^{(n-1)/n}\operatorname {vol} (B_{1})^{1/n}}$

es válido para conjuntos acotados en variedades de Hadamard, lo que se conoce como la conjetura de Cartan-Hadamard . En la dimensión 2 esto ya había sido establecido en 1926 por André Weil , que en ese momento era alumno de Hadamard . En las dimensiones 3 y 4, la conjetura fue probada por Bruce Kleiner en 1992 y Chris Croke en 1984, respectivamente. ${\displaystyle S}$

En un espacio de medida métrica

La mayor parte del trabajo sobre problemas isoperimétricos se ha realizado en el contexto de regiones suaves en espacios euclidianos o, más generalmente, en variedades de Riemann . Sin embargo, el problema isoperimétrico se puede formular con mucha mayor generalidad, utilizando la noción de contenido de Minkowski . Sea un espacio de medidas métricas : X es un espacio métrico con métrica d y μ es una medida de Borel en X. La medida límite , o contenido de Minkowski , de un subconjunto mensurable A de X se define como el límite inf. ${\displaystyle (X,\mu ,d)}$

${\displaystyle \mu ^{+}(A)=\liminf _{\varepsilon \to 0+}{\frac {\mu (A_{\varepsilon })-\mu (A)}{\varepsilon }},}$

dónde

${\displaystyle A_{\varepsilon }=\{x\in X|d(x,A)\leq \varepsilon \}}$

es la extensión ε de A .

El problema isoperimétrico en X pregunta qué tan pequeño puede ser para un μ ( A ) dado. Si X es el plano euclidiano con la distancia habitual y la medida de Lebesgue , entonces esta pregunta generaliza el problema isoperimétrico clásico a regiones planas cuyos límites no son necesariamente suaves, aunque la respuesta resulta ser la misma. ${\displaystyle \mu ^{+}(A)}$

La función

${\displaystyle I(a)=\inf\{\mu ^{+}(A)|\mu (A)=a\}}$

Se llama perfil isoperimétrico del espacio de medidas métricas . Se han estudiado perfiles isoperimétricos para gráficos de Cayley de grupos discretos y para clases especiales de variedades de Riemann (donde normalmente sólo se consideran regiones A con límite regular). ${\displaystyle (X,\mu ,d)}$

Para gráficos

En teoría de grafos , las desigualdades isoperimétricas están en el centro del estudio de los gráficos de expansión , que son gráficos dispersos que tienen fuertes propiedades de conectividad. Las construcciones expansoras han generado investigaciones en matemáticas puras y aplicadas, con varias aplicaciones a la teoría de la complejidad , el diseño de redes informáticas robustas y la teoría de códigos de corrección de errores . ^[7]

Las desigualdades isoperimétricas para gráficos relacionan el tamaño de los subconjuntos de vértices con el tamaño de su límite, que generalmente se mide por el número de aristas que salen del subconjunto (expansión de aristas) o por el número de vértices vecinos (expansión de vértices). Para una gráfica y un número , los siguientes son dos parámetros isoperimétricos estándar para gráficas. ^[8] ${\displaystyle G}$ ${\displaystyle k}$

• El parámetro isoperimétrico del borde:
  $${\displaystyle \Phi _{E}(G,k)=\min _{S\subseteq V}\left\{|E(S,{\overline {S}})|:|S|=k\right\}}$$
• El parámetro isoperimétrico del vértice:
  $${\displaystyle \Phi _{V}(G,k)=\min _{S\subseteq V}\left\{|\Gamma (S)\setminus S|:|S|=k\right\}}$$

Aquí denota el conjunto de aristas que salen y denota el conjunto de vértices que tienen un vecino . El problema isoperimétrico consiste en comprender cómo se comportan los parámetros y para familias naturales de gráficas. ${\displaystyle E(S,{\overline {S}})}$ ${\displaystyle S}$ ${\displaystyle \Gamma (S)}$ ${\displaystyle S}$ ${\displaystyle \Phi _{E}}$ ${\displaystyle \Phi _{V}}$

Ejemplo: desigualdades isoperimétricas para hipercubos

El hipercubo bidimensional es el gráfico cuyos vértices son todos vectores booleanos de longitud , es decir, el conjunto . Dos de estos vectores están conectados por una arista si son iguales hasta un solo cambio de bit, es decir, su distancia de Hamming es exactamente uno. Las siguientes son las desigualdades isoperimétricas del hipercubo booleano. ^[9] ${\displaystyle d}$ ${\displaystyle Q_{d}}$ ${\displaystyle d}$ ${\displaystyle \{0,1\}^{d}}$ ${\displaystyle Q_{d}}$

Desigualdad isoperimétrica de borde

La desigualdad isoperimétrica de arista del hipercubo es . Este límite es estrecho, como lo demuestra cada conjunto que es el conjunto de vértices de cualquier subcubo de . ${\displaystyle \Phi _{E}(Q_{d},k)\geq k(d-\log _{2}k)}$ ${\displaystyle S}$ ${\displaystyle Q_{d}}$

Desigualdad isoperimétrica de vértice

El teorema de Harper ^[10] dice que las bolas de Hamming tienen el límite de vértice más pequeño entre todos los conjuntos de un tamaño determinado. Las bolas de Hamming son conjuntos que contienen todos los puntos de peso de Hamming como máximo y ningún punto de peso de Hamming mayor que el de algún número entero . Este teorema implica que cualquier conjunto con ${\displaystyle r}$ ${\displaystyle r+1}$ ${\displaystyle r}$ ${\displaystyle S\subseteq V}$

${\displaystyle |S|\geq \sum _{i=0}^{r}{d \choose i}}$

satisface

${\displaystyle |S\cup \Gamma (S)|\geq \sum _{i=0}^{r+1}{d \choose i}.}$^[11]

Como caso especial, considere los tamaños establecidos del formulario. ${\displaystyle k=|S|}$

${\displaystyle k={d \choose 0}+{d \choose 1}+\dots +{d \choose r}}$

para algún número entero . Entonces lo anterior implica que el parámetro isoperimétrico del vértice exacto es ${\displaystyle r}$

${\displaystyle \Phi _{V}(Q_{d},k)={d \choose r+1}.}$^[12]

Desigualdad isoperimétrica para triángulos

La desigualdad isoperimétrica para triángulos en términos de perímetro p y área T establece que ^[13]

${\displaystyle p^{2}\geq 12{\sqrt {3}}\cdot T,}$

con igualdad para el triángulo equilátero . Esto está implícito, a través de la desigualdad AM-GM , por una desigualdad más fuerte que también se ha denominado desigualdad isoperimétrica para triángulos: ^[14]

${\displaystyle T\leq {\frac {\sqrt {3}}{4}}(abc)^{2/3}.}$

Ver también

• Portal de matemáticas

• Teorema de Blaschke-Lebesgue
• Problema de Chaplygin
• Flujo de acortamiento de curvas
• Gráfico de expansión
• Desigualdad isoperimétrica gaussiana
• Dimensión isoperimétrica
• punto isoperimétrico
• Lista de desigualdades triangulares
• Teorema del separador plano
• Volumen mixto
• Problema de Chaplygin : el problema isoperimétrico es un caso de velocidad del viento cero del problema de Chaplygin

Notas

1. Blåsjö, Viktor (2005). "La evolución del problema isoperimétrico". América. Matemáticas. Mensual . 112 (6): 526–566. doi :10.2307/30037526. JSTOR  30037526.
2. Olmo, Carlos Beltrán, Irene (4 de enero de 2021). "Sobre mates y mitos". El País (en español) . Consultado el 14 de enero de 2021 .{{cite web}}: CS1 maint: multiple names: authors list (link)
3. J. Steiner, Einfacher Beweis der isoperimetrischen Hauptsätze , J. reine angew Math. 18 , (1838), págs. 281–296; y Gesammelte Werke vol. 2, págs. 77–91, Reimer, Berlín, (1882).
4. Zwierzyński, Michał (2016). "La desigualdad isoperimétrica mejorada y la cáustica de Wigner de los óvalos planos". J. Matemáticas. Anal. Aplica . 442 (2): 726–739. arXiv : 1512.06684 . doi :10.1016/j.jmaa.2016.05.016. S2CID  119708226.
5. Gromov, Mikhail; Pansu, Pierre (2006). "Apéndice C. Desigualdad isoperimétrica de Paul Levy". Estructuras métricas para espacios riemannianos y no riemannianos . Clásicos modernos de Birkhäuser. Dordrecht: Springer. pag. 519.ISBN​ 9780817645830.
6. Osserman, Robert . "La desigualdad isoperimétrica". Boletín de la Sociedad Estadounidense de Matemáticas. 84,6 (1978) http://www.ams.org/journals/bull/1978-84-06/S0002-9904-1978-14553-4/S0002-9904-1978-14553-4.pdf
7. Hoory, Linial y Widgerson (2006)
8. Definiciones 4.2 y 4.3 de Hoory, Linial & Widgerson (2006)
9. Véase Bollobás (1986) y la Sección 4 en Hoory, Linial & Widgerson (2006)
10. Cfr. Calabró (2004) o Bollobás (1986)
11. cf. Líder (1991)
12. También indicado en Hoory, Linial y Widgerson (2006)
13. Chakerian, GD "Una visión distorsionada de la geometría". Cap. 7 en Mathematical Plums (R. Honsberger, editor). Washington, DC: Asociación Matemática de América, 1979: 147.
14. Dragutin Svrtan y Darko Veljan, "Versiones no euclidianas de algunas desigualdades clásicas del triángulo", Forum Geometriorum 12, 2012, 197-209. http://forumgeom.fau.edu/FG2012volume12/FG201217.pdf

Referencias

• Blaschke y Leichtweiß, Elementare Differentialgeometrie (en alemán), 5ª edición, completamente revisada por K. Leichtweiß. Die Grundlehren der mathematischen Wissenschaften, Banda 1. Springer-Verlag , Nueva York Heidelberg Berlín, 1973 ISBN 0-387-05889-3 
• Bollobás, Béla (1986). Combinatoria: sistemas de conjuntos, hipergrafos, familias de vectores y probabilidad combinatoria . Prensa de la Universidad de Cambridge. ISBN 978-0-521-33703-8.
• Burago (2001) [1994], "Desigualdad isoperimétrica", Enciclopedia de Matemáticas , EMS Press
• Calabro, Chris (2004). "Teorema de Harper" (PDF) . Consultado el 8 de febrero de 2011 .
• Capogna, Luca; Donatella Danielli; Scott Pauls; Jeremy Tyson (2007). Introducción al grupo de Heisenberg y al problema isoperimétrico subriemanniano . Birkhäuser Verlag . ISBN 978-3-7643-8132-5.
• Fenchel, Werner ; Bonnesen, Tommy (1934). Theorie der konvexen Körper . Ergebnisse der Mathematik und ihrer Grenzgebiete. vol. 3. Berlín: 1. Verlag von Julius Springer.
• Fenchel, Werner ; Bonnesen, Tommy (1987). Teoría de los cuerpos convexos . Moscú, Idaho: L. Boron, C. Christenson y B. Smith. Asociados BCS. ISBN 9780914351023.
• Federer, Herbert (1969). Teoría de la medida geométrica . Springer-Verlag. ISBN 3-540-60656-4..
• Gromov, M .: "La desigualdad isoperimétrica de Paul Levy". Apéndice C en Estructuras métricas para espacios riemannianos y no riemannianos . Basado en el original francés de 1981. Con apéndices de M. Katz, P. Pansu y S. Semmes. Traducido del francés por Sean Michael Bates. Progreso en Matemáticas, 152. Birkhäuser Boston, Inc., Boston, Massachusetts, 1999.
• Hadwiger, Hugo (1957). Vorlesungen über Inhalt, Oberfläche und Isoperimetrie . Springer-Verlag..
• Hoory, Shlomo; Linial, Nathan ; Widgerson, Avi (2006). «Gráficos expansores y sus aplicaciones» (PDF) . Boletín de la Sociedad Matemática Estadounidense . Series nuevas. 43 (4): 439–561. doi : 10.1090/S0273-0979-06-01126-8 .
• Líder, Imre (1991). "Desigualdades isoperimétricas discretas". Actas de simposios en matemáticas aplicadas . vol. 44, págs. 57–80.
• Osserman, Robert (1978). "La desigualdad isoperimétrica". Toro. América. Matemáticas. Soc . 84 (6): 1182-1238. doi : 10.1090/S0002-9904-1978-14553-4 ..
• Zwierzyński, Michał (2016). "La desigualdad isoperimétrica mejorada y la cáustica de Wigner de los óvalos planos". J. Matemáticas. Anal. Aplica . 442 (2): 726–739. arXiv : 1512.06684 . doi :10.1016/j.jmaa.2016.05.016. S2CID  119708226.
• Schmidt, Erhard (1949). "Die Brunn-Minkowskische Ungleichung und ihr Spiegelbild sowie die isoperimetrische Eigenschaft der Hugel in der euklidischen und nichteuklidischen Geometrie. II". Matemáticas. Nachr . 2 (3–4): 171–244. doi :10.1002/mana.19490020308..
• Baebler, F. (1957). "El problema isoperimétrico". Arco. Matemáticas. (Basilea) . 8 : 52–65. doi :10.1007/BF01898439. S2CID  123704157..

enlaces externos

• Historia del problema isoperimétrico en la convergencia
• Treiberg: varias pruebas de la desigualdad isoperimétrica
• Teorema isoperimétrico al cortar el nudo