
En economía , una caja de Edgeworth, a veces denominada caja de Edgeworth-Bowley, es una representación gráfica de un mercado con sólo dos mercancías, X e Y , y dos consumidores. Las dimensiones de la caja son las cantidades totales Ω x y Ω y de los dos bienes.
Que los consumidores sean Octavio y Abby. La esquina superior derecha del cuadro representa la asignación en la que Octavio posee todos los bienes, mientras que la esquina inferior izquierda corresponde a la propiedad completa de Abby. Los puntos dentro del cuadro representan formas de distribuir los bienes entre los dos consumidores.
El comportamiento del mercado estará determinado por las curvas de indiferencia de los consumidores . Las curvas azules en el diagrama representan curvas de indiferencia para Octavio y se muestran convexas desde su punto de vista (es decir, vistas desde abajo a la izquierda). Las curvas naranjas se aplican a Abby y son convexas como se ve desde arriba a la derecha. Moverse hacia arriba y hacia la derecha aumenta la asignación de Octavio y lo coloca en una curva de indiferencia más deseable, mientras que a Abby la coloca en una menos deseable.
Las curvas de indiferencia convexas se consideran el caso habitual. Corresponden a rendimientos decrecientes de cada bien en relación con el otro.
El intercambio dentro del mercado comienza a partir de una asignación inicial conocida como dotación .
El uso principal del cuadro de Edgeworth es presentar temas de la teoría del equilibrio general en una forma en la que las propiedades puedan visualizarse gráficamente. También puede mostrar la dificultad de avanzar hacia un resultado eficiente en presencia de un monopolio bilateral . [1] En el último caso, sirve como precursor del problema de negociación de la teoría de juegos que permite una solución numérica única. [2] [3]
La caja de Edgeworth lleva el nombre de Francis Ysidro Edgeworth , [4] quien la presentó en su libro Mathematical Psychics: An Essay on the Application of Mathematics to the Moral Sciences , 1881. [5] La representación original de dos ejes de Edgeworth se desarrolló en la actual diagrama de caja familiar de Pareto en su Manual de Economía Política de 1906 y que fue popularizado en una exposición posterior de Bowley . La versión moderna del diagrama se conoce comúnmente como caja de Edgeworth-Bowley . [6]
El marco conceptual de equilibrio en una economía de mercado fue desarrollado por Léon Walras [7] y ampliado por Vilfredo Pareto . [8] Fue examinado con mucha atención a la generalidad y el rigor por economistas matemáticos del siglo XX, incluidos Abraham Wald , [9] Paul Samuelson , [10] Kenneth Arrow y Gérard Debreu . [11] Esto fue parte de un movimiento más amplio en el que Wald también buscó aportar mayor rigor a la teoría de la decisión y muchos matemáticos se concentraron en minimizar la dependencia del axioma de elección .
La teoría de los mercados walrasianos se ha esforzado por encontrar las premisas más generales a partir de las cuales se puede obtener una conclusión determinada. Las áreas en las que las premisas pueden fortalecerse o debilitarse incluyen:
También se hacen suposiciones de naturaleza más técnica, por ejemplo, no reversibilidad, saturación , etc.
La búsqueda del rigor no siempre conduce a la inteligibilidad. En este artículo las curvas de indiferencia se tratarán como primitivas. Al principio los consideraremos convexos y diferenciables y nos concentraremos en los equilibrios interiores, pero posteriormente relajaremos estos supuestos.

Como sólo hay dos mercancías, el precio efectivo es el tipo de cambio entre ellas. Nuestro objetivo es encontrar el precio al que se puede alcanzar el equilibrio del mercado, que será un punto en el que no se deseen más transacciones, a partir de una dotación determinada. Estas cantidades estarán determinadas por las curvas de indiferencia de los dos consumidores como se muestra en la Fig. 2.
Supondremos que todos los días Octavio y Abby van al mercado con dotaciones (ω x ,ω y ) y (Ω x – ω x , Ω y – ω y ) de los dos productos, correspondientes a la posición ω en el diagrama. Los dos consumidores intercambiarán entre sí bajo un comportamiento de mercado competitivo. Este supuesto requiere una cierta suspensión de la incredulidad, ya que las condiciones para la competencia perfecta –que incluyen un número infinito de consumidores– no se cumplen.
Si dos X se intercambian por una sola Y , entonces la transacción de Octavio y Abby los llevará a algún punto a lo largo de la línea gris sólida, que se conoce como línea presupuestaria . (Para ser más precisos, una línea presupuestaria puede definirse como una línea recta que pasa por el punto de dotación y representa asignaciones que se pueden obtener mediante intercambio a un precio determinado). Las líneas presupuestarias para un par de otros precios también se muestran como líneas discontinuas y punteadas en la figura 1. 2.
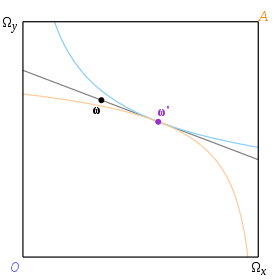
El equilibrio correspondiente a una determinada dotación ω está determinado por el par de curvas de indiferencia que tienen una tangente común tal que esta tangente pasa por ω . Usaremos el término "línea de precios" para denotar una tangente común a dos curvas de indiferencia. Por tanto, un equilibrio corresponde a una recta presupuestaria que también es una recta de precios, y el precio de equilibrio es la pendiente de la recta. En la Fig. 3 ω es la dotación y ω ' es la asignación de equilibrio.
El razonamiento detrás de esto es el siguiente.

En primer lugar, cualquier punto del cuadro debe estar exactamente en una de las curvas de indiferencia de Abby y exactamente en una de las de Octavio. Si las curvas se cruzan (como se muestra en la Fig. 4), entonces dividen el vecindario inmediato en cuatro regiones, una de las cuales (que se muestra en verde pálido) es preferible para ambos consumidores; por lo tanto, un punto en el que se cruzan las curvas de indiferencia no puede ser un equilibrio, y un equilibrio debe ser un punto de tangencia.
En segundo lugar, el único precio que puede mantenerse en el mercado en el punto de tangencia es el dado por la pendiente de la tangente, ya que sólo a este precio los consumidores estarán dispuestos a aceptar intercambios limitadamente pequeños.
Y en tercer lugar (el punto más difícil), todos los intercambios que lleven a los consumidores por el camino de ω al equilibrio deben realizarse al mismo precio. Si se acepta esto, entonces ese precio debe ser el operativo en el punto de tangencia, y el resultado sigue.
En una economía bipersonal no hay garantía de que todos los intercambios se realicen al mismo precio. Pero el propósito del cuadro de Edgeworth no es ilustrar la fijación de precios que puede tener lugar cuando no hay competencia, sino más bien ilustrar una economía competitiva en un caso mínimo. Así que podemos imaginar que en lugar de una sola Abby y un solo Octavio tenemos un número infinito de clones de cada uno, todos llegando al mercado con dotaciones idénticas en momentos diferentes y negociando gradualmente su camino hacia el equilibrio. Un Octavio recién llegado puede intercambiar a precio de mercado con una Abby que está cerca del equilibrio, y mientras una Abby recién llegada intercambie con un Octavio casi satisfecho, los números se equilibrarán. Para que el intercambio funcione en una economía grande y competitiva, debe reinar el mismo precio para todos. Por tanto, el intercambio debe mover la asignación a lo largo de la línea de precios tal como la hemos definido. [12]
En consecuencia, la tarea de encontrar un equilibrio competitivo se reduce a la tarea de encontrar un punto de tangencia entre dos curvas de indiferencia cuya tangente pasa por un punto dado. El uso de curvas de oferta (descritas a continuación) proporciona un procedimiento sistemático para hacerlo.
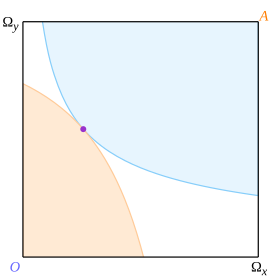
Se dice que una asignación de bienes "domina en el sentido de Pareto" a otra si es preferible para un consumidor y no peor para el otro. Se dice que una asignación es " óptima de Pareto " (o "eficiente de Pareto") si ninguna otra asignación de Pareto la domina. El conjunto de asignaciones óptimas de Pareto se conoce como conjunto de Pareto (o "lugar eficiente").
Considere un par de curvas tangenciales, una para cada consumidor, como se ilustra en la Fig. 5, donde el punto de tangencia se muestra con un punto violeta. Entonces, la convexidad garantiza que las curvas no pueden interceptarse más que en el punto de tangencia y, en consecuencia, la caja se divide en 3 regiones. El área azul pálido es preferible hasta el punto de tangencia para Octavio pero peor para Abby; la zona naranja pálida es preferible para Abby pero peor para Octavio; y la zona blanca es peor para ambos. Se aplican consideraciones similares a los límites. De ello se deduce que el punto de tangencia es óptimo de Pareto.

Por tanto, el conjunto de Pareto es el lugar geométrico de los puntos de tangencia de las curvas. Esta es una línea que conecta el origen de Octavio (O) con el de Abby (A). En la Fig. 6 se muestra un ejemplo, donde la línea violeta es el conjunto de Pareto correspondiente a las curvas de indiferencia para los dos consumidores.
El vocabulario utilizado para describir los diferentes objetos que forman parte de la caja de Edgeworth diverge. El conjunto completo de Pareto a veces se denomina curva de contrato , mientras que Mas-Colell et al. restrinja la definición de la curva de contrato sólo a aquellos puntos del conjunto de Pareto que hacen que tanto Abby como Octavio estén al menos tan bien como en su dotación inicial. Otros autores que tienen una inclinación más teórica de juegos , como Martin Osborne y Ariel Rubinstein , [13] utilizan el término núcleo para la sección del conjunto de Pareto que es al menos tan buena para cada consumidor como la dotación inicial.
Dado que el conjunto de Pareto es el conjunto de puntos donde las curvas de indiferencia de los consumidores son tangenciales, también es el conjunto de puntos donde la tasa marginal de sustitución de cada consumidor es igual a la de la otra persona. [14]
Hemos visto que los puntos de tangencia de las curvas de indiferencia son los óptimos de Pareto, pero también vimos anteriormente que los equilibrios económicos son aquellos puntos en los que las curvas de indiferencia son tangenciales a una línea de precios común. De ello se deduce que los equilibrios son precisamente los óptimos de Pareto.
Este argumento se aplica con una restricción incluso si las curvas son indiferenciables o si el equilibrio está en la frontera. La condición para el equilibrio es que no se produzca más intercambio, y la condición para que no se produzca más intercambio es que no haya una dirección de movimiento que beneficie a un consumidor sin perjudicar al otro; y esto es equivalente a la definición de un óptimo de Pareto. [15]
La restricción es que el equilibrio implica que no se puede realizar ninguna mejora local ; en otras palabras, que el punto es "localmente" óptimo de Pareto. Pero hoy en día el óptimo de Pareto se considera global por definición. [16] Por lo tanto, si la naturaleza de las curvas de indiferencia permite que surjan óptimos no globales (lo que no puede suceder si son convexas), entonces es posible que los equilibrios no sean óptimos de Pareto.
La competencia perfecta no es una condición previa para el teorema. Mientras los consumidores sean libres de intercambiar, y continuarán haciéndolo hasta que no exista un intercambio mutuamente aceptable, se alcanzará el equilibrio y será (al menos "localmente") óptimo de Pareto. [17]

Consideremos ahora una economía en la que los consumidores tienen dotaciones ω como se muestra en la figura 7. Si se deja a su suerte, un mercado libre los llevará a ω' . Pero supongamos que alguna otra posición en el cuadro – digamos α' – se considera socialmente preferible. Podemos suponer que la posición socialmente deseada es óptima de Pareto.
Podemos pensar que las líneas de precios (que aparecen discontinuas en el diagrama) corresponden a diferentes distribuciones del ingreso real, y que el movimiento a lo largo de ellas es una reasignación de recursos mientras los ingresos permanecen fijos.
Entonces, para reposicionar la sociedad en el punto deseado α' no es necesario que el gobierno redistribuya los recursos de tal manera que Octavio tenga (α' x ,α' y ) y Abby tenga el complemento: basta con reasignar los recursos. llevar la economía a cualquier punto (digamos α ) en la línea de precios que pasa por α' , y luego dejar que el mercado encuentre su propio equilibrio. De hecho, mientras el gobierno reconozca una distribución deseable del ingreso, no necesita tener idea alguna de la asignación óptima de los recursos.
En una formulación para una economía más general, se entendería que el teorema dice que α' puede alcanzarse mediante una transferencia monetaria seguida del libre juego del intercambio de mercado; pero falta dinero en la caja de Edgeworth.
El segundo teorema fundamental no proporciona un plan para corregir los males de la sociedad. El gobierno puede decidir reasignar recursos entre Octavio y Abby, moviéndolos de ω a α antes de la negociación del día; y, en consecuencia, quien pierda puede decidir llevar menos al mercado al día siguiente. El segundo teorema fundamental no tiene en cuenta las distorsiones introducidas por la reasignación. [18]
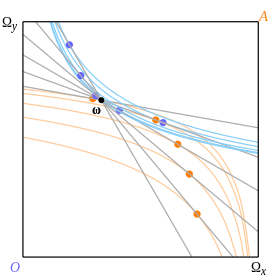
Las curvas de oferta proporcionan un medio para encontrar puntos de equilibrio y también son útiles para investigar su existencia y unicidad.
En el cuadro se pueden dibujar dos de estas curvas, una para cada consumidor y ambas dependiendo de la dotación. Giramos la línea presupuestaria alrededor de ω y trazamos los puntos más favorecidos de los dos consumidores a lo largo de la línea, como lo muestran los puntos coloreados en la Fig. 8. Estos son puntos en los que la línea es tangencial a sus propias curvas de indiferencia.

El lugar geométrico de los puntos más favorecidos de un consumidor es su curva de oferta. La figura 9 muestra la curva de oferta de Octavio en azul oscuro y la de Abby en marrón. Se encuentran en el punto ω ' y la recta presupuestaria de equilibrio (dibujada en gris) es la que pasa por este punto. Las curvas de indiferencia que pasan por ω ' para los dos consumidores se muestran en colores más pálidos.
Una curva de oferta pasa necesariamente por el punto de dotación ω . Si tomamos a Abby como ejemplo, observamos que una de sus curvas de indiferencia debe pasar por ω y que se puede elegir una recta presupuestaria que tenga el mismo gradiente que la curva de indiferencia aquí, lo que convierte a ω en el punto más favorecido para esta recta.
En consecuencia, las curvas de oferta de los dos consumidores necesariamente se cruzan en ω ; pero la propiedad que hace que esto suceda es que ω es el único punto de intersección posible consistente con líneas presupuestarias de diferente gradiente y que, por lo tanto, no constituye necesariamente un equilibrio.
Cualquier intersección de curvas de oferta en un punto distinto de ω determina un equilibrio estable. Si las dos curvas de oferta son tangenciales en el punto de dotación, entonces este punto es efectivamente un equilibrio y su tangente común es la recta presupuestaria correspondiente. [19]
Las curvas de oferta fueron utilizadas por primera vez por Vilfredo Pareto ; consulte su Manuale / Manuel Chap. III, §97. Las llamó "curvas de cambio" ( linee dei baratti / lignes des échanges ), y el nombre que dio a la asignación preferida de Octavio a lo largo de una línea presupuestaria fue su "punto de equilibrio".
Esta asignación preferida a veces se conoce hoy en día como la "demanda" de Octavio, que constituye una descripción asimétrica de un hecho simétrico. Una asignación determina tanto la participación de Abby como la de Octavio y, por lo tanto, es tanto una oferta como una demanda.
Offre significa "oferta" en francés, por lo que llamar a una curva de oferta un locus de demandas equivale a llamar a una curva de oferta un locus de demandas.
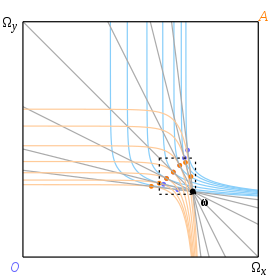

A partir de consideraciones económicas, podría suponerse que si existe una tangente compartida a través de una dotación dada, y si las curvas de indiferencia no tienen una forma patológica, entonces el punto de tangencia será único. Esto resulta no ser cierto. Las condiciones para la unicidad del equilibrio han sido objeto de extensas investigaciones: véase Teoría del equilibrio general .
Higos. 9 y 10 ilustran un ejemplo de Mas-Colell et al. en el que tres equilibrios distintos corresponden al punto de dotación ω . Las curvas de indiferencia son:
(Octavio)
(Abby).
Las curvas de indiferencia llenan el cuadro pero solo se muestran cuando son tangenciales a algunas líneas presupuestarias representativas. Las curvas de oferta, dibujadas en la Fig. 11, se cruzan en tres puntos mostrados con grandes puntos grises y correspondientes a tipos de cambio de 1 ⁄ 2 , 1 y 2.
Los primeros exámenes de las propiedades del equilibrio se basaron en una definición implícita de tangencia, y parece que se asumió implícitamente la convexidad. [20] No había duda de que se alcanzaría el equilibrio: el ascenso del gradiente conduciría a él. Pero los resultados carecieron de generalidad.

Kenneth Arrow y Gérard Debreu publicaron artículos de forma independiente en 1951 llamando la atención sobre las limitaciones en las pruebas de cálculo de los teoremas de equilibrio. [21] Arrow mencionó específicamente la dificultad causada por los equilibrios en la frontera, y Debreu el problema de las curvas de indiferencia no diferenciables.
Sin pretender una cobertura exhaustiva, es fácil ver en términos intuitivos cómo ampliar nuestros métodos para aplicarlos a estos casos. Necesitamos ampliar el concepto de tangente para incluir cualquier línea que toque la curva: una tangente en el sentido etimológico más que en el del cálculo diferencial. En el ejemplo de la figura 12 hay un arco de líneas de precios legales que pasa por un punto de contacto, cada una de las cuales toca curvas de indiferencia sin cortarlas dentro de la caja y, en consecuencia, hay un rango de equilibrios posibles para una dotación dada.
Los equilibrios de la figura 12 no son puntos en los que las curvas sean verdaderas tangentes entre sí. Sin embargo, tienen una propiedad que generaliza la definición en términos de tangentes, y es que las dos curvas pueden estar separadas localmente por una línea recta.
Arrow y Debreu definieron el equilibrio de la misma manera en sus artículos (independientes) de 1951 sin proporcionar ninguna fuente o justificación para su definición. Mantuvieron su definición en su artículo conjunto (sobre la existencia del equilibrio) de 1954. [22] La nueva definición requería un cambio de técnica matemática del cálculo diferencial a la teoría de conjuntos convexos .
En efecto, su definición era la siguiente: un equilibrio alcanzable a partir de una dotación ω consiste en una asignación x y una línea presupuestaria que pasa por x y ω tal que no hay ningún punto a lo largo de la línea en el que cualquiera de los consumidores prefiera (estrictamente) x . Un par que comprende una asignación y una línea que satisface esta propiedad se conoce como equilibrio "walrasiano" o " competitivo" .
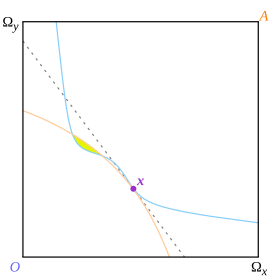
La línea presupuestaria de esta definición es una línea que separa las curvas de indiferencia de los dos consumidores, pero lo hace a nivel global y no local. Arrow y Debreu no explican por qué requieren una separación global, lo que puede haber facilitado sus pruebas, pero se puede considerar que tiene consecuencias inesperadas. En la figura 13, el punto x es un punto de tangencia que también es un punto en el que las curvas de indiferencia están localmente separadas por la línea discontinua de precios; pero como no están globalmente separados, el punto no es un equilibrio según la definición de Arrow y Debreu.

En la Fig. 14, el punto x es un óptimo de Pareto que no satisface la definición de equilibrio competitivo. La cuestión de si la economía se estabilizaría en ese punto es bastante independiente de si satisface una definición dada de equilibrio; evidentemente en este caso efectivamente se asentaría allí.
Arrow y Debreu siempre incluyeron la convexidad de las curvas de indiferencia entre sus "supuestos". El término "supuestos" es vago y podría referirse a una presuposición que subyace tanto a definiciones como a teoremas, o a una premisa que sólo es necesaria para estos últimos. Dado que su definición no incluye todos los equilibrios que pueden existir cuando las curvas pueden ser no convexas, es posible que se refirieran al supuesto de convexidad en el primer sentido. Sea o no así, la definición ha sido ampliamente adoptada sin ninguna restricción de dominio.
A veces se ha descubierto que se pueden derivar resultados según su definición sin asumir convexidad en la demostración (el primer teorema fundamental de la economía del bienestar es un ejemplo).
En algunas economías no habrá un punto de descanso alcanzable a partir de una determinada dotación mediante el intercambio a precios uniformes; por tanto, no existe ningún punto de descanso que satisfaga la definición de equilibrio competitivo. Las familias de curvas del patrón de la Fig. 14 son un ejemplo de esto.
Al definir el equilibrio como "equilibrio competitivo", el primer teorema fundamental puede demostrarse incluso si las curvas de indiferencia no necesitan ser convexas: cualquier equilibrio competitivo es (globalmente) óptimo de Pareto. Sin embargo, la prueba ya no es obvia y se remite al lector al artículo sobre Teoremas fundamentales de la economía del bienestar .
No se habría considerado que se cumpliera el mismo resultado (con curvas de indiferencia no convexas) bajo la definición de tangencia de equilibrio. El punto x de la Fig. 13 se habría considerado un equilibrio que no era (globalmente) óptimo ya que la región amarilla de Pareto lo domina.
De ello no se sigue que el resultado se haya fortalecido desde que la posibilidad de alcanzar el equilibrio se haya vuelto dudosa. En la figura 13, el punto x puede no ser un "equilibrio competitivo", pero la economía puede quedarse estancada allí impidiendo que alcance el equilibrio "verdadero" (y óptimo de Pareto) en la región amarilla.
Siempre se consideró esencial para el primer teorema del bienestar que realmente se alcanzaría el equilibrio. La interpretación de Lerner del teorema fue que "Afortunadamente, la asignación óptima de bienes se puede alcanzar automáticamente". [23] Sin embargo, nada puede garantizar que se alcanzará un óptimo global cuando estén presentes óptimos locales. Si el concepto de equilibrio incluye óptimos locales como x , entonces el equilibrio puede ser alcanzable pero subóptimo; Si se excluyen esos puntos, entonces el equilibrio puede ser óptimo pero inalcanzable.
Las diferencias causadas por la no convexidad se arraigan más profundamente cuando analizamos el segundo teorema fundamental. No todo óptimo de Pareto es un equilibrio competitivo (aunque aún puede ser un lugar de descanso para la economía). En consecuencia, es necesario dar al teorema la convexidad de las preferencias como premisa, o bien formularlo de tal manera que el "equilibrio" no se entienda como el "equilibrio competitivo" tal como se definió anteriormente.