El teorema fue publicado por primera vez por J. Howard Redfield en 1927.Sea X un conjunto finito y sea G un grupo de permutaciones de X (o un grupo de simetría finito que actúa sobre X).En la versión más general e importante del teorema, los colores también se ponderan de una o más maneras, y podría haber un número infinito de colores siempre que el conjunto de colores tenga una función generadora con coeficientes finitos.En el caso univariado, supongamos que es la función generadora del conjunto de colores, de modo que existen f w colores de peso w para cada entero w ≥ 0.El teorema establece que la función generadora F del número de disposiciones de colores en peso viene dada por: o en el caso multivariado: Para reducir a la versión simplificada proporcionada anteriormente, si hay m colores y todos tienen peso 0, entonces f (t) = m y En la célebre aplicación de contar árboles (ver más abajo) y moléculas acíclicas, una disposición de "cuentas de colores" es en realidad una disposición de disposiciones, como las ramas de un árbol enraizado.Así, la función generadora f para los colores se deriva de la función generadora F para las disposiciones, y el teorema de enumeración de Pólya se convierte en una fórmula recursiva.¿Cuántas formas hay de colorear los lados de un cubo tridimensional con m colores, hasta la rotación del cubo?El grupo de rotación C del cubo actúa sobre los seis lados del cubo, que equivalen a cuentas.aristas posibles, mientras que el conjunto de colores Y = {negro, blanco} corresponde a aristas que están presentes (negro) o ausentes (blanco).Para este último propósito, podemos decir que un borde negro o presente tiene peso 1, mientras que un borde ausente o blanco tiene peso 0.es la función generadora del conjunto de colores.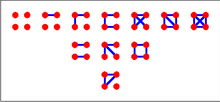Así, según el teorema de enumeración, la función generadora de gráficos en 3 vértices hasta el isomorfismo es lo que simplifica a Por lo tanto, hay un gráfico cada uno con 0 a 3 aristas.El índice de ciclo del grupo S 4 que actúa sobre el conjunto de 6 aristas es (ver aquí) Por lo tanto lo que simplifica a Estos gráficos se muestran a la derecha.El conjunto T3 de árboles ternarios enraizados consta de árboles enraizados donde cada nodo (o vértice que no es hoja) tiene exactamente tres hijos (hojas o subárboles).A la derecha se muestran pequeños árboles ternarios.Tenga en cuenta que los árboles ternarios enraizados con n nodos son equivalentes a árboles enraizados con n vértices de grado como máximo 3 (ignorando las hojas).En general, dos árboles enraizados son isomorfos cuando uno puede obtenerse del otro permutando los hijos de sus nodos.Definimos el peso de dicho árbol ternario como el número de nodos (o vértices que no son hojas).Se puede ver un árbol ternario enraizado como un objeto recursivo que es una hoja o un nodo con tres hijos que son a su vez árboles ternarios enraizados.que por el teorema de enumeración da como función generadora para árboles ternarios enraizados, ponderada por uno menos que el número de nodo (ya que la suma de los pesos secundarios no tiene en cuenta la raíz), de modo que Esto equivale a la siguiente fórmula de recurrencia para el número tn de árboles ternarios enraizados con n nodos: donde a, b y c son números enteros no negativos.fijado por la permutación g de G sobre todas las permutaciones g. La versión ponderada del teorema tiene esencialmente la misma prueba, pero con una forma refinada del lema de Burnside para enumeración ponderada.denota el término monomio correspondiente de f .que también están fijados por g. Si luego sumamos todos los pesos posibles, obtenemos Mientras tanto, un elemento de grupo g con estructura de ciclosí y solo si la función φ es constante en cada ciclo q de g. Para cada ciclo q, la función generadora en peso de | q | colores idénticos del conjunto enumerado por f es De ello se deduce que la función generadora en peso de los puntos fijados por g es el producto del término anterior sobre todos los ciclos de g, es decir Sustituyendo esto en la suma de todos los g se obtiene el índice de ciclo sustituido como se afirma.
Todos los gráficos en tres vértices.
Gráficos no isomorfos en tres vértices.
Clases de isomorfismo de gráficos en cuatro vértices.
Archivo:TernaryTrees.png
Árboles ternarios enraizados en 0, 1, 2, 3 y 4 nodos (=vértices sin hojas). La raíz se muestra en azul, las hojas no. Cada nodo tiene tantas hojas como para que el número de hijos sea igual a 3.
