Relación binaria

Una relación binaria R es el subconjunto de los elementos del producto cartesianoEn primer lugar diferenciamos las relaciones binarias homogéneas, de las heterogéneas.Una relación homogénea puede ser tratada como heterogénea con los mismos subtipos, pero no al contrario.Una relación binaria R es homogénea si los conjuntos son iguales: Dado que, la relación binaria R queda determinada como: Una forma de representar el producto cartesiano es: Tomando como conjunto inicial y final a, se asocia un elemento inicial a uno final dentro de un mismo conjunto, determinando una operación matemática, teniendo siempre en cuenta que si bien el conjunto inicial y final son el mismo, la relación es unidireccional.Dado un conjunto A, formado por los siguientes elementos: Y una relación R entre los elementos del conjunto, definida así: Podemos ver que los pares ordenados que tienen sus dos términos iguales pertenecen a la relación: Luego la relación R es reflexiva.La relación R, también se puede representar en coordenadas cartesianas la función identidad.En el eje horizontal (abscisas) representamos el conjunto inicial, de izquierda a derecha, y en el eje vertical(ordenadas) el conjunto final, de abajo arriba, si un determinado par pertenece a la relación se coloca una cruz en la casilla correspondiente, si no pertenece se deja en blanco, representando de este modo en coordenadas cartesianas la relación binaria.En la diagonal principal, inferior izquierda, superior derecha, corresponde a los pares ordenados en los que sus dos elementos son iguales, si todas las casillas de esta diagonal tienen aspas, la relación es reflexiva.Como puede verse en el diagrama, la relación estudiada es reflexiva, dado que: Para todo elemento e del conjunto A, el par ordenado (e,e) pertenece a la relación R. En cualquiera de las tres formas de representación vistas: enumeración de pares ordenados, donde los pares (e,e) pertenecen a la relación, el diagrama sagital, con una flecha que sale y llega a cada elemento del conjunto, o en coordenadas cartesianas, donde hay cruces en la diagonal principal, en todos los casos se representa una relación reflexiva, en la que todo elemento del conjunto está relacionado consigo mismo.Ver diagrama: Las relaciones irreflexivas son un caso particular de las no reflexivas.Dado el conjunto: y la relación entre los elementos de este conjunto: Podemos ver que: Para todo elemento e del conjunto A, el par ordenado (e,e) no pertenece a la relación R, luego esta relación en irreflexiva.La representación de la relación en coordenadas cartesianas nos permite ver que la diagonal principal no tiene ninguna cruz, lo que es equivalente a la irrefrexibilidad de la relación.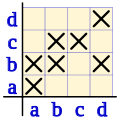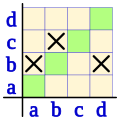Si representamos la relación binaria en coordenadas cartesianas, podemos ver que en la diagonal principal no todas las casillas tienen un aspa, luego la relación no es reflexiva, y tampoco están todas en blanco luego tampoco es irreflexiva, esto es un relación binaria no reflexiva y no irreflexiva, al darse estas dos condiciones simultáneamente en una misma relación.Así por ejemplo si consideramos el conjunto de los números naturales, y definimos la distancia D entre dos números, como el valor absoluto de su diferencia: y decimos que dos números naturales a, b están próximos si su distancia es a lo sumo un valor D conocido, tenemos que la relación binaria de proximidad es: es una relación de dependencia, dado que es reflexiva: es simétrica: relación binaria de proximidad no es transitiva, dado que: que la distancia entre a y b sea a lo sumo D y que la distancia entre b y c no supere D, no implica necesariamente que la distancia entre a y c no sea mayor que D. Esta relación de dependencia entre los números por su distancia no es una clase de equivalencia, pero si denota una dependencia entre ellos.Una relación binaria define un conjunto preordenado si es reflexiva y transitiva:En Aritmética modular se define la operación módulo como el resto de la división, así: se dice que dos números son congruentes módulo n, si al dividir cada uno de esos números por n dan el mismo resto: el 8 y el 17 son congruentes módulo 3 dado que al dividirlos por 3 en los dos casos dan por resto 2.La congruencia modular de grado n, de los números naturales, es una Relación de equivalencia, dado que es reflexiva: es simétrica: y es transitiva Un conjunto A se dice que esta parcialmente ordenado respecto a una relación binaria R si la relación R es reflexiva, transitiva y antisimétrica: Dado un conjunto A, y una relación binaria R entre sus elementos:Se dice que R define un conjunto parcialmente ordenado, si cumple: 1.- La propiedad reflexiva: Todo elemento a de A está relacionado consigo mismo.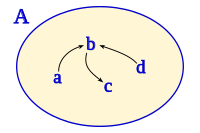Esta relación no es total dado que: Que se denominan no comparables, los pares de conjuntos no comparables son: A la vista del diagrama, los conjuntos que se pueden alcanzar siguiendo el sentido de las flechas se denominan comparables y determinan la estructura del orden parcial.Si tomamos el conjunto de los números enteros Z, por ejemplo, respecto a la relación binaria entre sus elementos menor o igual, podemos ver que es reflexiva: es transitiva: es antisimetrica: y es total: Dado un conjunto A y una relación binariacumple las propiedades: Dado un conjunto A en el que se ha definido una relación binariaEl elemento y de A que cumple: Se denomina máximo y define una cota superior en A; el elemento máximo es único.Del mismo modo el elemento z de A que cumple: Se denomina mínimo y define una cota inferior en A; el elemento mínimo es único.Una relación binaria entre dos conjuntos A y B, se llama heterogénea cuando A es distinto de B: Lo que también se llama correspondencia matemática.[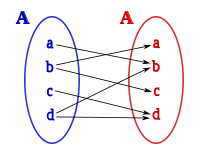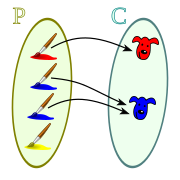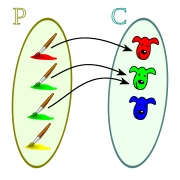2]​[3]​ A la derecha podemos ver lo que se denomina un diagrama sagital, en el cual se representan los dos conjuntos de la relación binaria, asociando los elementos de uno y otro conjunto con una flecha, que sale del elemento origen y llega al elemento imagen, en el diagrama pueden verse un conjunto de pinceles con pintura de color y un conjunto de caras pintadas, asociando a cada pincel la cara que está pintada del mismo color.En el diagrama podemos ver el conjunto inicial ( o dominio ) de pinceles P, sobre el que está definida la relación: Solo algunos elementos del conjunto inicial tienen asociado un elemento, estos elementos forman el conjunto origen: Y el conjunto final ( o codominio ) de caras pintadas C es: Los elementos del conjunto final a los que se les ha asociado un origen se llama conjunto imagen: La relación binaria es la formada por los pares ordenados: Una relación binaria homogénea: Puede ser tratada como heterogénea considerando el conjunto inicial y final como distintos, si lo que se está tratando es una correspondencia, con la misma validez que si los conjuntos serían distintos, pudiendo realizar simultáneamente su análisis como relación homogénea, si es factible.Partiendo de una relación binarias heterogénea R, entre los conjunto A y B: Por su importancia podemos distinguir las siguientes condiciones, que nos permiten diferenciar los subtipos de correspondencias.