Problema de la secretaria

y L. Gerald Marnie, quienes de forma independiente habían ideado un problema equivalente en 1958; Lo llamaron "game of googol".

Fox y Marnie no conocían la solución óptima; Gardner pidió consejo a Leo Moser, quien (junto con J. R. Pounder) proporcionó un análisis correcto para su publicación en la revista.

Poco después, varios matemáticos escribieron a Gardner para contarle sobre el problema equivalente que habían escuchado a través de los rumores, todo lo cual probablemente se remonta al trabajo original de Flood.

[13]​ La ley 1/e de mejor elección se debe a F. Thomas Bruss.

[14]​ Ferguson tiene una extensa bibliografía y señala que un problema similar (pero diferente) había sido considerado por Arthur Cayley en 1875 e incluso por Johannes Kepler mucho antes, quien pasó dos años investigando a 11 candidatos al matrimonio durante 1611-1613 después de la muerte de su primera esposa.

Después de cada entrevista, hay que decidir si la contratamos o no.

John Gilbert y Frederick Mosteller, de la Universidad de Harvard, demostraron que es posible aumentar la probabilidad entrevistando a 37 personas y luego parando en la siguiente mejor que las 37 entrevistadas.

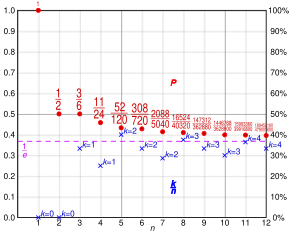
Fijamos pues un número k y calculemos ahora la probabilidad de ganar.

k implica que la entrevista a la mejor pasó ya y fue rechazada.