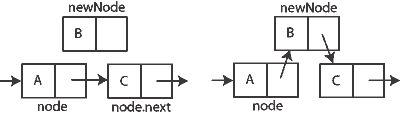
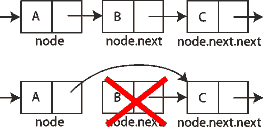
Lista enlazada
Las listas enlazadas permiten inserciones y eliminación de nodos en cualquier punto de la lista en tiempo constante (suponiendo que dicho punto está previamente identificado o localizado), pero no permiten un acceso aleatorio.
Lenguajes tales como Lisp, Scheme y Haskell tienen estructuras de datos ya construidas, junto con operaciones para acceder a las listas enlazadas.
Lenguajes imperativos u orientados a objetos tales como C o C++ y Java, respectivamente, disponen de referencias para crear listas enlazadas.
Bert Green, del Lincoln Laboratory del MIT, publicó un estudio titulado Computer languages for symbol manipulation en IRE Transaction on Human Factors in Electronics en marzo de 1961 que resumía las ventajas de las listas enlazadas.
Una variante desarrollada por TSC se comercializó a Smoke Signal Broadcasting en California, usando listas doblemente enlazadas del mismo modo.
En algún lenguaje de muy bajo nivel, XOR-Linking ofrece una vía para implementar listas doblemente enlazadas, usando una sola palabra para ambos enlaces, aunque esta técnica no se suele utilizar.
Como en una lista enlazada simple, los nuevos nodos pueden ser solo eficientemente insertados después de uno que ya tengamos referenciado.
Como en una lista doblemente enlazada, las inserciones y eliminaciones pueden ser hechas desde cualquier punto con acceso a algún nodo cercano.
Aunque estructuralmente una lista circular doblemente enlazada no tiene ni principio ni fin, un puntero de acceso externo puede establecer el nodo apuntado que está en la cabeza o al nodo cola, y así mantener el orden tan bien como en una lista doblemente enlazada.
Como muchas opciones en programación y desarrollo, no existe un único método correcto para resolver un problema.
Este ejemplo muestra las fuerzas y debilidades de las listas enlazadas frente a los vectores, ya que viendo a la gente como nodos conectados entre sí en una lista circular se observa como es más fácil suprimir estos nodos.
También permiten el acceso rápido al primer y último elemento por medio de un puntero simple.
El Nodo Centinela es definido como otro nodo en una lista doblemente enlazada, la asignación del puntero frente no es necesaria y los puntero anterior y siguiente estarán apuntando a sí mismo en ese momento.
Si los punteros anterior y siguiente apuntan al Nodo Centinela la lista se considera vacía.
Entonces una lista enlazada puede ser construida, creado un vector con esta estructura, y una variable entera para almacenar el índice del primer elemento.
Muchos lenguajes de programación tales como Lisp y Scheme tienen listas enlazadas simples ya construidas.
Aunque las celdas cons pueden ser usadas para construir otras estructuras de datos, este es su principal objetivo.
En otros lenguajes, las listas enlazadas son típicamente construidas usando referencias junto con el tipo de dato récord.
El almacenamiento externo, por otro lado, tiene la ventaja de ser más genérico, en la misma estructura de datos y código máquina puede ser usado para una lista enlazada, no importa cual sea su tamaño o los datos.
Esto hace que sea más fácil colocar el mismo dato en múltiples listas enlazadas.
Aunque con el almacenamiento interno los mismos datos pueden ser colocados en múltiples listas incluyendo múltiples referencias siguientes en la estructura de datos del nodo, esto podría ser entonces necesario para crear rutinas separadas para añadir o borrar celdas basadas en cada campo.
Otro enfoque que puede ser usado con algunos lenguajes implica tener diferentes estructuras de datos, pero todas tienen los campos iniciales, incluyendo la siguiente (y anterior si es una lista doblemente enlazada) referencia en la misma localización.
Buscando un elemento específico en una lista enlazada, incluso si esta es ordenada, normalmente requieren tiempo O (n) (búsqueda lineal).
Otro enfoque común es indizar una lista enlazada usando una estructura de datos externa más eficiente.
Por ejemplo, podemos construir un árbol rojo-negro o una tabla hash cuyos elementos están referenciados por los nodos de las listas enlazadas.
Esto hace que los algoritmos de insertar y borrar nodos en las listas sean algo especiales.
Advertimos que BorrarPrincipio pone PrimerNodo a nulo cuando se borra el último elemento de la lista.
Una función simétrica que inserta al final: Borrar un nodo es fácil, solo requiere usar con cuidado firstNode y lastNode.
Una consecuencia especial de este procedimiento es que borrando el último elemento de una lista se ponen PrimerNodo y UltimoNodo a nulo, habiendo entonces un problema en una lista que tenga un único elemento.
Esto nos permite normalmente evitar el uso de PrimerNodo y UltimoNodo, aunque si la lista estuviera vacía necesitaríamos un caso especial, como una variable UltimoNodo que apunte a algún nodo en la lista o nulo si está vacía.