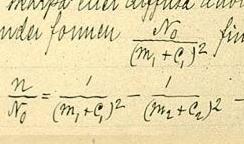Encontrando que las curvas resultantes tenían formas similares, buscó una sola función capaz de generar todas esas curvas, cuando fuera usada la constante apropiada.cuando vio la fórmula de Balmer para el espectro del hidrógeno λ=hm ²/(m ² − 4).Rydberg reescribió esto en términos del número de ondas como n = no − 4no/m ².Esto mostró que el hidrógeno era un caso especial con m= 0 y C0=4no.En la concepción del átomo de Bohr, los números enteros de Rydberg (y Balmer) n representan las órbitas a diferentes distancias enteras del átomo.Una frecuencia (o energía espectral) emitida en una transición desde n1 a n2 por lo tanto, representa la energía del fotón emitido o absorbido cuando un electrón hace un salto desde el orbital 1 hasta el orbital 2.funcione a partir del 2 al infinito, las líneas espectrales conocidas como las series de Lyman convergen a 91 nm son obtenidas, de la misma manera:La serie de Lyman está en el espectro ultravioleta mientras que la serie de Balmer está en el espectro visible y la serie de Paschen, Brackett, Pfund y Humphrey están en el espectro infrarrojo.La fórmula de arriba puede ser extendida para el uso con cualquier elemento químico similar al hidrógeno.donde Es importante notar que esta fórmula solo puede ser usada para átomos similares al hidrógeno, también llamados átomos hidrogénicos o hidrogenoides de elementos químicos, es decir con solo un electrón siendo afectado por carga nuclear efectiva.Ejemplos incluirían He+, Li2+, Be3+ etc., donde ningún otro electrón existe en el átomo.La fórmula de Rydberg proporciona las longitudes de onda correctas para los electrones extremadamente distantes, donde la carga nuclear efectiva puede ser estimada al igual que la del hidrógeno, puesto que todos sino una de las cargas nucleares han sido pantalleada por otros electrones, y la base del átomo tiene una carga positiva de +1.
La fórmula de Rydberg como aparecía en un escrito de noviembre de 1888
