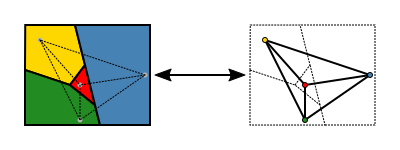
Teorema de los cuatro colores
Asumiendo que las regiones adyacentes comparten no solo un punto, sino todo un segmento de borde (frontera) en común.
Fue resuelto, a mediados de 1970, por Kenneth Appel y Wolfgang Haken.
Esto fue mejorado en 1997 por Robertson, Sanders, Seymour y Thomas, que consiguieron reducir el número de tales configuraciones a 633, lo que sigue siendo un caso de análisis extremadamente largo.
En primer lugar, todas las esquinas y puntos en común que pertenecen a tres o más países deben ser ignoradas.
Sin esta restricción, los mapas extraños (utilizando las regiones del área finita pero perímetro infinito) pueden requerir más de cuatro colores.
En segundo lugar, para el propósito del teorema cada "país" tiene que ser una región simplemente conexa o continua.
Debido a que el territorio de un país en particular debe ser del mismo color, si se permitiesen "países" no continuos, cuatro colores podrían no ser suficientes.
Una versión más simple del teorema utiliza la teoría de grafos.
En 1879 Alfred Bray Kempe anunció en la revista Nature que tenía una demostración para la conjetura.
Heawood no pudo demostrar que la conjetura no era válida, pero siguió trabajando en el coloreo de mapas, pudiendo probar que con cinco colores se podía colorear cualquier mapa.
Sin embargo, la demostración no es aceptada por todos los matemáticos dado que sería impracticable por su gran cantidad de detalles, de manera que una persona se vería imposibilitada para verificarlo manualmente.
En 1996, Neil Robertson, Daniel P. Sanders, Paul Seymour y Robin Thomas crearon un algoritmo de tiempo cuadrático (que requiere sólo
[9] El siguiente resumen está basado en el libro Every Planar Map is Four Colorable de Appel y Haken publicado en 1989.
En primer lugar, si el grafo tiene regiones o caras planas no triangulares, es decir, no tienen tres aristas como fronteras, se pueden agregar aristas al grafo (sin introducir nuevos vértices) de manera que cada región del grafo sea triangular, incluida la región exterior.
Llamemos a este grafo G. El grafo G no puede tener un vértice de grado 3 o menos, porque si g(v) ≤ 3, podemos eliminar v de G, y colorear con cuatro colores el grafo modificado más pequeño, y a continuación, añadir de nuevo el vértice v y colorearlo con un color diferente al de sus vecinos.
Kempe también demostró que G no puede tener ningún vértice de grado 4.
Se ha estudiado también el problema de colorear otras superficies que no sean equivalentes a un plano.
Alternativamente, para una superficie orientable, la fórmula puede ser dada en términos del género de la superficie, g: Esta fórmula, conocida como conjetura de Heawood, fue conjeturada por P. J. Heawood en 1890 y demostrada para los casos de superficies orientables (y no orientables) no acotadas por Gerhard Ringel y J. T. W. Youngs en 1968.
El conjunto luego requerirá n colores, o n+1 si se considera que el espacio vacío también toca cada varilla.
Para el número n puede tomarse un entero tan grande como se quiera.
Si ésta fuera la restricción, los grafos planos requerirían un número arbitrariamente grande de colores.
Otras falsas refutaciones violan los supuestos del teorema, como el uso de una región que consiste en múltiples partes desconectadas, o no permitir que las regiones del mismo color se toquen en un punto.