En física, geometría y análisis matemático, un objeto o ente es tridimensional si tiene tres dimensiones.El espacio a nuestro alrededor es tridimensional a simple vista, pero en realidad hay más dimensiones, por lo que también puede ser considerado un espacio tetra-dimensional si incluimos el tiempo como cuarta dimensión.[1] Sirve como modelo del universo físico (cuando no se considera la teoría de la relatividad), en el que existe toda la materia conocida.En este ejemplo clásico, cuando los tres valores se refieren a mediciones en diferentes direcciones (coordenadas), se pueden elegir tres direcciones cualquieras, siempre que los vectores en estas direcciones no se encuentren todos en el mismo espacio bidimensional (plano).El Libro XIII describe la construcción de los cinco sólidos platónicos regulares en una esfera.En el siglo XVII, el espacio tridimensional fue descrito con coordenadas cartesianas, con el advenimiento de la geometría analítica desarrollada por René Descartes en su obra La Géométrie y Pierre de Fermat en el manuscrito Ad locos planos et solidos isagoge (Introducción a los lugares geométricos planos y sólidos), inédito en vida de Fermat.Sin embargo, solo el trabajo de Fermat se ocupó del espacio tridimensional.En un espacio euclídeo convencional un objeto físico finito está contenido dentro de un ortoedro mínimo, cuyas dimensiones se llaman ancho, largo y profundidad o altura.Sin embargo, cuando se consideran fenómenos físicos como la gravedad, la teoría de la relatividad nos lleva a que el universo es un ente tetra-dimensional que incluye tanto dimensiones espaciales como el tiempo como otra dimensión.Diferentes observadores percibirán diferentes "secciones espaciales" de este espacio-tiempo por lo que el espacio físico es algo más complejo que un espacio euclídeo tridimensional.En las teorías recientes no existe una razón clara para que el número de dimensiones espaciales sean tres.Aunque existen ciertas intuiciones sobre ello: Ehrenfest señaló que en cuatro o más dimensiones las órbitas planetarias cerradas, por ejemplo, no serían estables (y por ende, parece difícil que en un universo así existiera vida inteligente preguntándose por la tridimensionalidad espacial del universo).Donde: Si la geometría del espacio d-dimensional no es euclídea entonces la expresión anterior debe corregirse según la curvatura.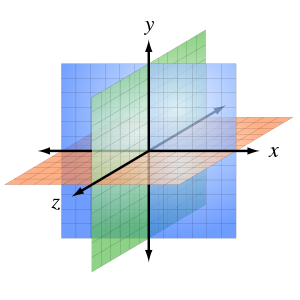Normalmente se denominan x, y, y z. En relación con estos ejes, la posición de cualquier punto en el espacio tridimensional viene dada por un triple ordenado de números reales, cada número dando la distancia de ese punto desde el origen medido a lo largo del eje dado, que es igual a la distancia de ese punto desde el plano determinado por los otros dos ejes.[3] Otros métodos populares para describir la ubicación de un punto en el espacio tridimensional incluyen coordenadas cilíndricas y coordenadas esféricas, aunque hay un número infinito de métodos posibles.Tres puntos distintos son colineales o determinan un único plano.En cambio, cuatro puntos distintos pueden ser colineales, coplanares o determinar todo el espacio.Los hiperplanos de un espacio tridimensional son los subespacios bidimensionales, es decir, los planos.Una esfera en el 3-espacio (también llamada 2-esfera porque es un objeto bidimensional) consiste en el conjunto de todos los puntos del 3-espacio a una distancia fija r de un punto central P. El sólido encerrado por la esfera se llama bola (o, más precisamente una 3-bola).En términos topológicos precisos, cada punto de la 3-esfera tiene una vecindad que es homeomorfa a un subconjunto abierto del espacio 3D.Sin embargo, si la generatriz y el eje son paralelos, entonces la superficie de revolución es un cilindro circular.En matemáticas el sistema tridimensional se representa en el plano cartesiano con los ejes X, Y y Z. Por lo general en estas representaciones se manejan las formas geométricas de tres dimensiones como los cubos o las esferas en dos dimensiones utilizando perspectivas.Hoy en día es posible la simulación mediante cálculos basados en la proyección de entornos tridimensionales sobre pantallas bidimensionales, como monitores o televisores.
Esquema elemental de posicionamiento espacial, consistente en un marco de referencia respecto a un origen dado.
