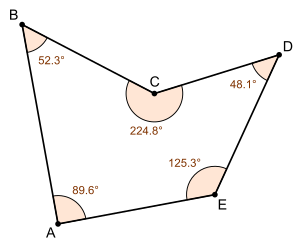
Ángulo interior

Un polígono simple tiene solo un ángulo interno por cada vértice.

En el plano euclídeo, si todos los ángulos interiores de un polígono no superan los 180 grados sexagesimales o

radianes, se clasifican como polígonos convexos.

Si existe por lo menos un ángulo interior superior a 180 grados o

radianes, se trata de un polígono cóncavo.

Si todos los ángulos interiores de un polígono simple y convexo son iguales y todos sus lados tienen la misma longitud, se trata de un polígono regular.

En caso contrario, se trata de un polígono irregular.

En general, la suma del ángulo interior en grados de cualquier polígono cerrado, incluidos los cruzados (que se intersecan a sí mismos), viene dada por 180 (n-2k)°, donde n es el número de vértices y el número no negativo k es el número de revoluciones totales de 360° que se experimentan al recorrer el perímetro.

En otras palabras, 360k° representa la suma de todos los ángulos exteriores.

Por ejemplo, para polígonos convexos y cóncavos ordinarios k=1, ya que la suma de los ángulos exteriores es 360°, y se realiza solo una revolución completa recorriendo el perímetro.