Transponer

En álgebra lineal , la transposición de una matriz es un operador $que$ voltea una matriz sobre su diagonal; es decir, intercambia los índices de fila y columna de la matriz $A$ produciendo otra matriz, a menudo denotada por $AT$ (entre otras notaciones). ^[1]

La transpuesta de una matriz fue introducida en 1858 por el matemático británico Arthur Cayley . ^[2] En el caso de una matriz lógica que representa una relación binaria R, la transpuesta corresponde a la relación inversa R ^T .

Transposición de una matriz

Definición

La transpuesta de una matriz $A$ , denotada por $A T$ , ^[3] $⊤ A$ , $A ⊤$ , , ^[4]^[5] $A'$ , ^[6] $A$ $tr$ , $t$ $A$ o $A$ $t$ , puede construirse mediante cualquiera de los siguientes métodos: $A^{\intercalar}$

Refleja $A$ sobre su diagonal principal (que va de arriba a la izquierda a abajo a la derecha) para obtener $A T$
Escribe las filas de $A$ como las columnas de $A T$
Escribe las columnas de $A$ como las filas de $A T$

Formalmente, el elemento de fila $i$ , columna $j de$ $A T$ es el elemento de fila $j , columna$ $i de$ $A$ :

\left[\mathbf {A} ^{\operatorname {T} }\right]_{ij}=\left[\mathbf {A} \right]_{ji}.

Si $A$ es una matriz $m \times n$ $, entonces AT$ $es$ una matriz $n \times m .$

En el caso de matrices cuadradas, $A T$ también puede denotar la $T$ ésima potencia de la matriz $A$ . Para evitar una posible confusión, muchos autores utilizan mayúsculas a la izquierda, es decir, denotan la transpuesta como $T A$ . Una ventaja de esta notación es que no se necesitan paréntesis cuando hay exponentes involucrados: como $(T A) n = T (A n)$ , la notación $T A n$ no es ambigua.

En este artículo se evita esta confusión al no utilizar nunca el símbolo $T$ como nombre de variable .

Definiciones de matrices que implican transposición

Una matriz cuadrada cuya transpuesta es igual a sí misma se llama matriz simétrica ; es decir, $A$ es simétrica si

\mathbf {A} ^{\operatorname {T} }=\mathbf {A} .

Una matriz cuadrada cuya transpuesta es igual a su negativo se llama matriz antisimétrica ; es decir, $A$ es antisimétrica si

\mathbf {A} ^{\operatorname {T} }=-\mathbf {A} .

Una matriz compleja cuadrada cuya transpuesta es igual a la matriz con cada entrada reemplazada por su conjugado complejo (indicado aquí con una línea superior) se llama matriz hermítica (equivalente a que la matriz sea igual a su transpuesta conjugada ); es decir, $A$ es hermítica si

\mathbf {A} ^{\operatorname {T} }={\overline {\mathbf {A} }}.

Una matriz compleja cuadrada cuya transpuesta es igual a la negación de su conjugada compleja se llama matriz antihermítica ; es decir, $A$ es antihermítica si

\mathbf {A} ^{\operatorname {T} }=-{\overline {\mathbf {A} }}.

Una matriz cuadrada cuya transpuesta es igual a su inversa se llama matriz ortogonal ; es decir, $A$ es ortogonal si

\mathbf {A} ^{\operatorname {T} }=\mathbf {A} ^{-1}.

Una matriz compleja cuadrada cuya transpuesta es igual a su inversa conjugada se llama matriz unitaria ; es decir, $A$ es unitaria si

\mathbf {A} ^{\operatorname {T} }={\overline {\mathbf {A} ^{-1}}}.

Ejemplos

${\begin{bmatrix}1&2\end{bmatrix}}^{\operatorname {T} }=\,{\begin{bmatrix}1\\2\end{bmatrix}}$

${\begin{bmatrix}1&2\\3&4\end{bmatrix}}^{\operatorname {T} }={\begin{bmatrix}1&3\\2&4\end{bmatrix}}$

${\begin{bmatrix}1&2\\3&4\\5&6\end{bmatrix}}^{\operatorname {T} }={\begin{bmatrix}1&3&5\\2&4&6\end{bmatrix}}$

Propiedades

Sean $A$ y $B$ matrices y $c$ un escalar .

$\left(\mathbf {A} ^{\operatorname {T} }\right)^{\operatorname {T} }=\mathbf {A} .$
La operación de tomar la transpuesta es una involución (autoinversa ) .
$\left(\mathbf {A} +\mathbf {B} \right)^{\operatorname {T} }=\mathbf {A} ^{\operatorname {T} }+\mathbf {B} ^{\operatorname {T} }.$
La transposición respeta la adición .
$\left(c\mathbf {A} \right)^{\operatorname {T} }=c\mathbf {A} ^{\operatorname {T} }.$
La transpuesta de un escalar es el mismo escalar. Junto con la propiedad anterior, esto implica que la transpuesta es una función lineal del espacio de matrices $m \times n$ al espacio de matrices $n \times m$ .
$\left(\mathbf {AB} \right)^{\nombredeloperador {T} }=\mathbf {B} ^{\nombredeloperador {T} }\mathbf {A} ^{\nombredeloperador {T} }.$
El orden de los factores se invierte. Por inducción, este resultado se extiende al caso general de matrices múltiples, por lo que
$(A 1 A 2 ... Ak -1 Ak) T = Ak TA k -1 T \dots A 2 T A 1 T$ . $$ $$ $$ $$
$\det \left(\mathbf {A} ^{\operatorname {T} }\right)=\det(\mathbf {A} ).$
El determinante de una matriz cuadrada es el mismo que el determinante de su transpuesta.
El producto escalar de dos vectores columna $a$ y $b$ se puede calcular como la entrada única del producto matricial $\mathbf {a} \cdot \mathbf {b} =\mathbf {a} ^{\operatorname {T} }\mathbf {b} .$
Si $A$ sólo tiene entradas reales, entonces $A T A$ es una matriz semidefinida positiva .
$\left(\mathbf {A} ^{\operatorname {T} }\right)^{-1}=\left(\mathbf {A} ^{-1}\right)^{\operatorname {T} }.$
La transpuesta de una matriz invertible también es invertible, y su inversa es la transpuesta de la inversa de la matriz original.
La notación $A -T$ se utiliza a veces para representar cualquiera de estas expresiones equivalentes.
Si $A$ es una matriz cuadrada, entonces sus valores propios son iguales a los valores propios de su transpuesta, ya que comparten el mismo polinomio característico .
Sobre cualquier campo , una matriz cuadrada es similar a . ${\estilo de visualización k}$ $\mathbf {A}$ $\mathbf {A} ^{\operatorname {T} }$
Esto implica que y tienen los mismos factores invariantes , lo que implica que comparten el mismo polinomio mínimo, polinomio característico y valores propios, entre otras propiedades. $\mathbf {A}$ $\mathbf {A} ^{\operatorname {T} }$
Una prueba de esta propiedad utiliza las dos observaciones siguientes.
- Sean y matrices sobre algún cuerpo base y sea una extensión de cuerpo de . Si y son similares como matrices sobre , entonces son similares sobre . En particular, esto se aplica cuando es el cierre algebraico de . $\mathbf {A}$ $\mathbf {B}$ $n\veces n$ ${\estilo de visualización k}$ ${\estilo de visualización L}$ ${\estilo de visualización k}$ $\mathbf {A}$ $\mathbf {B}$ ${\estilo de visualización L}$ ${\estilo de visualización k}$ ${\estilo de visualización L}$ ${\estilo de visualización k}$
- Si es una matriz sobre un cuerpo algebraicamente cerrado en forma normal de Jordan con respecto a alguna base, entonces es similar a . Esto se reduce a demostrar el mismo hecho cuando es un solo bloque de Jordan, lo cual es un ejercicio sencillo. $\mathbf {A}$ $\mathbf {A}$ $\mathbf {A} ^{\operatorname {T} }$ $\mathbf {A}$

Productos

Si $A$ es una matriz $m \times n$ $y A T$ es su transpuesta, entonces el resultado de la multiplicación de matrices con estas dos matrices da dos matrices cuadradas: $AA T$ es $m \times m$ y $A T A$ es $n \times n$ . Además, estos productos son matrices simétricas . De hecho, el producto matricial $AA T$ tiene entradas que son el producto interno de una fila de $A$ con una columna de $A T$ . Pero las columnas de $A T$ son las filas de $A$ , por lo que la entrada corresponde al producto interno de dos filas de $A$ . Si $p i j$ es la entrada del producto, se obtiene de las filas $i$ y $j$ en $A$ . La entrada $p j i$ también se obtiene de estas filas, por lo tanto $p i j = p j i$ , y la matriz producto ( $p i j$ ) es simétrica. De manera similar, el producto $A T A$ es una matriz simétrica.

Una prueba rápida de la simetría de $AA T$ resulta del hecho de que es su propia transpuesta:

\left(\mathbf {A} \mathbf {A} ^{\operadorname {T} }\right)^{\operadorname {T} }=\left(\mathbf {A} ^{\operadorname {T} }\right)^{\operadorname {T} }\mathbf {A} ^{\operadorname {T} }=\mathbf {A} \mathbf {A} ^{\operadorname {T} }.

^[7]

Implementación de la transposición de matrices en computadoras

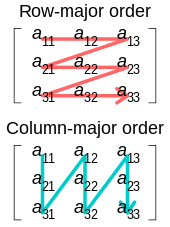
En una computadora , a menudo se puede evitar la transposición explícita de una matriz en la memoria simplemente accediendo a los mismos datos en un orden diferente. Por ejemplo, las bibliotecas de software para álgebra lineal , como BLAS , suelen proporcionar opciones para especificar que ciertas matrices se deben interpretar en orden transpuesto para evitar la necesidad de mover los datos.

Sin embargo, sigue habiendo una serie de circunstancias en las que es necesario o deseable reordenar físicamente una matriz en la memoria para que vuelva a su orden transpuesto. Por ejemplo, con una matriz almacenada en orden de fila principal , las filas de la matriz son contiguas en la memoria y las columnas son discontinuas. Si es necesario realizar operaciones repetidas en las columnas, por ejemplo en un algoritmo de transformada rápida de Fourier , la transposición de la matriz en la memoria (para que las columnas sean contiguas) puede mejorar el rendimiento al aumentar la localidad de la memoria .

Idealmente, se podría esperar transponer una matriz con un almacenamiento adicional mínimo. Esto conduce al problema de transponer una matriz n × m en el lugar , con O(1) almacenamiento adicional o, como máximo, un almacenamiento mucho menor que mn . Para n ≠ m , esto implica una permutación complicada de los elementos de datos que no es trivial de implementar en el lugar. Por lo tanto, la transposición eficiente de matrices en el lugar ha sido el tema de numerosas publicaciones de investigación en ciencias de la computación , a partir de fines de la década de 1950, y se han desarrollado varios algoritmos.

Transposiciones de aplicaciones lineales y formas bilineales

Como el uso principal de las matrices es representar mapas lineales entre espacios vectoriales de dimensión finita , la transposición es una operación sobre matrices que puede verse como la representación de alguna operación sobre mapas lineales.

Esto conduce a una definición mucho más general de la transpuesta que funciona en cualquier aplicación lineal, incluso cuando las aplicaciones lineales no se pueden representar mediante matrices (como en el caso de espacios vectoriales de dimensión infinita). En el caso de dimensión finita, la matriz que representa la transpuesta de una aplicación lineal es la transpuesta de la matriz que representa la aplicación lineal, independientemente de la elección de la base .

Transposición de una función lineal

Sea $X #$ el espacio dual algebraico de un $R$ - módulo $X$ . Sean X $e$ Y $R$ $-$ módulos. Si $u : X \to Y$ es una función lineal , entonces su adjunto algebraico o dual , ^[8] es la función $u # : Y # \to X #$ definida por $f \mapsto f \circ u$ . La función resultante $u # (f)$ se denomina pullback de $f$ por $u$ . La siguiente relación caracteriza al adjunto algebraico de $u$ ^[9]

⟨ u # ​​(f), x ⟩ = ⟨ f, u (x)⟩

para todo

f \in Y #

x \in X

donde $⟨•, •⟩$ es el emparejamiento natural (es decir, definido por $⟨ h, z ⟩ := h (z)$ ). Esta definición también se aplica sin cambios a los módulos izquierdos y a los espacios vectoriales. ^[10]

La definición de la transpuesta puede considerarse independiente de cualquier forma bilineal en los módulos, a diferencia del adjunto (abajo).

El espacio dual continuo de un espacio vectorial topológico (TVS) $X$ se denota por $X'$ . Si $X$ e $Y$ son TVS, entonces una función lineal $u : X \to Y$ es débilmente continua si y solo si $u # (Y') \subseteq X'$ , en cuyo caso dejamos $que t u : Y' \to X'$ denote la restricción de $u #$ a $Y'$ . La función $t u$ se llama transpuesta ^[11] de $u$ .

Si la matriz $A$ describe una función lineal con respecto a $las$ bases de $V$ y $W$ , entonces la matriz $AT$ describe la transpuesta de esa función lineal con respecto a las bases duales .

Transposición de una forma bilineal

Toda función lineal del espacio dual $u : X \to X #$ define una forma bilineal $B : X \times X \to F$ , con la relación $B (x, y) = u (x)(y)$ . Al definir la transpuesta de esta forma bilineal como la forma bilineal $t B$ definida por la transpuesta $t u : X ## \to X #$ es decir $t B (y, x) = t u ( Ψ(y))(x)$ , encontramos que $B (x, y) = t B (y, x)$ . Aquí, $Ψ$ es el homomorfismo natural $X \to X ##$ en el dual doble .

Adjunto

Si los espacios vectoriales $X$ e $Y$ tienen respectivamente formas bilineales no degeneradas $B$ $X$ y $B$ $Y$ , se puede definir un concepto conocido como adjunto , que está estrechamente relacionado con la transpuesta:

Si $u : X \to Y$ es una función lineal entre los espacios vectoriales $X$ e $Y$ , definimos $g$ como el adjunto de $u$ si $g : Y \to X$ satisface

B_{X}{\big (}x,g(y){\big )}=B_{Y}{\big (}u(x),y{\big )}

para todos

x \in X

y \in Y

Estas formas bilineales definen un isomorfismo entre $X$ y $X #$ , y entre $Y$ e $Y #$ , lo que da como resultado un isomorfismo entre la transpuesta y la adjunta de $u$ . La matriz de la adjunta de una función es la matriz transpuesta solo si las bases son ortonormales con respecto a sus formas bilineales. Sin embargo, en este contexto, muchos autores usan el término transpuesta para referirse a la adjunta tal como se define aquí.

El adjunto nos permite considerar si $g : Y \to X$ es igual a $u -1 : Y \to X$ . En particular, esto permite definir el grupo ortogonal sobre un espacio vectorial $X con forma cuadrática sin referencia a matrices (ni a sus componentes) como el conjunto de todas las funciones lineales$ $X \to X$ para las cuales el adjunto es igual a la inversa.

En un espacio vectorial complejo, a menudo se trabaja con formas sesquilíneas (lineales conjugadas en un argumento) en lugar de formas bilineales. El adjunto hermítico de una función entre dichos espacios se define de manera similar, y la matriz del adjunto hermítico está dada por la matriz transpuesta conjugada si las bases son ortonormales.

Véase también

Matriz adjunta , la transpuesta de la matriz cofactorial
Transposición conjugada
Pseudoinversa de Moore-Penrose
Proyección (álgebra lineal)

Referencias

^ Nykamp, Duane. "La transposición de una matriz". Math Insight . Consultado el 8 de septiembre de 2020 .
↑ Arthur Cayley (1858) "A memoir on the theory of matrices", Philosophical Transactions of the Royal Society of London , 148 : 17–37. La transposición se define en la página 31.
^ TA Whitelaw (1 de abril de 1991). Introducción al álgebra lineal, 2.ª edición. CRC Press. ISBN 978-0-7514-0159-2.
^ "Transposición de un producto matricial (ProofWiki)". ProofWiki . Consultado el 4 de febrero de 2021 .
^ "¿Cuál es el mejor símbolo para la transposición de vectores/matrices?". Stack Exchange . Consultado el 4 de febrero de 2021 .
^ Weisstein, Eric W. "Transposición". mathworld.wolfram.com . Consultado el 8 de septiembre de 2020 .
^ Gilbert Strang (2006) Álgebra lineal y sus aplicaciones , 4.ª edición, página 51, Thomson Brooks/Cole ISBN 0-03-010567-6
^ Schaefer y Wolff 1999, pág. 128.
^ Halmos 1974, §44
^ Bourbaki 1989, II §2.5
^ Trèves 2006, pág. 240.

Lectura adicional

Bourbaki, Nicolás (1989) [1970]. Álgebra I Capítulos 1-3 [ Álgebra: Capítulos 1 a 3 ] (PDF) . Elementos matemáticos . Berlín Nueva York: Springer Science & Business Media. ISBN 978-3-540-64243-5.OCLC 18588156 .

Halmos, Paul (1974), Espacios vectoriales de dimensión finita , Springer, ISBN 978-0-387-90093-3.
Maruskin, Jared M. (2012). Álgebra lineal esencial. San José: Solar Crest. págs. 122–132. ISBN 978-0-9850627-3-6.
Schaefer, Helmut H. ; Wolff, Manfred P. (1999). Espacios vectoriales topológicos . GTM . Vol. 8 (Segunda ed.). Nueva York, NY: Springer New York Imprenta Springer. ISBN 978-1-4612-7155-0.OCLC 840278135 .
Trèves, François (2006) [1967]. Espacios vectoriales topológicos, distribuciones y núcleos . Mineola, NY: Dover Publications. ISBN 978-0-486-45352-1.OCLC 853623322 .
Schwartz, Jacob T. (2001). Introducción a las matrices y vectores. Mineola: Dover. pp. 126–132. ISBN 0-486-42000-0.

Enlaces externos

Gilbert Strang (primavera de 2010) Álgebra lineal de MIT Open Courseware