La teoría de las mareas es la aplicación de la mecánica del medio continuo para interpretar y predecir las deformaciones de las mareas de los cuerpos planetarios y satelitales y sus atmósferas y océanos (especialmente los océanos de la Tierra) bajo la carga gravitacional de otro cuerpo o cuerpos astronómicos (especialmente la Luna y el Sol ).
El pueblo Yolngu del noreste de la Tierra de Arnhem en el Territorio del Norte de Australia identificó un vínculo entre la Luna y las mareas, que míticamente atribuyeron a que la Luna se llenaba de agua y se vaciaba nuevamente. [1] [2]
Las mareas recibieron relativamente poca atención en las civilizaciones alrededor del mar Mediterráneo , ya que las mareas allí son relativamente pequeñas y las áreas que las experimentan lo hacen de manera poco confiable. [3] [4] [5] Sin embargo, se propusieron varias teorías, desde comparar los movimientos con la respiración o el flujo sanguíneo hasta teorías que involucraban remolinos o ciclos fluviales. [4] Algunos pensadores asiáticos consideraron una idea similar de "tierra respiradora". [6] Se dice que Platón creía que las mareas eran causadas por el agua que entraba y salía de cavernas submarinas. [3] Crates de Mallus atribuyó las mareas al "movimiento contrario (ἀντισπασμός) del mar" y Apolodoro de Corcira a "los reflujos del océano". [7] Un antiguo texto indio Purana que data del 400-300 a. C. se refiere al ascenso y descenso del océano debido a la expansión del calor de la luz de la Luna. [a] [8]
Finalmente, los griegos descubrieron el vínculo entre la Luna (y el Sol ) y las mareas , aunque la fecha exacta del descubrimiento no está clara; hay referencias al mismo en fuentes como Piteas de Massilia en el 325 a. C. y la Historia natural de Plinio el Viejo en el 77 d. C. Aunque se conocía el calendario de las mareas y su vínculo con los movimientos lunares y solares, no estaba claro el mecanismo exacto que los conectaba. [4] El clasicista Thomas Little Heath afirmó que tanto Piteas como Posidonio relacionaban las mareas con la luna, "el primero directamente, el segundo a través del establecimiento de vientos". [7] Séneca menciona en De Providentia el movimiento periódico de las mareas controlado por la esfera lunar. [9] Eratóstenes (siglo III a. C.) y Posidonio (siglo I a. C.) produjeron descripciones detalladas de las mareas y su relación con las fases de la luna ; Posidonio en particular hizo largas observaciones del mar en la costa española, aunque poco de su trabajo sobrevivió. La influencia de la Luna en las mareas fue mencionada en el Tetrabiblos de Ptolomeo como evidencia de la realidad de la astrología . [3] [10] Se cree que Seleuco de Seleucia teorizó alrededor del 150 a. C. que las mareas eran causadas por la Luna como parte de su modelo heliocéntrico . [11] [12]
Aristóteles , a juzgar por las discusiones sobre sus creencias en otras fuentes, se cree que creía que las mareas eran causadas por vientos impulsados por el calor del Sol, y rechazó la teoría de que la Luna causaba las mareas. Una leyenda apócrifa afirma que se suicidó frustrado por su incapacidad para comprender completamente las mareas. [3] Heráclides también sostuvo que "el sol crea vientos, y que estos vientos, cuando soplan, causan la marea alta y, cuando cesan, la marea baja". [7] Dicearco también "atribuyó las mareas a la acción directa del sol según su posición". [7] Filóstrato analiza las mareas en el Libro Cinco de la Vida de Apolonio de Tiana (circa 217-238 d. C.); era vagamente consciente de una correlación de las mareas con las fases de la Luna, pero las atribuyó a espíritus que movían agua dentro y fuera de las cavernas, lo que relacionó con la leyenda de que los espíritus de los muertos no pueden moverse en ciertas fases de la Luna. [b]
Beda el Venerable analiza las mareas en El cálculo del tiempo y muestra que el hecho de que las mareas se produzcan dos veces al día está relacionado con la Luna y que el ciclo lunar mensual de mareas vivas y muertas también está relacionado con la posición de la Luna. Continúa señalando que los tiempos de las mareas varían a lo largo de la misma costa y que los movimientos del agua causan mareas bajas en un lugar cuando hay mareas altas en otro. [13] Sin embargo, no hizo ningún progreso en cuanto a la cuestión de cómo exactamente la Luna crea las mareas. [4]
Se decía que los métodos empíricos medievales para predecir las mareas permitían "saber qué luna produce marea alta" a partir de los movimientos de la luna. [14] Dante hace referencia a la influencia de la luna en las mareas en su Divina Comedia . [15] [3]
La comprensión medieval europea de las mareas se basaba a menudo en obras de astrónomos musulmanes que estuvieron disponibles a través de traducciones latinas a partir del siglo XII. [16] Abu Ma'shar al-Balkhi , en su Introductorium in astronomiam , enseñó que las mareas de reflujo y de inundación eran causadas por la Luna. [16] Abu Ma'shar discutió los efectos del viento y las fases de la Luna en relación con el Sol en las mareas. [16] En el siglo XII, al-Bitruji contribuyó con la noción de que las mareas eran causadas por la circulación general de los cielos. [16] Los astrólogos árabes medievales frecuentemente hacían referencia a la influencia de la Luna en las mareas como evidencia de la realidad de la astrología; algunos de sus tratados sobre el tema influyeron en Europa occidental. [10] [3] Algunos teorizaron que la influencia era causada por los rayos lunares que calentaban el fondo del océano. [5]
Simon Stevin en su obra De spiegheling der Ebbenvloet (La teoría del reflujo y la inundación ) de 1608 descarta una gran cantidad de conceptos erróneos que aún existían sobre el reflujo y la inundación. Stevin aboga por la idea de que la atracción de la Luna era responsable de las mareas y escribe en términos claros sobre el reflujo, la inundación, la marea viva y la marea muerta, enfatizando que era necesario realizar más investigaciones. [17] [18] En 1609, Johannes Kepler sugirió correctamente que la gravitación de la Luna causa las mareas, [c] que comparó con la atracción magnética [20] [4] [21] [22] basando su argumento en antiguas observaciones y correlaciones.
En 1616, Galileo Galilei escribió Discurso sobre las mareas . [23] Rechaza enérgicamente y en tono burlón la teoría lunar de las mareas, [21] [4] e intenta explicar las mareas como resultado de la rotación y revolución de la Tierra alrededor del Sol , creyendo que los océanos se movían como el agua en una gran cuenca: a medida que la cuenca se mueve, también lo hace el agua. [24] Por lo tanto, a medida que la Tierra gira, la fuerza de rotación de la Tierra hace que los océanos se "aceleren y retarden alternativamente". [25] Su visión sobre la oscilación y el movimiento "alternativamente acelerado y retardado" de la rotación de la Tierra es un "proceso dinámico" que se desviaba del dogma anterior, que proponía "un proceso de expansión y contracción del agua de mar". [26] Sin embargo, la teoría de Galileo era errónea. [23] En siglos posteriores, análisis posteriores condujeron a la actual física de las mareas. Galileo intentó utilizar su teoría de las mareas para demostrar el movimiento de la Tierra alrededor del Sol. Galileo teorizó que debido al movimiento de la Tierra, las fronteras de los océanos como el Atlántico y el Pacífico mostrarían una marea alta y una marea baja por día. El mar Mediterráneo tenía dos mareas altas y dos mareas bajas, aunque Galileo argumentó que esto era producto de efectos secundarios y que su teoría se mantendría en el Atlántico. Sin embargo, los contemporáneos de Galileo notaron que el Atlántico también tenía dos mareas altas y dos mareas bajas por día, lo que llevó a Galileo a omitir esta afirmación en su Diálogo de 1632. [ 27 ]
René Descartes teorizó que las mareas (junto con el movimiento de los planetas, etc.) eran causadas por vórtices etéricos , sin hacer referencia a las teorías de Kepler sobre la gravitación por atracción mutua; esto fue extremadamente influyente, con numerosos seguidores de Descartes exponiendo esta teoría a lo largo del siglo XVII, particularmente en Francia. [28] Sin embargo, Descartes y sus seguidores reconocieron la influencia de la Luna, especulando que las ondas de presión de la Luna a través del éter eran responsables de la correlación. [5] [29] [6] [30]
Newton , en los Principia , proporciona una explicación correcta de la fuerza de marea , que puede utilizarse para explicar las mareas en un planeta cubierto por un océano uniforme, pero que no tiene en cuenta la distribución de los continentes ni la batimetría del océano . [31]
Mientras que Newton explicó las mareas describiendo las fuerzas generadoras de mareas y Daniel Bernoulli dio una descripción de la reacción estática de las aguas de la Tierra al potencial de marea, la teoría dinámica de las mareas , desarrollada por Pierre-Simon Laplace en 1775, [32] describe la reacción real del océano a las fuerzas de marea. [33] La teoría de las mareas oceánicas de Laplace tiene en cuenta la fricción , la resonancia y los períodos naturales de las cuencas oceánicas. Predice los grandes sistemas anfidrómicos en las cuencas oceánicas del mundo y explica las mareas oceánicas que se observan realmente. [34]
La teoría del equilibrio, basada en el gradiente gravitacional del Sol y la Luna pero que ignora la rotación de la Tierra, los efectos de los continentes y otros efectos importantes, no podía explicar las mareas oceánicas reales. [35] Dado que las mediciones han confirmado la teoría dinámica, muchas cosas tienen ahora explicaciones posibles, como la forma en que las mareas interactúan con las dorsales marinas profundas y las cadenas de montes submarinos dan lugar a remolinos profundos que transportan nutrientes desde las profundidades hasta la superficie. [36] La teoría de la marea de equilibrio calcula la altura de la ola de marea en menos de medio metro, mientras que la teoría dinámica explica por qué las mareas alcanzan los 15 metros. [37]
Las observaciones satelitales confirman la precisión de la teoría dinámica, y las mareas en todo el mundo ahora se miden con una precisión de unos pocos centímetros. [38] [39] Las mediciones del satélite CHAMP coinciden estrechamente con los modelos basados en los datos TOPEX . [40] [41] [42] Los modelos precisos de mareas en todo el mundo son esenciales para la investigación, ya que las variaciones debidas a las mareas deben eliminarse de las mediciones al calcular la gravedad y los cambios en los niveles del mar. [43]
En 1776, Laplace formuló un único conjunto de ecuaciones diferenciales parciales lineales para el flujo de mareas, descrito como un flujo laminar barotrópico bidimensional. Se introducen los efectos de Coriolis , así como la fuerza lateral por gravedad . Laplace obtuvo estas ecuaciones simplificando las ecuaciones de dinámica de fluidos , pero también se pueden derivar de integrales de energía mediante la ecuación de Lagrange .
Para una lámina de fluido de espesor promedio D , la elevación de marea vertical ζ , así como los componentes de velocidad horizontal u y v (en las direcciones de latitud φ y longitud λ , respectivamente) satisfacen las ecuaciones de marea de Laplace : [44]
donde Ω es la frecuencia angular de rotación del planeta, g es la aceleración gravitacional del planeta en la superficie media del océano, a es el radio planetario y U es el potencial de fuerza de marea gravitacional externa .
William Thomson (Lord Kelvin) reescribió los términos de momento de Laplace utilizando el rotacional para hallar una ecuación para la vorticidad . En determinadas condiciones, esta ecuación puede reescribirse como una conservación de la vorticidad.
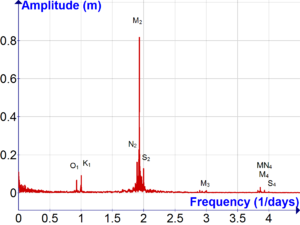
Las mejoras teóricas de Laplace fueron sustanciales, pero aún dejaban la predicción en un estado aproximado. Esta situación cambió en la década de 1860 cuando William Thomson aplicó el análisis de Fourier a los movimientos de marea como análisis armónico y tuvo más en cuenta las circunstancias locales de los fenómenos de marea . El trabajo de Thomson en este campo fue desarrollado y ampliado por George Darwin , que aplicó la teoría lunar vigente en su época. Los símbolos de Darwin para los componentes armónicos de las mareas todavía se utilizan.
Los desarrollos armónicos de Darwin de las fuerzas generadoras de mareas fueron mejorados posteriormente cuando AT Doodson , aplicando la teoría lunar de EW Brown , [45] desarrolló el potencial generador de mareas (TGP) en forma armónica, distinguiendo 388 frecuencias de marea. [46] El trabajo de Doodson se llevó a cabo y publicó en 1921. [47] Doodson ideó un sistema práctico para especificar los diferentes componentes armónicos del potencial generador de mareas, los números de Doodson , un sistema todavía en uso.
Desde mediados del siglo XX, los análisis posteriores han generado muchos más términos que los 388 de Doodson. Aproximadamente 62 constituyentes tienen un tamaño suficiente para ser considerados para su posible uso en la predicción de mareas marinas, pero a veces muchos menos pueden predecir mareas con una precisión útil. Los cálculos de predicciones de mareas utilizando los constituyentes armónicos son laboriosos y, desde la década de 1870 hasta aproximadamente la década de 1960, se llevaron a cabo utilizando una máquina mecánica de predicción de mareas , una forma especial de computadora analógica . Más recientemente, se utilizan computadoras digitales, utilizando el método de inversión de matrices, para determinar los constituyentes armónicos de marea directamente a partir de los registros de mareógrafos.
Los componentes de las mareas se combinan para dar un agregado que varía infinitamente debido a sus frecuencias diferentes e inconmensurables: el efecto se visualiza en una animación de la American Mathematical Society que ilustra la forma en que los componentes solían combinarse mecánicamente en la máquina de predicción de mareas. A continuación se muestran las amplitudes (la mitad de la amplitud de pico a pico ) de los componentes de las mareas para seis ubicaciones de ejemplo: Eastport, Maine (ME), [48] Biloxi, Mississippi (MS), San Juan, Puerto Rico (PR), Kodiak, Alaska (AK), San Francisco, California (CA) y Hilo, Hawaii (HI).
Para especificar los diferentes componentes armónicos del potencial generador de mareas, Doodson ideó un sistema práctico que todavía se utiliza y que implica lo que se denominan números de Doodson basados en los seis argumentos de Doodson o variables de Doodson. El número de diferentes componentes de frecuencia de marea es grande, pero cada uno corresponde a una combinación lineal específica de seis frecuencias utilizando múltiplos enteros pequeños, positivos o negativos. En principio, estos argumentos angulares básicos se pueden especificar de numerosas maneras; la elección de Doodson de sus seis "argumentos de Doodson" se ha utilizado ampliamente en el estudio de las mareas. En términos de estos argumentos de Doodson, cada frecuencia de marea se puede especificar como una suma formada por un múltiplo entero pequeño de cada uno de los seis argumentos. Los seis multiplicadores enteros pequeños resultantes codifican efectivamente la frecuencia del argumento de marea en cuestión, y estos son los números de Doodson: en la práctica, todos, excepto el primero, suelen estar sesgados hacia arriba en +5 para evitar números negativos en la notación. (En el caso de que el múltiplo sesgado exceda 9, el sistema adopta X para 10 y E para 11.) [49]
Los argumentos de Doodson se especifican de la siguiente manera, en orden de frecuencia decreciente: [49]
En estas expresiones, los símbolos , , y se refieren a un conjunto alternativo de argumentos angulares fundamentales (generalmente preferidos para su uso en la teoría lunar moderna), en los que:
Es posible definir varias variables auxiliares en base a combinaciones de éstas.
En términos de este sistema, cada frecuencia constituyente de marea puede identificarse por sus números Doodson. El constituyente de marea más fuerte "M 2 " tiene una frecuencia de 2 ciclos por día lunar, sus números Doodson se escriben generalmente 255.555, lo que significa que su frecuencia está compuesta por el doble del primer argumento Doodson, y cero veces todos los demás. El segundo constituyente de marea más fuerte "S 2 " está influenciado por el sol, y sus números Doodson son 273.555, lo que significa que su frecuencia está compuesta por el doble del primer argumento Doodson, +2 veces el segundo, -2 veces el tercero, y cero veces cada uno de los otros tres. [50] Esto se suma al equivalente angular del tiempo solar medio +12 horas. Estas dos frecuencias componentes más fuertes tienen argumentos simples para los cuales el sistema Doodson podría parecer innecesariamente complejo, pero cada una de las cientos de otras frecuencias componentes se puede especificar brevemente de una manera similar, mostrando en conjunto la utilidad de la codificación.
![{\displaystyle {\begin{aligned}{\frac {\partial \zeta }{\partial \lambda }}&+{\frac {1}{a\cos(\varphi )}}\left[{\frac {\partial }{\partial \lambda }}(uD)+{\frac {\partial }{\partial \varphi }}\left(vD\cos(\varphi )\right)\right]=0,\\[2ex]{\frac {\partial u}{\partial t}}&-v\,2\Omega \sin(\varphi )+{\frac {1}{a\cos(\varphi )}}{\frac {\partial }{\partial \lambda }}\left(g\zeta +U\right)=0,\quad {\text{y}}\\[2ex]{\frac {\partial v}{\partial t}}&+u\,2\Omega \sin(\varphi )+{\frac {1}{a}}{\frac {\partial }{\partial \varphi }}\left(g\zeta +U\right)=0,\end{alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93fa08ee6fd9993a354e58f22257c7847c90666d)
