Griegos (finanzas)

Parámetros del modelo en finanzas matemáticas.

En finanzas matemáticas , los griegos son las cantidades (conocidas en cálculo como derivados parciales ; de primer orden o superior) que representan la sensibilidad del precio de un instrumento derivado , como una opción , a los cambios en uno o más parámetros subyacentes sobre los cuales se determina el valor de un instrumento o cartera de instrumentos financieros es dependiente. El nombre se utiliza porque las sensibilidades más comunes se indican con letras griegas (al igual que algunas otras medidas financieras). En conjunto, también se les ha denominado sensibilidades al riesgo , ^[1] medidas de riesgo ^{[2] : 742} o parámetros de cobertura . ^[3]

Uso de los griegos

Los griegos son herramientas vitales en la gestión de riesgos . Cada griego mide la sensibilidad del valor de una cartera a un pequeño cambio en un parámetro subyacente determinado, de modo que los riesgos de los componentes puedan tratarse de forma aislada y la cartera reequilibrarse en consecuencia para lograr la exposición deseada; véase, por ejemplo, cobertura delta .

Los griegos del modelo Black-Scholes (un modelo idealizado relativamente simple de ciertos mercados financieros) son relativamente fáciles de calcular (una propiedad deseable de los modelos financieros ) y son muy útiles para los operadores de derivados, especialmente aquellos que buscan proteger sus carteras de situaciones adversas. cambios en las condiciones del mercado. Por esta razón, aquellos griegos que son particularmente útiles para la cobertura (como delta, theta y vega) están bien definidos para medir cambios en los parámetros precio al contado, tiempo y volatilidad. Aunque rho (la derivada parcial con respecto a la tasa de interés libre de riesgo ) es un insumo principal en el modelo de Black-Scholes, el impacto general sobre el valor de una opción a corto plazo correspondiente a los cambios en la tasa de interés libre de riesgo es generalmente insignificantes y, por lo tanto, los derivados de orden superior que involucran la tasa de interés libre de riesgo no son comunes.

Los más comunes entre los griegos son los derivados de primer orden: delta, vega, theta y rho; así como gamma, una derivada de segundo orden de la función de valor. Las sensibilidades restantes en esta lista son lo suficientemente comunes como para tener nombres comunes, pero esta lista no es de ninguna manera exhaustiva.

Los actores del mercado realizan operaciones competitivas que implican muchos miles de millones (de dólares, libras o euros) de subyacente cada día, por lo que es importante acertar con las sumas. En la práctica utilizarán modelos más sofisticados que van más allá de los supuestos simplificadores utilizados en el modelo de Black-Scholes y, por tanto, en el de los griegos.

Nombres

El uso de nombres de letras griegas es presumiblemente una extensión de los términos financieros comunes alfa y beta , y el uso de sigma (la desviación estándar de los rendimientos logarítmicos) y tau (tiempo hasta el vencimiento) en el modelo de valoración de opciones de Black-Scholes . Se inventan varios nombres como "vega" (cuyo símbolo es similar a la letra griega minúscula nu ; el uso de ese nombre podría haber llevado a confusión) y "zomma", pero suenan similares a las letras griegas. Los nombres "color" y "encanto" probablemente derivan del uso de estos términos para designar propiedades exóticas de los quarks en la física de partículas .

Griegos de primer orden

Delta

Delta , ^[4] , mide la tasa de cambio del valor teórico de la opción con respecto a los cambios en el precio del activo subyacente. Delta es la primera derivada del valorde la opción con respecto al precio del instrumento subyacente. ${\displaystyle \Delta }$ ${\displaystyle V}$ ${\displaystyle S}$

${\displaystyle \Delta ={\frac {\partial V}{\partial S}}}$

Uso práctico

Para una opción básica, delta será un número entre 0,0 y 1,0 para una opción de compra larga (o una opción de venta corta) y 0,0 y −1,0 para una opción de venta larga (o una opción de compra corta); Dependiendo del precio, una opción de compra se comporta como si uno poseyera 1 acción de la acción subyacente (si tiene mucho dinero), o no posee nada (si está muy lejos del dinero), o algo intermedio, y viceversa para una opción de venta. La diferencia entre el delta de una call y el delta de una put en el mismo strike es igual a uno. Por paridad put-call , una opción call larga y una opción put corta equivalen a un forward F , que es lineal en el spot S, con factor unitario, por lo que la derivada dF/dS es 1. Consulte las fórmulas siguientes.

Estos números comúnmente se presentan como un porcentaje del número total de acciones representadas por los contratos de opción. Esto es conveniente porque la opción se comportará (instantáneamente) como el número de acciones indicado por el delta. Por ejemplo, si una cartera de 100 opciones de compra estadounidenses sobre XYZ tiene cada una un delta de 0,25 (= 25%), ganará o perderá valor al igual que 2500 acciones de XYZ a medida que el precio cambie para pequeños movimientos de precios (100 contratos de opciones cubren 10.000 acciones). El signo y el porcentaje a menudo se omiten: el signo está implícito en el tipo de opción (negativo para la opción de venta, positivo para la opción de compra) y se entiende el porcentaje. Los más comúnmente cotizados son 25 delta put, 50 delta put/50 delta call y 25 delta call. 50 Delta put y 50 Delta call no son del todo idénticos, debido a que el spot y el forward difieren por el factor de descuento, pero a menudo se combinan.

Delta siempre es positiva para opciones de compra largas y negativa para opciones de venta largas (a menos que sean cero). El delta total de una cartera compleja de posiciones sobre el mismo activo subyacente se puede calcular simplemente tomando la suma de los deltas para cada posición individual; el delta de una cartera es lineal en los componentes. Dado que el delta del activo subyacente es siempre 1,0, el operador podría cubrir delta toda su posición en el subyacente comprando o vendiendo en corto el número de acciones indicadas por el delta total. Por ejemplo, si el delta de una cartera de opciones en XYZ (expresado como acciones del subyacente) es +2,75, el operador podría cubrir delta la cartera vendiendo en corto 2,75 acciones del subyacente. Esta cartera conservará su valor total independientemente de en qué dirección se mueva el precio de XYZ. (Aunque sólo se trate de pequeños movimientos del subyacente, en un corto período de tiempo y a pesar de los cambios en otras condiciones del mercado, como la volatilidad y la tasa de rendimiento de una inversión libre de riesgo).

Como proxy de la probabilidad

El (valor absoluto de) Delta está cerca, pero no es idéntico, al porcentaje de dinero de una opción, es decir, la probabilidad implícita de que la opción expire en el dinero (si el mercado se mueve bajo el movimiento browniano en la curva de riesgo) . medida neutral ). ^[5] Por esta razón, algunos operadores de opciones utilizan el valor absoluto de delta como una aproximación al porcentaje de dinero. Por ejemplo, si una opción de compra fuera del dinero tiene un delta de 0,15, el operador podría estimar que la opción tiene aproximadamente un 15% de posibilidades de vencer dentro del dinero. De manera similar, si un contrato de venta tiene un delta de −0,25, el operador podría esperar que la opción tenga un 25% de probabilidad de vencer en el dinero. Las opciones de compra y venta at-the-money tienen un delta de aproximadamente 0,5 y −0,5 respectivamente, con un ligero sesgo hacia deltas más altos para las llamadas en cajeros automáticos, ya que la tasa libre de riesgo introduce cierta compensación al delta. La probabilidad real de que una opción termine en dinero es su doble delta, que es la primera derivada del precio de la opción con respecto al ejercicio. ^[6]

Relación entre call y put delta

Dada una opción de compra y venta europea para el mismo subyacente, precio de ejercicio y tiempo hasta el vencimiento, y sin rendimiento por dividendo, la suma de los valores absolutos del delta de cada opción será 1; más precisamente, el delta de la opción de compra ( positivo) menos el delta de la opción de venta (negativa) es igual a 1. Esto se debe a la paridad de opción de compra y venta : una opción de compra larga más una opción de venta corta (una opción de compra menos una opción de venta) replica un forward, que tiene un delta igual a 1.

Si se conoce el valor del delta de una opción, se puede calcular el valor del delta de la opción del mismo precio de ejercicio, subyacente y vencimiento pero derecho opuesto restando 1 de un delta de compra conocido o sumando 1 a un delta de venta conocido. .

${\displaystyle \Delta ({\text{call}})-\Delta ({\text{put}})=1,{\text{ therefore: }}\Delta ({\text{call}})=\Delta ({\text{put}})+1{\text{ and }}\Delta ({\text{put}})=\Delta ({\text{call}})-1.}$

Por ejemplo, si el delta de una opción de compra es 0,42, entonces se puede calcular el delta de la opción de venta correspondiente al mismo precio de ejercicio mediante 0,42 − 1 = −0,58. Para derivar el delta de una llamada de una venta, de manera similar se puede tomar −0,58 y agregar 1 para obtener 0,42.

vega

Vega ^[4] mide la sensibilidad a la volatilidad . Vega es la derivada del valor de la opción con respecto a la volatilidad del activo subyacente.

${\displaystyle {\mathcal {V}}={\frac {\partial V}{\partial \sigma }}}$

Vega no es el nombre de ninguna letra griega. El glifo utilizado es una versión mayúscula no estándar de la letra griega nu ( ), escrita como . Presumiblemente, el nombre vega se adoptó porque la letra griega nu parecía una vee latina , y vega se derivó de vee por analogía con cómo se pronuncian beta , eta y theta en inglés americano. ${\textstyle \nu }$ ${\displaystyle {\mathcal {V}}}$

El símbolo kappa , a veces se utiliza (por académicos) en lugar de vega (como lo es tau ( ) o lambda mayúscula ( ), ^{[7] : 315} , aunque son raros). ${\displaystyle \kappa }$ ${\displaystyle \tau }$ ${\displaystyle \Lambda }$

Vega generalmente se expresa como la cantidad de dinero por acción subyacente que el valor de la opción ganará o perderá a medida que la volatilidad aumenta o disminuye en 1 punto porcentual . Todas las opciones (tanto de compra como de venta) ganarán valor a medida que aumente la volatilidad.

Vega puede ser un griego importante a seguir para un operador de opciones, especialmente en mercados volátiles, ya que el valor de algunas estrategias de opciones puede ser particularmente sensible a los cambios en la volatilidad. El valor de una opción at-the-money , por ejemplo, depende en gran medida de los cambios en la volatilidad. Ver Riesgo de volatilidad .

theta

Theta , ^[4] , mide la sensibilidad del valor de la derivada al paso del tiempo (ver Opción valor tiempo ): la "caída del tiempo". ${\displaystyle \Theta }$

${\displaystyle \Theta =-{\frac {\partial V}{\partial \tau }}}$

A medida que pasa el tiempo, con un tiempo de vencimiento cada vez menor y todo lo demás igual, el valor extrínseco de una opción disminuye. Normalmente (pero ver más abajo), esto significa que una opción pierde valor con el tiempo, lo que convencionalmente se conoce como opciones largas que generalmente tienen theta corta (negativa). De hecho, normalmente, la primera derivada literal respecto del tiempo del valor de una opción es un número positivo . El cambio en el valor de la opción suele ser negativo porque el paso del tiempo es un número negativo (una disminución del tiempo hasta el vencimiento). Sin embargo, por convención, los profesionales generalmente prefieren referirse a la exposición theta ("decaimiento") de una opción larga como negativa (en lugar del paso del tiempo como negativo), por lo que theta generalmente se informa como -1 veces la primera derivada, como arriba. ${\displaystyle \tau \,}$

Si bien el valor extrínseco disminuye con el paso del tiempo, a veces un factor compensatorio es el descuento. Para opciones con mucho dinero de algunos tipos (para opciones de venta en Black-Scholes, opciones de venta y opciones de compra en Black's), a medida que los factores de descuento aumentan hacia 1 con el paso del tiempo, ese es un elemento de valor creciente en una opción larga. . A veces, las opciones con mucho dinero ganarán más con el aumento de los factores de descuento de lo que perderán con la disminución del valor extrínseco, y theta informado será un valor positivo para una opción larga en lugar de un valor negativo más típico (y la opción será un candidato de ejercicio anticipado, si se puede ejercer, y una opción europea puede llegar a valer menos que la paridad).

Por convención, en las fórmulas de valoración de opciones, el tiempo hasta el vencimiento se define en años. Los profesionales suelen preferir ver theta en términos de cambio en el número de días hasta el vencimiento en lugar de número de años hasta el vencimiento. Por lo tanto, la theta informada generalmente se divide por el número de días de un año. (El contar los días calendario o los días hábiles varía según la elección personal, con argumentos para ambos). ${\displaystyle \tau \,}$

rho

Rho , ^[4] , mide la sensibilidad al tipo de interés: es la derivada del valor de la opción con respecto al tipo de interés libre de riesgo (para el plazo pendiente correspondiente). ${\displaystyle \rho }$

${\displaystyle \rho ={\frac {\partial V}{\partial r}}}$

Excepto en circunstancias extremas, el valor de una opción es menos sensible a cambios en la tasa de interés libre de riesgo que a cambios en otros parámetros. Por esta razón, rho es el menos utilizado de los griegos de primer orden.

Rho generalmente se expresa como la cantidad de dinero, por acción del subyacente, que el valor de la opción ganará o perderá a medida que la tasa de interés libre de riesgo suba o baje un 1,0% anual (100 puntos básicos).

lambda

Lambda , ^[4] , omega , ^[8] o elasticidad ^[4] es el cambio porcentual en el valor de la opción por cambio porcentual en el precio subyacente, una medida de apalancamiento , a veces llamado apalancamiento. ${\displaystyle \lambda }$ ${\displaystyle \Omega }$

${\displaystyle \lambda =\Omega ={\frac {\partial V}{\partial S}}\times {\frac {S}{V}}}$

Eso lo sostiene . ${\displaystyle \lambda =\Omega =\Delta \times {\frac {S}{V}}}$

Es similar al concepto de delta pero expresado en términos porcentuales en lugar de términos absolutos.

Épsilon

Epsilon , ^[9] (también conocido como psi,), es el cambio porcentual en el valor de la opción por cambio porcentual en el rendimiento de dividendos subyacente, una medida del riesgo de dividendos. El impacto en el rendimiento de los dividendos se determina en la práctica utilizando un aumento del 10% en esos rendimientos. Evidentemente, esta sensibilidad sólo puede aplicarse a instrumentos derivados de productos de renta variable . ${\displaystyle \varepsilon }$ ${\displaystyle \psi }$

${\displaystyle \varepsilon =\psi ={\frac {\partial V}{\partial q}}}$

Numéricamente, todas las sensibilidades de primer orden pueden interpretarse como diferenciales en los rendimientos esperados. ^[10] La geometría de la información ofrece otra interpretación (trigonométrica). ^[10]

Griegos de segundo orden

Gama

Gamma , ^[4] , mide la tasa de cambio en el delta con respecto a los cambios en el precio subyacente. Gamma es la segunda derivada de la función de valor con respecto al precio subyacente. ${\displaystyle \Gamma }$

${\displaystyle \Gamma ={\frac {\partial \Delta }{\partial S}}={\frac {\partial ^{2}V}{\partial S^{2}}}}$

La mayoría de las opciones largas tienen gamma positiva y la mayoría de las opciones cortas tienen gamma negativa. Las opciones largas tienen una relación positiva con gamma porque a medida que aumenta el precio, Gamma también aumenta, lo que hace que Delta se acerque a 1 desde 0 (opción de compra larga) y a 0 desde −1 (opción de venta larga). Lo contrario ocurre con las opciones cortas. ^[11]

Delta de opciones largas, precio subyacente y gamma. ^[12]

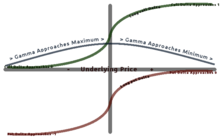
Gamma es mayor aproximadamente en el dinero (ATM) y disminuye cuanto más se aleja, ya sea dentro del dinero (ITM) o fuera del dinero (OTM). Gamma es importante porque corrige la convexidad del valor.

Cuando un operador busca establecer una cobertura delta eficaz para una cartera, también puede intentar neutralizar la gamma de la cartera, ya que esto garantizará que la cobertura sea eficaz en una gama más amplia de movimientos de precios subyacentes.

vanna

Vanna , ^[4] también conocida como DvegaDspot ^[13] y DdeltaDvol , ^[13] es un derivado de segundo orden del valor de la opción, una vez al precio spot subyacente y otra vez a la volatilidad. Es matemáticamente equivalente a DdeltaDvol , la sensibilidad de la opción delta con respecto al cambio en la volatilidad; o alternativamente, la parcial de vega respecto del precio del instrumento subyacente. Vanna puede ser una sensibilidad útil para monitorear cuando se mantiene una cartera con cobertura delta o vega, ya que ayudará al operador a anticipar cambios en la efectividad de una cobertura delta a medida que cambia la volatilidad o la efectividad de una cobertura vega contra cambios en la precio spot subyacente.

Si el valor subyacente tiene segundas derivadas parciales continuas, entonces ${\displaystyle {\text{Vanna}}={\frac {\partial \Delta }{\partial \sigma }}={\frac {\partial {\mathcal {V}}}{\partial S}}={\frac {\partial ^{2}V}{\partial S\,\partial \sigma }}.}$

Encanto

Charm ^[4] o desintegración delta ^[14] mide la tasa instantánea de cambio de delta con el paso del tiempo.

${\displaystyle {\text{Charm}}=-{\frac {\partial \Delta }{\partial \tau }}={\frac {\partial \Theta }{\partial S}}=-{\frac {\partial ^{2}V}{\partial \tau \,\partial S}}}$

Charm también ha sido llamado DdeltaDtime . ^[13] El encanto puede ser un elemento importante para medir/monitorear cuando se cubre una posición con delta durante un fin de semana. Charm es una derivada de segundo orden del valor de la opción, una vez al precio y otra al paso del tiempo. También es entonces la derivada de theta con respecto al precio del subyacente.

El resultado matemático de la fórmula de charm (ver más abajo) se expresa en delta/año. A menudo resulta útil dividir esto por el número de días por año para llegar a la desintegración delta por día. Este uso es bastante preciso cuando el número de días que quedan hasta el vencimiento de la opción es grande. Cuando una opción se acerca al vencimiento, el encanto mismo puede cambiar rápidamente, lo que hace que las estimaciones de la caída del delta de todo el día sean inexactas.

vomma

Vomma , ^[4] volga , ^[15] convexidad de vega , ^[15] o DvegaDvol ^[15] mide la sensibilidad de segundo orden a la volatilidad . Vomma es la segunda derivada del valor de la opción con respecto a la volatilidad o, dicho de otra manera, vomma mide la tasa de cambio a vega a medida que cambia la volatilidad.

${\displaystyle {\text{Vomma}}={\frac {\partial {\mathcal {V}}}{\partial \sigma }}={\frac {\partial ^{2}V}{\partial \sigma ^{2}}}}$

Con vomma positivo, una posición se convertirá en vega larga a medida que aumenta la volatilidad implícita y en vega corta a medida que disminuye, lo que se puede vender de forma análoga a la gamma larga. Y se puede construir una posición inicialmente vega-neutral y de vomma larga a partir de ratios de opciones en diferentes strikes. Vomma es positivo para opciones largas alejadas del dinero e inicialmente aumenta con la distancia del dinero (pero cae a medida que cae vega). (Específicamente, vomma es positivo cuando los términos habituales d ₁ y d ₂ son del mismo signo, lo cual es cierto cuando d ₁  < 0 o d ₂  > 0.)

veta

Veta ^[16] o DvegaDtime ^[15] mide la tasa de cambio de la vega con respecto al paso del tiempo. Veta es la segunda derivada de la función de valor; una vez a la volatilidad y otra al tiempo.

${\displaystyle {\text{Veta}}={\frac {\partial {\mathcal {V}}}{\partial \tau }}={\frac {\partial ^{2}V}{\partial \sigma \,\partial \tau }}}$

Es una práctica común dividir el resultado matemático de veta por 100 veces el número de días por año para reducir el valor al cambio porcentual en vega por día.

vera

Vera ^[17] (a veces rhova ) ^[17] mide la tasa de cambio en rho con respecto a la volatilidad. Vera es la segunda derivada de la función de valor; una vez a la volatilidad y otra a la tasa de interés.

${\displaystyle {\text{Vera}}={\frac {\partial \rho }{\partial \sigma }}={\frac {\partial ^{2}V}{\partial \sigma \,\partial r}}}$

La palabra "Vera" fue acuñada por R. Naryshkin a principios de 2012 cuando era necesario utilizar esta sensibilidad en la práctica para evaluar el impacto de los cambios de volatilidad en la cobertura rho, pero aún no existía ningún nombre en la literatura disponible. Se eligió 'Vera' para que sonara similar a una combinación de Vega y Rho, sus respectivos griegos de primer orden. Este nombre ahora tiene un uso más amplio, incluido, por ejemplo, el software de álgebra informática Maple (que tiene la función 'BlackScholesVera' en su paquete de Finanzas).

Derivada parcial de segundo orden con respecto al ejercicio K

Esta derivada parcial tiene un papel fundamental en la fórmula de Breeden-Litzenberger, ^[18] que utiliza precios cotizados de opciones de compra para estimar las probabilidades neutrales al riesgo implícitas en dichos precios.

${\displaystyle \varpi ={\frac {\partial ^{2}V}{\partial K^{2}}}}$

Para las opciones de compra, se puede aproximar utilizando carteras infinitesimales de estrategias mariposa .

Griegos de tercer orden

Velocidad

La velocidad ^[4] mide la tasa de cambio en Gamma con respecto a los cambios en el precio subyacente.

${\displaystyle {\text{Speed}}={\frac {\partial \Gamma }{\partial S}}={\frac {\partial ^{3}V}{\partial S^{3}}}}$

A esto también se lo denomina a veces gamma de gamma ^{[2] : 799} o DgammaDspot . ^[13] La velocidad es la tercera derivada de la función de valor con respecto al precio spot subyacente. Puede ser importante monitorear la velocidad cuando se cubre una cartera con cobertura delta o cobertura gamma.

Zoma

Zomma ^[4] mide la tasa de cambio de gamma con respecto a los cambios en la volatilidad.

${\displaystyle {\text{Zomma}}={\frac {\partial \Gamma }{\partial \sigma }}={\frac {\partial {\text{vanna}}}{\partial S}}={\frac {\partial ^{3}V}{\partial S^{2}\,\partial \sigma }}}$

Zomma también ha sido conocida como DgammaDvol . ^[13] Zomma es la tercera derivada del valor de la opción, dos veces del precio del activo subyacente y una vez de la volatilidad. Zomma puede ser una sensibilidad útil para monitorear cuando se mantiene una cartera con cobertura gamma, ya que ayudará al operador a anticipar cambios en la efectividad de la cobertura a medida que cambia la volatilidad.

Color

Color , ^[13] decaimiento gamma ^[19] o DgammaDtime ^[13] mide la tasa de cambio de gamma con el paso del tiempo.

${\displaystyle {\text{Color}}={\frac {\partial \Gamma }{\partial \tau }}={\frac {\partial ^{3}V}{\partial S^{2}\,\partial \tau }}}$

El color es una derivada de tercer orden del valor de la opción, dos veces con respecto al precio del activo subyacente y una vez con el tiempo. El color puede ser una sensibilidad importante a monitorear cuando se mantiene una cartera con cobertura gamma, ya que puede ayudar al operador a anticipar la efectividad de la cobertura a medida que pasa el tiempo.

El resultado matemático de la fórmula del color (ver más abajo) se expresa en gamma por año. A menudo resulta útil dividir esto por el número de días por año para llegar al cambio en gamma por día. Este uso es bastante preciso cuando el número de días que quedan hasta el vencimiento de la opción es grande. Cuando una opción se acerca al vencimiento, el color en sí puede cambiar rápidamente, lo que hace que las estimaciones del cambio de gamma para todo el día sean inexactas.

Última

Ultima ^[4] mide la sensibilidad de la opción vomma con respecto al cambio en la volatilidad.

${\displaystyle {\text{Ultima}}={\frac {\partial {\text{vomma}}}{\partial \sigma }}={\frac {\partial ^{3}V}{\partial \sigma ^{3}}}}$

Ultima también ha sido denominada DvommaDvol . ^[4] Ultima es una derivada de tercer orden del valor de la opción respecto de la volatilidad.

Los griegos apuestan por opciones multiactivos

Si el valor de un derivado depende de dos o más subyacentes , sus griegos se amplían para incluir los efectos cruzados entre los subyacentes.

El delta de correlación mide la sensibilidad del valor del derivado a un cambio en la correlación entre los subyacentes. ^[20] También se le conoce comúnmente como cega . ^{[21] [22]}

La gamma cruzada mide la tasa de cambio del delta en un subyacente ante un cambio en el nivel de otro subyacente. ^[23]

Cross vanna mide la tasa de cambio de vega en un subyacente debido a un cambio en el nivel de otro subyacente. De manera equivalente, mide la tasa de cambio del delta en el segundo subyacente debido a un cambio en la volatilidad del primer subyacente. ^[20]

Cross volga mide la tasa de cambio de vega en un subyacente ante un cambio en la volatilidad de otro subyacente. ^[23]

Fórmulas para la opción europea griega.

Los griegos de las opciones europeas ( calls y puts ) según el modelo de Black-Scholes se calculan de la siguiente manera, donde (phi) es la función de densidad de probabilidad normal estándar y es la función de distribución acumulativa normal estándar . Tenga en cuenta que las fórmulas gamma y vega son las mismas para opciones de compra y venta. ${\displaystyle \varphi }$ ${\displaystyle \Phi }$

Para una dada:

• Precio de mercado , ${\displaystyle S\,}$
• Precio de ejercicio , ${\displaystyle K\,}$
• Tasa libre de riesgo , ${\displaystyle r\,}$
• Rentabilidad anual por dividendo , ${\displaystyle q\,}$
• Tiempo hasta el vencimiento (representado como una fracción de un año sin unidades), y ${\displaystyle \tau =T-t\,}$
• Volatilidad . ${\displaystyle \sigma \,}$

dónde

${\displaystyle {\begin{aligned}d_{1}&={\frac {\ln(S/K)+\left(r-q+{\frac {1}{2}}\sigma ^{2}\right)\tau }{\sigma {\sqrt {\tau }}}}\\d_{2}&={\frac {\ln(S/K)+\left(r-q-{\frac {1}{2}}\sigma ^{2}\right)\tau }{\sigma {\sqrt {\tau }}}}=d_{1}-\sigma {\sqrt {\tau }}\\\varphi (x)&={\frac {1}{\sqrt {2\pi }}}e^{-{\frac {1}{2}}x^{2}}\\\Phi (x)&={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{x}e^{-{\frac {1}{2}}y^{2}}\,dy=1-{\frac {1}{\sqrt {2\pi }}}\int _{x}^{\infty }e^{-{\frac {1}{2}}y^{2}}\,dy\end{aligned}}}$

Según el modelo negro (comúnmente utilizado para materias primas y opciones sobre futuros), los griegos se pueden calcular de la siguiente manera:

dónde

${\displaystyle {\begin{aligned}d_{1}&={\frac {\ln(F/K)+{\frac {1}{2}}\sigma ^{2}\tau }{\sigma {\sqrt {\tau }}}}\\d_{2}&={\frac {\ln(F/K)-{\frac {1}{2}}\sigma ^{2}\tau }{\sigma {\sqrt {\tau }}}}=d_{1}-\sigma {\sqrt {\tau }}\end{aligned}}}$

(*) Se puede demostrar que ${\displaystyle F\varphi (d_{1})=K\varphi (d_{2})}$

Microprueba:

dejar ${\displaystyle x=\sigma {\sqrt {\tau }}}$

${\displaystyle d_{1}={\frac {\ln {\frac {F}{K}}+{\frac {1}{2}}x^{2}}{x}}}$

${\displaystyle d_{1}\cdot x=\ln {\frac {F}{K}}+{\frac {1}{2}}x^{2}}$

${\displaystyle \ln(F/K)=d_{1}\cdot x-{\frac {1}{2}}x^{2}}$

${\displaystyle {\frac {F}{K}}=e^{d_{1}\cdot x-{\frac {1}{2}}x^{2}}}$

Entonces nosotros tenemos: ${\displaystyle {\frac {F}{K}}\cdot {\frac {\varphi (d_{1})}{\varphi (d_{2})}}={\frac {F}{K}}\cdot e^{{\frac {1}{2}}\cdot {d_{2}}^{2}-{\frac {1}{2}}\cdot {d_{1}}^{2}}}$

${\displaystyle =e^{d_{1}x-{\frac {1}{2}}x^{2}}\cdot e^{{\frac {1}{2}}\cdot {(d_{1}-x)}^{2}-{\frac {1}{2}}\cdot {d_{1}}^{2}}=e^{d_{1}x-{\frac {1}{2}}x^{2}+{\frac {1}{2}}\cdot (2d_{1}-x)(-x)}=e^{0}=1.}$

Entonces ${\displaystyle F\varphi (d_{1})=K\varphi (d_{2})}$

Medidas relacionadas

A continuación se enumeran algunas medidas de riesgo relacionadas de los instrumentos financieros .

Duración del bono y convexidad.

En la negociación de bonos y otros valores de renta fija , se utilizan varias medidas de la duración de los bonos de manera análoga al delta de una opción. El análogo más cercano al delta es DV01 , que es la reducción del precio (en unidades monetarias) por un aumento de un punto básico (es decir, 0,01% anual) en el rendimiento (el rendimiento es la variable subyacente). Véase también Duración del bono § Riesgo: duración como sensibilidad a la tasa de interés .

Análoga a la lambda es la duración modificada , que es el cambio porcentual en el precio de mercado de los bonos por un cambio unitario en el rendimiento (es decir, equivale a DV01 dividido por el precio de mercado). A diferencia de la lambda, que es una elasticidad (un cambio porcentual en la producción por un cambio porcentual en los insumos), la duración modificada es en cambio una semielasticidad : un cambio porcentual en la producción por un cambio unitario en los insumos. Consulte también Duración de la tasa clave .

La convexidad del bono es una medida de la sensibilidad de la duración a los cambios en las tasas de interés , la segunda derivada del precio del bono con respecto a las tasas de interés (la duración es la primera derivada); entonces es análogo a gamma. En general, cuanto mayor es la convexidad, más sensible es el precio del bono a los cambios en las tasas de interés. La convexidad de los bonos es una de las formas de convexidad más básicas y más utilizadas en las finanzas .

Para un bono con una opción incorporada , los cálculos estándar basados ​​en el rendimiento al vencimiento aquí no consideran cómo los cambios en las tasas de interés alterarán los flujos de efectivo debido al ejercicio de la opción. Para abordar esto, se introducen la duración efectiva y la convexidad efectiva . Estos valores generalmente se calculan utilizando un modelo basado en árbol, construido para toda la curva de rendimiento (a diferencia de un único rendimiento al vencimiento) y, por lo tanto, captura el comportamiento de ejercicio en cada punto de la vida de la opción como una función tanto del tiempo como de las tasas de interés. ; ver Modelo de celosía (finanzas) § Derivados de tipos de interés .

Beta

La beta (β) de una acción o cartera es un número que describe la volatilidad de un activo en relación con la volatilidad del índice de referencia con el que se compara dicho activo. Este punto de referencia es generalmente el mercado financiero general y a menudo se estima mediante el uso de índices representativos , como el S&P 500 .

Un activo tiene una Beta de cero si sus rendimientos cambian independientemente de los cambios en los rendimientos del mercado. Una beta positiva significa que los rendimientos del activo generalmente siguen los rendimientos del mercado, en el sentido de que ambos tienden a estar por encima de sus respectivos promedios juntos, o ambos tienden a estar por debajo de sus respectivos promedios juntos. Una beta negativa significa que los rendimientos del activo generalmente se mueven en sentido opuesto a los rendimientos del mercado: uno tenderá a estar por encima de su promedio cuando el otro esté por debajo de su promedio.

Fugit

El fugitivo es el momento esperado para ejercer una opción estadounidense o bermuda. El fugit se calcula útilmente con fines de cobertura; por ejemplo, se pueden representar los flujos de un swap estadounidense como los flujos de un swap que comienzan en el fugit multiplicado por delta, y luego usarlos para calcular otras sensibilidades.

Ver también

• Alfa (finanzas)
• Beta (finanzas)
• Delta neutral
• Gestion de riesgos financieros
• Letras griegas utilizadas en matemáticas, ciencias e ingeniería.
• PnL explicado § Método de sensibilidades
• Precios de Vanna-Volga

Referencias

1. Bancos, Erik; Siegel, Paul (2006). El manual de aplicaciones de opciones: técnicas de cobertura y especulación para inversores profesionales . Profesional de McGraw-Hill . pag. 263.ISBN​ 9780071453158.
2. Macmillan, Lawrence G. (1993). Opciones como inversión estratégica (3ª ed.). Instituto de Finanzas de Nueva York . ISBN 978-0-13-636002-5.
3. Chriss, Neil (1996). Black-Scholes y más allá: modelos de valoración de opciones. Profesional de McGraw-Hill . pag. 308.ISBN​ 9780786310258.
4. Haug, Espen Gaardner (2007). La guía completa de fórmulas de fijación de precios de opciones . Profesional de McGraw-Hill . ISBN 9780071389976.
5. Suma, Juan. "Opciones griegas: riesgo y recompensa delta" . Consultado el 7 de enero de 2010 .
6. Steiner, Bob (2013). Dominar los cálculos financieros (3ª ed.). Pearson Reino Unido. ISBN 9780273750604.
7. Casco, John C. (1993). Opciones, futuros y otros valores derivados (2ª ed.). Prentice Hall . ISBN 9780136390145.
8. Omega - Investopedia
9. De Spiegeleer, enero; Schoutens, Wim (2015). El manual de bonos convertibles: fijación de precios, estrategias y gestión de riesgos . John Wiley e hijos . págs. 255, 269–270. ISBN 9780470689684.
10. Soklakov, AN (2023). "Geometría de la Información de Riesgos y Rentabilidades". Riesgo . Junio ​​. arXiv : 2206.08753 . SSRN  4134885.
11. Willette, Jeff (28 de mayo de 2014). "Comprender cómo la gamma afecta a Delta". www.traderbrains.com . Consultado el 7 de marzo de 2014 .
12. Willette, Jeff (28 de mayo de 2014). "¿Por qué la opción larga gamma es positiva?". www.traderbrains.com . Consultado el 7 de marzo de 2014 .
13. Haug, Espen Gaarder (2003), "Conozca su arma, parte 1" (PDF) , Revista Wilmott (mayo de 2003): 49–57, doi :10.1002/wilm.42820030313 (inactivo 2024-03-19){{citation}}: CS1 maint: DOI inactive as of March 2024 (link)
14. Derivados - Delta Decay - The Financial Encyclopedia
15. Haug, Espen Gaarder (2003), "Conoce tu arma, parte 2", Revista Wilmott (julio de 2003): 43–57
16. Pierino Ursone. Cómo calcular los precios de las opciones y sus griegos: exploración del modelo Black Scholes de Delta a Vega . John Wiley e hijos. 2015.
17. Derivados - Griegos de segundo orden - The Financial Encyclopedia
18. Breeden, Litzenberger, Precios de derechos contingentes al Estado implícitos en los precios de las opciones [1]
19. "Derivados - Griegos". Inversiones y finanzas . Consultado el 21 de diciembre de 2020 .
20. "Griegos para opciones de activos múltiples" . Consultado el 24 de enero de 2017 .
21. Riesgo de correlación . Consultado el 22 de marzo de 2018 .
22. "Opciones, valoración y riesgos de la Cordillera Rotativa / Análisis de desempeño" . Consultado el 22 de marzo de 2018 .
23. Fengler, Matías; Schwendner, Peter (2003). "Premia de riesgo de correlación para opciones de renta variable de activos múltiples" (PDF) . Humboldt-Universität zu Berlin, Wirtschaftswissenschaftliche Fakultät. doi :10.18452/3572. {{cite journal}}: Citar diario requiere |journal=( ayuda )

enlaces externos

Teoría

• Delta, Gamma, GammaP, Simetría gamma, Vanna, Velocidad, Charm, Saddle Gamma: Opciones vainilla - Espen Haug,
• Volga, Vanna, Speed, Charm, Color: Opciones de vainilla - Uwe Wystup, Opciones de vainilla - Uwe Wystup

Herramientas en línea

• griegos: Sensibilidades de los precios de las opciones financieras, paquete R para calcular griegos para opciones europeas, americanas y asiáticas