Mariposa (opciones)

Estrategia de negociación de opciones

Tabla de ganancias por comprar un spread mariposa.

Ganancias a partir de una posición de spread mariposa larga. El spread se crea comprando una opción call con un precio de ejercicio relativamente bajo (x ₁ ), comprando una opción call con un precio de ejercicio relativamente alto (x ₃ ) y vendiendo en corto dos opciones call con un precio de ejercicio intermedio (x ₂ ).

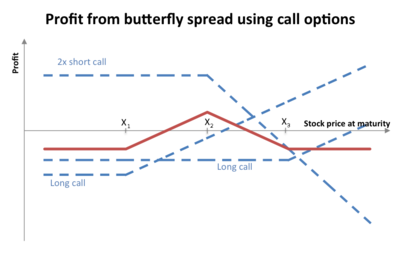
En finanzas , una mariposa (o simplemente una mosca ) es una estrategia de opciones no direccional y de riesgo limitado que está diseñada para tener una alta probabilidad de obtener una ganancia limitada cuando se espera que la volatilidad futura del activo subyacente sea menor (cuando se compra la mariposa) o mayor (cuando se vende la mariposa) que la volatilidad implícita actual de ese activo .

Mariposa larga

Una posición mariposa larga generará ganancias si la volatilidad futura es menor que la volatilidad implícita.

Una estrategia de opciones mariposa larga consta de las siguientes opciones :

• Opción larga de compra con un precio de ejercicio de (X − a)
• Posición corta de 2 opciones de compra con un precio de ejercicio de X
• Opción larga de compra con un precio de ejercicio de (X + a)

donde X = el precio al contado (es decir, el precio de mercado actual del activo subyacente) y a > 0.

Utilizando la paridad put-call también se puede crear una mariposa larga de la siguiente manera:

• Opción larga de venta con un precio de ejercicio de (X + a)
• Venta corta de 2 opciones put con un precio de ejercicio de X
• Opción de venta larga con un precio de ejercicio de (X − a)

donde X = precio spot y a > 0.

Todas las opciones tienen la misma fecha de vencimiento .

Al vencimiento el valor (pero no el beneficio) de la mariposa será:

• cero si el precio del activo subyacente es inferior a (X − a) o superior a (X + a)
• positivo si el precio del subyacente está entre (X - a) y (X + a)

El valor máximo se produce en X (ver diagrama).

Mariposa corta

Una posición corta de mariposa generará ganancias si la volatilidad futura es mayor que la volatilidad implícita.

Una estrategia de opciones mariposa corta consiste en las mismas opciones que una mariposa larga. Sin embargo, ahora la posición de opción de precio de ejercicio medio es una posición larga y las posiciones de opción de precio de ejercicio superior e inferior son cortas.

Requisitos de margen

En Estados Unidos, los requisitos de margen para todas las posiciones con opciones, incluidas las de tipo mariposa, se rigen por lo que se conoce como Regulación T. Sin embargo, a los corredores se les permite aplicar requisitos de margen más estrictos que las regulaciones.

Uso en el cálculo de distribuciones implícitas

El precio de un activo mariposa centrado en torno a un precio de ejercicio determinado puede utilizarse para estimar la probabilidad implícita de que el activo subyacente se encuentre a ese precio de ejercicio al vencimiento. Esto significa que el conjunto de precios de mercado de los activos mariposa centrados en torno a distintos precios de ejercicio puede utilizarse para inferir la creencia del mercado sobre la distribución de probabilidad del precio del activo subyacente al vencimiento. Esta distribución implícita puede ser diferente de la distribución lognormal asumida en el popular modelo de Black-Scholes , y estudiarla puede revelar formas en las que los activos del mundo real difieren de los activos idealizados descritos por Black-Scholes. ^[1]

Variaciones de la mariposa

1. La posición de doble opción en el medio se llama cuerpo, mientras que las otras dos posiciones se llaman alas.
2. En caso de que la distancia entre el precio de ejercicio medio y los ejercicios superiores e inferiores sea desigual, dicha posición se denomina mariposa de "alas rotas" (o "mosca rota" para abreviar).
3. Una mariposa de hierro recrea el diagrama de pagos de una mariposa, pero con una combinación de dos opciones de compra y dos de venta.
4. La estrategia de opción en la que las opciones intermedias (el cuerpo) tienen diferentes precios de ejercicio se conoce como Cóndor .
5. Una mariposa de árbol de Navidad (que no debe confundirse con la combinación de opciones no relacionadas también llamada árbol de Navidad ) consta de seis opciones que se utilizan para crear un diagrama de pagos similar a una mariposa pero ligeramente bajista o alcista en lugar de direccionalmente neutral. ^{[2] [3]}

Referencias

1. Natenberg, Sheldon (2015). "Capítulo 24". Volatilidad y fijación de precios de opciones: estrategias y técnicas de negociación avanzadas (segunda edición). Nueva York. ISBN 9780071818780.{{cite book}}: Mantenimiento de CS1: falta la ubicación del editor ( enlace )
2. "Llamado de mariposa del árbol de Navidad". www.optionsplaybook.com . Consultado el 19 de marzo de 2022 .
3. "Árbol de Navidad Mariposa puesta" www.optionsplaybook.com . Consultado el 19 de marzo de 2022 .

• McMillan, Lawrence G. (2002). Las opciones como inversión estratégica (4.ª ed.). Nueva York: New York Institute of Finance. ISBN 0-7352-0197-8.
• Crédito por parte de corredores y distribuidores (Reglamento T), FINRA, 1986